この解説は、公式解説と比べて本質的に新しい解法を示すものではありません。 が、後に AC に挑む方の助けになると思ったことをいくつか補足しておきます。

---

[1] 分離の判定について（一般論）

公式解説の 2 色のマスを作る方法はかなりトリッキーに思われるかもしれませんが、単純閉曲線（自己交差のない閉曲線）の次の性質によっていると考えることができます：

\(C\) を平面上の単純閉曲線とする。このとき、平面は \(C\) の内外の \(2\) 領域に分割される（Jordan 閉曲線定理）。さらに、平面上の \(C\) 上ではない点 \(p\) および、\(p\) を始点とする半直線 \(l\) を任意にとるとき、次が成り立つ：

• \(l\) と \(C\) の交差回数が偶数回ならば \(p\) は \(C\) の外側、奇数回ならば \(p\) は \(C\) の内側である。

次の 3 枚目の画像の示す通り、交差回数の定義は交点の個数を数えるだけでは不十分で、定式化はすこし大変なのですが、ここでは省略します。

この性質を使って、\(S\), \(G\) が \(C\) の内外どちら側にあるかを判定し、それが不一致となるかどうかにより分離が判定できます。

（単純閉曲線のこの性質は、https://atcoder.jp/contests/abc211/tasks/abc211_f などでも用いられていました）

---

[2] 分離の判定について（グリッド）

半直線をひとつずつ固定して交差を数えることで、各々の内外判定ができます。私は左図のように 2 本の半直線を考えて実装しました。解説のように 2 色のマス目を作ることに言い換えると、右図の形になるのかなと思います。

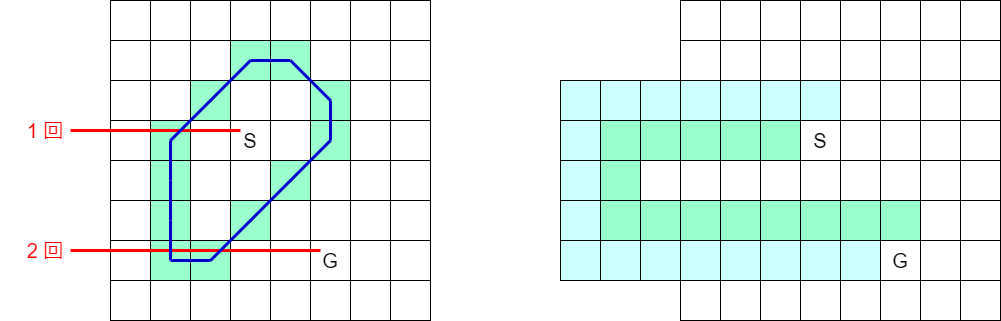
\(S\), \(G\) の2 マスの位置関係に全く依存せず、個々のマスごとに独立に交差回数を調べればよくなるので、公式解説と比べていくらか考えやすくなるかもしれません。

---

[3] コーナーケースについて

これがコーナーケースとなるかは実装依存かもしれませんが、個人的に苦労したので書いておきます（ところで本問題が本番中の AC が少なく高難易度という評価を受けているのは、解法の発想難易度の高さというよりも、細かいコーナーケースへの詰めを短時間でやりきる難易度の高さがかなり影響しているように思います）。

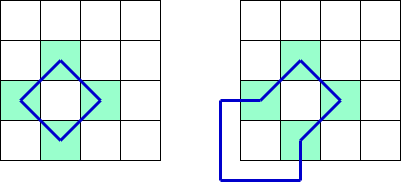
サイクルによる分離と見なせるパターン、パス（外壁と合わせたサイクル）による分離と見なせるパターンに分けて数える場合、マスの集合を見ても、どちらになるかが定まらない場合があります。これらを重複して数えないように注意が必要です。

要するに、 \(8\) 近傍の関係にある壁際の \(2\) マスをともに含むパス / サイクルが注意点です。

---

この場合について、単に片方のみを考えるようにすれば良いのかというと、そうでもありません。

実際、上左図と、上右図で、内部と判定している白マスの集合が異なるため、どちらかの見方だけでは内外判定が正しく行えない可能性があると分かります。

私はどちらとも考えられるマスの集合はサイクルと見なすことにしたのですが、次のようなコーナーケースのために、\(2\times n\) の場合の専用実装を追加する羽目になりました。

最小マス数でも、サイクルとして見ると分離できておらず、パス＋壁と見ると分離できているというパターンがありえます。どちらとも見なせるものはパスと見なすことにしておくと大丈夫だったかもしれません。

サンプルが合っても AC にならない場合、小さい盤面での愚直解（\(O(2^{HW}HW)\)時間かけるものなど）を書いてランダムチェックすることを検討してもよいと思います。