E - Filters Editorial by en_translator
A \(\Theta(NQ)\)-time solution of applying \(f_1, f_2, \dots, f_N\) to each of \(x_1, x_2, \dots, x_Q\) will lead to TLE, because \(NQ\) can be up to \(4 \times 10^{10}\).
Now let us consider how the composite function \(F(x) = f_N(\dots f_2(f_1(x))\dots)\) looks like.
When \(t_i = 1\), \(f_i\) is an operation of shifting the graph vertically;
when \(t_i = 2\), \(f_i\) is an operation of clamping the graph to at least \(a_i\);
when \(t_i = 3\), \(f_i\) is an operation of clamping the graph to at most \(a_i\).
Thus, we can expect that the composition of those operations forms like the graph below — namely, there exist numbers \(a, b, c\) such that \(F(x) = \min(c, \max(b, x + a))\).
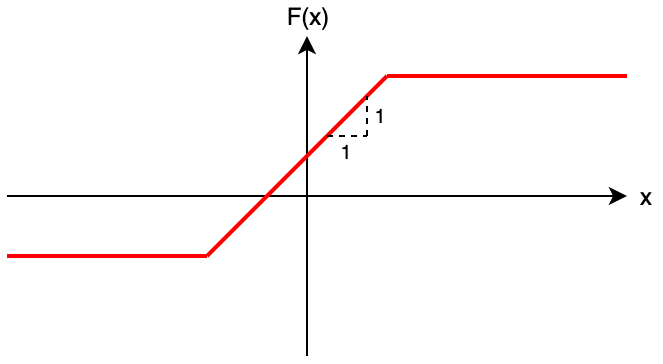
We can prove the fact in the following way:
When \(t_i = 1\), \(f_i(x) = \min(\infty, \max(-\infty, x + a_i))\);
when \(t_i = 2\), \(f_i(x) = \min(\infty, \max(a_i, x + 0))\);
when \(t_i = 3\), \(f_i(x) = \min(a_i, \max(-\infty, x + 0))\); so we can always express \(f_i\) in the form of \(\min(c, \max(b, x + a))\).
Also, let \(f(x) = \min(c_1, \max(b_1, x + a_1)), g(x) = \min(c_2, \max(b_2, x + a_2))\); then their composite function \(g(f(x))\) satisfies
\[ \begin{aligned} g(f(x)) &= \min(c_2, \max(b_2, \min(c_1, \max(b_1, x + a_1)) + a_2))\\ &= \min(c_2, \max(b_2, \min(c_1 + a_2, \max(b_1 + a_2, x + a_1 + a_2))))\\ &= \min(\min(c_2, \max(b_2, c_1 + a_2)), \max(\max(b_2, \min(c_1 + a_2, b_1 + a_2)), x + (a_1 + a_2))),\\ \end{aligned} \]
so it can be represented as \(\min(c, \max(b, x + a))\).
Since \(F(x)\) are the composition of \(f_1, f_2, …, f_N\), it is proved that be represented in the form of \(\min(c, \max(b, x + a))\).
Next, let us find \(a, b, c\) when it is expressed as \(F(x) = \min(c, \max(b, x + a))\).
These can be calculated by compositing based on the composition rule \(g(f(x)) = \min(\min(c_2, \max(b_2, c_1 + a_2)), \max(\max(b_2, \min(c_1 + a_2, b_1 + a_2)), x + (a_1 + a_2)))\) described above.
Once we have \(a, b,\) and \(c\), we can calculate \(F(x)\) in \(O(1)\) time each, so the problem has been solved in a total of \(O(N + Q)\) time.
Sample Code (C++)
#include <iostream>
#include <numeric>
#include <algorithm>
using namespace std;
using ll = long long;
const ll INF = numeric_limits<ll>::max() / 4;
void chmin(ll& a, ll b){ if(a > b) a = b; }
void chmax(ll& a, ll b){ if(a < b) a = b; }
int main(){
ll N;
cin >> N;
ll low = -INF, high = INF, add = 0;
for(ll i = 0; i < N; i++){
ll A, T;
cin >> A >> T;
if(T == 1){
low += A;
high += A;
add += A;
}
else if(T == 2){
chmax(low, A);
chmax(high, A);
}
else{
chmin(low, A);
chmin(high, A);
}
}
ll Q;
cin >> Q;
for(ll i = 0; i < Q; i++){
ll x;
cin >> x;
cout << clamp(x + add, low, high) << '\n';
}
}
Sample Code (Python)
N = int(input())
low = -1 << 60
high = 1 << 60
add = 0
for i in range(N):
A, T = map(int, input().split())
if T == 1:
low += A
high += A
add += A
elif T == 2:
if low < A:
low = A
if high < A:
high = A
else:
if low > A:
low = A
if high > A:
high = A
input()
for x in map(int, input().split()):
print(min(high, max(low, x + add)))
posted:
last update: