(Due to a bug, some subscripts are substituted by bracketed indices)

Let us focus on the conditions that \(1≤i<j≤N\).

When \(i\) is \(1\), \(j\) will move between \(2\) and \(N\), and when \(i\) is \(2\), \(j\) will move between \(3\) and \(N\). Generally, for each \(i\), \(j\) can be between \(i+1\) and \(N\).

Let us fix \(i\). The desired value is the sum of \(A_i × A_j\), that is,

\(A[i ]× A[i+1] + A[i] × A[i+2] + ... + A[i] × A[N].\)

Since there are \(N-i\) number of products, the time complexity of this naive calculation will be \(O(N)\).

By transforming the expression, one can obtain

\(A[i] × (A[i+1] + A[i+2] + .... + A[N]).\)

This expression still has \(N-i\) number of additions, so the time complexity of this calculation is \(O(N)\) too.

However, since \( (A[i+1] + A[i+2] + .... + A[N])\) is a continuous segment of sequence \(A\), this can be solved in an \(O(1)\) time with cumulative sums. If you do not know cumulative sums, search for “cumulative sum.”

Also, this can be solved without knowledge of cumulative sums. While iterating \(i\) one by one, the segement sum required will differs only by one element. For example, when \(i=1\), one needs

\(A[2] + A[3] + A[4] + ... + A[N],\)

while when \(i = 2\), one needs

\(A[3] + A[4] + ... + A[N],\)

and these differs only by \(A[2]\). By making use of this property, you can find the segment sum for each iteration by subtracting proper elements, thus solve this problem.

With this idea, the value for each \(i\) can be found in an \(O(1)\) time. so the total time complexity will be \(O(N)\), which is fast enough for the time constraiants to solve this problem.

If you are not good at transofrming equations, you may be able to imagine diagrams.

Take edges of length \(A_1, A_2, ... A_N\) vertically and horizontally, then you will obtain the following diagram.

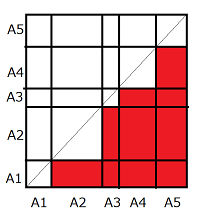
Think like this: for example, when \(i =2, j=3\), refer to the rectanlge of width \(A_2\) and height \(A_3\). Then one can see the total area of the parts painted red is the answer.

There are several ways of finding the area. Splitting this into \(N\) rectangles corresponds to the solution described above. You can also find the answer by calculating the area of the whole rectangle subtracted by the center \(N\) blocks. However, since you are asked to find the answer modulo \(10^9 + 7\), you cannot simply divide by two; instead, you have to use modular inverse, which is a difficult solution.

Sample Code(C++, Find segments sums with cumulative susm)

Sample Code(C++, Remove the center blocks and halve)

Sample Code(C++, Calculate segements sums using differences)

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int N;
	cin >> N;
	vector<int> A(N);
	int mod = 1000000007;
	long long sum = 0;
	for (int i = 0; i < N; i++)
	{
		cin >> A[i];
		sum += A[i];
		sum %= mod;
	}

	long ans = 0;

	//Search for all i
	for (int i = 0; i < N; i++)
	{
		//Update the values of A[i+1] ... A[N]
		sum -= A[i];
		if (sum < 0) sum += mod;

		ans += A[i] * sum;
		ans %= mod;
	}

	cout << ans << endl;
}