(不具合により、一部下付き文字を添え字に変更しています)

\(1≤i<j≤N\)という条件に注目してみましょう。

\(i\) が\(1\) の時、\(j\) は \(2\) から \(N\) の値を。\(i\) が\(2\) の時、\(j\) は \(3\) から \(N\) の値を取ります。\(i\) に対して、\(j\) が取れる値は、\(i+1\) から \(N\) となるわけです。

ここで、\(i\) を固定して考えてみましょう。求める値は、\(A_i × A_j\) の和なので、

\(A[i ]× A[i+1] + A[i] × A[i+2] + ... + A[i] × A[N]\)

となります。掛け算回数は \(N-i\) 回あるため、このままだと計算量は\(O(N)\) となります。

これを式変形すると、

\(A[i] × (A[i+1] + A[i+2] + .... + A[N])\)

となります。この場合でも、足し算が \(N-i\) 回続くため、このままだと計算量は\(O(N)\) となります。

ですが、\( (A[i+1] + A[i+2] + .... + A[N])\)が、数列 \(A\) に対する連続区間であることを考えると、累積和を予め求めておけば、 \(O(1)\) で解くことが出来ます。累積和を知らない場合は、「累積和」で検索してみましょう。

また、累積和を知らなくても解く方法はあります。\(i\) を \(1\) から順番に試していくのであれば、必要となる区間和は、\(1\) つ分しか変わりません。例えば \(i = 1\) のときは

\(A[2] + A[3] + A[4] + ... + A[N]\)

が必要となりますが、\(i = 2\) の時は

\(A[3] + A[4] + ... + A[N]\)

が必要となり、これは \(A[2]\) の違いしかありません。これを活用して、毎回この引き算で必要な区間和を求めることで、この問題を解くことが出来ます。

この考え方を使うと、各 \(i\) についての値が \(O(1)\) で求められるため、全ての \(i\) について順番に計算しても、計算時間は\(O(N)\) となり、制限時間内に問題を解くことが出来ます。

なお、式変形が苦手な場合は、図形をイメージすることで解くことが出来るかも知れません。

縦横に長さ \(A_1, A_2, ... A_N\) を取ると、以下のような図を作成することが出来ます。

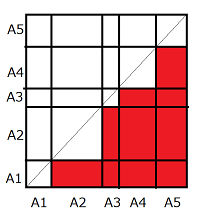
例えば、\(i =2, j=3\) のときは、縦が\(A_2\) , 縦が \(A_3\) となる長方形を参照する、のように考えると、赤く塗った部分の面積が求める答えになります。

この面積の求め方は複数ありますが、\(N\) 個の長方形に分割するのが、前述した解き方と対応します。それ以外にも、中央の\(N\) 個のブロックを除いた面積の半分、といった解き方をすることも可能です。ただし、今回求める値は10億7で割ったあまりなので、単純で \(2\) で割ることが出来ないため、逆元を使う難しい解法になってしまうことに気をつけてましょう。

回答例(C++, 累積和を用いて区間和を計算する)

回答例(C++, 真ん中のブロックを取り除いて半分にする)

回答例(C++, 差分を用いて区間和を計算する)

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int N;
	cin >> N;
	vector<int> A(N);
	int mod = 1000000007;
	long long sum = 0;
	for (int i = 0; i < N; i++)
	{
		cin >> A[i];
		sum += A[i];
		sum %= mod;
	}

	long ans = 0;

	//i について全探索する
	for (int i = 0; i < N; i++)
	{
		//A[i+1] ... A[N] の値を更新する
		sum -= A[i];
		if (sum < 0) sum += mod;

		ans += A[i] * sum;
		ans %= mod;
	}

	cout << ans << endl;
}