C - Bridge

Contest Duration: 2017-10-14(Sat) 12:00 - 2017-10-14(Sat) 13:40 (local time) (100 minutes) Back to Home

C - Bridge Editorial

Time Limit: 2 sec / Memory Limit: 256 MB

配点 : $300$ 点

問題文

自己ループと二重辺を含まない $N$ 頂点 $M$ 辺の無向連結グラフが与えられます。
$i(1≦i≦M)$ 番目の辺は頂点 $a_i$ と頂点 $b_i$ を結びます。

グラフから辺を取り除いたとき、グラフ全体が非連結になるような辺のことを橋と呼びます。
与えられた $M$ 本のうち橋である辺の本数を求めてください。

ノート

自己ループ とは、 $a_i=b_i(1≦i≦M)$ であるような辺 $i$ のことをいいます。
二重辺 とは、 $a_i=a_j$ かつ $b_i=b_j(1≦i<j≦M)$ であるような辺の組 $i,j$ のことをいいます。
無向グラフが連結であるとは、グラフの任意の二頂点間に経路が存在することをいいます。

制約

$2≦N≦50$
$N-1≦M≦min(N(N−1)⁄2,50)$
$1≦a_i<b_i≦N$
与えられるグラフは自己ループと二重辺を含まない。
与えられるグラフは連結である。

入力

入力は以下の形式で標準入力から与えられる。

 $N$   $M$   
 $a_1$   $b_1$   
 $a_2$   $b_2$ 
 $:$   
 $a_M$   $b_M$

出力

$M$ 本の辺のうち、橋である辺の本数を出力せよ。

入力例 1Copy

Copy

出力例 1Copy

Copy

与えられるグラフは以下の図で表されます。

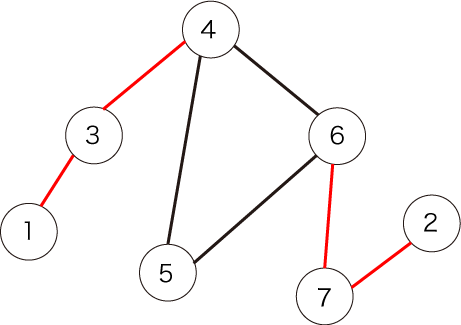
図の赤い辺が橋であり、その数は $4$ 本です。

入力例 2Copy

Copy

出力例 2Copy

Copy

橋である辺が存在しない場合もあります。

入力例 3Copy

Copy

出力例 3Copy

Copy

全ての辺が橋である場合もあります。

Score : $300$ points

Problem Statement

You are given an undirected connected graph with $N$ vertices and $M$ edges that does not contain self-loops and double edges.
The $i$ -th edge $(1 \leq i \leq M)$ connects Vertex $a_i$ and Vertex $b_i$ .

An edge whose removal disconnects the graph is called a bridge.
Find the number of the edges that are bridges among the $M$ edges.

Notes

A self-loop is an edge $i$ such that $a_i=b_i$ $(1 \leq i \leq M)$ .
Double edges are a pair of edges $i,j$ such that $a_i=a_j$ and $b_i=b_j$ $(1 \leq i<j \leq M)$ .
An undirected graph is said to be connected when there exists a path between every pair of vertices.

Constraints

$2 \leq N \leq 50$
$N-1 \leq M \leq min(N(N−1)⁄2,50)$
$1 \leq a_i<b_i \leq N$
The given graph does not contain self-loops and double edges.
The given graph is connected.

Input

Input is given from Standard Input in the following format:

 $N$   $M$   
 $a_1$   $b_1$   
 $a_2$   $b_2$ 
 $:$   
 $a_M$   $b_M$

Output

Print the number of the edges that are bridges among the $M$ edges.

Sample Input 1Copy

Copy

Sample Output 1Copy

Copy

The figure below shows the given graph:

The edges shown in red are bridges. There are four of them.

Sample Input 2Copy

Copy

Sample Output 2Copy

Copy

It is possible that there is no bridge.

Sample Input 3Copy

Copy

Sample Output 3Copy

Copy

It is possible that every edge is a bridge.