本質的には公式解説と同じです。

答えを二分探索します。以下、\(x>0\) を固定し、「\(x\) 以上となる組を最大何個作れるか」という問題を考えます。

最大マッチング

次のような二部グラフを考え、その最大マッチングのサイズを求めることを考えます。

• 頂点集合を \(\{X_1, \ldots,X_{2N},Y_1,\ldots,Y_{2N}\}\) とする。\(A_i\oplus A_j \geq x\) であるとき、かつそのときに限り \(X_i,Y_j\) 間に辺を張る

（この最大マッチング問題から元の問題の答えが得られることは後で示します）

以下、\(X_i\) の集合を「左側」、\(Y_i\) の集合を「右側」と呼ぶことにします。また、頂点と対応する数を同一視します。

このグラフは辺の数が \(O(N^2)\) になるので、グラフを陽に構築することは無理です。そこで上位 bit から再帰的に考えます。

\(x,A_i\) の中で最大の数の最上位 bit が \(k\) bit 目であるとし、\(k\) bit 目に注目します。
\(x\) の \(k\) bit 目が \(1\) のとき、「左側で \(k\) bit 目 が \(0\) のものと右側で \(k\) bit 目が \(1\) のもの」「左側で \(k\) bit 目が \(1\) のものと右側で \(k\) bit 目が \(0\) のもの」をそれぞれマッチングさせるしかありません。これの2つは明らかに独立な問題なのでそれぞれ再帰的に解きます。
\(x\) の\(k\) bit 目が \(0\) なら、まず再帰で「左側で \(k\) bit 目が \(0\) のものと右側で \(k\) bit 目が \(0\) のもの」「左側で \(k\) bit 目が \(1\) のものと右側で \(k\) bit 目が \(1\) のもの」の最大マッチングのサイズをそれぞれ再帰で求めておきます。そうして、左右それぞれ \(k\) bit 目が \(0\) か \(1\) かで \(2\) 頂点に圧縮して、「ソース+左 \(2\) 頂点+右 \(2\) 頂点+シンク」の \(6\) 頂点の最大流問題を解くことで、最大マッチングのサイズを求めることができます。適切に場合分けすることで、最大流問題用のアルゴリズムを使うことなく、いくつかのif文で解くことができます。

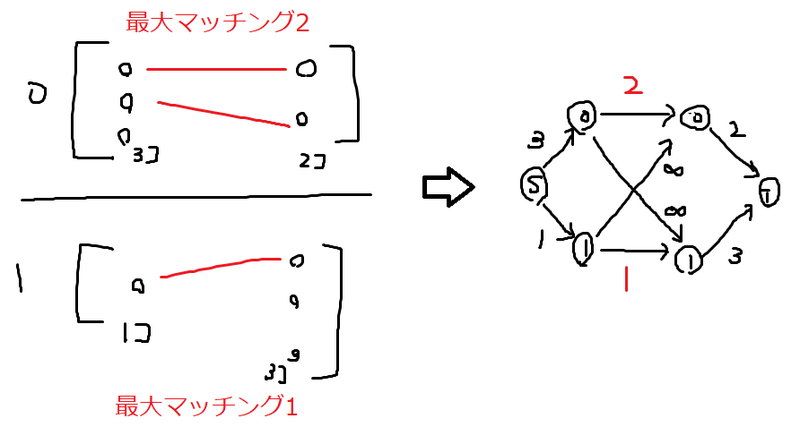
以上により問題が解けました。左右のどちらかが空集合になった次点で再帰をやめることで、計算量は \(O(N\log A)\) になります。

元の問題

上で求めた最大マッチングのサイズ÷2(切り捨て)が元の問題の解であることを示します。

頂点 \(Z_1,\ldots,Z_{2N}\) を用意し、求めたマッチングにおいて、\(X_i,Y_j\) 間に辺が存在するとき、かつそのときに限り \(Z_i,Z_j\) 間に辺を張ったグラフ \(G\) を考えます。\(G\) の全ての頂点の次数は \(2\) 以下なので、\(G\) はパスとサイクルからなります。\(G\) が辺数奇数の連結成分を高々 \(1\) つしかもたないとき、\(G\) の最大マッチングのサイズは \(G\) の辺数÷2(切り捨て)に等しくなります。よって、示すべきは \(G\) が辺数奇数の連結成分を高々 \(1\) つしかもたないことです。

\(x\) の最上位bitが \(1\) であるとき、「左側で最上位 bit が \(0\) のものと右側で最上位 bit が \(1\) のもの」「左側で最上位 bit が \(1\) のものと右側で最上位 bit が \(0\) のもの」の\(2\) つは本質的に等価であることから、対称なマッチングを作ることで、\(G\) はサイズ \(2\) のサイクルのみからなるようにできます。

そうでないときを考えます。\(A_i\) の中に 最上位 bit が \(0\) である数の方が多いとして良いです（\(A_i\) および \(x\) の最上位 bit を flip すればよい）。最初に0-1,1-0の辺に、同時に1ずつ流せるだけフローを流します。次に0-0辺に2ずつ流せるだけフローを流します。帰納法により、この時点で \(G\) は辺数奇数の連結成分を持たないようにできます。これ以上フローを流す方法は「0-0辺に1流す」「0-0辺を1つ戻して0-1,1-0辺に1ずつ流す」のどちらかです（1より多くは流せません）。前者は明らかに辺数奇数の連結成分がちょうど \(1\) つできます。後者は戻した0-0辺を含んでいた連結成分に辺が \(2\) つ増えるので、この連結成分の辺数が \(1\) 増え、辺数奇数の連結成分がちょうど \(1\) つできます。

以上で証明できました。