問題文

1 個の入力ファイルにつき T 個のテストケースが与えられる．各テストケースで次のようなグラフ G が与えられるので，以下の問に答えよ．

G は N 頂点 M 辺の無向単純グラフである．頂点には 1, 2, \ldots, N と番号が付いている．i 番目 (1 \le i \le M) の辺は頂点 A_i と頂点 B_i を結ぶ．

G の各頂点と各辺を金色と銀色のいずれかで塗る方法を考える (そのような塗り方は 2^{N+M} 通りある)．芸術的な塗り方とは，以下の条件をすべて満たす塗り方のこととする：

• 任意の金色の辺に対し，それが結ぶ頂点のうち少なくとも 1 つは金色である．
• 任意の銀色の頂点に対し，それに接続する辺のうち少なくとも 1 つは銀色である．

芸術的な塗り方の個数を 2 で割った余りを求めよ．

制約

• 1 \le T \le 100．
• 0 \le N \le 2024．
• 0 \le M \le 2024．
• 1 \le A_i < B_i \le N   (1 \le i \le M)．
• 1 \le i < j \le M のとき，(A_i, B_i) \ne (A_j, B_j)．

入力例 1

1
3 2
1 2
1 3

出力例 1

1

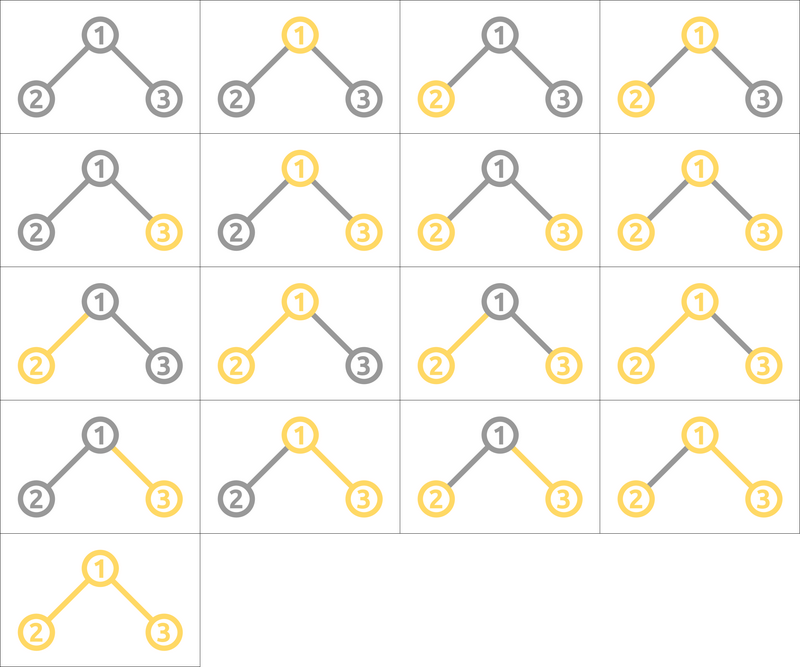
1 個目のテストケースでは，芸術的な塗り方は以下の図の 17 通りである．

問題文

値 0，二項演算 +，括弧 (, ) のみからなる数式を考える．正確には，本問において数式とは以下の BNF によって定義される <expression> とする：

<expression> ::= <term> | <expression> "+" <term>
<term> ::= "0" | "(" <expression> ")"

くろうさはある数式 s を隠し持っている．s の奇数文字目 (先頭を 1 文字目と数える) をすべて文字 _ で置き換えた文字列 T が与えられる．s としてあり得るものを 1 つ求めよ．

制約

• T は長さ 1 以上 10^6 以下の文字列である．
• ある数式 s が存在して，s の奇数文字目をすべて文字 _ で置き換えると T になる．

入力例 1

_0_0_

出力例 1

(0+0)

(0+0) が数式であることは次のようにわかる．

• 0 は <term> であるから，<expression> でもある．
• 0 は <expression> であり，0 は <term> であるから，0+0 は <expression> である．
• 0+0 は <expression> であるから，(0+0) は <term> であり，よって <expression> でもある．

入力例 2

_(_(_)_)_

出力例 2

((((0))))

問題文

正整数 M と，整数係数多項式 F(t) = \sum_{i=0}^{M-1} F_i t^i が与えられる．

また，K 個の正整数 N_0, N_1, \ldots, N_{K-1} と，K 元整数係数多項式 G(x_0, x_1, \ldots, x_{K-1}) = \displaystyle\sum_{j_0=0}^{N_0-1} \displaystyle\sum_{j_1=0}^{N_1-1} \cdots \displaystyle\sum_{j_{K-1}=0}^{N_{K-1}-1} G_j x_0^{j_0} x_1^{j_1} \cdots x_{K-1}^{j_{K-1}} が与えられる．ここで，和の内側において j = j_0 + N_0 j_1 + (N_0 N_1) j_2 + \cdots + (N_0 N_1 \cdots N_{K-2}) j_{K-1} である．

0 \le j_k < N_k を満たす各整数組 (j_0, j_1, \ldots, j_{K-1}) について，合成 F(G(x_0, x_1, \ldots, x_{K-1})) の x_0^{j_0} x_1^{j_1} \cdots x_{K-1}^{j_{K-1}} の係数を 998244353 で割った余りを求めよ．

制約

• 1 \le M \le 2^{16}．
• 0 \le F_i < 998244353   (0 \le i < M)．
• 1 \le K \le 16．
• 2 \le N_0 \le N_1 \le \cdots \le N_{K-1}．
• N_0 N_1 \cdots N_{K-1} \le 2^{16}．
• 0 \le G_j < 998244353   (0 \le j < N_0 N_1 \cdots N_{K-1})．

入力例 1

3
4 2000 1000000
2
2 3
3 2 6 4 5 1

出力例 1

9006004 12004000 36012000 48008000 66010000 74002000

F(t) = 4 + 2000 t + 1000000 t^2,\, G(x_0, x_1) = 3 + 2 x_0 + 6 x_1 + 4 x_0 x_1 + 5 x_1^2 + 1 x_0 x_1^2 である．

入力例 2

4
20 24 12 24
1
10
0 1 1 2 3 5 8 13 21 34

出力例 2

20 24 36 96 204 456 960 1992 4020 7968

入力例 3

15
2 3 6 11 23 47 106 235 551 1301 3159 7741 19320 48629 123867
3
3 3 3
1 1 2 3 5 7 11 15 22 30 42 56 77 101 135 176 231 297 385 490 627 792 1002 1255 1575 1958 2436

出力例 3

205001 2733669 22444763 8201007 115532895 978118598 182867184 683781124 283511483 82010070 135215245 487076637 271695954 473451928 217234716 349364028 711882268 472200539 360235417 248161311 666997398 886133207 465643853 863287257 136771343 714472215 407369010

問題文

正整数 m に対して，素数 p であって m が p^2 で割り切れるようなものの個数を f(m) とする．

正整数 N, A が与えられる．集合 \{ \lfloor N/i \rfloor \mid i \in \{1,2,\ldots,N\} \} の元が n_1 < n_2 < \cdots < n_k の k 個であるとする．

j = 1, 2, \ldots, k に対し，\displaystyle\sum_{m=1}^{n_j} f(m)^A を 998244353 で割った余りを g_j とおく．このとき，\displaystyle\sum_{j=1}^k 2024^j g_j を 10^9+7 で割った余りを求めよ．

制約

• 1 \le N \le 10^{14}．
• 1 \le A \le 10^{14}．

入力例 1

15 1

出力例 1

235928270

k = 6,\, (n_1, n_2, n_3, n_4, n_5, n_6) = (1, 2, 3, 5, 7, 15) であり，(g_1, g_2, g_3, g_4, g_5, g_6) = (0, 0, 0, 1, 1, 4) となる．

入力例 2

40 10

出力例 2

236425420

k = 11,\, (n_1, n_2, n_3, n_4, n_5, n_6, n_7, n_8, n_9, n_{10}, n_{11}) = (1, 2, 3, 4, 5, 6, 8, 10, 13, 20, 40) であり，(g_1, g_2, g_3, g_4, g_5, g_6, g_7, g_8, g_9, g_{10}, g_{11}) = (0, 0, 0, 1, 1, 1, 2, 3, 4, 7, 1037) となる．

入力例 3

123456 789

出力例 3

662299501

g_k = 498410667 となる．

入力例 4

100000000000000 100000000000000

出力例 4

913813068

N = 10^{14},\, A = 10^{14} である．

問題文

N 頂点の木が与えられる．頂点には 1, 2, \ldots, N と番号が付いている．i 番目 (1 \le i \le N - 1) の辺は頂点 A_i と頂点 B_i を結ぶ．

また，N \times N 個の非負整数 C(x,y) が与えられる (1 \le x, y \le N)．これは C(x,y) = C(y,x) を満たす．

(1, 2, \ldots, N) の順列 p = (p(1), p(2), \ldots, p(N)) に対し，p のコストを \displaystyle\sum_{i=1}^{N-1} C(p(A_i), p(B_i)) として定める．コストとしてあり得る最小値，および，コストを最小化する順列 p の個数を求めよ．

制約

• 1 \le N \le 18．
• 1 \le A_i < B_i \le N   (1 \le i \le N - 1)．
• A_i, B_i によって問題文中の木が定まる．
• 0 \le C(x,y) \le 10^7   (1 \le x, y \le N)．
• C(x,x) = 0   (1 \le x \le N)．
• C(x,y) = C(y,x)   (1 \le x, y \le N)．

入力例 1

5
1 2
1 3
2 4
2 5
0 7 9 5 7
7 0 9 9 6
9 9 0 5 9
5 9 5 0 9
7 6 9 9 0

出力例 1

24 2

コストの最小値は 24 であり，それを達成する p は (4, 1, 3, 2, 5) と (4, 1, 3, 5, 2) の 2 個である．

例えば p = (4, 1, 3, 2, 5) のとき，コストは C(4, 1) + C(4, 3) + C(1, 2) + C(1, 5) = 5 + 5 + 7 + 7 = 24 となる．

入力例 2

7
1 2
2 3
1 4
4 5
1 6
6 7
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 10000000
0 0 0 0 0 0 10000000
0 0 0 0 10000000 10000000 0

出力例 2

0 2448

問題文

非負整数 n, m に対し，n 頂点 m 辺のラベル付き単純二部グラフの個数を B(n, m) とする (ラベル付きとは，n 個の頂点が区別されるということ)．

非負整数 N と，A \in \mathbb{F}_{2^{64}} が与えられる．各 n = 0, 1, \ldots, N に対し，g_n = \displaystyle\sum _ {m\ge0} B(n, m) A^m を求めよ．

この問題の入出力では，\mathbb{F}_{2^{64}} の元を 0 以上 2^{64} 未満の nimber によって表す．すなわち g_n は，B(n, m) が奇数であるような m に対する，m 個の A の nim 積の，総 XOR である．

制約

• 0 \le N \le 10^6．
• A \in \mathbb{F}_{2^{64}}．

入力例 1

5 8

出力例 1

1 1 9 4 6 12

n \le 5 の範囲で B(n, m) が奇数であるのは (n, m) = (0, 0), (1, 0), (2, 0), (2, 1), (3, 0), (3, 1), (3, 2), (4, 0), (4, 2), (4, 4), (5, 0), (5, 2) のときであるから，

• g_0 = A^0
• g_1 = A^0
• g_2 = A^0 + A^1
• g_3 = A^0 + A^1 + A^2
• g_4 = A^0 + A^2 + A^4
• g_5 = A^0 + A^2

となる (これらは \mathbb{F}_{2^{64}} における演算であることに注意せよ)．

A^0, A^1, A^2, A^3, A^4 を表す nimber は，それぞれ 1, 8, 13, 14, 10 となる．

入力例 2

16 18446744073709551615

出力例 2

1 1 18446744073709551614 7156334549604198409 5893837254661243073 11290409524105353206 1851073793877042652 6387559487065781530 10238440391911562788 4437985372483032842 7848075886096899333 1584478287860827173 12600881811381958477 3270981160664397218 17529507309351360274 100266085651560874 1725589564589995945

問題文

くろうさとしろうさがとあるゲームで対戦する．このゲームの状態は，「いくつかの皿が並んでいて，各皿の上にいくつかのキャンディが置かれている」という状況で表される．

このゲームは，与えられる整数 A \in \{0,1,2,3,4\},\, B \in \{0,1,2\},\, C \in \{0,1\},\, D \in \{0,1\} によって，以下のルールが指定される．詳細はそれぞれ後述される．

• A は操作を定める．操作とは，ある 1 枚の皿に対してそれを変化させることである．
• B は行動を定める．行動は，いくつかの操作を同時にすることを指す．くろうさが先手・しろうさが後手で，くろうさとしろうさは交互に行動をする．
• C は終了を定める．ゲームが終了する条件を表す．
• D は勝敗を定める．ゲームが終了したときくろうさとしろうさの一方が勝ちとなり他方が負けとなる．

このゲームの初期状態が T 個指定される．各初期状態は，皿の枚数 N と各皿に置かれているキャンディの個数 X_1, X_2, \ldots, X_N によって与えられる．各初期状態について独立に，くろうさとしろうさのどちらに必勝法があるか判定せよ．

操作

キャンディが x 個置かれている皿に対する操作を以下で定める．いずれの場合も，皿に置かれているより多くのキャンディを取ることはできない．また，食べたキャンディはなくなる．

• A = 0 のとき，1 個以上のキャンディを取って食べる．
• A = 1 のとき，1 個以上 3 個以下のキャンディを取って食べる．
• A = 2 のとき，1 個以上 \left\lfloor \dfrac{1}{2} x \right\rfloor 個以下のキャンディを取って食べる．
• A = 3 のとき，
  • x が 17 の倍数であるとき，ちょうど 1 個のキャンディを取って食べる．
  • x が 17 の倍数でないとき，1 個以上 2 個以下のキャンディを取って食べる．
• A = 4 のとき，1 個以上 x-1 個以下のキャンディを取り，新しい皿を 1 枚用意してそこに置く (皿の枚数が増える)．

行動

行動を以下で定める．

• B = 0 のとき，ちょうど 1 枚の皿を選んで，操作をする (可能な操作が存在しない皿は選べない)．
• B = 1 のとき，1 枚以上の皿を選んで，それぞれに対して操作をする (可能な操作が存在しない皿は選べない)．
• B = 2 のとき，可能な操作が存在するような皿をすべて選んで，それぞれに対して操作をする (可能な操作が存在しない皿は無視する)．

終了

ゲームが終了する条件を以下で定める．

• C = 0 のとき，すべての皿に対して，可能な操作が存在しないとき，ゲームを終了する．
• C = 1 のとき，ある皿に対して，可能な操作が存在しないとき，ゲームを終了する．

勝敗

ゲームが終了したとき，次の手番が誰か (次に行動するはずだったのは誰か) によって，勝敗の判定を以下で定める．

• D = 0 のとき，次の手番の方が負けとなり，他方が勝ちとなる．
• D = 1 のとき，次の手番の方が勝ちとなり，他方が負けとなる．

制約

• A \in \{0,1,2,3,4\}．
• B \in \{0,1,2\}．
• C \in \{0,1\}．
• D \in \{0,1\}．
• 1 \le T \le 10^4．
• 各初期状態について，1 \le N \le 50．
• 各初期状態について，1 \le X_i \le 5 \times 10^5   (1 \le i \le N)．

部分点

• a \in \{0,1,2,3,4\},\, b \in \{0,1,2\},\, c \in \{0,1\},\, d \in \{0,1\} を満たす各組 (a, b, c, d) に対し，(A, B, C, D) = (a, b, c, d) を満たすデータセットに正解した場合は，それぞれ d + 1 点が与えられる．データセット名は，Set の後の 4 個の数字が順に a, b, c, d を表す．
• 追加制約のないデータセットに正解した場合は，上記とは別に 10 点が与えられる．データセット名は All である．

入力例 1

2 0 0 0 2
2
5 6
3
6 10 12

出力例 1

Black
White

1 個目の初期状態について考える．皿を入力の順に皿 1, 2 と呼ぶ．くろうさの最初の手番にできる行動は，以下の 5 通りである：

• 皿 1 から 1 個のキャンディを取って食べる．
• 皿 1 から 2 個のキャンディを取って食べる．
• 皿 2 から 1 個のキャンディを取って食べる．
• 皿 2 から 2 個のキャンディを取って食べる．
• 皿 2 から 3 個のキャンディを取って食べる．

くろうさの必勝法として，最初の手番で行動「皿 2 から 1 個のキャンディを取って食べる」をするものが存在することが証明できる．

入力例 2

3 1 1 0 2
3
15 15 20
2
1 17

出力例 2

White
Black

2 個目の初期状態について考える．皿を入力の順に皿 1, 2 と呼ぶ．くろうさの最初の手番にできる行動は，以下の 3 通りである：

• 皿 1 から 1 個のキャンディを取って食べる．
• 皿 2 から 1 個のキャンディを取って食べる．
• 皿 1 から 1 個のキャンディを取って食べ，同時に，皿 2 から 1 個のキャンディを取って食べる．

くろうさが行動「皿 1 から 1 個のキャンディを取って食べ，同時に，皿 2 から 1 個のキャンディを取って食べる」をすると，皿 1 のキャンディが 0 個，皿 2 のキャンディが 16 個になる．このとき皿 1 にはもう可能な操作が存在しないので，ゲームが終了し，くろうさの勝ちとなる．

入力例 3

4 2 0 1 3
1
1
1
2
3
7 11 9

出力例 3

Black
White
White

1 個目の初期状態においては，唯一の皿に対し可能な操作が存在しないので，初期状態でゲームが終了し，くろうさの勝ちとなる．

2 個目の初期状態においては，できる行動は「唯一の皿から 1 個のキャンディを取り，新しい皿を 1 枚用意してそこに置く」のみである．くろうさがこの行動をすると，2 枚の皿とも可能な操作が存在しなくなるので，ゲームが終了し，しろうさの勝ちとなる．

3 個目の初期状態においては，皿を入力の順に皿 1, 2, 3 と呼ぶと，できる行動の例として「同時に，皿 1, 2, 3 からそれぞれ 1, 10, 4 個のキャンディを取り，新しい皿をそれぞれ 1 枚用意して (皿 1', 2', 3' と呼ぶ) そこに置く」というものが考えられる．くろうさがこの行動をすると，しろうさの手番では，皿 1, 1', 2, 2', 3, 3' があり，キャンディがそれぞれ 6, 1, 1, 10, 5, 4 個置かれている状態になる．このときしろうさの行動では，皿 1, 2', 3, 3' に対して操作を行う．