問題文

3 つの整数 N,A,B が与えられます。

(1,2,\dots,N) の順列 P=(P_1,P_2,\dots,P_N), Q=(Q_1,Q_2,\dots,Q_N) であって、

• (P_{Q_1},P_{Q_2},\dots,P_{Q_N}) の転倒数は A
• (Q_{P_1},Q_{P_2},\dots,Q_{P_N}) の転倒数は B

となるものが存在するか判定し、存在する場合は一つ構築してください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

• 1\le T\le 2\times 10^5
• 1 \leq N \leq 2\times 10^5
• 0 \leq A \leq \frac{N(N-1)}{2}
• 0 \leq B \leq \frac{N(N-1)}{2}
• 1 つの入力ファイルに含まれる N の総和は 2\times 10^5 以下
• 入力は全て整数

入力例 1

3
3 3 1
3 1 2
8 13 11

出力例 1

Yes
1 3 2
2 3 1
No
Yes
2 5 8 4 6 3 7 1
2 1 8 5 3 7 4 6

1 つ目のケースに対する出力例について、(P_{Q_1},P_{Q_2},P_{Q_3})=(3,2,1), (Q_{P_1},Q_{P_2},Q_{P_3})=(2,1,3) です。

問題文

0 以上 M 未満の整数からなる長さ N の整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。

Q 個のクエリが与えられるので順に処理してください。i 番目のクエリは以下で説明されます。

• 整数 x_i,y_i が与えられる。 A の x_i 番目の要素を y_i で更新する。その後、以下の問題を解け。
  • 整数列 A をもとにして頂点数 N の無向グラフ G を作る。頂点には 1,2,\ldots,N までの番号がつけられており、頂点 u,v\ (1\leq u\lt v\leq N) の間には A_u+1\equiv A_v\ (\mathrm{mod}\ M) が成り立つとき辺が張られる。 G の最大マッチングの大きさを求めよ。

制約

• 2\leq N\leq 3\times 10^5
• 1\leq Q\leq 3\times 10^5
• 2\leq M\leq 3\times 10^5
• 0\leq A_i\lt M
• 1\leq x_i\leq N
• 0\leq y_i\lt M
• 入力は全て整数

部分点

この問題には複数の部分点が設定されている。

• 追加の制約 Q=1 を満たすデータセットに正解した場合は 10 点が与えられる。
• 追加の制約 M\leq 100 を満たすデータセットに正解した場合は 10 点が与えられる。

入力例 1

6 3 5
1 1 0 2 0 2
6 0
4 1
5 2
1 2
6 2

出力例 1

1
1
2
3
3

1 つ目のクエリについて、 A_6 が 0 に更新され A=(1,1,0,2,0,0) になります。 G には頂点 1,4 の間と頂点 2,4 の間と頂点 4,5 の間と頂点 4,6 の間に辺が張られるため、G の最大マッチングの大きさは 1 です。

2 つ目のクエリについて、 A_4 が 1 に更新され A=(1,1,0,1,0,0) になります。 G には頂点 3,4 の間に辺が張られるため、G の最大マッチングの大きさは 1 です。

問題文

正整数の多重集合が 良い集合 であるとは、含まれる要素がすべて 2 べきであることをいいます。

非負整数 N に対して、要素の総和が N であるような良い集合それぞれについて要素の総積を計算したとき、それらの総和を f(N) とします。ただし、空集合の要素の総和は 0、総積は 1 として f(0)=1 とします。

非負整数 T,a,b が与えられます。 N_i=(ai+b)\ \mathrm{mod}\ 2^{30} としたとき、 \displaystyle \sum_{i=0}^{T-1}(f(N_i)\ \mathrm{mod}\ 998244353)\oplus i を求めてください。 ここで、 \oplus はビットごとの排他的論理和です。

制約

• 1\leq T\leq 10^7
• 0\leq a,b\lt 2^{30}
• 入力は全て整数

部分点

この問題には複数の部分点が設定されている。

• 追加の制約 T\leq 10^6,a=1,b=0 を満たすデータセットに正解した場合は 10 点が与えられる。
• 追加の制約 T\leq 1000 を満たすデータセットに正解した場合は 10 点が与えられる。

入力例 1

5 1 0

出力例 1

17

N_0=0,N_1=1,N_2=2,N_3=3,N_4=4 です。

• 総和が 0 である良い集合は \lbrace\rbrace であり、 f(0)=1 です。
• 総和が 1 である良い集合は \lbrace1\rbrace であり、 f(1)=1 です。
• 総和が 2 である良い集合は \lbrace1,1\rbrace,\lbrace2\rbrace であり、 f(2)=(1\times 1)+(2)=3 です。
• 総和が 3 である良い集合は \lbrace1,1,1\rbrace,\lbrace1,2\rbrace であり、 f(3)=(1\times 1\times 1)+(1\times 2)=3 です。
• 総和が 4 である良い集合は \lbrace1,1,1,1\rbrace,\lbrace1,1,2\rbrace,\lbrace2,2\rbrace,\lbrace4\rbrace であり、 f(4)=(1\times 1\times 1\times 1)+(1\times 1\times 2)+(2\times 2)+(4)=11 です。

よって、求める答えは (1\oplus 0)+(1\oplus 1)+(3\oplus 2)+(3\oplus 3)+(11\oplus 4)=17 です。

入力例 2

3 1000000000 1000000000

出力例 2

1217611736

N_0=1000000000,N_1=926258176,N_2=852516352 です。

問題文

(1,2,\dots,M) の順列 Q=(Q_1,Q_2,\dots,Q_M) に対し、長さ M-1 の数列 f(Q) を以下のように定めます。

• 長さ M-1 の数列 X を X=(0,0,\dots,0) で初期化する
• 以下の操作を M-1 回行う
  • i=1,2,\dots,M-1 の順に以下を行う
    • Q_i > Q_{i+1} ならば Q_i と Q_{i+1} を入れ替え、X_i に 1 を加える
    • Q_i < Q_{i+1} ならば何もしない
• 最終的な X を f(Q) とする

長さ N-1 の数列 B=(B_1,B_2,\dots,B_{N-1}) が与えられます。(1,2,\dots,N) の順列 P であって f(P)=B を満たすものが存在するか判定し、存在するならばそのようなもののうち辞書順で最小のものを求めてください。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \leq T \leq 1.5 \times 10^5
• 2 \leq N \leq 3 \times 10^5
• 0 \leq B_i \leq N-1
• 入力は全て整数
• 1 つの入力ファイルに含まれる N の総和は 3 \times 10^5 以下

入力例 1

3
4
2 1 1
5
2 0 2 4
6
2 3 2 1 1

出力例 1

3 2 4 1
-1
3 5 4 2 6 1

1 つ目のテストケースについて P=(3,2,4,1) のとき f(P) は次のように計算されます。

• はじめ X=(0,0,0) である
• 1 回目の操作は次のように行われる
  • P_1 > P_2 なので X_1 に 1 を加算し、P_1 と P_2 を入れ替える
    • X=(1,0,0),P=(2,3,4,1) となる
  • P_2 < P_3 なので何もしない
  • P_3 > P_4 なので X_3 に 1 を加算し、P_3 と P_4 を入れ替える
    • X=(1,0,1),P=(2,3,1,4) となる
• 2 回目の操作は次のように行われる
  • P_1 < P_2 なので何もしない
  • P_2 > P_3 なので X_2 に 1 を加算し、P_2 と P_3 を入れ替える
    • X=(1,1,1),P=(2,1,3,4) となる
  • P_3 < P_4 なので何もしない
• 3 回目の操作は次のように行われる
  • P_1 > P_2 なので X_1 に 1 を加算し、P_1 と P_2 を入れ替える
    • X=(2,1,1),P=(1,2,3,4) となる
  • P_2 < P_3 なので何もしない
  • P_3 < P_4 なので何もしない

よって f(P) = (2,1,1) となります。特にこの P が f(P)=B を満たす P のうち辞書順最小のものです。

2 つ目のテストケースについて f(P)=(2,0,2,4) となる順列 P は存在しません。

問題文

長さ N の 0, 1からなる文字列 S が与えられます。
文字列 S に対して以下の 2 種類の操作を繰り返し行うことができます。

• 操作 1：S の中の連続部分文字列 010 を 1 つ選び、 1 に置き換える。

• 操作 2：S の中の連続部分文字列 11 を 1 つ選び、 1 に置き換える。

操作を行うことができる回数の最大値を求めてください。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \leq T \leq 10^5
• 1 \leq N \leq 10^6
• S は 0, 1 からなる長さ N の文字列
• 1 つの入力ファイルに含まれる N の総和は 10^6 以下
• T,N は整数

入力例 1

5
6
010100
4
0110
3
100
2
00
20
01001100000001101001

出力例 1

3
2
0
0
11

1 つ目のテストケースについて、例えば以下のように 3 回の操作を行うことができます。

• 010100 の 3 から 5 文字目の 010 を 1 に置き換え、0110 にする。
• 0110 の 2 から 3 文字目の 11 を 1 に置き換え、010 にする。
• 010 の 1 から 3 文字目の 010 を 1 に置き換え、1 にする。

010100 に対して 4 回以上の操作を行うことはできないため、答えは 3 となります。

問題文

非負整数 L,R,X が二進法で与えられます。長さ R-L+1 の整数列 (L \oplus X,(L+1)\oplus X, \dots, R\oplus X) の転倒数を二進法で求めてください。

ただし、\oplus はビットごとの排他的論理和を表します。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \leq T \leq 2 \times 10^5
• 0 \leq L \leq R \lt 2^{2 \times 10^5}
• 0 \leq X \lt 2^{2 \times 10^5}
• 入力は全て整数
• T は 十進法で与えられる
• L,R,X は二進法で与えられ、先頭に余分な 0 を含まない（ただし 0 は 1 桁の整数とみなす）
• 1 つの入力ファイルに含まれる R の二進法での桁数の総和は 2 \times 10^5 以下
• 1 つの入力ファイルに含まれる X の二進法での桁数の総和は 2 \times 10^5 以下

部分点

追加の制約 T \leq 3000, R \lt 2^{30}, X \lt 2^{30} を満たすデータセットに正解した場合は 10 点が与えられる。

入力例 1

3
101 1000 10
1101 10111010 0
1000110 1110011011101 100011110010

出力例 1

10
0
11100100001101111010100

1 つ目のテストケースについて、L,R,X をそれぞれ十進法で表記すると L=5,R=8,X=2 です。(5\oplus 2, 6\oplus 2, 7\oplus 2, 8\oplus 2)=(7,4,5,10) なので求めるべき転倒数は 2 です。

問題文

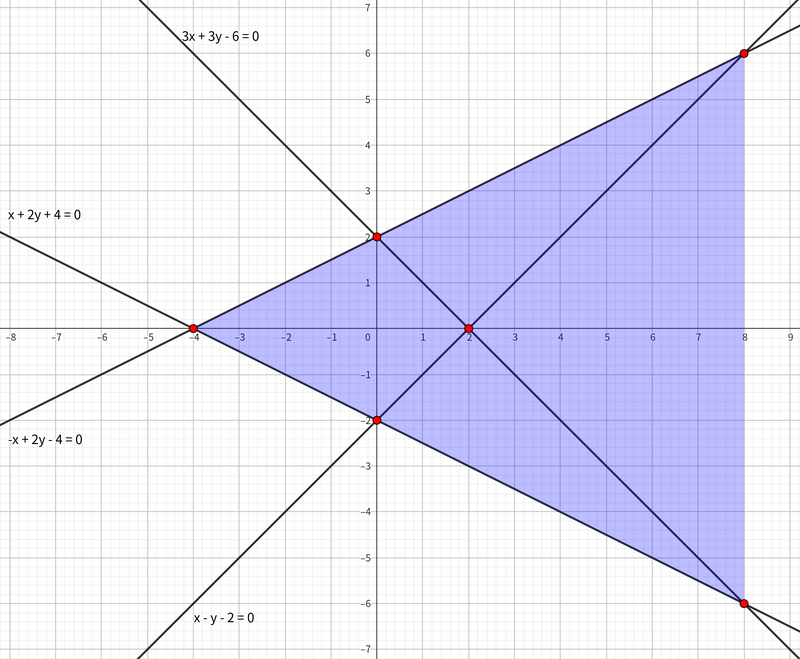
xy 平面上に相異なる N 本の直線があり、 i 番目の直線 \ell_i は a_i x + b_i y + c_i = 0 の形で表されます。 これらの直線群の交点全体の集合を P とします。より厳密には次の通りです。

P = \{ p \in \mathbb{R}^2 \mid \exists i, j \in \{1, 2, \ldots, N\} \, \text{ s.t. } \, p \in \ell_i, \, p \in \ell_j, \, i \neq j \}

このとき、 P の凸包の面積を求めてください。ただし、凸包が空集合、1 点集合または線分である場合、その面積は 0 とします。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \leq T
• 2 \leq N \leq {10}^4
• |a_i|, |b_i|, |c_i| \leq {10}^3
• a_i \neq 0 または b_i \neq 0
• 直線 \ell_i と \ell_j は異なる (i \neq j)
• 1 つの入力ファイルに含まれる N の総和は 2 \times {10}^5 以下
• 入力はすべて整数

入力例 1

3
4
1 -1 -2
3 3 -6
-1 2 -4
1 2 4
3
3 0 5
5 0 18
1 0 7
3
314 159 -1
313 158 -1000
315 160 999

出力例 1

72.0
0
0.0016129032

1 つ目のテストケースでは、 P の凸包は (8, 6), (-4, 0), (8, -6) をこの順に結ぶ三角形であり、その面積は 72 です。

2 つ目のテストケースでは、 3 つの直線は全て平行なため P = \emptyset です。 したがって、 P の凸包の面積は 0 です。

問題文

N \times N のグリッドがあります。上から i 行目、左から j 列目のマスをマス (i,j) と表します。

また、 M 個の整数の 4 つ組 (t_k,i_k,j_k,d_k)\; (k=1,2,\dots,M) が与えられます。(t,i,j,d) は以下を満たします。

• t は 0 または 1
• t=0 ならば 1 \leq i\leq N-1, 1 \leq j \leq N
• t=1 ならば 1 \leq i \leq N, 1 \leq j \leq N-1
• d は 1 または 2

グリッドの各マスに整数を書き込む方法であって、以下の条件をすべて満たすものがあるか判定し、存在するならば一つ構成してください。

• 各マスに書かれている整数は 0 以上 10^9 以下の整数である
• 上下左右に隣接するマスに書かれている整数の差の絶対値は 1 か 2 である
• 各 k=1,2,\dots,M について、以下が成り立つ
  • t_k=0 ならば、マス (i_k,j_k),(i_k+1,j_k) に書かれている整数の差の絶対値は d_k である
  • t_k=1 ならば、マス (i_k,j_k),(i_k,j_k+1) に書かれている整数の差の絶対値は d_k である

制約

• 1 \leq N \leq 1000
• 0 \leq M \leq \min\{2 \times 10^5,2N(N-1)\}
• (t_k,i_k,j_k,d_k) は問題文の条件を満たす
• k \neq \ell ならば (t_k,i_k,j_k) \neq (t_\ell,i_\ell,j_\ell)
• 入力はすべて整数

入力例 1

2 3
0 1 1 2
1 1 1 1
0 1 2 2

出力例 1

Yes
0 1
2 3

他にも、

Yes
5 4
3 2

なども正解になります。

入力例 2

2 3
0 1 1 2
1 1 1 2
1 2 1 1

出力例 2

Yes
0 2
2 3

他にも、

Yes
0 2
2 1

なども正解になります。

入力例 3

2 4
0 1 1 2
1 1 1 2
1 2 1 1
0 1 2 2

出力例 3

No

条件を満たす書き込み方は存在しません。

問題文

頂点に 1 から n までの番号がついた n 頂点の木 t に対し、以下の条件を満たす (1, \dots, n) の順列 p = (p_1, \dots, p_n) の個数を f(t) とおきます。

• i = 1, \dots, n に対し、頂点 p_i と頂点 p_{i + 1} を結ぶ単純パスに含まれる辺が 2 本以下 (ただし、p_{n + 1} = p_1 とする)

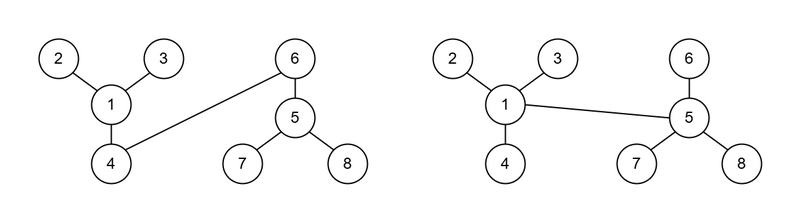
正整数 N, K、および頂点に 1 から N までの番号がついた N 頂点の木 T_0 が与えられます。 T_0 の i 番目の辺は頂点 A_i と頂点 B_i を結びます。

T_0 を K 個つなげて得られる木を 良い木 と呼びます。 より形式的には、頂点に 1 から NK までの番号がついた NK 頂点の木 T が以下の条件を満たすとき、またそのときに限り T を良い木であるとします。

• 1\le i\le N - 1 かつ 0\le k\le K - 1 を満たすすべての整数の組 (i, k) に対し、頂点 (A_i + N\times k) と頂点 (B_i + N\times k) の間に辺が存在する

すべての良い木 T に対する f(T) の総和を 998244353 で割った余りを求めてください。

Q 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1\le Q\le 2\times 10 ^ 5
• 1\le N\le 2\times 10 ^ 5
• 1\le K\le 2\times 10 ^ 5
• 1\le A_i\lt B_i\le N
• 1 つの入力ファイルに含まれる N の総和は 2\times 10 ^ 5 以下
• 入力されるグラフは木
• 入力はすべて整数

入力例 1

5
4 1
1 2
1 3
1 4
4 1
1 2
2 3
3 4
1 4
4 2
1 2
1 3
1 4
6 200000
1 3
2 3
3 4
4 5
4 6

出力例 1

24
8
192
2304
210217795

1 つ目のテストケースについて、どの単純パスも 2 本以下の辺しか含まないため、ありうる順列が全て数えられます。

2 つ目のテストケースについて、数える順列は (1, 2, 4, 3), (1, 3, 4, 2), (2, 1, 3, 4), (2, 4, 3, 1), (3, 1, 2, 4), (3, 4, 2, 1), (4, 2, 1, 3), (4, 3, 1, 2) の 8 通りです。

3 つ目のテストケースについて、すべての 4 頂点の木 T に対する f(T) の総和を求める必要があります。 T_0 が辺を持たない場合があることに注意してください。

4 つ目のテストケースについて、良い木として例えば以下のような木が挙げられます。

問題文

正の奇数 N と (1, 2, \ldots, N) の順列 P = (P_1, P_2, \ldots, P_N) が与えられます。

あなたははじめ数列 A = P を持っており、数列 A に対して以下の操作を繰り返し行うことができます。

• A の奇数長の連続部分列を選ぶ。選んだ連続部分列の中央値を m として、 A から選んだ連続部分列を削除し、その位置に m を挿入する。
  • より厳密には、 1 \leq l \leq r \leq |A| かつ r-l+1 が奇数であるような整数の組 (l, r) を選ぶ。 (A_l, A_{l+1}, \ldots, A_r) の中央値を m として、 A を (A_1, \ldots, A_{l-1}, m, A_{r+1}, \ldots, A_n) で置き換える。

各 k = 1, 2, \ldots, N について、操作を繰り返すことで A を長さ 1 の数列 (k) にすることができるか判定してください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

• 1 \leq T \leq {10}^4
• 3 \leq N \leq 2 \times {10}^5
• N は奇数
• (P_1, P_2, \ldots, P_N) は (1, 2, \ldots, N) の順列
• 1 つの入力ファイルに含まれる N の総和は 2 \times {10}^5 以下
• 入力はすべて整数

部分点

• 追加の制約「 1 つの入力ファイルに含まれる N の総和は 5000 以下」を満たすデータセットに正解した場合は 10 点が与えられる。

入力例 1

2
5
2 3 1 5 4
7
7 6 3 4 5 2 1

出力例 1

00110
0101010

1 つ目のテストケースについて

• k = 3 のとき : (l, r) = (1, 5) を選ぶことで A = (3) になります。
• k = 4 のとき : (l, r) = (1, 3) を選び A = (2, 5, 4) にしたのち、 (l, r) = (1, 3) を選ぶことで A = (4) になります。
• k = 1, 2, 5 のときはそのような操作列が存在しません。

問題文

あおばさんは次の問題を思いつきました。

Max Bracket Score
長さ 2N の整数列 A=(A_1,A_2,\ldots,A_{2N}) が与えられます。長さ 2N の正しい括弧列 s に対して、 s のスコアを次のように定めます。

• s_i が ( であるようなすべての i に対する A_i の総和

長さ 2N の正しい括弧列のスコアとしてあり得る最大の値を求めてください。

この問題はひろせさんにとって簡単だったので、以下のように改題しました。

Shuffle and Max Bracket Score
長さ 2N の整数列 A=(A_1,A_2,\ldots,A_{2N}) が与えられます。 A を一様ランダムにシャッフルした後の Max Bracket Score の答えの期待値を \mathrm{mod}\ 998244353 で求めてください。

Shuffle and Max Bracket Score を解いてください。

制約

• 1\leq N \leq 10^5
• 1\leq A_i\leq 10^9
• 入力は全て整数

部分点

• 追加の制約 N\leq 100 を満たすデータセットに正解した場合は 10 点が与えられる。

入力例 1

1
1 2

出力例 1

499122178

A=(1,2) のとき Max Bracket Score の答えは 1 です。

• s が () のときのスコアは 1 です。

A=(2,1) のとき Max Bracket Score の答えは 2 です。

• s が () のときのスコアは 2 です。

求める期待値は \dfrac{1}{2}(1+2)=\dfrac{3}{2} です。

入力例 2

2
1 2 3 4

出力例 2

831870300

例えば A=(1,2,3,4) のとき Max Bracket Score の答えは 4 です。

• s が ()() のときのスコアは 1+3=4 です。
• s が (()) のときのスコアは 1+2=3 です。

また、 A=(4,3,2,1) のとき Max Bracket Score の答えは 7 です。

• s が ()() のときのスコアは 4+2=6 です。
• s が (()) のときのスコアは 4+3=7 です。

求める期待値は \dfrac{35}{6} です。

入力例 3

4
31415 92653 58979 32384 62643 38327 95028 84197

出力例 3

420993474

問題文

正の整数 s,t が与えられます。あなたは以下の操作を 0 回以上好きな回数行うことができます。

• 1 以上 4 \times 10^{18} 以下の整数 u であって s+u が平方数であるものを選び、s を u で置き換える

s を t に一致させるために必要な操作の回数の最小値、およびその方法を一つ求めてください。

形式的には、以下を全て満たす長さ K の整数列 (u_1,u_2,\dots,u_K) を一つ求めてください。

• K は s を t に一致させるために必要な操作回数の最小値
• i=1,2,\dots,K に対して 1 \leq u_i \leq 4 \times 10^{18}
• u_0=s とすると i=1,2,\dots,K に対して u_{i-1}+u_i は平方数
• u_K=t

なお、本問の制約の下で 10^6 回以下の操作で s を t に一致させる操作方法が必ず存在することが証明できます。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \leq T \leq 3 \times 10^5
• 1 \leq s, t \leq 10^9
• s \ne t
• 1 つの入力ファイルに対する必要な操作回数 (=K) の総和は 10^6 以下
• 入力は全て整数

入力例 1

3
8 3
20 24
998236771 998244353

出力例 1

2 1 3
3 5 76 24
1 998244353

1 つ目のテストケースについて、8+1=9,1+3=4 はともに平方数です。また、1 回の操作で 8 を 3 にすることは出来ません。

問題文

1 から 9 までの数字からなる長さ N の数字列 S と整数 M,K(1\leq K\leq M\leq N) が与えられます。

S を M 個の非空な数字列に分割してそれぞれを 10 進法の整数とみなします。これら M 個の整数のうち大きい方から K 番目のものとしてあり得る最小値を求めてください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

• 1\leq T\leq 10^5
• 1\leq K\leq M\leq N\leq 10^6
• T,N,M,K は整数
• S は 1 から 9 までの数字からなる長さ N の数字列
• 1 つの入力ファイルに含まれる N の総和は 10^6 以下

入力例 1

3
5 2 1
12345
5 3 3
12345
10 7 1
3141592653

出力例 1

123
1
26

1 つ目のテストケースについて、 S を \texttt{123},\texttt{45} のように分割することで 1 番目に大きいものが 123 となり、これが最小です。

2 つ目のテストケースについて、 S を \texttt{1},\texttt{23},\texttt{45} のように分割することで 3 番目に大きいものが 1 となり、これが最小です。

問題文

2N 頂点 M 辺の単純無向グラフ G が与えられます。頂点 i \; (i=1,2,\dots,2N) には整数 \lfloor (i+1)/2 \rfloor が書き込まれています。また、j\;(j=1,2,\dots,M) 番目の辺は頂点 u_j と頂点 v_j を双方向に結びます。

G の頂点からなる列 P=(v_1,v_2,\dots,v_K) が 回文パス であるとは、P が以下の 3 条件を満たすことと定義します。

• K\geq 2
• P は 単純パス である。すなわち、各 k=1,2\dots,K-1 について、頂点 v_k と頂点 v_{k+1} を結ぶ辺が存在し、かつ 1 \leq k < \ell \leq K について、 v_k \neq v_\ell である。
• P の頂点に書かれている整数を順に並べた列は 回文 である。すなわち、各 k=1,2,\dots,\lfloor K/2 \rfloor について、\lfloor (v_k+1)/2 \rfloor = \lfloor (v_{K-k+1}+1)/2 \rfloor である。

各 x=1,2,\dots,N について、x が書き込まれている頂点から始まる回文パスが存在するかどうか判定してください。

制約

• 1 \leq N \leq 2 \times 10^5
• 1 \leq M \leq 4 \times 10^5
• 1 \leq u_j < v_j \leq 2N
• 与えられるグラフは単純
• 入力はすべて整数

入力例 1

4 9
1 3
2 5
2 7
3 5
4 6
4 8
5 6
6 7
6 8

出力例 1

No
Yes
Yes
Yes

x=2,3,4 について、 x が書き込まれている頂点から始まる回文パスの 1 つは以下のとおりです。

• x=2: (3, 5, 6, 4)
• x=3: (5, 6)
• x=4: (7, 6, 8)

入力例 2

3 6
1 3
3 5
2 4
4 6
1 5
1 6

出力例 2

No
Yes
Yes

背景

あおばさんは 2 つのコンテストでの順位の積の値を競う大会に参加し、現在 1 つ目のコンテストが終了しました。
あおばさんは単独優勝できるでしょうか?

問題文

正の整数 N が与えられます。 n=1,2,\dots,N について以下の問題を解いてください。

(1,2,\dots, N) の順列 P=(P_1,P_2,\dots,P_N) であって、m=1,2,\dots,N 全てについて

\[n\neq m\implies nP_n<mP_m\]

が成り立つものの個数を 998244353 で割った余りを求めよ。

制約

• 1 \leq N \leq 5\times 10^5
• 入力は全て整数

部分点

• 追加の制約 N\le1000 を満たすデータセットに正解した場合は 10 点が与えられる。

入力例 1

3

出力例 1

3
1
0

• n=1 のとき条件を満たす順列は P=(1,2,3),(1,3,2),(2,3,1) の 3 つです。
• n=2 のとき条件を満たす順列は P=(3,1,2) の 1 つです。
• n=3 のとき条件を満たす順列は存在しません。　

Universal Cup 参加者へ

この問題は Universal Cup に収録される際に削除されます。そのため、Universal Cup に AtCoder での結果を使用する場合はこの問題以外を先に解くことをおすすめします。

問題文

長さ N の正整数列 A = (A_1,A_2,\dots,A_N) が与えられます。 A に対して以下の操作を 0 回以上繰り返すことができます。

• 整数 i \ (1 \le i \le N-1) を 1 つ選び、 A_i, A_{i+1} をどちらも 0 に置き換える。この操作にはコストが \max(A_i,A_{i+1}) かかる。

A の全ての要素を 0 にするために必要なコストの和の最小値を求めてください。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \le T \le 10^5
• 2 \leq N \leq 2 \times 10^5
• 1 \le A_i \le 10^9
• 1 つの入力ファイルに含まれる N の総和は 2\times 10^5 以下
• 入力は全て整数

入力例 1

4
4
2 6 7 3
2
1 1000000000
20
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
8
123 4567 8912 34 56789 12345 6789 1

出力例 1

12
1000000000
10
72647

1 つ目のテストケースについて、例えば以下のように 3 回の操作を行うことができます。

• A=(2,6,7,3) に対して i = 2 として操作を行い、A=(2,0,0,3) となる。コストが 7 かかる。
• A=(2,0,0,3) に対して i = 1 として操作を行い、A=(0,0,0,3) となる。コストが 2 かかる。
• A=(0,0,0,3) に対して i = 3 として操作を行い、A=(0,0,0,0) となる。コストが 3 かかる。

かかったコストの和は 7+2+3=12 です。A=(0,0,0,0) とするためにかかるコストの和はこれより小さくできないため、12 が答えになります。

Universal Cup 参加者へ

この問題は Universal Cup に収録される際に削除されます。そのため、Universal Cup に AtCoder での結果を使用する場合はこの問題以外を先に解くことをおすすめします。

問題文

N 個の半開区間が与えられます。i 個目の半開区間は整数 L_i,R_i を用いて [L_i,R_i) と表されます。

あなたは以下の操作を任意の回数( 0 回も可)行う事が出来ます。

• 2N 個の整数 L_1,R_1,L_2,R_2,\dots,L_N,R_N のうち 1 つを選び、値を 1 増やすか 1 減らす。

あなたの目標は、N 個の半開区間 [L_1,R_1), [L_2,R_2),\dots,[L_N,R_N) を互いに交わらないようにすることです。 より厳密には、1\le i\lt j\le N なる全ての整数の組 (i,j) について、 「L_i\le x\lt R_i かつ L_j\le x\lt R_j を満たす実数 x が存在しない」ようにすることです。

ただし、 L\ge R のとき半開区間 [L,R) は空集合を表し、空集合は任意の区間と交わらないとします。

目標を達成するために必要な最小の操作回数を求めてください。

T 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1 \le T \le 10^5
• 2 \leq N \leq 2 \times 10^5
• 1 \le L_i\lt R_i \le 10^9
• 1 つの入力ファイルに含まれる N の総和は 2\times 10^5 以下
• 入力は全て整数

入力例 1

4
3
1 4
3 7
6 7
2
1 1000000000
1 1000000000
2
1 2
2 3
4
20 25
3 22
3 23
3 24

出力例 1

2
999999999
0
43

1 つ目のテストケースについて、例えば

• R_1 を 1 減らす
• L_3 を 1 増やす

と操作をすると、3 つの区間は [1,3),[3,7),[7,7) となり、これらは互いに交わりません。
2 回未満の操作で目標を達成することは不可能であることが示せるため、1 つ目のテストケースに対する答えは 2 です。

Universal Cup 参加者へ

この問題は Universal Cup に収録される際に削除されます。そのため、Universal Cup に AtCoder での結果を使用する場合はこの問題以外を先に解くことをおすすめします。

問題文

(, ), ? からなる長さが偶数の文字列 S が与えられます。

あおばさんとひろせさんがゲームを行います。あおばさんが先手で、 S に ? がある限り以下の操作を交互に行います。

• S の ? である文字を 1 つ選び、( または ) で置き換える。

S から ? が無くなったとき、S が正しい括弧列ならあおばさんの勝ち、そうでないならひろせさんの勝ちになります。

お互いに自分が勝つために最適な行動をとったとき、どちらが勝つか判定してください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

• 1\leq T\leq 10^5
• 2\leq |S|\leq 10^6
• S は (, ), ? からなる長さが偶数の文字列
• 一つの入力ファイルに含まれる |S| の総和は 10^6 以下
• T は整数

入力例 1

3
(???
(()())
??????

出力例 1

First
First
Second

1 つ目のテストケースについて、ゲームの進行として以下のようなものが考えられます。

• 始め S は (??? である。
• あおばさんが 4 文字目の ? を ) で置き換える。S は (??) になる。
• ひろせさんが 2 文字目の ? を ) で置き換える。S は ()?) になる。
• あおばさんが 3 文字目の ? を ( で置き換える。S は ()() になる。
• S に ? が残っていないので操作は終了する。S は正しい括弧列であるためあおばさんの勝ちとなる。

1 つ目のテストケースでは、ひろせさんがどのように行動してもあおばさんが勝つことができます。