実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given a graph G consisting of N vertices numbered 1, 2, \ldots, N. Initially, G has no edges.
You will add M undirected edges to G. The final shape of the graph is predetermined, and the i-th edge to be added (1 ≤ i ≤ M) connects vertices u_i and v_i. We will refer to this as edge i.
It is guaranteed that the resulting graph will be simple.
Determine if there exists a permutation (P_1, P_2, \ldots, P_M) of (1, 2, \ldots, M) that satisfies the following conditions, and if such a permutation exists, show an example.
Conditions
You must be able to add all M edges to G by following this procedure:
- For i = 1, 2, \dots, M, repeat the following:
- If there is already a cycle in G containing either vertex u_{P_i} or vertex v_{P_i}, the condition is not satisfied, and the procedure ends.
- Add edge P_i (the undirected edge connecting u_{P_i} and v_{P_i}) to G.
You are given T test cases; solve each of them.
What is a cycle?
A cycle in G is defined as a sequence of vertices (v_0, \dots, v_{L - 1}) and a sequence of edges (e_0, \dots, e_{L - 1}) that satisfy the following conditions:
- L \ge 1
- i \neq j \implies v_i \neq v_j, e_i \neq e_j
- For 0 \le i \le L - 2, edge e_i connects vertices v_i and v_{i+1}
- Edge e_{L-1} connects vertices v_{L-1} and v_0
What does it mean for a graph to be simple?
A graph G is simple if it contains no self-loops or multiple edges.Constraints
- All input values are integers.
- 1 \le T \le 2000
- For each test case:
- 2 \le N \le 4000
- 1 \le M \le 4000
- 1 \le u_i, v_i \le N\ (1 ≤ i ≤ M)
- The graph formed by adding all given edges is simple.
- The sum of N over all test cases is at most 4000.
- The sum of M over all test cases is at most 4000.
Subtasks
30 points will be awarded for passing the test set satisfying:
- T \le 50
- For each test case:
- N \le 100
- M \le 100
- The sum of N over all test cases is at most 100.
- The sum of M over all test cases is at most 100.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Here, \text{case}_i\ (1 ≤ i ≤ T) represents the i-th test case. Each test case is given in the following format:
N M u_1 v_1 u_2 v_2 \vdots u_M v_M
Output
For each test case, if a permutation (P_1, P_2, \ldots, P_M) satisfying the conditions exists, output such a P separated by spaces. If no such permutation exists, output -1.
Sample Input 1
1 4 4 1 2 2 3 3 4 4 2
Sample Output 1
2 4 1 3
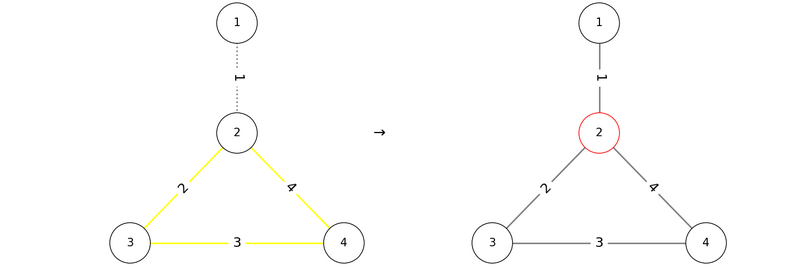
The given graph has the following shape:
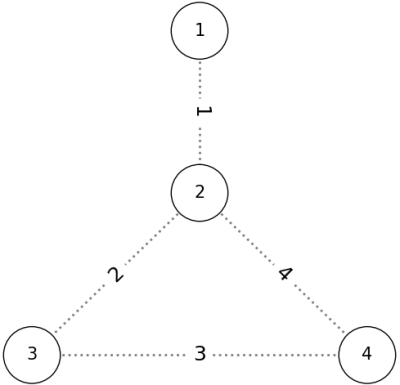
If we add the edges in the order P = (1, 2, 3, 4), the conditions are satisfied as shown below:
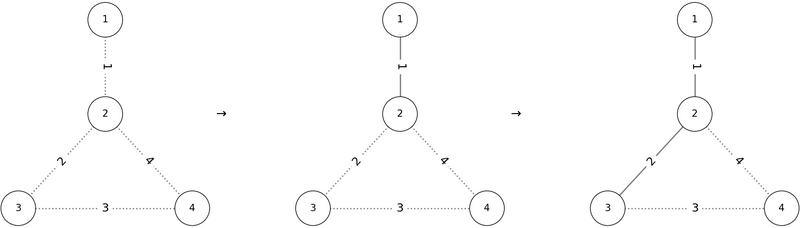
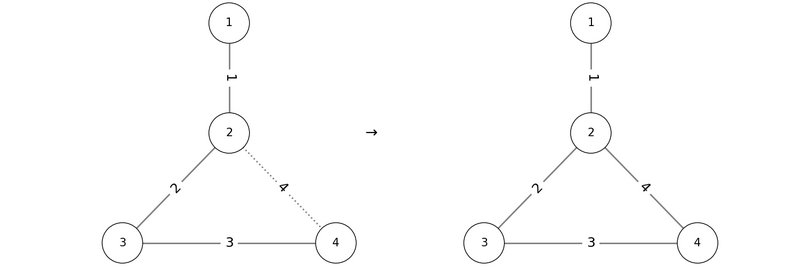
Thus, 1 2 3 4 is one valid output.
However, if we add edges in the order P = (2, 3, 4, 1), a cycle containing vertex 2 is created before edge 1 can be added, so the conditions are not satisfied.
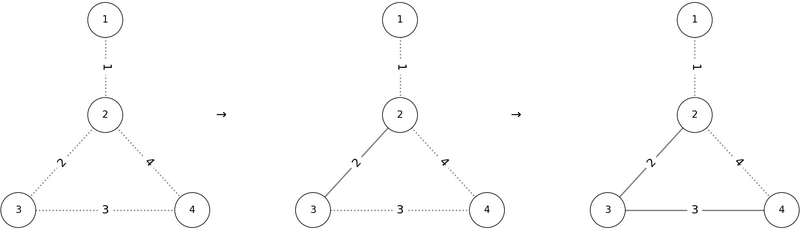
Other valid outputs include P = (1, 4, 3, 2) or P = (2, 4, 1, 3).
Sample Input 2
4 4 5 1 2 2 3 3 4 3 1 1 4 5 3 1 2 2 3 3 4 9 10 3 5 1 8 5 8 4 9 6 7 7 9 1 2 1 4 2 4 4 6 8 10 1 4 3 8 2 5 3 4 1 5 5 8 2 8 5 7 4 5 3 7
Sample Output 2
-1 3 2 1 4 10 2 8 7 9 6 5 3 1 -1
If no valid P exists, output -1. Note that the graph is not necessarily connected.
配点 : 100 点
問題文
N 頂点からなるグラフ G があり、頂点には 1, 2, \ldots, N の番号がついています。はじめ、G には辺がありません。
これから、G に M 本の無向辺を追加します。追加後のグラフの形は決まっており、追加する辺のうち i 番目の辺 (1 ≤ i ≤ M) は頂点 u_i と頂点 v_i を結ぶ辺です。これを辺 i と呼ぶことにします。
追加後のグラフは単純であることが保証されます。
(1, 2, \ldots, M) の順列 (P_1, P_2, \ldots, P_M) であって以下の条件を満たすようなものが存在するかどうか判定し、存在する場合はその一例を示してください。
条件
以下の手順を行って、G に M 本の辺をすべて追加することができる。
- i = 1, 2, \dots, M の順に以下を繰り返す:
- G に頂点 u_{P_i} または頂点 v_{P_i} を含むサイクルが存在するとき、条件は満たされないものとして手順を終了する。
- G に辺 P_i(頂点 u_{P_i} と頂点 v_{P_i} を結ぶ無向辺)を追加する。
T 個のテストケースが与えられるので、それぞれについて解いて下さい。
サイクルとは?
G におけるサイクルとは、頂点の列 (v_0, \dots, v_{L - 1}) と 辺の列 (e_0, \dots, e_{L - 1}) であって以下の条件を満たすもののことを言います。
- L \ge 1
- i \neq j \implies v_i \neq v_j, e_i \neq e_j
- 0 \le i \le L - 2 に対して、辺 e_i は頂点 v_i と頂点 v_{i+1} を結ぶ
- 辺 e_{L-1} は頂点 v_{L-1} と頂点 v_0 を結ぶ
グラフが単純とは?
グラフ G が単純であるとは、G が自己ループ及び多重辺を含まない事を言います。制約
- 入力はすべて整数
- 1 \le T \le 2000
- 各テストケースについて:
- 2 \le N \le 4000
- 1 \le M \le 4000
- 1 \le u_i, v_i \le N\ (1 ≤ i ≤ M)
- 与えられるすべての辺を追加したグラフは単純
- 各入力ファイルについて、N, M の総和はそれぞれ 4000 を超えない
部分点
以下の制約を満たすデータセットに正解した場合は 30 点が与えられる。
- T \le 50
- 各テストケースについて:
- N \le 100
- M \le 100
- 各入力ファイルについて、N, M の総和はそれぞれ 100 を超えない
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
ここで、\text{case}_i\ (1 ≤ i ≤ T) は i 番目のテストケースを表す。各テストケースは以下の形式で与えられる。
N M u_1 v_1 u_2 v_2 \vdots u_M v_M
出力
各テストケースについて、条件を満たす順列 (P_1, P_2, \ldots, P_M) が存在する場合は、そのような P を空白区切りで出力せよ。存在しない場合は、-1 を出力せよ。
入力例 1
1 4 4 1 2 2 3 3 4 4 2
出力例 1
2 4 1 3
与えられたグラフは以下の図のような形をしています。

これに対し、P = (1, 2, 3, 4) の順で辺を追加すると、以下の図のように条件を満たします。


したがって、1 2 3 4 は正しい出力の 1 つです。
しかし、P = (2, 3, 4, 1) の順で辺を追加すると、辺 1 を追加する際に頂点 2 を含むサイクルが存在するため、条件を満たしません。


他にも、P = (1, 4, 3, 2) や P = (2, 4, 1, 3) などが条件を満たします。
入力例 2
4 4 5 1 2 2 3 3 4 3 1 1 4 5 3 1 2 2 3 3 4 9 10 3 5 1 8 5 8 4 9 6 7 7 9 1 2 1 4 2 4 4 6 8 10 1 4 3 8 2 5 3 4 1 5 5 8 2 8 5 7 4 5 3 7
出力例 2
-1 3 2 1 4 10 2 8 7 9 6 5 3 1 -1
条件を満たす P が存在しない場合、-1 を出力して下さい。また、グラフは連結とは限らないことに注意してください。
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given a sequence S of length N, consisting of integers 1, 2, and 3. Determine the number of sequences A consisting of integers 1 and 2 such that the sequence T obtained after performing the following procedure matches S. Output the answer modulo 998244353. It can be proven that the number of such sequences A is finite.
Start with an empty sequence T. Given a sequence A consisting of integers 1 and 2, perform the following process to obtain the sequence T:
- Set a variable C = 0.
- If A contains at least one 1, remove the first occurrence of 1 from A and add 1 to C.
- If A is not empty, remove the first element x of A and add x to C.
- Append C to the end of T.
- If A is empty, terminate the process. Otherwise, return to step 1.
Constraints
- All input values are integers.
- 1 \le N \le 10^6
- 1 \le S_i \le 3
Input
The input is given from Standard Input in the following format:
N S_1 S_2 \dots S_N
Output
Output the number of sequences A that satisfy the conditions, modulo 998244353.
Sample Input 1
2 3 2
Sample Output 1
5
There are 5 possible sequences A that result in T = (3, 2): A = (1, 2, 2), (2, 1, 2), (2, 2, 1), (2, 1, 1, 1), (1, 2, 1, 1).
For example, for A = (2, 1, 1, 1), the process proceeds as follows:
- Remove the first occurrence of 1 in A, which is A_2 = 1. Now A = (2, 1, 1) and C = 1.
- Remove the first element of A, which is A_1 = 2. Now A = (1, 1) and C = 3.
- Append C to the end of T. Now T = (3).
- Remove the first occurrence of 1 in A, which is A_1 = 1. Now A = (1) and C = 1.
- Remove the first element of A, which is A_1 = 1. Now A = () and C = 2.
- Append C to the end of T. Now T = (3, 2).
Sample Input 2
6 3 2 2 3 2 1
Sample Output 2
4
Sample Input 3
5 3 2 1 3 2
Sample Output 3
0
Note that there may be cases where no sequence A produces S, in which case the answer is 0.
配点 : 100 点
問題文
1, 2, 3 からなる長さ N の数列 S が与えられます。1, 2 からなる数列 A であって、以下の問題の答えが S になるようなものの個数を 998244353 で割ったあまりを求めてください。ここで、求める数列 A の個数は有限となることが示せます。
空の数列 T があります。 1, 2 からなる数列 A が与えられます。次の処理を行った後の数列 T を求めてください。
- 変数 C を C = 0 として初期化する。
- A に 1 が含まれるならば、1 のうち最も先頭に近いものを A から取り除き、C に 1 を加算する。
- A が空でないならば、先頭の要素 x を A から取り除き、C に x を加算する。
- T の末尾に C を追加する。
- A が空ならば処理を終了する。そうでないなら 1. に戻る。
制約
- 入力はすべて整数
- 1 \le N \le 10^6
- 1 \le S_i \le 3
入力
入力は以下の形式で標準入力から与えられる。
N S_1 S_2 \dots S_N
出力
条件を満たす数列 A の個数を 998244353 で割ったあまりを出力せよ。
入力例 1
2 3 2
出力例 1
5
問題の答えが (3,2) となる数列 A は (1,2,2), (2,1,2), (2,2,1), (2,1,1,1), (1,2,1,1) の 5 通りです。
例えば (2,1,1,1) の場合は、以下のように問題は処理されます。
- A の 1 のうち最も先頭に近いものである A_2 = 1 を削除する。A = (2,1,1), C = 1 となる。
- A の先頭の要素である A_1 = 2 を削除する。 A = (1,1), C = 3 となる。
- C を T の末尾に追加する。 T = (3) となる。
- A の 1 のうち最も先頭に近いものである A_1 = 1 を削除する。 A = (1), C = 1 となる。
- A の先頭の要素である A_1 = 1 を削除する。 A = (), C = 2 となる。
- C を T の末尾に追加する。 T = (3, 2) となる。
入力例 2
6 3 2 2 3 2 1
出力例 2
4
入力例 3
5 3 2 1 3 2
出力例 3
0
問題の答えが S となる数列 A の個数が 0 個の場合もあります。
実行時間制限: 6 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given an undirected graph G with 2^N + 1 vertices and 2^{N+1} - 1 edges. The vertices are numbered 0, 1, \dots, 2^N, and the edges are numbered 1, 2, \dots, 2^{N+1}-1.
Each edge in G belongs to one of N+1 types, ranging from type 0 to type N.
For type i (0 \le i \le N), there are exactly 2^i edges, which are numbered 2^i+0, 2^i+1, \dots, 2^i+(2^i-1). The edge numbered 2^i + j (0 \leq j \leq 2^i - 1) is an undirected edge of length C_{2^i + j} that connects vertex j \times 2^{N-i} and vertex (j+1) \times 2^{N-i}.
For example, when N = 3, G looks like the following graph:
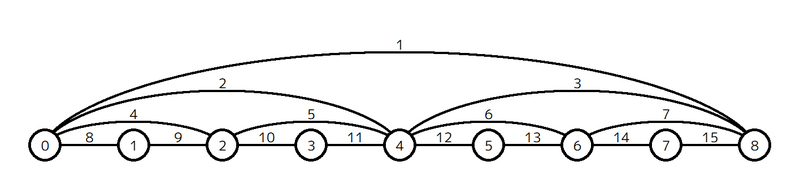
You are given Q queries to process. There are two types of queries:
1 j x: Change the length of edge j to x.2 s t: Find the shortest path length from vertex s to vertex t.
Constraints
- All input values are integers.
- 1 \le N \le 18
- 1 \le C_j \le 10^7 (1 \le j \le 2^{N+1}-1)
- 1 \le Q \le 2 \times 10^5
- In the query
1 j x, 1 \le j \le 2^{N+1}-1 and 1 \le x \le 10^7. - In the query
2 s t, 0 \le s < t \le 2^N. - There is at least one
2 s tquery.
Partial Score
30 points will be awarded for passing the testset satisfying the additional constraint: There is no 1 j x query.
Input
The input is given in the following format. Note that vertex numbering starts from 0, while edge numbering starts from 1.
N
C_1 C_2 \cdots C_{2^{N+1}-1}
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
Here, \text{query}_i represents the i-th query. Each query is given in one of the following formats:
1 j x
2 s t
Output
Let m be the number of queries of type 2 s t. Output m lines, where the i-th line contains the answer to the i-th 2 s t query.
Sample Input 1
3 7 1 14 3 9 4 8 2 6 5 5 13 8 2 3 10 2 0 1 2 0 4 2 4 6 2 4 8 2 3 5 1 6 30 2 3 5 2 4 6 1 1 10000000 2 0 8
Sample Output 1
2 1 4 8 17 18 13 15
- In the 1st query, using edge 8, the path 0 \to 1 results in a total distance of 2.
- In the 2nd query, using edge 2, the path 0 \to 4 results in a total distance of 1.
- In the 3rd query, using edge 6, the path 4 \to 6 results in a total distance of 4.
- In the 4th query, using edges 2, 1, the path 4 \to 0 \to 8 results in a total distance of 8.
- In the 5th query, using edges 11, 6, 13, the path 3 \to 4 \to 6 \to 5 results in a total distance of 17.
- In the 6th query, the length of edge 6 is updated from 4 to 30.
- In the 7th query, using edges 11, 12, the path 3 \to 4 \to 5 results in a total distance of 18.
- In the 8th query, using edges 2, 1, 15, 14, the path 4 \to 0 \to 8 \to 7 \to 6 results in a total distance of 13.
- In the 9th query, the length of edge 1 is updated from 7 to 10000000.
- In the 10th query, using edges 2, 3, the path 0 \to 4 \to 8 results in a total distance of 15.
配点 : 100 点
問題文
2^N + 1 頂点 2^{N+1} - 1 辺の無向グラフ G が与えられます。頂点には 0, 1, \dots, 2^N の番号が、辺には 1, 2, \dots, 2^{N+1}-1 の番号が割り振られています。
G の辺にはタイプ 0 からタイプ N までの N+1 個の種類があります。
タイプ i (0 \le i \le N) の辺は全部で 2^i 本あり、番号 2^i+0, 2^i+1, \dots, 2^i+(2^i-1) が割り当てられています。番号 2^i + j (0 \le j \le 2^i-1) の辺は、頂点 j \times 2^{N-i} と頂点 (j+1) \times 2^{N-i} を結ぶ長さ C_{2^i + j} の無向辺です。
例えば N = 3 の場合、G は以下のようなグラフになります。

Q 個のクエリが与えられるので、順に処理してください。与えられるクエリには以下の 2 種類があります。
1 j x: 辺 j の長さを x に変更する。2 s t: 頂点 s から頂点 t への最短経路の長さを求める。
制約
- 入力はすべて整数
- 1 \le N \le 18
- 1 \le C_j \le 10^7 (1 \le j \le 2^{N+1}-1)
- 1 \le Q \le 2 \times 10^5
1 j xのクエリにおいて、1 \le j \le 2^{N+1}-1 かつ 1 \le x \le 10^7 である2 s tのクエリにおいて、0 \le s < t \le 2^N である2 s tのクエリが 1 つ以上存在する
部分点
以下の制約を満たすデータセットに正解した場合は 30 点が与えられる。
1 j xのクエリが存在しない
入力
入力は以下の形式で与えられる。頂点番号は 0 から始まるのに対し、辺番号は 1 から始まることに注意せよ。
N
C_1 C_2 \cdots C_{2^{N+1}-1}
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
ここで、\text{query}_i は i 個目のクエリを表す。各クエリは以下のいずれかの形式で与えられる。
1 j x
2 s t
出力
2 s t のクエリの個数を m として、m 行出力せよ。そのうち i 行目には、i 個目の 2 s t のクエリの答えを出力せよ。
入力例 1
3 7 1 14 3 9 4 8 2 6 5 5 13 8 2 3 10 2 0 1 2 0 4 2 4 6 2 4 8 2 3 5 1 6 30 2 3 5 2 4 6 1 1 10000000 2 0 8
出力例 1
2 1 4 8 17 18 13 15
- 1 個目のクエリでは、辺 8 を用いて 0 \to 1 と移動することで最短距離 2 を達成できます。
- 2 個目のクエリでは、辺 2 を用いて 0 \to 4 と移動することで最短距離 1 を達成できます。
- 3 個目のクエリでは、辺 6 を用いて 4 \to 6 と移動することで最短距離 4 を達成できます。
- 4 個目のクエリでは、辺 2, 1 を用いて 4 \to 0 \to 8 と移動することで最短距離 8 を達成できます。
- 5 個目のクエリでは、辺 11, 6, 13 を用いて 3 \to 4 \to 6 \to 5 と移動することで最短距離 17 を達成できます。
- 6 個目のクエリでは、辺 6 の長さを 4 から 30 に変更します。
- 7 個目のクエリでは、辺 11, 12 を用いて 3 \to 4 \to 5 と移動することで最短距離 18 を達成できます。
- 8 個目のクエリでは、辺 2, 1, 15, 14 を用いて 4 \to 0 \to 8 \to 7 \to 6 と移動することで最短距離 13 を達成できます。
- 9 個目のクエリでは、辺 1 の長さを 7 から 10000000 に変更します。
- 10 個目のクエリでは、辺 2, 3 を用いて 0 \to 4 \to 8 と移動することで最短距離 15 を達成できます。
実行時間制限: 8 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given non-negative integers A, B, and C. Define a sequence of non-negative integers X = (X_1, X_2, \dots) as follows:
- X_1 = A
- X_2 = B
- X_{i+2} = (X_i \oplus X_{i+1}) + C\ \ (i=1,2,\dots)
Here, \oplus represents the bitwise XOR operation.
You are also given a positive integer N. Calculate X_N \bmod 998244353.
Constraints
- All input values are integers.
- 0 \leq A, B, C < 2^{20}
- 1 \leq N \leq 10^{18}
Input
The input is given from Standard Input in the following format:
A B C N
Output
Output X_N \bmod 998244353.
Sample Input 1
1 2 3 4
Sample Output 1
7
X = (1, 2, 6, 7, \dots). Here, X_4 = 7 is the answer.
Sample Input 2
123 456 789 123456789
Sample Output 2
567982455
Sample Input 3
0 0 0 1000000000000000000
Sample Output 3
0
配点 : 100 点
問題文
非負整数 A,B,C が与えられます。非負整数列 X=(X_1,X_2,\dots) を次のように定めます。
- X_1=A
- X_2=B
- X_{i+2}=(X_{i}\oplus X_{i+1})+C\ (i=1,2,\dots)
ただし、二項演算 \oplus はビットごとの排他的論理和 (bitwise XOR) を表します。
正整数 N が与えられます。 X_N\bmod 998244353 を求めてください。
制約
- 入力はすべて整数
- 0\le A,B,C\lt 2^{20}
- 1\le N\le 10^{18}
入力
入力は以下の形式で標準入力から与えられる。
A B C N
出力
X_N \bmod 998244353 を出力せよ。
入力例 1
1 2 3 4
出力例 1
7
X=(1,2,6,7,\dots) です。 X_4=7 が答えとなります。
入力例 2
123 456 789 123456789
出力例 2
567982455
入力例 3
0 0 0 1000000000000000000
出力例 3
0
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
On the xy-plane, there are N points labeled 1, 2, \dots, N. The coordinates of point i (1 \le i \le N) are (X_i, Y_i).
There is a robot at the origin of this plane. Your task is to control the robot to visit all the points 1, 2, \dots, N in this order.
The robot has a string variable S, which is initially an empty string.
You can move the robot using the following four types of operations:
- Operation 1: Increase the robot's x coordinate by 1 and append
Xto the end of S. This operation costs 1. - Operation 2: Increase the robot's y coordinate by 1 and append
Yto the end of S. This operation costs 1. - Operation 3: Decrease the robot's x coordinate by 1 and remove the last character of S. This operation can only be performed if the last character of S is
X. This operation costs 0. - Operation 4: Decrease the robot's y coordinate by 1 and remove the last character of S. This operation can only be performed if the last character of S is
Y. This operation costs 0.
Find the minimum cost required for the robot to visit all points 1, 2, \dots, N in this order.
Constraints
- All input values are integers.
- 1 \le N \le 500
- 0 \le X_i, Y_i \le 10^9
Input
The input is given from Standard Input in the following format:
N X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
Output
Output the minimum cost required for the robot to visit all points in order.
Sample Input 1
2 3 3 1 2
Sample Output 1
6
By performing Operation 1 once, Operation 2 three times, and Operation 1 twice, you can reach point 1.
Then, by performing Operation 3 twice and Operation 4 once, you can reach point 2.
The total cost of this sequence of operations is the sum of the number of times Operations 1 and 2 are performed, which is 6.
Sample Input 2
3 2 2 3 3 1 3
Sample Output 2
7
配点 : 100 点
問題文
xy 平面上に 1, 2, \dots, N の番号が付けられた N 個の点があります。点 i (1 \le i \le N) の座標は (X_i, Y_i) です。
この平面上の原点にロボットがあります。あなたはこのロボットを操縦して、点 1, 2, \dots, N を この順にすべて 訪れなければなりません。
ロボットは文字列変数 S を持っています。はじめ、S は空文字列です。
あなたは以下の 4 種類の操作でロボットを動かすことができます。
- 操作 1 : ロボットの x 座標を 1 増やし、S の末尾に
Xを追加する。この操作には 1 のコストがかかる。 - 操作 2 : ロボットの y 座標を 1 増やし、S の末尾に
Yを追加する。この操作には 1 のコストがかかる。 - 操作 3 : ロボットの x 座標を 1 減らし、S の末尾の文字を削除する。この操作は S の末尾の文字が
Xであるときのみ行える。この操作にコストはかからない。 - 操作 4 : ロボットの y 座標を 1 減らし、S の末尾の文字を削除する。この操作は S の末尾の文字が
Yであるときのみ行える。この操作にコストはかからない。
点 1, 2, \dots, N をこの順に訪れるのにかかるコストの最小値を求めてください。
制約
- 入力はすべて整数
- 1 \le N \le 500
- 0 \le X_i, Y_i \le 10^9
入力
入力は以下の形式で標準入力から与えられる。
N X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
出力
ロボットが点 1, 2, \dots, N をこの順に訪れるのにかかるコストの最小値を出力せよ。
入力例 1
2 3 3 1 2
出力例 1
6
操作 1 を 1 回、操作 2 を 3 回、操作 1 を 2 回することで、点 1 を訪れることができ、 続けて、操作 3 を 2 回、操作 4 を 1 回することで、点 2 を訪れることができます。
上記の一連の操作のコストは、操作 1, 2 を行った回数の合計である 6 になります。
入力例 2
3 2 2 3 3 1 3
出力例 2
7
実行時間制限: 3 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given N lines on the xy-plane. The i-th line (1 \le i \le N) passes through two distinct points (a_i, b_i) and (c_i, d_i). Specifically, (a_1, b_1, c_1, d_1) = (0, 0, 1, 0) and (a_2, b_2, c_2, d_2) = (0, 0, 0, 1). That is, the first line represents the x-axis, and the second line represents the y-axis.
Alice is on the xy-plane. She can perform the following operation any number of times (including zero):
Choose one of the N given lines. Alice moves to the position symmetric to her current position with respect to the chosen line.
Additionally, we define that point P is reachable from point S if the following condition is satisfied:
For any real number \varepsilon > 0, there exists a point Q such that the Euclidean distance between Q and P is at most \varepsilon, and Alice can move from S to Q in a finite number of operations.
Answer Q queries.
For the i-th query (1 \le i \le Q), you are given integers X_i, Y_i, Z_i, W_i. Output Yes if (Z_i, W_i) is reachable from (X_i, Y_i). Otherwise, output No.
Solve the problem for T test cases.
Constraints
- All input values are integers.
- 1 \le T \le 100
- For each test case:
- 2 \le N \le 2000
- 1 \le Q \le 2000
- -10^8 \le a_i, b_i, c_i, d_i \le 10^8 \ (1 \le i \le N)
- (a_i, b_i) \neq (c_i, d_i)
- (a_1, b_1, c_1, d_1) = (0, 0, 1, 0)
- (a_2, b_2, c_2, d_2) = (0, 0, 0, 1)
- All given lines are distinct.
- -10^8 \le X_i, Y_i, Z_i, W_i \le 10^8 \ (1 \le i \le Q)
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Here, \text{case}_i represents the i-th test case. Each test case is given in the following format:
N a_1 b_1 c_1 d_1 a_2 b_2 c_2 d_2 \vdots a_N b_N c_N d_N Q X_1 Y_1 Z_1 W_1 X_2 Y_2 Z_2 W_2 \vdots X_Q Y_Q Z_Q W_Q
Output
For each test case, output Q lines. The i-th line (1 \le i \le Q) should contain the answer to the i-th query.
The judge is case-insensitive for Yes and No.
Sample Input 1
2 3 0 0 1 0 0 0 0 1 0 2 2 0 4 1 0 2 3 1 -2 -1 2 1 1 -1 0 3 3 3 3 3 0 0 1 0 0 0 0 1 -2 1 2 3 2 2 1 -1 5 -1 -1 3 3
Sample Output 1
Yes Yes No Yes Yes Yes
Let us explain the first test case. For the first query, Alice can use the second and third lines in sequence to move (1, 0) \to (-1, 0) \to (2, 3). Thus, (2, 3) is reachable from (1, 0). Note that for the fourth query, if (X_i, Y_i) = (Z_i, W_i), the destination is always reachable.
Now let us explain the second test case. For the first query, Alice can use the first and third lines in sequence to move (2, 1) \to (2, -1) \to \left(-\frac{6}{5}, \frac{27}{5}\right). The distance between (-1, 5) and \left(-\frac{6}{5}, \frac{27}{5}\right) is \frac{1}{\sqrt{5}}. This means that for \varepsilon \ge \frac{1}{\sqrt{5}}, Alice can find a point Q that satisfies the "reachable" condition. Moreover, for any \varepsilon > 0, Alice can find such a point Q. As a result, (2, 1) is reachable from (-1, 5).
配点 : 100 点
問題文
xy 平面上に N 本の直線が与えられます。i 本目 (1 \le i \le N) の直線は異なる 2 点 (a_i,b_i),(c_i,d_i) を通る直線です。ただし、(a_1,b_1,c_1,d_1)=(0,0,1,0)、(a_2,b_2,c_2,d_2)=(0,0,0,1) です。すなわち、1 本目の直線は x 軸を表しており、2 本目の直線は y 軸を表しています。
Alice が xy 平面上にいます。Alice は、以下の操作を 0 回以上好きな回数行うことができます。
与えられた N 本の直線のうち 1 つを選ぶ。Alice は、選んだ直線について現在位置と線対称な位置に移動する。
また、点 S から点 P に到達可能であるということを、次のように定義します。
任意の実数 \varepsilon >0 について、P とのユークリッド距離が \varepsilon 以下であるような点 Q が存在して、Alice が S から Q に有限回の操作で移動できる。
Q 個のクエリに答えてください。
i 番目 (1 ≤ i ≤ Q) のクエリでは、整数 X_i,Y_i,Z_i,W_i が与えられるので、(X_i,Y_i) から (Z_i,W_i) に到達可能であるならば Yes を、そうでないならば No を出力してください。
T 個のテストケースについて解いてください。
制約
- 入力はすべて整数
- 1 \le T \le 100
- 各テストケースについて:
- 2 \le N \le 2000
- 1 \le Q \le 2000
- -10^8 \le a_i,b_i,c_i,d_i \le 10^8 \ (1 \le i \le N)
- (a_i,b_i) \ne (c_i,d_i)
- (a_1,b_1,c_1,d_1)=(0,0,1,0)
- (a_2,b_2,c_2,d_2)=(0,0,0,1)
- 与えられる直線はすべて異なる
- -10^8 \le X_i,Y_i,Z_i,W_i \le 10^8 \ (1 \le i \le Q)
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
ここで、\text{case}_i は i 番目のテストケースを表す。各テストケースは以下の形式で与えられる。
N a_1 b_1 c_1 d_1 a_2 b_2 c_2 d_2 \vdots a_N b_N c_N d_N Q X_1 Y_1 Z_1 W_1 X_2 Y_2 Z_2 W_2 \vdots X_Q Y_Q Z_Q W_Q
出力
各テストケースに対して、Q 行出力せよ。そのうち i 行目 (1 ≤ i ≤ Q) には、i 番目のクエリの答えを出力せよ。
なお、ジャッジは Yes と No の大文字小文字を区別しない。
入力例 1
2 3 0 0 1 0 0 0 0 1 0 2 2 0 4 1 0 2 3 1 -2 -1 2 1 1 -1 0 3 3 3 3 3 0 0 1 0 0 0 0 1 -2 1 2 3 2 2 1 -1 5 -1 -1 3 3
出力例 1
Yes Yes No Yes Yes Yes
最初のテストケースについて述べます。1 つ目のクエリについて、2 本目、3 本目の直線を順に使うことで、(1,0) \rightarrow (-1,0) \rightarrow (2,3) と移動することができるので、(1,0) から (2,3) は到達可能です。4 つ目のクエリについて、(X_i,Y_i)=(Z_i,W_i) であるときは常に到達可能なことに注意してください。
2 番目のテストケースについて述べます。1 つ目のクエリについて、1 本目、3 本目と順に使うと、(2,1) \rightarrow (2,-1) \rightarrow (-\frac{6}{5},\frac{27}{5}) と移動することができます。(-1,5) と (-\frac{6}{5},\frac{27}{5}) の距離は \frac{1}{\sqrt{5}} なので、\varepsilon \ge \frac{1}{\sqrt{5}} に対しては、問題文中の到達可能の条件を満たすような Q として (-\frac{6}{5},\frac{27}{5}) をとることができます。同様に、任意の \varepsilon > 0 に対しても Q をとることができるため、(2,1) から (-1,5) は到達可能です。
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given a tree A with N vertices. The vertices of A are numbered 1, 2, \dots, N, and the i-th edge (1 \leq i \leq N-1) connects vertices u_i and v_i of A.
Additionally, you are given another tree B with N vertices. The vertices of B are also numbered 1, 2, \dots, N, and the j-th edge (1 \leq j \leq N-1) connects vertices x_j and y_j of B.
Your task is to find a pair of permutations ((P_1, P_2, \dots, P_{N-1}), (Q_1, Q_2, \dots, Q_{N-1})) that satisfies the following conditions:
Conditions
Perform the following operations 1. and 2. in order for k = 1, 2, \dots, N-1. After completing operations 1. and 2. for each k, both A and B must remain as trees.
- In tree A, remove the edge connecting vertices u_{P_k} and v_{P_k}, and add an edge connecting vertices x_{Q_k} and y_{Q_k}.
- In tree B, remove the edge connecting vertices x_{Q_k} and y_{Q_k}, and add an edge connecting vertices u_{P_k} and v_{P_k}.
It can be proven that under the constraints of this problem, a valid solution always exists.
Constraints
- All input values are integers.
- 2 \leq N \leq 1000
- 1 \leq u_i, v_i, x_j, y_j \leq N
- The given A and B form trees.
Input
The input is given from Standard Input in the following format:
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
x_1 y_1
x_2 y_2
\vdots
x_{N-1} y_{N-1}
Output
Output the answer in the following format:
P_1 P_2 \cdots P_{N-1}
Q_1 Q_2 \cdots Q_{N-1}
Sample Input 1
4 1 2 2 3 3 4 1 2 2 4 2 3
Sample Output 1
3 1 2 2 1 3
Before the operation, A is a path graph, and B is a star graph.
After the operation for k = 1, A becomes a star graph, and B becomes a path graph.
In the operations for k = 2, the same edge (in terms of vertex numbers) is removed and added, so the shape of the tree remains unchanged.
After completing the operations for k = 3, the original shapes of trees A and B are completely swapped.
Sample Input 2
2 1 2 2 1
Sample Output 2
1 1
Sample Input 3
7 1 2 1 3 2 4 2 5 3 6 3 7 1 5 1 6 1 7 5 2 6 3 7 4
Sample Output 3
1 2 3 4 5 6 1 2 6 4 5 3
配点 : 100 点
問題文
N 頂点の木 A が与えられます。A の頂点には 1,2,\dots ,N の番号がついており、i 番目 (1 ≤ i ≤ N - 1) の辺は A の頂点 u_i,v_i を結んでいます。
さらに、N 頂点の木 B が与えられます。B の頂点にも 1,2,\dots ,N の番号がついており、j 番目 (1 ≤ j ≤ N - 1) の辺は B の頂点 x_j,y_j を結んでいます。
次の条件を満たす (1,2,\dots ,N-1) の順列の組 ((P_1,P_2,\dots,P_{N-1}),(Q_1,Q_2,\dots ,Q_{N-1})) を 1 つ求めてください。
条件
k=1,2,\dots ,N-1 の順に次の 1. と 2. の操作を行う。各 k において 1. と 2. の操作が終わったとき、A も B も再び木となる。
- 木 A において、頂点 u_{P_k},v_{P_k} を結ぶ辺を削除し、頂点 x_{Q_k},y_{Q_k} を結ぶ辺を追加する。
- 木 B において、頂点 x_{Q_k},y_{Q_k} を結ぶ辺を削除し、頂点 u_{P_k},v_{P_k} を結ぶ辺を追加する。
なお、この問題の制約下で、答えは必ず存在することが証明できます。
制約
- 入力はすべて整数
- 2\le N\le 1000
- 1\le u_i, v_i, x_j, y_j\le N
- 与えられる A,B は木をなす
入力
入力は以下の形式で標準入力から与えられる。
N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
x_1 y_1
x_2 y_2
\vdots
x_{N-1} y_{N-1}
出力
以下の形式で出力せよ。
P_1 P_2 \cdots P_{N-1}
Q_1 Q_2 \cdots Q_{N-1}
入力例 1
4 1 2 2 3 3 4 1 2 2 4 2 3
出力例 1
3 1 2 2 1 3
操作前の木は、 A はパスグラフ、 B はスターグラフになっています。
k=1 の操作が終わったとき、A がスターグラフに、 B がパスグラフになっています。
k=2 の操作では結んでいる頂点の番号が同じ辺を削除・追加しているので、木の形は変わりません。
k=3 の操作が終わったとき、最初の A,B の木の形がちょうど入れ替わっています。
入力例 2
2 1 2 2 1
出力例 2
1 1
入力例 3
7 1 2 1 3 2 4 2 5 3 6 3 7 1 5 1 6 1 7 5 2 6 3 7 4
出力例 3
1 2 3 4 5 6 1 2 6 4 5 3
実行時間制限: 4 sec / メモリ制限: 2048 MiB
配点 : 100 点
Problem Statement
A set of points U in the xy-plane is called good if no point in U lies in the interior of the convex hull of U. Note that the empty set is considered good.
You are given N distinct points v_1, v_2, \dots, v_N in the xy-plane. The coordinates of the point v_i are (x_i, y_i). No three distinct points are collinear.
Count the number of subsets S of V = \lbrace v_1, v_2, \dots, v_N \rbrace such that both S and V \setminus S are good sets.
Constraints
- All input values are integers.
- 1 \le N \le 40
- |x_i|,|y_i|\le 10^6
- (x_i,y_i)\neq (x_j,y_j)\ (i\neq j)
- No three distinct points are collinear.
Input
The input is given in the following format:
N x_1 y_1 x_2 y_2 \vdots x_N y_N
Output
Output the answer.
Sample Input 1
4 0 0 3 0 0 3 1 1
Sample Output 1
14
Except for \emptyset and V, all other sets S satisfy the condition.
Sample Input 2
8 1 0 2 0 3 1 3 2 2 3 1 3 0 2 0 1
Sample Output 2
256
Sample Input 3
10 0 0 1 1 7 1 1 7 3 2 2 3 4 2 2 4 5 4 4 5
Sample Output 3
0
配点 : 100 点
問題文
xy 平面上の点の集合 U が 良い集合 であるとは、 U の凸包の内部に U の点を含まないことを言います。ただし、空集合は良い集合です。
xy 平面上の相異なる N 個の点 v_1,v_2,\dots ,v_N が与えられます。点 v_i の座標は (x_i,y_i) です。これらのうちどの相異なる 3 点も同一直線上に位置することはありません。
V = \lbrace v_1, v_2, \dots, v_N \rbrace の部分集合 S であって、 S と V \setminus S がともに良い集合となるようなものの個数を数えてください。
制約
- 入力はすべて整数
- 1\le N\le 40
- |x_i|,|y_i|\le 10^6
- (x_i,y_i)\neq (x_j,y_j)\ (i\neq j)
- どの相異なる 3 点も同一直線上に位置しない
入力
入力は以下の形式で標準入力から与えられる。
N x_1 y_1 x_2 y_2 \vdots x_N y_N
出力
答えを出力せよ。
入力例 1
4 0 0 3 0 0 3 1 1
出力例 1
14
\emptyset と V 以外の S が条件を満たします。
入力例 2
8 1 0 2 0 3 1 3 2 2 3 1 3 0 2 0 1
出力例 2
256
入力例 3
10 0 0 1 1 7 1 1 7 3 2 2 3 4 2 2 4 5 4 4 5
出力例 3
0
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
This is an interactive problem, where your program interacts with the judge system via Standard Input and Output.
You are given integers N, K, and Q.
The judge holds a hidden permutation (a_1, a_2, \dots, a_N) of (1, 2, \dots, N).
You may ask up to Q queries to the judge, where each query is as follows:
- Choose a subset S from \lbrace 1, 2, \dots, N \rbrace. The judge will return the number of distinct pairs (i, j) such that i < j and |a_i - a_j| \leq K where i, j \in S.
Let x be the index t where a_t = 1, and y be the index t where a_t = N. Your task is to identify the set \lbrace x, y \rbrace. (You do not need to distinguish which is x and which is y.)
The judge is non-adaptive, that means the permutation (a_1, a_2, \dots, a_N) is fixed before any interaction begins.
Constraints
- All input values are integers.
- N = 20000
- 1 \leq K \leq 10
- Q = 30(K + 1)
Partial Score
30 points will be awarded for passing the test set satisfying the additional constraint K = 10.
Input and Output
This is an interactive problem.
First, read integers N, K, and Q from the Standard Input:
N K Q
Then, repeat the following process until you identify the set \lbrace x, y \rbrace:
For a query, output the following format to the Standard Output:
? s_1s_2 \dots s_N
Here, s_1 s_2 \dots s_N is a binary string of length N representing the subset S, where s_i = {}1 if i \in S, and s_i = {}0 otherwise.
The response to your query will be provided in the Standard Input in the following format:
T
Here, T is the answer to the query, representing the number of distinct pairs (i, j) such that i < j and |a_i - a_j| \leq K where i, j \in S.
Once you identify the set \lbrace x, y \rbrace, output the two elements in the following format (order does not matter) and terminate your program immediately:
! x y
Notes
- Print a newline and flush Standard Output at the end of each message. Otherwise, you may get a TLE verdict.
- If your query format is invalid or you exceed the number of queries, the judge will respond with T = -1. If you receive this response, you should immediately terminate your program. Otherwise, you may get a TLE verdict.
- Beware that unnecessary newlines are considered as malformed.
Sample Interaction
The following is a sample interaction for N = 5, K = 2, Q = 90. Note that this example does not meet the constraints and will not appear in the test cases.
| Input | Output | Explanation |
|---|---|---|
| The judge holds the permutation (3, 5, 2, 1, 4). | ||
5 2 90 |
First, integers N, K, and Q are provided. | |
? 11000 |
You query with S = \lbrace 1, 2 \rbrace. | |
1 |
Only the pair (1, 2) satisfies the condition, so the judge responds with 1. |
|
? 10011 |
You query with S = \lbrace 1, 4, 5 \rbrace. | |
2 |
The pairs (1, 4) and (1, 5) satisfy the condition, so the judge responds with 2. |
|
! 2 4 |
You output \lbrace 2, 4 \rbrace as the answer. Since a_4 = 1 and a_2 = N, this output is correct. |
配点 : 100 点
問題文
この問題は インタラクティブな問題(あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題)です。
整数 N, K, Q が与えられます。 ジャッジシステムは (1, 2, \dots, N) の順列 (a_1, a_2, \dots, a_N) を隠し持っています。 あなたはジャッジに Q 回まで次のような質問をすることが出来ます。
- \lbrace 1, 2, \dots, N \rbrace の部分集合 S を選ぶ。S の異なる 2 元の組 (i,j) であって、 i<j かつ |a_i-a_j|\leq K であるような組の個数を聞く。
a_t=1 となるような t を x とし、 a_t=N となるような t を y とします。 集合 \lbrace x,y \rbrace を特定してください。(どちらが x でどちらが y かを特定する必要はありません。)
なお、ジャッジは適応的 (adaptive) ではなく、順列 (a_1, a_2, \dots, a_N) はやりとりの前から固定されています。
制約
- 入力はすべて整数
- N = 20000
- 1 \leq K \leq 10
- Q = 30(K + 1)
部分点
追加の制約 K = 10 を満たすデータセットに正解した場合は 30 点が与えられる。
入出力
この問題はインタラクティブな問題です。
最初に、整数 N,K,Q を標準入力から受け取ってください。
N K Q
次に、集合 \lbrace x, y \rbrace を特定できるまで質問を繰り返してください。
質問は、以下の形式で標準出力に出力してください。
? s_1s_2 \dots s_N
ここで、s_1 s_2 \dots s_N は部分集合 S を表す長さ N の文字列で、i \in S ならば s_i = {}1、i \notin S ならば s_i = {}0 としてください。
これに対する応答は、以下の形式で標準入力から与えられます。
T
ここで、T は質問に対する答えで、S の異なる 2 元の組 (i,j) であって、 i<j かつ |a_i-a_j|\leq K であるような組の個数を表します。
答えとなる集合 \lbrace x, y \rbrace を特定出来たら、特定した 2 つの要素を以下の形式で出力してください。(順番はどちらが先でも構いません。)その後、ただちにプログラムを終了してください。
! x y
注意点
- 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
- 質問の形式が間違っている場合、および、質問回数を超過した場合、ジャッジの応答は T = -1 となります。これを受け取った場合、ただちにプログラムを終了してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
- 余計な改行は不正なフォーマットの出力とみなされることに注意してください。
入出力例
以下は N = 5, K = 2, Q = 90 の場合の入出力例です。この例は入力の制約を満たさないので、テストケースには含まれないことに注意してください。
| 入力 | 出力 | 説明 |
|---|---|---|
| ジャッジは順列 (3, 5, 2, 1, 4) を隠し持っています。 | ||
5 2 90 |
まず整数 N,K,Q が与えられます。 | |
? 11000 |
S = \lbrace 1, 2 \rbrace として質問を行います。 | |
1 |
組 (1, 2) のみが条件を満たすので、標準入力に 1 が与えられます。 |
|
? 10011 |
S = \lbrace 1, 4, 5 \rbrace として質問を行います。 | |
2 |
(1, 4) と (1, 5) の 2 組が条件を満たすので、標準入力に 2 が与えられます。 |
|
! 2 4 |
答えとして \lbrace 2, 4 \rbrace を出力します。a_4 = 1 かつ a_2 = N であるので、この出力は正解です。 |
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given positive integers H and W. You aim to draw an H-row by W-column grid on the coordinate plane using several "U-shapes."
To draw one U-shape, perform the following operation:
- Choose integers 1 \le x \le H and 1 \le y \le W.
- From the following four line segments, select any three distinct ones:
- The line segment connecting (x-1, y-1) and (x-1, y)
- The line segment connecting (x-1, y-1) and (x, y-1)
- The line segment connecting (x, y) and (x-1, y)
- The line segment connecting (x, y) and (x, y-1)
- Draw the selected three line segments on the coordinate plane.
However, the line segments you draw must not share any points (other than endpoints) with any line segments drawn previously.
Is it possible to draw all the length-1 line segments connecting grid points with 0 \le x \le H and 0 \le y \le W by repeating this operation? If possible, provide an example.
Constraints
- All input values are integers.
- 1 \le H, W \le 1000
Partial Score
10 points will be awarded for passing the testset satisfying the additional constraint H,W\le 5.
Input
The input is given from Standard Input in the following format:
H W
Output
If it is impossible to draw the grid by repeating the operation, output No.
If it is possible, output such an operation sequence in the following format:
Yes S_1 \vdots S_H
Here, S_1, \dots, S_H are strings of length W, and the j-th character of S_i (1 \le i \le H, 1 \le j \le W) is defined as follows:
- If there is no operation with (x, y) = (i, j), the j-th character of S_i is
.. - Otherwise, there is exactly one operation with (x, y) = (i, j). In that operation:
- If the three selected line segments are those excluding "the line segment connecting (x-1, y-1) and (x-1, y)," then the j-th character of S_i is
v. - If the three selected line segments are those excluding "the line segment connecting (x-1, y-1) and (x, y-1)," then the j-th character of S_i is
>. - If the three selected line segments are those excluding "the line segment connecting (x, y) and (x-1, y)," then the j-th character of S_i is
<. - If the three selected line segments are those excluding "the line segment connecting (x, y) and (x, y-1)," then the j-th character of S_i is
^.
- If the three selected line segments are those excluding "the line segment connecting (x-1, y-1) and (x-1, y)," then the j-th character of S_i is
Note that the judge is case-insensitive for Yes and No.
Refer to the sample inputs and the visualizer for further clarification.
Visualizer
You can use the visualizer via the following link:
https://img.atcoder.jp/ttpc2024_1/grid_construction_visualizer_9cdb863ae8b195d0a47d8d6e2c9e05cd.html
Sample Input 1
3 3
Sample Output 1
Yes <<^ v.^ v>>
As shown in the figure, you can draw a 3 \times 3 grid by drawing U-shapes. Note that no U-shape is drawn at the location corresponding to the center cell. (For clarity, the U-shapes are colored, but this is irrelevant to the problem.)
Sample Input 2
4 4
Sample Output 2
No
Sample Input 3
4 5
Sample Output 3
No
配点 : 100 点
問題文
正整数 H,W が与えられます。あなたは座標平面にいくつかの「コの字」を用いて H 行 W 列のグリッドを描こうとしています。
1 つのコの字を描くには、次の操作を行います。
- 1\le x\le H, 1\le y\le W なる整数 x,y を選ぶ。
- 次の 4 本の線分のうち、異なる 3 本を選ぶ。
- (x-1,y-1) と (x-1,y) を端点に持つ線分
- (x-1,y-1) と (x,y-1) を端点に持つ線分
- (x,y) と (x-1,y) を端点に持つ線分
- (x,y) と (x,y-1) を端点に持つ線分
- 選んだ 3 本の線分を座標平面に描く。
ただし、描いた線分は、それまでに描いた線分と端点以外で共有点を持ってはいけません。
0 \le x \le H, 0 \le y \le W の範囲にある格子点同士を結ぶ長さ 1 の線分すべてを、この操作を繰り返すことで描くことは可能でしょうか?可能である場合は一例を示してください。
制約
- 入力はすべて整数
- 1\le H,W\le 1000
部分点
追加の制約 H, W \le 5 を満たすデータセットに正解した場合は 10 点が与えられる。
入力
入力は以下の形式で与えられる。
H W
出力
操作を繰り返してグリッドを描くことが不可能である場合は、No を出力せよ。
操作を繰り返してグリッドを描くことが可能である場合は、そのような操作列を以下の形式で出力せよ。
Yes S_1 \vdots S_H
ここで、S_1, \dots, S_H はそれぞれ長さ W の文字列であり、S_i の j 文字目 (1 ≤ i ≤ H,\ 1 ≤ j ≤ W) は次のように定義される。
- (x, y) = (i, j) であるような操作が存在しない場合、S_i の j 文字目は
.である。 - そうでない場合、(x, y) = (i, j) であるような操作はちょうど 1 回存在する。その操作において、
- 「(x-1,y-1) と (x-1,y) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
vである。 - 「(x-1,y-1) と (x,y-1) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
>である。 - 「(x,y) と (x-1,y) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
<である。 - 「(x,y) と (x,y-1) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
^である。
- 「(x-1,y-1) と (x-1,y) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
なお、ジャッジは Yes と No の大文字・小文字を区別しない。
入出力例やビジュアライザも参考にせよ。
ビジュアライザ
以下のリンクからビジュアライザを利用できます。
https://img.atcoder.jp/ttpc2024_1/grid_construction_visualizer_9cdb863ae8b195d0a47d8d6e2c9e05cd.html
入力例 1
3 3
出力例 1
Yes <<^ v.^ v>>
図のようにコの字を描くことで、 3 \times 3 のグリッドを描くことができます。中央のマスに対応する場所にはコの字を描いていないことに注意してください。(見やすさのため、コの字に色をつけていますが、問題には関係ありません。)
入力例 2
4 4
出力例 2
No
入力例 3
4 5
出力例 3
No
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given a sequence A = (A_1, A_2, \dots, A_N) of length N consisting of 0s and 1s. Define a simple undirected graph G = (V, E) with \frac{N (N - 1)}{2} vertices as follows:
- For every pair of integers (i, j) satisfying 1 \leq i < j \leq N, (i, j) \in V. This vertex is called vertex (i, j).
- For every triple of integers (i, j, k) satisfying 1 \leq i < j < k \leq N and A_i + A_j + A_k = 1, there is an edge connecting vertex (i, j) and vertex (j, k).
- No other pairs of vertices have edges.
Determine the number of connected components in G.
You are given T test cases. For each test case, compute the answer.
Constraints
- All input values are integers.
- 1 \leq T \leq 10^5
- 3 \leq N \leq 10^6
- A_i is 0 or 1 (1 \leq i \leq N)
- The total sum of N over all test cases in a single input is at most 10^6.
Partial Score
30 points will be awarded for passing the test set satisfying the following constraints:
- 1 \leq T \leq 1000
- 3 \leq N \leq 5000
- The total sum of N over all test cases in a single input is at most 5000.
Input
The input is given in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Here, \text{case}_i represents the i-th test case. Each test case is given in the following format:
N A_1 A_2 \cdots A_N
Output
For each test case, output the answer.
Sample Input 1
4 5 1 0 0 1 0 5 1 1 1 1 1 12 0 0 1 1 1 0 0 0 1 0 1 0 20 0 0 1 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0 1 1
Sample Output 1
4 10 13 58
For the first test case, the connected components are as follows:
- \lbrace (1,2),(2,3),(2,4),(2,5),(3,4),(4,5) \rbrace
- \lbrace (1,3),(3,5) \rbrace
- \lbrace (1,4) \rbrace
- \lbrace (1,5) \rbrace
For the second test case, the graph has no edges, so the number of connected components is 10.
配点 : 100 点
問題文
0 と 1 からなる長さ N の数列 A = (A_1, A_2, \dots, A_N) が与えられます。\frac{N (N - 1)}{2} 頂点の単純無向グラフ G = (V, E) を以下のように定義します。
- 1 ≤ i < j ≤ N を満たす任意の整数の組 (i, j) に対して、(i, j) \in V である。この頂点を頂点 (i, j) と呼ぶ。
- 1 ≤ i < j < k ≤ N かつ A_i + A_j + A_k = 1 を満たす任意の整数の組 (i, j, k) に対して、頂点 (i, j) と頂点 (j, k) を結ぶ辺が存在する。
- これ以外の頂点の組には辺が存在しない。
G の連結成分の個数を求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 入力はすべて整数
- 1 \leq T \leq {10}^5
- 3 \leq N \leq {10}^6
- A_i は 0 または 1 (1 \leq i \leq N)
- 1 つの入力の中のテストケースすべてにわたる N の総和は {10}^6 以下
部分点
以下の制約を満たすデータセットに正解した場合は 30 点が与えられる。
- 1 \leq T \leq 1000
- 3 \leq N \leq 5000
- 1 つの入力の中のテストケースすべてにわたる N の総和は 5000 以下
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
ここで、\text{case}_i は i 番目のテストケースを表す。各テストケースは以下の形式で与えられる。
N A_1 A_2 \cdots A_N
出力
各テストケースに対し、答えを出力せよ。
入力例 1
4 5 1 0 0 1 0 5 1 1 1 1 1 12 0 0 1 1 1 0 0 0 1 0 1 0 20 0 0 1 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0 1 1
出力例 1
4 10 13 58
1 個目のテストケースについて、連結成分は以下の 4 つです。
- \lbrace (1,2),(2,3),(2,4),(2,5),(3,4),(4,5) \rbrace
- \lbrace (1,3),(3,5) \rbrace
- \lbrace (1,4) \rbrace
- \lbrace (1,5) \rbrace
2 個目のテストケースについて、グラフに辺は張られないため連結成分の個数は 10 です。
実行時間制限: 2 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
In this problem, when we refer to a "permutation of length K", we mean a permutation of (0, 1, \dots, K - 1). Also, we denote the k-th element (0-based) of a sequence X as X[k].
You are given a permutation P of length L, and L permutations of length B, denoted as V_{0}, V_{1}, \dots, V_{L - 1}.
We define a sequence A of length B^L as follows:
For each 0 ≤ n < B^L, when n is represented as an L-digit number in base B, let N[i] be the value at the B^i place (0 ≤ i < L). Then,\displaystyle A[n] = \sum_{i=0}^{L-1} V_i[N[i]] \cdot B^{P[i]}
Find the inversion number of the sequence A modulo 998244353.
Constraints
- All input values are integers
- 1 \leq L
- 2 \leq B
- L \times (B + 1) \leq 5 \times 10^{5}
- P is a permutation of length L
- For each 0 \leq i < L, V_{i} is a permutation of length B
Input
Input is given from standard input in the following format:
L B
P[0] P[1] \cdots P[L - 1]
V_{0}[0] V_{0}[1] \cdots V_{0}[B - 1]
\vdots
V_{L - 1}[0] V_{L - 1}[1] \cdots V_{L - 1}[B - 1]
Output
Print the answer.
Sample Input 1
3 2 2 0 1 1 0 1 0 0 1
Sample Output 1
14
For example, when n = 5, since N = (1, 0, 1), we have A[5] = V_{0}[1] \cdot 2^{P[0]} + V_{1}[0] \cdot 2^{P[1]} + V_{2}[1] \cdot 2^{P[2]}=3.
By calculating similarly, we get A = (5, 1, 4, 0, 7, 3, 6, 2). The inversion count of A is 14, so output 14.
Sample Input 2
2 4 1 0 2 0 3 1 1 2 3 0
Sample Output 2
60
A = (9, 1, 13, 5, 10, 2, 14, 6, 11, 3, 15, 7, 8, 0, 12, 4). The inversion count of A is 60, so output 60.
Sample Input 3
9 10 2 5 7 3 8 1 4 6 0 9 2 4 0 1 6 7 3 5 8 4 1 6 7 8 0 5 9 2 3 1 9 2 4 6 8 5 7 0 3 9 0 8 2 5 1 6 7 3 4 1 6 0 7 3 9 2 4 5 8 4 5 2 9 1 6 7 3 0 8 7 0 5 6 1 9 2 4 3 8 3 2 1 6 7 0 8 9 4 5 9 2 4 3 5 8 0 6 7 1
Sample Output 3
138876070
Output the answer modulo 998244353.
配点 : 100 点
問題文
この問題で「長さ K の順列」と言った際は「(0, 1, \dots, K - 1) の順列」を指すものとします。また、数列 X の k 番目の要素(最初の要素を 0 番目とする)を X[k] と表すこととします。
長さ L の順列 P と、L 個の長さ B の順列 V_{0}, V_{1}, \dots, V_{L - 1} が与えられます。
長さ B^L の数列 A を以下のように定義します。
各 0 ≤ n < B^L に対し、n を B 進 L 桁で表した際の B^i の位 (0 ≤ i < L) の値を N[i] とすると、\displaystyle A[n] = \sum_{i=0}^{L-1} V_i[N[i]] \cdot B^{P[i]}である。
数列 A の転倒数を 998244353 で割ったあまりを求めてください。
制約
- 入力はすべて整数
- 1 \leq L
- 2 \leq B
- L \times (B + 1) \leq 5 \times 10^{5}
- P は長さ L の順列である
- 各 0 \leq i < L について、V_{i} は長さ B の順列である
入力
入力は以下の形式で標準入力から与えられる。
L B
P[0] P[1] \cdots P[L - 1]
V_{0}[0] V_{0}[1] \cdots V_{0}[B - 1]
\vdots
V_{L - 1}[0] V_{L - 1}[1] \cdots V_{L - 1}[B - 1]
出力
答えを出力せよ。
入力例 1
3 2 2 0 1 1 0 1 0 0 1
出力例 1
14
例えば n = 5 のとき、N = (1, 0, 1) であるので、A[5] = V_{0}[1] \cdot 2^{P[0]} + V_{1}[0] \cdot 2^{P[1]} + V_{2}[1] \cdot 2^{P[2]}=3 です。
同様にして計算すると、A = (5, 1, 4, 0, 7, 3, 6, 2) となります。A の転倒数は 14 であるので、14 を出力します。
入力例 2
2 4 1 0 2 0 3 1 1 2 3 0
出力例 2
60
A = (9, 1, 13, 5, 10, 2, 14, 6, 11, 3, 15, 7, 8, 0, 12, 4) です。A の転倒数は 60 であるので、60 を出力します。
入力例 3
9 10 2 5 7 3 8 1 4 6 0 9 2 4 0 1 6 7 3 5 8 4 1 6 7 8 0 5 9 2 3 1 9 2 4 6 8 5 7 0 3 9 0 8 2 5 1 6 7 3 4 1 6 0 7 3 9 2 4 5 8 4 5 2 9 1 6 7 3 0 8 7 0 5 6 1 9 2 4 3 8 3 2 1 6 7 0 8 9 4 5 9 2 4 3 5 8 0 6 7 1
出力例 3
138876070
998244353 で割ったあまりを求めてください。
実行時間制限: 3 sec / メモリ制限: 1024 MiB
Score: 100 points
Problem Statement
You are given a permutation A = (A_1, A_2, \dots, A_N) of (1, 2, \dots, N).
For a pair of integers l, r (1 \le l \le r \le N), we define the Cartesian Tree \text{C}(l, r) as follows:
- \text{C}(l, r) is a rooted binary tree with r - l + 1 nodes. We denote the root of this tree as \mathit{rt}.
- Let m be the unique integer such that A_m = \min\lbrace A_l, A_{l+1}, \dots, A_r\rbrace.
- If l < m, then the left subtree of \mathit{rt} is \text{C}(l, m-1). If l = m, then \mathit{rt} has no left child.
- If m < r, then the right subtree of \mathit{rt} is \text{C}(m+1, r). If m = r, then \mathit{rt} has no right child.
You are given Q pairs of integers (l_1, r_1), (l_2, r_2), \dots, (l_Q, r_Q). Determine how many different Cartesian Trees are there among \text{C}(l_1, r_1), \text{C}(l_2, r_2), \dots, \text{C}(l_Q, r_Q).
Two Cartesian Trees X and Y are considered the same if and only if all of the following conditions are satisfied:
Let the root of X be \mathit{rt}_X, and the root of Y be \mathit{rt}_Y.
- If \mathit{rt}_X has a left child, then \mathit{rt}_Y also has a left child and the left subtrees of \mathit{rt}_X and \mathit{rt}_Y are the same Cartesian Tree.
- If \mathit{rt}_X has no left child, then \mathit{rt}_Y also has no left child.
- If \mathit{rt}_X has a right child, then \mathit{rt}_Y also has a right child and the right subtrees of \mathit{rt}_X and \mathit{rt}_Y are the same Cartesian Tree.
- If \mathit{rt}_X has no right child, then \mathit{rt}_Y also has no right child.
Constraints
- All input values are integers.
- 1 \le N \le 4 \times 10^5
- A is a permutation of (1, 2, \dots, N).
- 1 \le Q \le 4 \times 10^5
- 1 \le l_i \le r_i \le N (1 \le i \le Q)
- (l_i, r_i) \ne (l_j, r_j) (1 \le i < j \le Q)
Input
The input is given in the following format:
N A_1 A_2 \ldots A_N Q l_1 r_1 l_2 r_2 \vdots l_Q r_Q
Output
Print the answer.
Sample Input 1
6 1 4 2 6 3 5 3 1 4 2 5 3 6
Sample Output 1
2
\text{C}(1, 4), \text{C}(2, 5), \text{C}(3, 6) are the following Cartesian Trees:
\text{C}(1, 4) and \text{C}(3, 6) are the same Cartesian Tree, while \text{C}(2, 5) is a different Cartesian Tree from these. Therefore, there are 2 different Cartesian Trees.
Sample Input 2
4 1 2 3 4 10 1 1 2 2 3 3 4 4 1 2 2 3 3 4 1 3 2 4 1 4
Sample Output 2
4
Sample Input 3
10 3 8 4 7 2 5 9 10 1 6 13 5 8 2 6 7 9 3 8 3 5 2 4 4 6 1 9 3 7 6 9 2 10 4 9 3 9
Sample Output 3
11
配点 : 100 点
問題文
(1, 2, \dots, N) の順列 A = (A_1, A_2, \dots, A_N) が与えられます。
整数の組 l, r (1 \le l \le r \le N) に対し、Cartesian Tree \text{C}(l, r) を以下のように定義します。
- \text{C}(l, r) は r-l+1 頂点の根付きの二分木である。この木の根を \mathit{rt} と書くことにする。
- 整数 m を、A_m = \min\lbrace A_l, A_{l+1}, \dots, A_r\rbrace を満たす唯一の整数とする。
- l < m のとき、\mathit{rt} の左部分木は \text{C}(l, m-1) である。l = m のとき、\mathit{rt} に左の子は存在しない。
- m < r のとき、\mathit{rt} の右部分木は \text{C}(m+1, r) である。m = r のとき、\mathit{rt} に右の子は存在しない。
Q 組の整数 (l_1, r_1), (l_2, r_2), \dots, (l_Q, r_Q) が与えられます。\text{C}(l_1, r_1), \text{C}(l_2, r_2), \dots, \text{C}(l_Q, r_Q) の中に Cartesian Tree が何種類あるかを求めてください。
ただし、2 つの Cartesian Tree X, Y は、以下の条件をすべて満たすとき、かつそのときに限り同じ Cartesian Tree であると見なされます。
X の根を \mathit{rt}_X と書き、Y の根を \mathit{rt}_Y と書くことにする。
- \mathit{rt}_X に左の子が存在するならば、\mathit{rt}_Y にも左の子が存在し、「\mathit{rt}_X の左部分木」と「\mathit{rt}_Y の左部分木」は同じ Cartesian Tree である。
- \mathit{rt}_X に左の子が存在しないならば、\mathit{rt}_Y の左の子も存在しない。
- \mathit{rt}_X に右の子が存在するならば、\mathit{rt}_Y にも右の子が存在し、「\mathit{rt}_X の右部分木」と「\mathit{rt}_Y の右部分木」は同じ Cartesian Tree である。
- \mathit{rt}_X に右の子が存在しないならば、\mathit{rt}_Y の右の子も存在しない。
制約
- 入力はすべて整数
- 1 \le N \le 4 \times 10^5
- A は (1, 2, \dots, N) の順列である。
- 1 \le Q \le 4 \times 10^5
- 1 \le l_i \le r_i \le N (1 \le i \le Q)
- (l_i, r_i) \ne (l_j, r_j) (1 \le i < j \le Q)
入力
入力は以下の形式で与えられる。
N A_1 A_2 \ldots A_N Q l_1 r_1 l_2 r_2 \vdots l_Q r_Q
出力
答えを出力せよ。
入力例 1
6 1 4 2 6 3 5 3 1 4 2 5 3 6
出力例 1
2
\text{C}(1, 4), \text{C}(2, 5), \text{C}(3, 6) はそれぞれ以下のような Cartesian Tree です。
\text{C}(1, 4) と \text{C}(3, 6) は同じ Cartesian Tree で、\text{C}(2, 5) はこれらとは異なる Cartesian Tree です。したがって、Cartesian Tree は 2 種類存在します。
入力例 2
4 1 2 3 4 10 1 1 2 2 3 3 4 4 1 2 2 3 3 4 1 3 2 4 1 4
出力例 2
4
入力例 3
10 3 8 4 7 2 5 9 10 1 6 13 5 8 2 6 7 9 3 8 3 5 2 4 4 6 1 9 3 7 6 9 2 10 4 9 3 9
出力例 3
11

