NUPC 2024

A - Equalization

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 個の整数からなる数列 A = (A_1, A_2, \dots, A_N) が与えられます。あなたは以下の操作を好きな回数行うことができます。

1 \leq i \leq N-1 を満たす整数 i を選び、 A_i から 1 を引いて A_{i+1} に 1 を足す。

数列 A のすべての値を等しくするために必要な最小の操作回数を求めてください。ただし、不可能な場合は -1 を出力してください。

制約

1 \leq N \leq 2 \times 10^5
1 \leq A_i \leq 10^9 (1 \leq i \leq N)
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

N
A_1 A_2 \dots A_N

出力

標準出力へ答えを一行で出力してください。

入力例1

4
7 4 5 4

出力例1

i=2,1,3,1 の順に操作を行うと、 A のすべての値が等しくなります。 3 回以下の操作では A のすべての値を等しくすることはできないため、 4 を出力します。

入力例2

5
7 8 3 5 5

出力例2

-1

どのように操作を行ってもすべての値を等しくできないときは、 -1 を出力します。

B - おつり

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

NUPC国では現在 N 種類の硬貨が流通しており、それぞれの価値は C_1, C_2, \dots, C_N 円です。

あなたはこれらの硬貨をそれぞれ順に A_1, A_2, \dots, A_N 枚ずつ持っています。

あなたは M 円の商品を購入したいと考えています。店側はすべての硬貨をそれぞれ 10^{100} 枚ずつ持っており、M 円を超えて支払った場合、おつりは硬貨の枚数が最小となるように支払われます。（本問題の制約下では、このような支払い方は一意に定まります。）

また、支払いに使った硬貨がおつりとして返ってくるような支払い方はできません。 たとえば、10 円の硬貨を支払いに使い、おつりにも 10 円の硬貨が含まれるような支払い方はできません。

あなたは、商品の購入後に手元に残る硬貨の枚数を最小化したいと考えています。手元に残る硬貨の枚数が最小となる支払い方の一例を出力してください。

制約

入力はすべて整数
1\leq N\leq 30
1=C_1<C_2<\cdots<C_N\leq 10^9
C_{i+1} は C_{i} の倍数である (1\leq i\leq N-1)
0\leq A_i\leq 10^9 (1\leq i\leq N)
1\leq M\leq \sum_{i=1}^N {C_i \cdot A_i}

入力

入力は以下の形式で標準入力から与えられます。

N M
C_1 C_2 \dots C_N
A_1 A_2 \dots A_N

出力

支払い方の一例を次のように出力してください。

m_1 m_2 \dots m_N

ここで m_1, m_2, \dots, m_N は各硬貨を支払う枚数であり、 0\le m_i \le A_i (1\le i \le N) かつ \sum_{i=1}^N C_i \cdot m_i \geq M を満たす必要があります。

入力例1

6 100
1 5 10 50 100 500
1 1 1 1 1 1

出力例1

0 0 0 0 1 0

100 円の硬貨を 1 枚使うと、最終的に所持する硬貨の枚数は 5 枚となります。4 枚以下となる支払い方はできないので、これが答えの一例となります。

入力例2

6 100
1 5 10 50 100 500
2 2 2 2 2 2

出力例2

0 2 0 2 0 0

50 円の硬貨を 2 枚、5 円の硬貨を 2 枚使うと、最終的に所持する硬貨の枚数は 9 枚となります。8 枚以下となる支払い方はできないので、これが答えの一例となります。

また、以下の支払い方でも 9 枚は達成できますが、10 円の硬貨を支払いに使い、おつりでも受け取るので、支払い方の条件を満たしません。

0 2 1 2 0 0

入力例3

4 1000
1 100 500 1000
2000 0 0 0

出力例3

2000 0 0 0

C - Median of Medians

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

奇数 N, M が与えられます。整数の集合 \{1,2,\dots,NM\} の「要素数 M 個ずつの N 個のグループ」への分割に対して、以下の「中央値の中央値」を定めます。

各グループ内の中央値（昇順で (M+1)/2 番目の値）を求める。
手順１で得た N 個の値の中央値を「中央値の中央値」とする。

各 k \in \{1,2,\dots,NM\} について、「中央値の中央値」が k となる分割方法の数を \text{mod }998244353 で出力してください。ただし、二つの分割方法について、「一方の分割では同じグループに含まれ、もう一方では異なるグループに含まれる異なる整数の組」が存在するとき、またそのときに限りそれらを区別するものとします。

制約

入力はすべて整数
1 \le N,M \le 999
N,M は奇数

入力

入力は以下の形式で標準入力から与えられます。

N M

出力

NM 行出力してください。 i 行目には、「中央値の中央値」が i となる分割方法の数を \text{mod }998244353 で出力してください。

入力例 1

3 3

出力例 1

入力例 2

1 3

出力例 2

0
1
0

入力例 3

5 5

出力例 3

\text{mod }998244353 で出力してください。

D - Painting

Time Limit: 3 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

H 行 W 列のグリッドがあり、はじめすべてのマスは無色です。グリッドの上から i 行目、左から j 列目のマスを (i,j) と表します。また黒と異なる N 種類の色 1, \dots, N があります。

Q 個のクエリが与えられるので順に処理し、グリッドの各マスの色を出力してください。クエリは 3 種類あり、以下のいずれかの形式で与えられます。

1 i l r: マス (i,l),(i,l+1),\dots,(i,r) を黒で塗る
2 j u d: マス (u,j),(u+1,j),\dots,(d,j) を黒で塗る
3 i j c: マス (i,j) に連結なマスをすべて色 c で塗る

ただし 2 つのマス S,T が連結であるとは、 S,T が両方黒でなく、上下左右に隣り合う黒でないマスへの移動を繰り返して S から T へ移動できることをいいます。

制約

1\leq H, W
1\leq H\times W\leq 2\times10^5
1\leq N,Q\leq 2\times10^5
1 つめの形式のクエリにおいて、1\leq i\leq H,\ 1\leq l\leq r\leq W
2 つめの形式のクエリにおいて、1\leq j\leq W,\ 1\leq u\leq d\leq H
3 つめの形式のクエリにおいて、1\leq i\leq H,\ 1\leq j\leq W,\ 1\leq c\leq N
3 つめの形式のクエリにおいて、クエリを処理する前の時点でマス (i,j) は黒でない
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

H W
N Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q

各クエリは以下の 3 種類のいずれかの形式で与えられます。

1 i l r

2 j l r

3 i j c

出力

すべてのクエリを処理した後のグリッドの状態を、以下の形式で標準出力に出力してください。

c_{1,1}\  c_{1,2}\  \dots \ c_{1,W}
c_{2,1}\  c_{2,2}\  \dots \ c_{2,W}
\vdots
c_{H,1}\  c_{H,2}\  \dots \ c_{H,W}

c_{i,j} はマス (i,j) の色を表します。ただしマス (i,j) が黒色である場合は 0、無色である場合は -1 としてください。

入力例1

出力例1

2 2 2
0 0 0
1 1 1

各クエリを処理した後のグリッドの状態は以下の図のようになります。

1 つ目のクエリでは、すべてのマスが連結なので、すべてのマスが色 1 で塗られます。 2 つ目のクエリでは、2 行目のマスすべてが黒色で塗られます。 3 つ目のクエリでは、1 行目のマスすべてが色 2 で塗られます。

入力例2

出力例2

-1 0 4 4 0 3
0 0 0 4 0 3
1 0 4 4 0 3
1 0 0 0 0 0
1 0 2 2 2 2

E - Exponential

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

長さ N の整数列 A = (A_1, A_2, \dots, A_N) と整数 M が与えられます。
以下の条件をすべて満たす整数の組 (i,j,k) の個数を求めてください。

1\leq i,j,k \leq N
i, j, k は全て異なる
A_i \times M^{A_j}=A_k

制約

3\leq N\leq 2\times10^5
1\leq M\leq 10^{18}
0\leq A_i\leq10^{18}
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

N M
A_1 A_2 \dots A_N

出力

答えを出力せよ。

入力例 1

5 2
1 2 4 8 16

出力例 1

条件を満たす (i, j, k) の組合せは以下の 6 通りです。

(1, 2, 3)
(1, 3, 5)
(2, 1, 3)
(3, 1, 4)
(3, 2, 5)
(4, 1, 5)

入力例 2

8 3
0 3 2 6 18 1 2 0

出力例 2

入力例 3

12 1
0 0 0 0 0 0 0 1 1 1 1 1

出力例 3

F - Labeled Tree Distance

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 頂点の木 T が与えられます。辺 i は頂点 u_i と v_i を結んでいます。最初、頂点 i は色 A_i で塗られています。 Q 個のクエリが与えられるので、順番に処理してください。クエリは次の 2 種類のいずれかです。

1 k x: 頂点 k を色 x で塗る
2 y: 色 y で塗られている 2 頂点の距離の最大値を出力する

ここで、2 頂点 (u,v) の距離とは、u と v を両端点とするパスに含まれる辺の本数です。

制約

2 \le N \le 10^5
1 \le u_i,v_i \le N
1 \le A_i \le N
1 \le Q \le 10^5
1 \le k \le N
1 \le x \le N
1 \le y \le N
クエリ2 yが与えられるとき、色 y で塗られている頂点が 2 つ以上存在する
入力は全て整数である
与えられるグラフは木である

入力

入力は以下の形式で標準入力から与えられます。

N
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
A_1\  A_2\  \ldots\  A_N
Q
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q

ここで、\mathrm{query}_i は i 個目のクエリであり、以下のいずれかの形式で与えられます。

1 k x

2 y

出力

2番目の形式のクエリの回数を q として q 行出力してください。 j (1\leq j \leq q) 行目では 2 番目の形式のクエリのうち j 個目のものに対する答えを出力してください。

入力例 1

出力例 1

2
1

最初、全てのマスが色 1 で塗られています。このとき、色 1 で塗られている 2 頂点のうち、頂点 1 と頂点 3 の距離が最大となり、その距離は 2 です。その後、頂点 1 が色 2 で塗られると、色 1 で塗られている頂点では頂点 2 と頂点 3 の距離である 1 が最大となります。

入力例 2

出力例 2

1
2
1

入力例 3

6
1 2
2 3
3 4
4 5
4 6
1 3 2 1 1 3
6
2 1
1 2 3
1 1 2
1 6 4
2 1
2 2

出力例 3

4
1
2

G - Super 累積 XOR

Time Limit: 4 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 個の整数からなる数列 A = (A_1, A_2, \dots, A_N) が与えられます。

以下の操作を K 回行った後の A を出力してください。

i=1,2, \dots ,N に対して一斉に A_i を A_1 \oplus A_2 \oplus \dots \oplus A_i に置き換える。

ただし、 \oplus はビットごとの排他的論理和を表します。

制約

1 \le N \le 2 \times 10^5
1 \le K \le 10^{18}
0 \le A_i < 2^{30}
入力はすべて整数

部分点

追加の制約 N \le 1000 を満たすデータセットに正解した場合は 1 点が与えられる。

入力

入力は以下の形式で標準入力から与えられます。

N K
A_1 A_2 \dots A_N

出力

上述の操作を K 回行った後の A=(A_1,A_2,\dots,A_N) の各要素を、順に空白区切りで出力してください。

入力例 1

3 2
1 2 3

出力例 1

1 2 2

はじめ、 (A_1, A_2, A_3)=(1,2,3) です。

1 回目の操作を行うと (A_1, A_2, A_3)=(1,1 \oplus 2,1 \oplus 2 \oplus 3)=(1,3,0) となります。

2 回目の操作を行うと (A_1, A_2, A_3)=(1,1 \oplus 3,1 \oplus 3 \oplus 0)=(1,2,2) となります。

入力例 2

10 3141592653589793
528994566 21013803 220742658 357578426 605624719 350507118 731879815 393165536 215218511 161335641

出力例 2

528994566 516387885 334442543 113182357 581312282 910315380 501077747 179498003 107025756 268229637

H - LCS order

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

長さ N の文字列 S と、長さ M の文字列 T が与えられます。

以下の Q 個のクエリに答えてください。

i \ (1\leq i\leq Q) 番目のクエリは以下の通りです。

S, T の LCS のうち、辞書順で k_i 番目のものを出力する。

ただし、該当する LCS が存在しない場合や空文字列である場合は、-1 を出力してください。

なお、LCS 同士が文字列として等しい場合、異なる位置から取り出したものであっても、それらは区別しないものとします。

LCS (最長共通部分列)とは

文字列 S, T の LCS とは、S の部分列でも T の部分列でもあるような文字列のうち、長さが最大のもののことを指します。ここで、ある文字列 U の部分列とは、U から 0 個以上の文字を取り出し、それらを順序を変えずに並べた文字列のことを指します。

制約

1\leq N,M,Q\leq 1000
1\leq k_i\leq 10^9
N,M,Q,k_i は整数
S は長さ N の英小文字列
T は長さ M の英小文字列

入力

入力は以下の形式で標準入力から与えられます。

N M
S
T
Q
k_1
k_2
\vdots
k_Q

出力

Q 行出力してください。

i \ (1\leq i\leq Q) 行目には、i 番目のクエリの答えを出力してください。

入力例1

6 6
abcdef
abfedc
4
1
2
4
8

出力例1

abc
abd
abf
-1

LCS の長さは 3 であり、辞書順にすべて列挙すると、abc, abd, abe, abfとなります。

したがって、 3 番目のクエリまでは 1, 2, 4 番の LCS を出力します。

4 番目のクエリでは、LCS の数は全部で 4 種類であるため -1 を出力します。

入力例2

5 5
abcde
abbbb
2
1
2

出力例2

ab
-1

LCS の長さは 2 であり、辞書順にすべて列挙すると、ab のみとなります。(取る添え字が異なるものは区別しません。)

入力例3

4 4
abcd
efgh
1
1

出力例3

-1

二つの文字列で一致する箇所はなく、LCS は空文字列となるため -1 を出力します。

I - Eat and Build

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

ビーバーのメイダイ君は、木を使って K 個の家を作ろうと思っています。メイダイ君は、次のどちらかの行動を取ります。

行動 1 : 木を 1 本使って家を 1 個作る。メイダイ君の体力は 1 減る。
行動 2 : 木を 1 本食べる。メイダイ君の体力は 1 増える。

最初、メイダイ君の体力は H です。メイダイ君は体力が h のとき、\frac{h}{H} の確率で行動 1 を、\frac{H-h}{H} の確率で行動 2 をします。メイダイ君は、家を K 個作った時点で行動を終了します。また、木は無限に存在するとして、家を K 個作るまで行動を終了することはありません。

K 個の家を作るまでに行動 1 と行動 2 で消費される合計の木の本数の期待値を有理数 \bmod~998244353 で求めてください。ただし、行動 1 と行動 2 で、木はちょうど 1 本ずつ消費され、これらの行動以外で木を消費したり、体力が増えたり減ったりすることはありません。

有理数 \bmod~998244353 とは

求める期待値は必ず有理数となることが証明できます。またこの問題の制約下では、その値を互いに素な 2 つの整数 P,Q を用いて P / Q と表したとき、R \times Q \equiv P \pmod{998244353} かつ 0 \leq R < 998244353 を満たすを満たす整数 R がただ一つ存在することが証明できます。この R を求めてください。

制約

1 \leq H \leq 3\times10^3
1 \leq K \leq 3\times10^3
入力される値は全て整数

入力

入力は以下の形式で標準入力から与えられます。

H K

出力

答えを出力せよ。

入力例 1

2 2

出力例 1

499122179

最初、メイダイ君の体力は 2 です。このとき、確率 \frac{2}{2} = 1 で家を作ります。すると、メイダイ君の体力は 1 になります。次に、メイダイ君は以下の 2 通りの行動を取ります。

\frac{1}{2} の確率で行動 1 を取る。 2 個目の家を作り、メイダイ君の体力は 0 になります。
\frac{2-1}{2} = \frac{1}{2} の確率で行動 2 を取る。家の個数は 1 のままで、メイダイ君の体力は 2 になります。

1 つ目の場合は、家が合計で 2 個作られたため、行動を終了します。 2 つ目の場合は、続けて確率 1 で行動 1 を取り、2 個目の家を作って行動を終了します。

したがって、メイダイ君が家を 2 個作るまで行動するとき、\frac{2}{2} \times \frac{1}{2} = \frac{1}{2} の確率で木を 2 本消費し、\frac{2}{2} \times \frac{1}{2} \times \frac{2}{2} = \frac{1}{2} の確率で木を 3 本消費することがわかります。よって家が 2 個作られるまでに消費される木の本数の期待値は 2 \times \frac{1}{2} + 3 \times \frac{1}{2} = \frac{5}{2} であり、499122179 \times 2 \equiv 5 \pmod{998244353} なので 499122179 が答えになります。

入力例 2

3 5

出力例 2

733050045

入力例 3

10 10

出力例 3

887776226

J - Cops and Robbers on Namori

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

Alice と Bob がグラフ上のケイドロで遊ぼうとしています。

グラフ上のケイドロでは、ターン制で以下のいずれかの行動を交互に行います。

今いる頂点から、隣接頂点へ移動する。

パスする。（今いる頂点に留まる。）

Alice が行動を行った直後に Alice と Bob が同じ頂点にいるとき、Alice は Bob を捕まえることができます。

Alice と Bob が遊ぶ N 頂点 N 辺の単純無向連結グラフが与えられます。 i 番目の辺は頂点 u_i と頂点 v_i を結んでいます。

Alice と Bob がそれぞれ頂点 a, b にいる状態で、Alice のターンから始めます。有限ターン内に Alice が Bob を必ず捕まえられるか判定してください。ただし、 Alice と Bob は互いに相手の位置を知っており、 Alice は Bob をできる限り捕まえようと、 Bob は Alice にできる限り捕まらないように行動するものとします。

制約

3 \le N \le 2\times 10^5
1 \le u_i,v_i \le N
1 \le a,b \le N
a \neq b
与えられるグラフは単純である。すなわち、自己ループや多重辺は存在しない。
与えられるグラフは連結である。
入力はすべて整数。

入力

入力は以下の形式で標準入力から与えられます。

N a b
u_1 v_1
u_2 v_2
\vdots
u_N v_N

出力

有限ターン内に Alice が Bob を必ず捕まえられるときAlice、そうでないときBobを出力してください。

入力例 1

出力例 1

Alice

たとえば以下の進行が考えられます。

Alice がパスする。
Bob が頂点 5 に移動する。
Alice が頂点 6 に移動し、Bob を捕まえる。

この進行はあくまで一例ですが、この入力例では Alice が有限ターン内で Bob を必ず捕まえられることが証明できます。

入力例 2

出力例 2

Alice

入力例 3

出力例 3

Bob

K - A Shortcut

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

この問題は インタラクティブ な問題（あなたの作成したプログラムとジャッジプログラムが入出力を介して対話を行う形式の問題）です。

整数 N が与えられます。また、ジャッジは次のように構成される N 頂点の無向グラフ G を秘匿しています。

G の頂点にはそれぞれ 1, 2, \dots , N の番号が振られている。
すべての 1 \le i < N を満たす整数 i に対して、頂点 i と頂点 i+1 の間に辺が存在する。
y - x > 1 かつ 1 \le x, y \le N を満たす整数の組 (x, y) が ただ 1 つ 存在し、頂点 x と頂点 y の間に辺が存在する。
上記の N 本の辺の他に辺はない。

あなたは、 G について以下のクエリを送ることができます。

2 つの頂点番号 p, q を選ぶ。頂点 p から頂点 q への最短経路の長さ（経路上の辺の数）を質問する。

\lceil \log_2 N + 1 \rceil 回以内のクエリで (x, y) を特定してください。

なお、ジャッジは適応的 (adaptive) ではなく、各テストケースに対して固定された (x, y) を持っています。

テストケースが T 個与えられるので、それぞれについて (x, y) を特定してください。

制約

1\leq T\leq 10^3
3\leq N\leq 10^9
1 \le x < y \le N
y - x > 1
T, N, x, y は整数

入出力

最初に、標準入力に整数 T が与えられます。

次に、 T 個のテストケースが与えられます。各テストケースは次の形式で与えられます。

まず、整数 N が与えられます。

次に、 \lceil \log_2 N +1 \rceil 回までクエリを行うことができます。
各クエリは以下の形式で標準出力に出力してください。ここで、p, q は 1 \le p, q \le N を満たす整数である必要があります。

? p q

これに対する応答は、次の形式で標準入力から与えられます。

\mathrm{dist}(p, q)

ここで、 \mathrm{dist}(p, q) は頂点 p から頂点 q までの最短経路の長さを表します。ただし、不正なクエリを行った場合、またはクエリ回数が \lceil \log_2 N + 1 \rceil 回を超えた場合、ジャッジは -1 を出力します。

ジャッジが -1 を出力した場合、残りのテストケースに関わらずプログラムはすでに不正解とみなされています。この場合、ただちにプログラムを終了してください。

(x, y) を回答する場合、次の形式で標準出力に出力してください。この出力はクエリ回数に含まれません。

! x y

その後、次のテストケースが存在する場合は、次のテストケースに引き続き回答してください。最後のテストケースに回答した後は、プログラムを終了してください。

注意点

出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
不正な出力や動作に対するジャッジは不定である可能性があります。
(x, y) は対話の前に固定されており、対話内容によって変化することはありません。

入出力例

入力	出力	説明
`2`		まず整数 `T` が与えられます。
`10`		`1` つ目のテストケースが始まりました。各テストケースでは、まず整数 `N` が与えられます。
	`? 1 10`	`p = 1, q = 10` として質問を行います。
`6`		`\mathrm{dist}(1, 10)=6` が与えられます。
	`? 8 6`	`p = 8, q = 6` として質問を行います。
`2`		`\mathrm{dist}(8, 6)=2` が与えられます。
	`? 3 7`	`p = 3, q = 7` として質問を行います。
`1`		`\mathrm{dist}(3, 7)=1` が与えられます。
	`! 3 7`	答えとして `(x, y) = (3, 7)` を出力します。この出力は正解です。
`3`		`2` つ目のテストケースが始まりました。まず整数 `N` が与えられます。
	`? 1 2`	`p = 1, q = 2` として質問を行います。
`1`		`\mathrm{dist}(1, 2)=1` が与えられます。
	`! 1 3`	答えとして `(x, y) = (1, 3)` を出力します。この出力は正解です。テストケースは以上なのでプログラムを終了させます。

L - Move It 2

Time Limit: 2.5 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 個の箱が並べられており、左から i 番目の箱には番号 i がつけられています。また、 1 から N の番号がついた N 個の荷物があり、荷物 i (1 \le i \le N) の重さは W_i で箱 A_i の中に入っています。

あなたの目標は、各箱にちょうど 1 つの荷物が入っている状態にすることです。そのために、以下の操作を繰り返し行うことができます。

荷物を一つ選び、隣接する箱へ移動させる。移動させる荷物の重さが w のとき、w のコストがかかる。

目標を達成するために必要な操作回数の最小値と、操作回数を最小としたうえでかかるコストの総和の最小値を求めてください。

制約

1\leq N \leq 10^4
1 \leq A_i \leq N (1\leq i\leq N)
1 \leq W_i \leq 10^9 (1\leq i\leq N)
入力はすべて整数

部分点

追加の制約 N \le 500 を満たすデータセットに正解した場合は 1 点が与えられる。

入力

入力は以下の形式で標準入力から与えられます。

N
A_1 A_2 \dots A_N
W_1 W_2 \dots W_N

出力

目標を達成するのに必要な操作回数の最小値と、操作回数を最小にしたうえでかかるコストの総和の最小値を空白区切りで出力してください。

入力例1

3
2 2 2
1 2 3

出力例1

2 3

以下の 2 回の操作で、コストの総和 3 で目標を達成することができます。

荷物 1 を箱 2 から箱 1 に移動させる。コストは 1 かかる。
荷物 2 を箱 2 から箱 3 に移動させる。コストは 2 かかる。

1 回以下の操作で目標は達成できないので、最小の操作回数は 2 です。また、コストの総和を 2 以下にすることはできないので、最小のコストは 3 となります。

入力例2

5
1 2 3 4 5
10 10 10 10 10

出力例2

0 0

初めから目標を達成している場合もあります。

入力例3

5
2 2 3 3 5
33 40 2 12 16

出力例3

2 35

M - NUPaCking

Time Limit: 8 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 頂点 M 辺の単純無向グラフ G が与えられます。ここで、 \mathrm{NUPC} を以下の図で示すグラフとします。

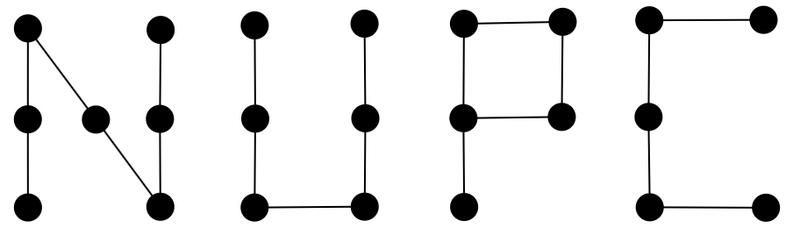
黒い点はグラフの頂点を、それを結んでいる線分はグラフの辺を表します。

G に \mathrm{NUPC} を点素に埋め込むことのできる数の最大値を求めてください。

すなわち、以下を満たす最大の整数 k を求めてください。

G は「 \mathrm{NUPC} が k 個からなるグラフ」を部分グラフとして含む。

制約

1 \le N, M \le 10^5
1 \leq u_i, v_i \leq N
G の各連結成分の頂点数は 10 以下
与えられるグラフは単純である。すなわち、自己ループや多重辺は存在しない。
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

N M
u_1 v_1
u_2 v_2
\vdots
u_M v_M

出力

標準出力へ答えを一行で出力してください。

入力例 1

出力例 1

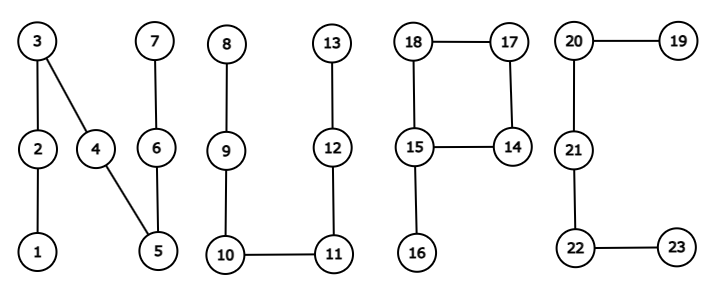
グラフは図のようになっています。このグラフは \mathrm{NUPC} をちょうど 1 個含みます。

入力例 2

出力例 2

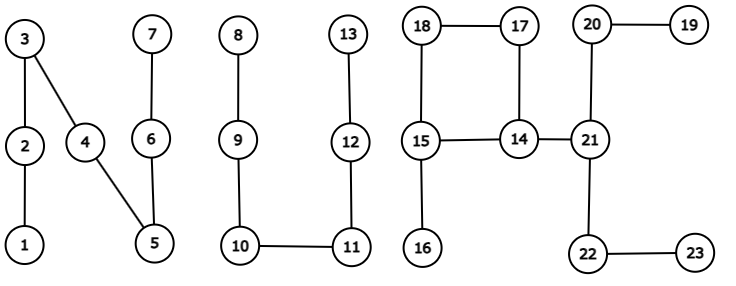
グラフは図のようになっています。 1 つの連結成分に 2 つの文字を埋め込むこともできます。

入力例 3

出力例 3

N - しゃくとり on Namori

Time Limit: 3 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 頂点 N 辺の頂点重み付き単純無向連結グラフ G と正整数 K が与えられます。 i 番目の辺は頂点 u_i と頂点 v_i を結んでいます。また、各頂点 i は正整数の重み A_i を持ちます。

以下を満たす G 上の単純パスの最大の辺数を求めて下さい。

パス上に現れる（端点を含む）頂点の重みの総積が K 以下

単純パスとは？

単純パスとは、 G の頂点の列 P = (p_1, p_2, \dots, p_\ell) であって、「任意の 1 \leq i \leq \ell-1 について、 p_i と p_{i+1} は辺で結ばれている」かつ「同じ頂点は二度現れない」ものです。P の辺数は、 \ell-1 として定義されます。

制約

3 \le N \le 2\times 10^5
1 \le K \le 10^9
1 \le A_i \le K
1 \le u_i < v_i \le N
与えられるグラフは単純無向連結
入力はすべて整数

部分点

追加の制約 N \le 5000 を満たすデータセットに正解した場合は 1 点が与えられます。

入力

入力は以下の形式で標準入力から与えられます。

N K
A_1 A_2 \dots A_N
u_1 v_1
u_2 v_2
\vdots
u_N v_N

出力

標準出力へ答えを一行で出力してください。

入力例 1

6 14
3 2 1 3 2 3
1 2
2 3
3 4
1 4
2 5
3 6

出力例 1

辺数 3 の単純パス (5, 2, 3, 6) の頂点重みの総積は 2 \times 2 \times 1 \times 3 = 12 \leq K = 14 です。一方で、辺数 4 以上の単純パスとその頂点重みの総積は、以下のとおりすべて K より大きいです。

(1, 4, 3, 2, 5) とその逆 : 36
(2, 1, 4, 3, 6) とその逆 : 54
(3, 4, 1, 2, 5) とその逆 : 36
(4, 1, 2, 3, 6) とその逆 : 54
(5, 2, 1, 4, 3, 6) とその逆 : 108

入力例 2

6 108
3 2 1 3 2 3
1 2
2 3
3 4
1 4
2 5
3 6

出力例 2

単純パス (5, 2, 1, 4, 3, 6) の頂点重みの総積は 108 = K であり、これより辺数の大きい単純パスはありません。

入力例 3

6 128
78 85 80 67 20 24
1 2
2 3
3 4
1 4
2 5
3 6

出力例 3

この入力例において、 2 頂点以上からなる単純パスの頂点の重みの総積は K より大きくなります。したがって、 1 頂点のみからなるパス、たとえば (1) が辺数 0 で最大となります。

O - LRUD Maze

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

縦 N 行、横 M 列からなるグリッドが与えられます。上から i 行目、左から j 列目のマスを (i,j) と表記します。グリッドの各マスには L , R , U , D のいずれかの文字が書かれており、今 (i,j) には S_{i,j} が書かれています。

このグリッド上では、今いるマスを (i,j) 、そこに書かれた文字を c として、以下の移動が可能です。

c = L かつ j\neq 1 のとき、マス (i,j-1) に移動する。
c = R かつ j\neq M のとき、マス (i,j+1) に移動する。
c = U かつ i\neq 1 のとき、マス (i-1,j) に移動する。
c = D かつ i\neq N のとき、マス (i+1,j) に移動する。

さて、あなたはこれから以下の操作をちょうど 1 回行います。

整数 1 \le i \le N と 1 \le j \le M を選び、 (i,j) に書かれた文字を L , R , U , D のうち S_{i,j} とは異なる文字に書き換える。

この操作は全部で 3NM 種類あります。それらのうち、「操作後のグリッド上で (1,1) から (N,M) へ到達可能なもの」の数を求めてください。

制約

2 \le N,M \le 1000
N,M は整数
S_{i,j} は L , R , U , D のいずれか

入力

入力は以下の形式で標準入力から与えられます。

N M
S_{1,1} S_{1,2} \dots S_{1,M}
S_{2,1} S_{2,2} \dots S_{2,M}
\vdots
S_{N,1} S_{N,2} \dots S_{N,M}

出力

標準出力へ答えを一行で出力してください。

入力例 1

3 3
RDD
RLD
URU

出力例 1

以下の 3 種類が条件を満たします。

(1,2) を R に変える
(2,2) を R に変える
(2,2) を D に変える

入力例 2

3 3
UUU
RRR
DDD

出力例 2

答えが 0 になる場合もあります。

入力例 3

3 4
RDUU
LRDD
ULRU

出力例 3

P - 偶数けんけん

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題

辺が 1 つもない頂点数 N の無向グラフ G があります。 Q 個のクエリが与えられるので順に処理してください。

クエリは以下の 2 種類のどちらかです。

1 u v : 頂点 u と頂点 v の間に辺を張る。
2 u v : 頂点 u から頂点 v への偶数長のウォークが存在するかを判定し、出力する。

ウォークとは？

グラフ G の頂点 s, t に対して、頂点の列 (v_1,v_2,\ldots,v_k) であって v_1 = s, v_k = t かつ任意の 1\le i\le k-1 について v_i, v_{i+1} が辺で結ばれているものを頂点 s から t へのウォークと呼びます。またこのとき、ウォークの長さは k-1 です。 同じ頂点を複数回通ってよいことに注意してください。

制約

2\le N \le 2\times 10^5
1\le Q \le 2\times 10^5
任意のクエリにおいて、 1\le u \lt v \le N
1 種類目のクエリにおいて、同じ (u, v) は 2 回以上現れない
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

N Q
\mathrm{query}_1
\vdots
\mathrm{query}_Q

各クエリは次の 2 種類の形式のどちらかです。

1 u v

2 u v

出力

2 種類目のクエリについて、偶数長のウォークが存在するときは Yes を、存在しないときは No をそれぞれ 1 行ずつ出力してください。

入力例 1

出力例 1

No
No
Yes
No
Yes

1 種類目のクエリによってグラフは図1〜図4のように変化します。始め、グラフは図1の状態です。

1 番目のクエリ：頂点 1 と頂点 4 の間には長さが偶数のウォークが存在しないので No を出力します。
2 番目のクエリ：頂点 1 と頂点 2 の間に辺が追加され、グラフは図2の状態になります。
3 番目のクエリ：頂点 1 と頂点 4 の間には長さが偶数のウォークが存在しないので No を出力します。
4 番目のクエリ：頂点 2 と頂点 4 の間に辺が追加され、グラフは図3の状態になります。
5 番目のクエリ：頂点 1 と頂点 4 の間には長さ 2 のウォークが存在するので Yes を出力します。
6 番目のクエリ：頂点 2 と頂点 4 の間には奇数長のウォークしか存在しないため、No を出力します。
7 番目のクエリ：頂点 1 と頂点 4 の間に辺が追加され、グラフは図4の状態になります。
8 番目のクエリ：頂点 2 と頂点 4 の間には長さ 2 のウォークが存在するので Yes を出力します。

入力例 2

出力例 2

No
Yes
No
Yes
No
No
Yes
No
Yes
Yes
No
Yes
Yes

Q - Stablest Permutation

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

(1,2,\dots,N) の順列 P=(P_1,P_2,\dots,P_N) の不安定さを以下で定めます。

$$ \max_{1 \leq i < j \leq N} \left|(P_iとP_jを入れ替えた順列の転倒数)-(Pの転倒数)\right| $$

入力で N が与えられます。 (1,2,\dots,N) の順列のうち、不安定さが最小のものを一つ構築してください。

転倒数とは?

数列 (A_1,A_2,\dots,A_N) の転倒数とは、 1 \leq i < j \leq N かつ A_i > A_j を満たす整数組 (i,j) の個数を指します。

制約

2\leq N\leq 2\times10^5
入力はすべて整数

入力

入力は以下の形式で標準入力から与えられます。

出力

(1,2,\dots,N) の順列のうち不安定さが最小のものを一つ、空白区切りで出力してください。解が複数存在する場合、どれを出力しても正解とみなされます。

入力例 1

出力例 1

6 2 1 5 7 3 4

不安定さは 3 で、これより小さくすることはできません。