実行時間制限: 2 sec / メモリ制限: 1024 MiB
問題文
高橋君はデータの加工が行いたいです。
整数 a, b, cと、文字列 s が与えられます。 a + b + c の計算結果と、文字列 s を並べて表示しなさい。
制約
- 1\leq a, b, c \leq 1,000
- 1\leq |s| \leq 100
入力
入力は以下の形式で与えられる。
a b c s
出力
a+b+c と s を空白区切りで 1 行に出力せよ。
入力例 1
1 2 3 test
出力例 1
6 test
- 1+2+3 は 6 なので、上記のように出力します。
入力例 2
72 128 256 myonmyon
出力例 2
456 myonmyon
- 72+128+256 は 456 なので、上記のように出力します。
注意!
CやC++を使うときは、main 関数の型を int で指定し、ちゃんとreturn 0;してください。
Javaを使うときは、クラス名をMainにしてください。mainではコンパイルエラーになります。
補足
以下に各言語ごとの解答例を記載しています。
C での解答例
#include<stdio.h>
int main()
{
int a,b,c;
char s[101];
// 整数の入力
scanf("%d", &a);
// スペース区切りの整数の入力
scanf("%d %d",&b,&c);
// 文字列の入力
scanf("%s",s);
// 出力
printf("%d %s\n",a+b+c,s);
return 0;
}
C++ での解答例
#include<iostream>
using namespace std;
int main()
{
// 整数の入力
int a;
cin >> a;
// スペース区切りの整数の入力
int b,c;
cin >> b >> c;
// 文字列の入力
string s;
cin >> s;
// 出力
cout << (a+b+c) << " " << s << endl;
return 0;
}
Java での解答例
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
// 整数の入力
int a = sc.nextInt();
// スペース区切りの整数の入力
int b = sc.nextInt();
int c = sc.nextInt();
// 文字列の入力
String s = sc.next();
// 出力
System.out.println((a+b+c) + " " + s);
}
}
C# での解答例
using System;
class Program
{
static void Main(string[] args)
{
// 整数の入力
int a = int.Parse(Console.ReadLine());
// スペース区切りの整数の入力
string[] input = Console.ReadLine().Split(' ');
int b = int.Parse(input[0]);
int c = int.Parse(input[1]);
// 文字列の入力
string s = Console.ReadLine();
//出力
Console.WriteLine((a+b+c) + " " + s);
}
}
PHP での解答例
<?php # 整数の入力 fscanf(STDIN, "%d", $a); # スペース区切りの整数の入力 fscanf(STDIN, "%d %d", $b, $c); # 文字列の入力 fscanf(STDIN, "%s", $s); # 出力 echo ($a+$b+$c)." ".$s."\n"; ?>
D での解答例
import std.stdio;
import std.string;
import std.conv;
void main()
{
// 整数の入力
int a = to!int(chomp(readln()));
// スペース区切りの整数の入力
string[] input = split(readln());
int b = to!int(input[0]);
int c = to!int(input[1]);
// 文字列の入力
string s = chomp(readln());
// 出力
writefln("%d %s", a+b+c, s);
}
Go での解答例
package main
import (
"fmt"
)
func main() {
var a, b, c int
var s string
fmt.Scanf("%d", &a)
fmt.Scanf("%d %d", &b, &c)
fmt.Scanf("%s", &s)
fmt.Printf("%d %s\n", a+b+c, s)
}
Python2 での解答例
# -*- coding: utf-8 -*- # 整数の入力 a = int(raw_input()) # スペース区切りの整数の入力 b, c = map(int, raw_input().split()) # 文字列の入力 s = raw_input() # 出力 print str(a+b+c) + " " + s
Python3 での解答例
# -*- coding: utf-8 -*-
# 整数の入力
a = int(input())
# スペース区切りの整数の入力
b, c = map(int, input().split())
# 文字列の入力
s = input()
# 出力
print("{} {}".format(a+b+c, s))
Perl での解答例
# 整数の入力 my $a = <STDIN>; # スペース区切りの整数の入力 my $input = <STDIN>; chomp $input; my ($b, $c) = split / /, $input; $ret = $a + $b + $c; # 文字列の入力 my $s = <STDIN>; chomp $s; # 出力 print "$ret $s\n";
Ruby での解答例
# 整数の入力
a = gets.to_i
# スペース区切りの整数の入力
b,c=gets.chomp.split(" ").map(&:to_i);
# 文字列の入力
s = gets.chomp
# 出力
print("#{a+b+c} #{s}\n")
Haskell での解答例
{- お客様の中でHaskellを書ける方はいらっしゃいますか?
と、Haskellの例がなくて困っていたところを @tanakh さんに助けて頂きました。本当にありがとうございました。-}
import Control.Applicative
main :: IO ()
main = do
-- 整数の入力
a <- readLn
-- スペース区切り整数の入力
[b, c] <- map read . words <$> getLine
-- 文字列の入力
s <- getLine
-- 出力
putStrLn $ show (a + b + c) ++ " " ++ s
Pascal での解答例
var
a, b, c : integer;
s : ShortString;
begin
{ 整数の入力 }
readln(a);
{ スペース区切りの整数の入力 }
read(b);
readln(c);
{ 文字列の入力 }
readln(s);
{ 出力 }
writeln(a+b+c, ' ', s);
end.
JavaScript(Node.js) での解答例
// inputに入力データ全体が入る
function Main(input) {
// 1行目がinput[0], 2行目がinput[1], …に入る
input = input.split("\n");
tmp = input[1].split(" ");
//文字列から10進数に変換するときはparseIntを使います
var a = parseInt(input[0], 10);
var b = parseInt(tmp[0], 10);
var c = parseInt(tmp[1], 10);
var s = input[2];
//出力
console.log('%d %s',a+b+c,s);
}
//*この行以降は編集しないでください(標準入出力から一度に読み込み、Mainを呼び出します)
Main(require("fs").readFileSync("/dev/stdin", "utf8"));
Scala での解答例
// defplus @defplus さん提供
import scala.io.StdIn.*
object Main extends App {
var a = readInt
var num = readLine
var s = readLine
var sum = a + num.split(" ")(0).toInt + num.split(" ")(1).toInt
println(sum + " " + s);
}
Problem
Your task is to process some data.
You are given 3 integers a , b , c and a string s.
Output result of a + b + c and string s with a half-width break.
Constraints
- 1\leq a, b, c \leq 1,000
- 1\leq |s| \leq 100
Input
Input will be given in the following format from Standard Input:
a b c s
Output
Output the result of a+b+c and string s with a half-width break in one line.
Input Example #1
1 2 3 test
Output Example #1
6 test
- 1+2+3 equals to 6.
Input Example #2
72 128 256 myonmyon
Output Example #2
456 myonmyon
- 72+128+256 equals to 456.
Notice
If you are C or C++ programmer, please designate the types of main function as int and not to forget return 0; .
If you are Java programmer, please designate your class name as Main, not main.
References
We prepared some sample answers bellow (Not all programming languages).
Please use these examples as reference.
Example of C
#include<stdio.h>
int main()
{
int a,b,c;
char s[101];
// get a integer
scanf("%d", &a);
// get two integers separated half-width break
scanf("%d %d",&b,&c);
// get a string
scanf("%s",s);
// output
printf("%d %s\n",a+b+c,s);
return 0;
}
Example of C++
#include<iostream>
using namespace std;
int main()
{
// get a integer
int a;
cin >> a;
// get two integers separated with half-width break
int b,c;
cin >> b >> c;
// get a string
string s;
cin >> s;
// output
cout << (a+b+c) << " " << s << endl;
return 0;
}
Example of Java
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
// get a integer
int a = sc.nextInt();
// get two integers separated with half-width break
int b = sc.nextInt();
int c = sc.nextInt();
// get a string
String s = sc.next();
// output
System.out.println((a+b+c) + " " + s);
}
}
Example of C#
using System;
class Program
{
static void Main(string[] args)
{
// get a integer
int a = int.Parse(Console.ReadLine());
// get two integers separated with half-width break
string[] input = Console.ReadLine().Split(' ');
int b = int.Parse(input[0]);
int c = int.Parse(input[1]);
// get a string
string s = Console.ReadLine();
//output
Console.WriteLine((a+b+c) + " " + s);
}
}
Example of PHP
<?php # get a integer fscanf(STDIN, "%d", $a); # get two integers separated with half-width break fscanf(STDIN, "%d %d", $b, $c); # get a string fscanf(STDIN, "%s", $s); # output echo ($a+$b+$c)." ".$s."\n"; ?>
Example of D
import std.stdio;
import std.string;
import std.conv;
void main()
{
// get a integer
int a = to!int(chomp(readln()));
// get two integers separated with half-width break
string[] input = split(readln());
int b = to!int(input[0]);
int c = to!int(input[1]);
// get a string
string s = chomp(readln());
// output
writefln("%d %s", a+b+c, s);
}
Example of Go
package main
import (
"fmt"
)
func main() {
var a, b, c int
var s string
fmt.Scanf("%d", &a)
fmt.Scanf("%d %d", &b, &c)
fmt.Scanf("%s", &s)
fmt.Printf("%d %s\n", a+b+c, s)
}
Example of Python
# -*- coding: utf-8 -*- # get a integer a = int(raw_input()) # get two integers separated with half-width break b, c = map(int, raw_input().split()) # get a string s = raw_input() # output print str(a+b+c) + " " + s
Example of Perl
# get a integer my $a = <STDIN>; # get two integers separated with half-width break my $input = <STDIN>; chomp $input; my ($b, $c) = split / /, $input; $ret = $a + $b + $c; # get a string my $s = <STDIN>; chomp $s; # output print "$ret $s\n";
Example of Ruby
# get a integer
a = gets.to_i
# get two integers separated with half-width break
b,c=gets.chomp.split(" ").map(&:to_i);
# get a string
s = gets.chomp
# output
print("#{a+b+c} #{s}\n")
Example of Haskell
{- supportedby @tanakh -}
import Control.Applicative
main :: IO ()
main = do
-- get a integer
a <- readLn
-- get two integers separated with half-width break
[b, c] <- map read . words <$> getLine
-- get a string
s <- getLine
-- output
putStrLn $ show (a + b + c) ++ " " ++ s
Example of Pascal
var
a, b, c : integer;
s : ShortString;
begin
{ get a integer }
readln(a);
{ get two integers separated with half-width break }
read(b);
readln(c);
{ get a string }
readln(s);
{ output }
writeln(a+b+c, ' ', s);
end.
Example of JavaScript(Node.js)
// parameter "input" gets all data
function Main(input) {
// the first line is assigned to input[0], the second line is assigned to input[1] similarly.
input = input.split("\n");
tmp = input[1].split(" ");
// convert string from integer using "parseInt"
var a = parseInt(input[0], 10);
var b = parseInt(tmp[0], 10);
var c = parseInt(tmp[1], 10);
var s = input[2];
//output
console.log('%d %s',a+b+c,s);
}
// Don't edit this line!
Main(require("fs").readFileSync("/dev/stdin", "utf8"));
Example of Scala
// supported by @defplus
import scala.io.StdIn.*
object Main extends App {
var a = readInt
var num = readLine
var s = readLine
var sum = a + num.split(" ")(0).toInt + num.split(" ")(1).toInt
println(sum + " " + s);
}
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 100 点
問題文
シカのAtCoDeerくんは二つの正整数 a,b を見つけました。 a と b の積が偶数か奇数か判定してください。
制約
- 1 ≤ a,b ≤ 10000
- a,b は整数
入力
入力は以下の形式で標準入力から与えられる。
a b
出力
積が奇数なら Odd と、 偶数なら Even と出力せよ。
入力例 1
3 4
出力例 1
Even
3 × 4 = 12 は偶数なので Even を出力してください。
入力例 2
1 21
出力例 2
Odd
1 × 21 = 21 は奇数なので Odd を出力してください。
Score : 100 points
Problem Statement
AtCoDeer the deer found two positive integers, a and b. Determine whether the product of a and b is even or odd.
Constraints
- 1 ≤ a,b ≤ 10000
- a and b are integers.
Input
Input is given from Standard Input in the following format:
a b
Output
If the product is odd, print Odd; if it is even, print Even.
Sample Input 1
3 4
Sample Output 1
Even
As 3 × 4 = 12 is even, print Even.
Sample Input 2
1 21
Sample Output 2
Odd
As 1 × 21 = 21 is odd, print Odd.
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 100 点
問題文
すぬけ君は 1,2,3 の番号がついた 3 つのマスからなるマス目を持っています。
各マスには 0 か 1 が書かれており、マス i には s_i が書かれています。
すぬけ君は 1 が書かれたマスにビー玉を置きます。
ビー玉が置かれるマスがいくつあるか求めてください。
制約
- s_1, s_2, s_3 は
1あるいは0
入力
入力は以下の形式で標準入力から与えられる。
s_{1}s_{2}s_{3}
出力
答えを出力せよ。
入力例 1
101
出力例 1
2
- マス 1,3 にビー玉が置かれます
入力例 2
000
出力例 2
0
- ビー玉はどのマスにも置かれません
Score : 100 points
Problem Statement
Snuke has a grid consisting of three squares numbered 1, 2 and 3.
In each square, either 0 or 1 is written. The number written in Square i is s_i.
Snuke will place a marble on each square that says 1.
Find the number of squares on which Snuke will place a marble.
Constraints
- Each of s_1, s_2 and s_3 is either
1or0.
Input
Input is given from Standard Input in the following format:
s_{1}s_{2}s_{3}
Output
Print the answer.
Sample Input 1
101
Sample Output 1
2
- A marble will be placed on Square 1 and 3.
Sample Input 2
000
Sample Output 2
0
- No marble will be placed on any square.
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 200 点
問題文
黒板に N 個の正の整数 A_1, ..., A_N が書かれています.
すぬけ君は,黒板に書かれている整数がすべて偶数であるとき,次の操作を行うことができます.
- 黒板に書かれている整数すべてを,2 で割ったものに置き換える.
すぬけ君は最大で何回操作を行うことができるかを求めてください.
制約
- 1 \leq N \leq 200
- 1 \leq A_i \leq 10^9
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 ... A_N
出力
すぬけ君は最大で何回操作を行うことができるかを出力せよ.
入力例 1
3 8 12 40
出力例 1
2
最初,黒板には [8, 12, 40] が書かれています. このとき,書かれている整数はすべて偶数なので,操作を行うことができます.
1 回操作を行った後,黒板には [4, 6, 20] が書かれています. 再び,書かれている整数はすべて偶数なので,操作を行うことができます.
2 回操作を行った後,黒板には [2, 3, 10] が書かれています. この時,奇数 3 が書かれているため,これ以上操作を行うことはできません.
よって,すぬけ君は最大で 2 回操作を行うことができます.
入力例 2
4 5 6 8 10
出力例 2
0
最初から奇数 5 が書かれているため,すぬけ君は一回も操作を行うことができません.
入力例 3
6 382253568 723152896 37802240 379425024 404894720 471526144
出力例 3
8
Score : 200 points
Problem Statement
There are N positive integers written on a blackboard: A_1, ..., A_N.
Snuke can perform the following operation when all integers on the blackboard are even:
- Replace each integer X on the blackboard by X divided by 2.
Find the maximum possible number of operations that Snuke can perform.
Constraints
- 1 \leq N \leq 200
- 1 \leq A_i \leq 10^9
Input
Input is given from Standard Input in the following format:
N A_1 A_2 ... A_N
Output
Print the maximum possible number of operations that Snuke can perform.
Sample Input 1
3 8 12 40
Sample Output 1
2
Initially, [8, 12, 40] are written on the blackboard. Since all those integers are even, Snuke can perform the operation.
After the operation is performed once, [4, 6, 20] are written on the blackboard. Since all those integers are again even, he can perform the operation.
After the operation is performed twice, [2, 3, 10] are written on the blackboard. Now, there is an odd number 3 on the blackboard, so he cannot perform the operation any more.
Thus, Snuke can perform the operation at most twice.
Sample Input 2
4 5 6 8 10
Sample Output 2
0
Since there is an odd number 5 on the blackboard already in the beginning, Snuke cannot perform the operation at all.
Sample Input 3
6 382253568 723152896 37802240 379425024 404894720 471526144
Sample Output 3
8
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 200 点
問題文
あなたは、500 円玉を A 枚、100 円玉を B 枚、50 円玉を C 枚持っています。 これらの硬貨の中から何枚かを選び、合計金額をちょうど X 円にする方法は何通りありますか。
同じ種類の硬貨どうしは区別できません。2 通りの硬貨の選び方は、ある種類の硬貨についてその硬貨を選ぶ枚数が異なるとき区別されます。
制約
- 0 \leq A, B, C \leq 50
- A + B + C \geq 1
- 50 \leq X \leq 20,000
- A, B, C は整数である
- X は 50 の倍数である
入力
入力は以下の形式で標準入力から与えられる。
A B C X
出力
硬貨を選ぶ方法の個数を出力せよ。
入力例 1
2 2 2 100
出力例 1
2
条件を満たす選び方は以下の 2 通りです。
- 500 円玉を 0 枚、100 円玉を 1 枚、50 円玉を 0 枚選ぶ。
- 500 円玉を 0 枚、100 円玉を 0 枚、50 円玉を 2 枚選ぶ。
入力例 2
5 1 0 150
出力例 2
0
合計金額をちょうど X 円にする必要があることに注意してください。
入力例 3
30 40 50 6000
出力例 3
213
Score : 200 points
Problem Statement
You have A 500-yen coins, B 100-yen coins and C 50-yen coins (yen is the currency of Japan). In how many ways can we select some of these coins so that they are X yen in total?
Coins of the same kind cannot be distinguished. Two ways to select coins are distinguished when, for some kind of coin, the numbers of that coin are different.
Constraints
- 0 \leq A, B, C \leq 50
- A + B + C \geq 1
- 50 \leq X \leq 20 000
- A, B and C are integers.
- X is a multiple of 50.
Input
Input is given from Standard Input in the following format:
A B C X
Output
Print the number of ways to select coins.
Sample Input 1
2 2 2 100
Sample Output 1
2
There are two ways to satisfy the condition:
- Select zero 500-yen coins, one 100-yen coin and zero 50-yen coins.
- Select zero 500-yen coins, zero 100-yen coins and two 50-yen coins.
Sample Input 2
5 1 0 150
Sample Output 2
0
Note that the total must be exactly X yen.
Sample Input 3
30 40 50 6000
Sample Output 3
213
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 200 点
問題文
1 以上 N 以下の整数のうち、10 進法での各桁の和が A 以上 B 以下であるものの総和を求めてください。
制約
- 1 \leq N \leq 10^4
- 1 \leq A \leq B \leq 36
- 入力はすべて整数である
入力
入力は以下の形式で標準入力から与えられる。
N A B
出力
1 以上 N 以下の整数のうち、10 進法での各桁の和が A 以上 B 以下であるものの総和を出力せよ。
入力例 1
20 2 5
出力例 1
84
20 以下の整数のうち、各桁の和が 2 以上 5 以下なのは 2,3,4,5,11,12,13,14,20 です。これらの合計である 84 を出力します。
入力例 2
10 1 2
出力例 2
13
入力例 3
100 4 16
出力例 3
4554
Score : 200 points
Problem Statement
Find the sum of the integers between 1 and N (inclusive), whose sum of digits written in base 10 is between A and B (inclusive).
Constraints
- 1 \leq N \leq 10^4
- 1 \leq A \leq B \leq 36
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N A B
Output
Print the sum of the integers between 1 and N (inclusive), whose sum of digits written in base 10 is between A and B (inclusive).
Sample Input 1
20 2 5
Sample Output 1
84
Among the integers not greater than 20, the ones whose sums of digits are between 2 and 5, are: 2,3,4,5,11,12,13,14 and 20. We should print the sum of these, 84.
Sample Input 2
10 1 2
Sample Output 2
13
Sample Input 3
100 4 16
Sample Output 3
4554
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点:200 点
問題文
N 枚のカードがあります. i 枚目のカードには, a_i という数が書かれています.
Alice と Bob は, これらのカードを使ってゲームを行います. ゲームでは, Alice と Bob が交互に 1 枚ずつカードを取っていきます. Alice が先にカードを取ります.
2 人がすべてのカードを取ったときゲームは終了し, 取ったカードの数の合計がその人の得点になります. 2 人とも自分の得点を最大化するように最適な戦略を取った時, Alice は Bob より何点多く取るか求めてください.
制約
- N は 1 以上 100 以下の整数
- a_i \ (1 \leq i \leq N) は 1 以上 100 以下の整数
入力
入力は以下の形式で標準入力から与えられる.
N a_1 a_2 a_3 ... a_N
出力
両者が最適な戦略を取った時, Alice は Bob より何点多く取るかを出力してください.
入力例 1
2 3 1
出力例 1
2
最初, Alice は 3 が書かれたカードを取ります. 次に, Bob は 1 が書かれたカードを取ります. 得点差は 3 - 1 = 2 となります.
入力例 2
3 2 7 4
出力例 2
5
最初, Alice は 7 が書かれたカードを取ります. 次に, Bob は 4 が書かれたカードを取ります. 最後に, Alice は 2 が書かれたカードを取ります. 得点差は, 7 - 4 + 2 = 5 点となります.
入力例 3
4 20 18 2 18
出力例 3
18
Score: 200 points
Problem Statement
We have N cards. A number a_i is written on the i-th card.
Alice and Bob will play a game using these cards. In this game, Alice and Bob alternately take one card. Alice goes first.
The game ends when all the cards are taken by the two players, and the score of each player is the sum of the numbers written on the cards he/she has taken. When both players take the optimal strategy to maximize their scores, find Alice's score minus Bob's score.
Constraints
- N is an integer between 1 and 100 (inclusive).
- a_i \ (1 \leq i \leq N) is an integer between 1 and 100 (inclusive).
Input
Input is given from Standard Input in the following format:
N a_1 a_2 a_3 ... a_N
Output
Print Alice's score minus Bob's score when both players take the optimal strategy to maximize their scores.
Sample Input 1
2 3 1
Sample Output 1
2
First, Alice will take the card with 3. Then, Bob will take the card with 1. The difference of their scores will be 3 - 1 = 2.
Sample Input 2
3 2 7 4
Sample Output 2
5
First, Alice will take the card with 7. Then, Bob will take the card with 4. Lastly, Alice will take the card with 2. The difference of their scores will be 7 - 4 + 2 = 5. The difference of their scores will be 3 - 1 = 2.
Sample Input 3
4 20 18 2 18
Sample Output 3
18
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 200 点
問題文
X 段重ねの鏡餅 (X ≥ 1) とは、X 枚の円形の餅を縦に積み重ねたものであって、どの餅もその真下の餅より直径が小さい(一番下の餅を除く)もののことです。例えば、直径 10、8、6 センチメートルの餅をこの順に下から積み重ねると 3 段重ねの鏡餅になり、餅を一枚だけ置くと 1 段重ねの鏡餅になります。
ダックスフンドのルンルンは N 枚の円形の餅を持っていて、そのうち i 枚目の餅の直径は d_i センチメートルです。これらの餅のうち一部または全部を使って鏡餅を作るとき、最大で何段重ねの鏡餅を作ることができるでしょうか。
制約
- 1 ≤ N ≤ 100
- 1 ≤ d_i ≤ 100
- 入力値はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N d_1 : d_N
出力
作ることのできる鏡餅の最大の段数を出力せよ。
入力例 1
4 10 8 8 6
出力例 1
3
直径 10、8、6 センチメートルの餅をこの順に下から積み重ねると 3 段重ねの鏡餅になり、これが最大です。
入力例 2
3 15 15 15
出力例 2
1
すべての餅の直径が同じときは、1 段重ねの鏡餅しか作れません。
入力例 3
7 50 30 50 100 50 80 30
出力例 3
4
Score : 200 points
Problem Statement
An X-layered kagami mochi (X ≥ 1) is a pile of X round mochi (rice cake) stacked vertically where each mochi (except the bottom one) has a smaller diameter than that of the mochi directly below it. For example, if you stack three mochi with diameters of 10, 8 and 6 centimeters from bottom to top in this order, you have a 3-layered kagami mochi; if you put just one mochi, you have a 1-layered kagami mochi.
Lunlun the dachshund has N round mochi, and the diameter of the i-th mochi is d_i centimeters. When we make a kagami mochi using some or all of them, at most how many layers can our kagami mochi have?
Constraints
- 1 ≤ N ≤ 100
- 1 ≤ d_i ≤ 100
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N d_1 : d_N
Output
Print the maximum number of layers in a kagami mochi that can be made.
Sample Input 1
4 10 8 8 6
Sample Output 1
3
If we stack the mochi with diameters of 10, 8 and 6 centimeters from bottom to top in this order, we have a 3-layered kagami mochi, which is the maximum number of layers.
Sample Input 2
3 15 15 15
Sample Output 2
1
When all the mochi have the same diameter, we can only have a 1-layered kagami mochi.
Sample Input 3
7 50 30 50 100 50 80 30
Sample Output 3
4
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 300 点
問題文
日本でよく使われる紙幣は、10000 円札、5000 円札、1000 円札です。以下、「お札」とはこれらのみを指します。
青橋くんが言うには、彼が祖父から受け取ったお年玉袋にはお札が N 枚入っていて、合計で Y 円だったそうですが、嘘かもしれません。このような状況がありうるか判定し、ありうる場合はお年玉袋の中身の候補を一つ見つけてください。なお、彼の祖父は十分裕福であり、お年玉袋は十分大きかったものとします。
制約
- 1 ≤ N ≤ 2000
- 1000 ≤ Y ≤ 2 × 10^7
- N は整数である。
- Y は 1000 の倍数である。
入力
入力は以下の形式で標準入力から与えられる。
N Y
出力
N 枚のお札の合計金額が Y 円となることがありえない場合は、-1 -1 -1 と出力せよ。
N 枚のお札の合計金額が Y 円となることがありうる場合は、そのような N 枚のお札の組み合わせの一例を「10000 円札 x 枚、5000 円札 y 枚、1000 円札 z 枚」として、x、y、z を空白で区切って出力せよ。複数の可能性が考えられるときは、そのうちどれを出力してもよい。
入力例 1
9 45000
出力例 1
4 0 5
お年玉袋に 10000 円札 4 枚と 1000 円札 5 枚が入っていれば、合計枚数が 9 枚、合計金額が 45000 円になります。5000 円札 9 枚という可能性も考えられるため、0 9 0 も正しい出力です。
入力例 2
20 196000
出力例 2
-1 -1 -1
合計枚数が 20 枚の場合、すべてが 10000 円札であれば合計金額は 200000 円になり、そうでなければ 195000 円以下になるため、196000 円という合計金額はありえません。
入力例 3
1000 1234000
出力例 3
14 27 959
この他にも多くの候補があります。
入力例 4
2000 20000000
出力例 4
2000 0 0
Score : 300 points
Problem Statement
The commonly used bills in Japan are 10000-yen, 5000-yen and 1000-yen bills. Below, the word "bill" refers to only these.
According to Aohashi, he received an otoshidama (New Year money gift) envelope from his grandfather that contained N bills for a total of Y yen, but he may be lying. Determine whether such a situation is possible, and if it is, find a possible set of bills contained in the envelope. Assume that his grandfather is rich enough, and the envelope was large enough.
Constraints
- 1 ≤ N ≤ 2000
- 1000 ≤ Y ≤ 2 × 10^7
- N is an integer.
- Y is a multiple of 1000.
Input
Input is given from Standard Input in the following format:
N Y
Output
If the total value of N bills cannot be Y yen, print -1 -1 -1.
If the total value of N bills can be Y yen, let one such set of bills be "x 10000-yen bills, y 5000-yen bills and z 1000-yen bills", and print x, y, z with spaces in between. If there are multiple possibilities, any of them may be printed.
Sample Input 1
9 45000
Sample Output 1
4 0 5
If the envelope contained 4 10000-yen bills and 5 1000-yen bills, he had 9 bills and 45000 yen in total. It is also possible that the envelope contained 9 5000-yen bills, so the output 0 9 0 is also correct.
Sample Input 2
20 196000
Sample Output 2
-1 -1 -1
When the envelope contained 20 bills in total, the total value would be 200000 yen if all the bills were 10000-yen bills, and would be at most 195000 yen otherwise, so it would never be 196000 yen.
Sample Input 3
1000 1234000
Sample Output 3
14 27 959
There are also many other possibilities.
Sample Input 4
2000 20000000
Sample Output 4
2000 0 0
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 300 点
問題文
英小文字からなる文字列 S が与えられます。 Tが空文字列である状態から始め、以下の操作を好きな回数繰り返すことで S = T とすることができるか判定してください。
- T の末尾に
dreamdreamereraseeraserのいずれかを追加する。
制約
- 1≦|S|≦10^5
- S は英小文字からなる。
入力
入力は以下の形式で標準入力から与えられる。
S
出力
S = T とすることができる場合 YES を、そうでない場合 NO を出力せよ。
入力例 1
erasedream
出力例 1
YES
erase dream の順で T の末尾に追加することで S = T とすることができます。
入力例 2
dreameraser
出力例 2
YES
dream eraser の順で T の末尾に追加することで S = T とすることができます。
入力例 3
dreamerer
出力例 3
NO
Score : 300 points
Problem Statement
You are given a string S consisting of lowercase English letters. Another string T is initially empty. Determine whether it is possible to obtain S = T by performing the following operation an arbitrary number of times:
- Append one of the following at the end of T:
dream,dreamer,eraseanderaser.
Constraints
- 1≦|S|≦10^5
- S consists of lowercase English letters.
Input
The input is given from Standard Input in the following format:
S
Output
If it is possible to obtain S = T, print YES. Otherwise, print NO.
Sample Input 1
erasedream
Sample Output 1
YES
Append erase and dream at the end of T in this order, to obtain S = T.
Sample Input 2
dreameraser
Sample Output 2
YES
Append dream and eraser at the end of T in this order, to obtain S = T.
Sample Input 3
dreamerer
Sample Output 3
NO
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 300 点
問題文
シカのAtCoDeerくんは二次元平面上で旅行をしようとしています。 AtCoDeerくんの旅行プランでは、時刻 0 に 点 (0,0) を出発し、 1 以上 N 以下の各 i に対し、時刻 t_i に 点 (x_i,y_i) を訪れる予定です。
AtCoDeerくんが時刻 t に 点 (x,y) にいる時、 時刻 t+1 には 点 (x+1,y), (x-1,y), (x,y+1), (x,y-1) のうちいずれかに存在することができます。 その場にとどまることは出来ないことに注意してください。 AtCoDeerくんの旅行プランが実行可能かどうか判定してください。
制約
- 1 ≤ N ≤ 10^5
- 0 ≤ x_i ≤ 10^5
- 0 ≤ y_i ≤ 10^5
- 1 ≤ t_i ≤ 10^5
- t_i < t_{i+1} (1 ≤ i ≤ N-1)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N t_1 x_1 y_1 t_2 x_2 y_2 : t_N x_N y_N
出力
旅行プランが実行可能ならYesを、不可能ならNoを出力してください。
入力例 1
2 3 1 2 6 1 1
出力例 1
Yes
例えば、(0,0), (0,1), (1,1), (1,2), (1,1), (1,0), (1,1) と移動すればよいです。
入力例 2
1 2 100 100
出力例 2
No
(0,0) にいる状態から 2 秒後に (100,100) にいるのは不可能です。
入力例 3
2 5 1 1 100 1 1
出力例 3
No
Score : 300 points
Problem Statement
AtCoDeer the deer is going on a trip in a two-dimensional plane. In his plan, he will depart from point (0, 0) at time 0, then for each i between 1 and N (inclusive), he will visit point (x_i,y_i) at time t_i.
If AtCoDeer is at point (x, y) at time t, he can be at one of the following points at time t+1: (x+1,y), (x-1,y), (x,y+1) and (x,y-1). Note that he cannot stay at his place. Determine whether he can carry out his plan.
Constraints
- 1 ≤ N ≤ 10^5
- 0 ≤ x_i ≤ 10^5
- 0 ≤ y_i ≤ 10^5
- 1 ≤ t_i ≤ 10^5
- t_i < t_{i+1} (1 ≤ i ≤ N-1)
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N t_1 x_1 y_1 t_2 x_2 y_2 : t_N x_N y_N
Output
If AtCoDeer can carry out his plan, print Yes; if he cannot, print No.
Sample Input 1
2 3 1 2 6 1 1
Sample Output 1
Yes
For example, he can travel as follows: (0,0), (0,1), (1,1), (1,2), (1,1), (1,0), then (1,1).
Sample Input 2
1 2 100 100
Sample Output 2
No
It is impossible to be at (100,100) two seconds after being at (0,0).
Sample Input 3
2 5 1 1 100 1 1
Sample Output 3
No
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
これはインタラクティブ形式の例題です。初心者向け問題ではありませんので注意してください。
初心者の方は、AtCoder Beginners Selectionに挑戦してみてください!
最初の N 個の大文字でラベルの付いた N 個のボールがあります。 どの二つのボールの重さも異なります。
あなたは Q 回クエリを質問することができます。 各クエリでは、二つのボールの重さを比べることができます。(詳しくは入出力セクションを見てください)
ボールを軽い順にソートしてください。
制約
- (N, Q) = (26, 1000), (26, 100), (5, 7) のいずれかである。
部分点
三つのテストセットがある。各セットは 100 点ずつである。
- テストセット 1: N = 26, Q = 1000
- テストセット 2: N = 26, Q = 100
- テストセット 3: N = 5, Q = 7
入出力
最初に、標準入力から N と Q が以下の形式で与えられる:
N Q
次に、あなたは Q 回以下クエリを質問する。 各クエリは、標準出力に以下の形式で出力されなければならない:
? c_1 c_2
ここで c_1 と c_2 は異なる最初の N 個の大文字のどれかでなければならない。
次に、クエリの答えが標準入力から以下の形式で与えられる:
ans
ここで ans は < または > である。
< のときは c_2 のほうが重く、> のときは c_1 のほうが重い。
最後に、答えを以下の形式で出力しなければならない:
! ans
ここで ans は N 文字の文字列であり、最初の N 個の大文字を軽い順に並べたものでなければならない。
ジャッジ
- 出力のあと、標準出力を flush しなければならない。 そうでないときは
TLEの可能性がある。 - 答えを出力した後、プログラムをすぐに終了しなければならない。そうでないときの挙動は定義されていない。
- 出力の答えが間違っている場合の挙動は定義されていない (
WAとは限らない)。
コード例
以下のコードは、C++ で 100 点を獲得するための例です。部分点を取得可能なコードなので、提出するとWAになります。
#include <cstdio>
#include <string>
using namespace std;
int main(void){
int N,Q,i,j;
scanf("%d%d", &N, &Q);
string s;
for(i=0;i<N;i++) s += (char)('A' + i);
for(i=0;i<N;i++) for(j=0;j<N-1;j++){
printf("? %c %c\n", s[j], s[j+1]);
fflush(stdout);
char ans;
scanf(" %c", &ans);
if(ans == '>') swap(s[j], s[j+1]);
}
printf("! %s\n", s.c_str());
fflush(stdout);
return 0;
}
サンプル
このサンプルでは N = 3, Q = 10 で、答えは BAC である。
| Input | Output |
|---|---|
| 3 10 | |
| ? A B | |
| > | |
| ? C B | |
| > | |
| ? A C | |
| < | |
| ! BAC |
Score : 300 points
Problem Statement
This is an interactive task. Please note that these are not beginner questions.
If you are a beginner, try the AtCoder Beginners Selection!
There are N balls labeled with the first N uppercase letters. The balls have pairwise distinct weights.
You are allowed to ask at most Q queries. In each query, you can compare the weights of two balls (see Input/Output section for details).
Sort the balls in the ascending order of their weights.
Constraints
- (N, Q) = (26, 1000), (26, 100), or (5, 7).
Partial Score
There are three testsets. Each testset is worth 100 points.
- In testset 1, N = 26 and Q = 1000.
- In testset 2, N = 26 and Q = 100.
- In testset 3, N = 5 and Q = 7.
Input and Output
First, you are given N and Q from Standard Input in the following format:
N Q
Then, you start asking queries (at most Q times). Each query must be printed to Standard Output in the following format:
? c_1 c_2
Here each of c_1 and c_2 must be one of the first N uppercase letters, and c_1 and c_2 must be distinct.
Then, you are given the answer to the query from Standard Input in the following format:
ans
Here ans is either < or >.
When ans is <, the ball c_2 is heavier than the ball c_1, and otherwise the ball c_1 is heavier than the ball c_2.
Finally, you must print the answer to Standard Output in the following format:
! ans
Here ans must be a string of length N, and it must contain each of the first N uppercase letters once. It must represent the weights of the balls in the ascending order.
Judgement
- After each output, you must flush Standard Output. Otherwise you may get
TLE. - After you print the answer, the program must be terminated immediately. Otherwise, the behavior of the judge is undefined.
- When your output is invalid or incorrect, the behavior of the judge is undefined (it does not necessarily give
WA).
Sample Code
Here is a sample solution for 100 points. The code is obtainable for partial points, so submitting it will result in a WA.
#include <cstdio>
#include <string>
using namespace std;
int main(void){
int N,Q,i,j;
scanf("%d%d", &N, &Q);
string s;
for(i=0;i<N;i++) s += (char)('A' + i);
for(i=0;i<N;i++) for(j=0;j<N-1;j++){
printf("? %c %c\n", s[j], s[j+1]);
fflush(stdout);
char ans;
scanf(" %c", &ans);
if(ans == '>') swap(s[j], s[j+1]);
}
printf("! %s\n", s.c_str());
fflush(stdout);
return 0;
}
Sample
In this sample N = 3, Q = 10, and the answer is BAC.
| Input | Output |
|---|---|
| 3 10 | |
| ? A B | |
| > | |
| ? C B | |
| > | |
| ? A C | |
| < | |
| ! BAC |
実行時間制限: 3 sec / メモリ制限: 1024 MiB
問題文
あなたは、モンスターの調教師です。モンスター「高橋君」を育てて、所持金を出来るだけ増やしましょう!
高橋君はたくさんのスキルを持ち、それらをトレーニングで向上させながら、野良モンスターを討伐して報酬を稼ぐことが出来ます。
高橋君が持つスキルは N = 10 種類で、はじめ全てのスキルのレベルは 0 です。各スキルのレベルは最大 10 まで上げることが出来ます。また、現在のあなたの所持金は 1000 円です。
T = 1000 ターンが与えられます。各ターンには、以下の 3 種類の行動からどれか 1 つを行うことが出来ます。
- アルバイト: 所持金が 1000 円増える。
- トレーニング: N = 10 種類のスキルから 1 つを選び、そのスキルのトレーニングを 1 回行う。
- スキルのレベルを k-1 から k (1≦k≦10) に上げるには、k 回のトレーニングが必要である。各回のトレーニングには 10000×2^k 円の費用がかかる。
- レベル 10 のスキルについてトレーニングを行おうとした場合は失敗し、所持金は減らない。
- 所持金が足りない場合もトレーニングに失敗し、所持金は減らない。
- 討伐: M = 30000 個の野良モンスターの討伐依頼から、どれか 1 つを選んで受注する。
- i 番目の依頼には、10 種類のスキルの要求レベル S_{i,1}, S_{i,2}, ..., S_{i,10} と基本報酬額 C_i が設定されている。
- 要求レベルに達していないスキルがあっても依頼を受注することは出来るが、1 種類のスキルについてレベルが 1 不足するごとに報酬が半減する。(詳しくは下記の計算式を参照)
- すべてのスキルが要求レベル以上である場合、討伐は大成功し、報酬は 10 倍となる。
- また、各依頼には討伐申込開始ターン A_i と討伐申込締切ターン B_i も設定されている。
- A_i ターン目より早く、または B_i ターン目より遅くその依頼を受注することは出来ない。このような依頼を受注しようとした場合、何も起こらずにターンが終了する。(A_i ターン目または B_i ターン目ちょうどの受注は可能)
- 報酬は締切に近ければ近いほど高くなり、締切ターンでの報酬は開始ターンの 10 倍となる。
- より具体的には、実報酬額は以下の計算式で計算される。
- (実報酬額) = floor((基本報酬額 C_i) × (締切報酬レート) × (スキル倍率))
- 締切報酬レートは、受注ターンを X として以下となる。
- (締切報酬レート) = 1 + 9 × (X - A_i) ÷ (B_i - A_i)
- スキル倍率は、すべてのスキルが要求レベル以上であるとき 10、そうでないとき (1/2)^Y となる。
- ここで、Y は要求レベルに達していないスキルすべてについての不足するレベルの総和である。
- より厳密には、当ページ下部の「疑似コード」セクションを参照せよ。
- 各依頼は一度しか受注することが出来ない。一度受注した依頼を再度受注しようとした場合、何も起こらずにターンが終了する。
1000 ターンの間の行動を出力し、最終的な所持金を最大化してください。
制約
- T = 1000
- N = 10
- M = 30000
- 各 i (1≦i≦M) について、1 ≦ A_i < B_i ≦ T, 1 ≦ C_i ≦ 10^{15}
- 各ペア i, j (1≦i≦M, 1≦j≦N) について、0 ≦ S_{i,j} ≦ 10
- 与えられるすべての値は整数
入力
入力は以下の形式で与えられる。
T N M
A_1 B_1 C_1 S_{1,1} S_{1,2} ... S_{1,N}
A_2 B_2 C_2 S_{2,1} S_{2,2} ... S_{2,N}
:
A_M B_M C_M S_{M,1} S_{M,2} ... S_{M,N}
出力
1000 ターンの間の行動を出力せよ。
出力は以下の形式で行うこと。
Command_1
Command_2
:
Command_{1000}
Command_iは i ターン目に行う行動を表し、以下のように指定する。- トレーニングを行う場合、
1 A_iとする。A_i (1≦A_i≦N) は、i ターン目にトレーニングを行うスキルの番号である。 - 討伐依頼の受注を行う場合、
2 B_iとする。B_i (1≦B_i≦M) は、i ターン目に受注する討伐依頼の番号である。 - アルバイトを行う場合、
3とする。
- トレーニングを行う場合、
入力生成
この項は必ずしも目を通す必要はない。
各テストケースにおける M 個の討伐依頼は、それぞれ独立に以下のアルゴリズムで生成されたものである。
- 討伐申込可能期間を、「短期間」「中期間」「長期間」の 3 つから、均等な確率でランダムに選択する。
- 討伐申込可能期間 L_i を決定する。短期間の場合は 2 ~ 10、中期間の場合は 11 ~ 100、長期間の場合は 101 ~ 1000 の間で、均等な確率でランダムで決定される。
- 討伐申込開始ターン A_i を決定する。1 ~ T - L_i + 1 の間で、均等な確率でランダムに決定される。 B_i = A_i + L_i - 1 となる。
- スキルの要求レベルを、高い順に決定していく。
- 1 番目に高い要求レベルは、1~10 の間でランダムに決定される。これを s_1 とする。
- 2 番目に高い要求レベルは、0~s_1 の間でランダムに決定される。これを s_2 とする。
- 3 番目に高い要求レベルは、0~s_2 の間でランダムに決定される。これを s_3 とする。
- これを繰り返し、 s_{10} まで決定する。
- s をランダムに並び替えたものを、その討伐依頼の要求レベル S_i とする。
- 要求レベルの和を Sum とすると、基準報酬額 M_i は M_i = 1.3^{Sum} で決定される。これに 1~2000 のランダムに決定された整数値を掛け、小数点以下を切り捨てた値を基本報酬額 C_i とする。
採点
各テストケースにおける点数は、1000 ターン後のあなたの所持金額そのものである。
テストケースは 30 個与えられる。全てのテストケースの点数の相乗平均が、その提出の得点となる。1 ケースでも出力が不正であった場合、提出の得点は 0 点となる。
ただし、サンプル入力についてのみ、最終的な所持金額を 0.01 倍した値を上記の得点にさらに加算する。この結果が提出の最終得点である。
追記 点数が大きすぎて順位表が見づらいため、点数をさらに 0.0001 倍したものを最終点数とする。
疑似コード
報酬の計算について、以下の疑似コードを利用して良い。これは、t ターン目に i 番目の討伐依頼を受注した際の実報酬額である。
double AddMoney = C[i];
AddMoney *= (1 + 9 * (double)(t - A[i]) / (B[i] - A[i]));
int SkillLack = 0;
for (int j = 0; j < N; j++) SkillLack += max(0, S[i][j] - SkillLevel[j]);
if (SkillLack == 0) AddMoney *= 10;
else {
AddMoney *= pow(0.5, SkillLack);
AddMoney += 1e-9;
}
Money += (long long)AddMoney;
入力例1
採点結果の「example_01」が、こちらのデータとなります。このデータも採点対象(相乗平均の計算に使われる 30 ケースのうちの 1 つ)となります。
実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 頂点 0 辺の無向グラフに Q 個のクエリが飛んできます。処理してください。
0 u v: 辺(u, v)を追加する。1 u v: u, v が連結ならば 1、そうでないなら 0 を出力する。
制約
- 1 \leq N \leq 200,000
- 1 \leq Q \leq 200,000
- 0 \leq u_i, v_i \lt N
入力
N Q t_1 u_1 v_1 t_2 u_2 v_2 : t_Q u_Q v_Q
出力
クエリ 1 ごとに各行に出力してください。
入力例 1
4 7 1 0 1 0 0 1 0 2 3 1 0 1 1 1 2 0 0 2 1 1 3
出力例 1
0 1 0 1
Score : 100 points
Problem Statement
You are given an undirected graph with N vertices and 0 edges. Process Q queries of the following types.
0 u v: Add an edge (u, v).1 u v: Print 1 if u and v are in the same connected component, 0 otherwise.
Constraints
- 1 \leq N \leq 200,000
- 1 \leq Q \leq 200,000
- 0 \leq u_i, v_i \lt N
Input
Input is given from Standard Input in the following format:
N Q t_1 u_1 v_1 t_2 u_2 v_2 : t_Q u_Q v_Q
出力
For each query of the latter type, print the answer.
Sample Input 1
4 7 1 0 1 0 0 1 0 2 3 1 0 1 1 1 2 0 0 2 1 1 3
Sample Output 1
0 1 0 1
出典
Based on Library Checker (Unionfind) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
長さ N の数列 a_0, a_1, ..., a_{N-1} に Q 個のクエリが飛んできます。処理してください。
0 p x: a_p \gets a_p + x1 l r: \sum_{i = l}^{r - 1}{a_i} を出力する。
制約
- 1 \leq N, Q \leq 500,000
- 0 \leq a_i, x \leq 10^9
- 0 \leq p < N
- 0 \leq l_i < r_i \leq N
入力
N Q
a_0 a_1 ... a_{N - 1}
\textrm{Query}_0
\textrm{Query}_1
:
\textrm{Query}_{Q - 1}
出力
クエリ 1 ごとに各行に出力してください。
入力例 1
5 5 1 2 3 4 5 1 0 5 1 2 4 0 3 10 1 0 5 1 0 3
出力例 1
15 7 25 6
Score : 100 points
Problem Statement
You are given an array a_0, a_1, ..., a_{N-1} of length N. Process Q queries of the following types.
0 p x: a_p \gets a_p + x1 l r: Print \sum_{i = l}^{r - 1}{a_i}.
Constraints
- 1 \leq N, Q \leq 500,000
- 0 \leq a_i, x \leq 10^9
- 0 \leq p < N
- 0 \leq l_i < r_i \leq N
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N Q
a_0 a_1 ... a_{N - 1}
\textrm{Query}_0
\textrm{Query}_1
:
\textrm{Query}_{Q - 1}
Output
For each query of the latter type, print the answer.
Sample Input 1
5 5 1 2 3 4 5 1 0 5 1 2 4 0 3 10 1 0 5 1 0 3
Sample Output 1
15 7 25 6
出典
Based on Library Checker (Point Add Range Sum) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
この問題は T ケース与えられます。
N, M, A, B が与えられます。
\sum_{i = 0}^{N - 1} floor((A \times i + B) / M) を求めてください。
制約
- 1 \leq T \leq 100,000
- 1 \leq N, M \leq 10^9
- 0 \leq A, B < M
入力
T
N_0 M_0 A_0 B_0
N_1 M_1 A_1 B_1
:
N_{T - 1} M_{T - 1} A_{T - 1} B_{T - 1}
出力
入力例 1
5 4 10 6 3 6 5 4 3 1 1 0 0 31415 92653 58979 32384 1000000000 1000000000 999999999 999999999
出力例 1
3 13 0 314095480 499999999500000000
Score : 100 points
Problem Statement
In this problem, you should process T testcases.
For each testcase, you are given four integers N, M, A, B.
Calculate \sum_{i = 0}^{N - 1} floor((A \times i + B) / M).
Constraints
- 1 \leq T \leq 100,000
- 1 \leq N, M \leq 10^9
- 0 \leq A, B < M
Input
Input is given from Standard Input in the following format:
T
N_0 M_0 A_0 B_0
N_1 M_1 A_1 B_1
:
N_{T - 1} M_{T - 1} A_{T - 1} B_{T - 1}
Output
Print the answer for each testcase.
Sample Input 1
5 4 10 6 3 6 5 4 3 1 1 0 0 31415 92653 58979 32384 1000000000 1000000000 999999999 999999999
Sample Output 1
3 13 0 314095480 499999999500000000
出典
Based on Library Checker (Sum of Floor of Linear) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 行 M 列のマス目があります. 上から i 行目,左から j 番目のマス目をマス (i,j) と呼ぶことにします.
現在,それぞれのマスは,障害物が置かれているか,空であるかのどちらかの状態です.
これらの状態は,文字列 S_1,S_2,\cdots,S_N によって表され,
マス (i,j) の状態は,S_{i,j}= # なら障害物が置かれていること,S_{i,j}= . なら空であることを意味します.
これらのマスに,1 \times 2 の大きさのタイルを置きたいです. タイルは,縦または横に連続する 2 つの空マスの上に置くことができます. タイルを盤面からはみ出すように置くことや,障害物や他のタイルがすでに置かれているマスにタイルを重ねることは禁止されています. 最大でいくつのタイルを置くことができるか求めてください. また,実際にその最大値を達成する方法を 1 つ示してください.
制約
- 1 \leq N \leq 100
- 1 \leq M \leq 100
- S_i は
#と.のみからなる長さ M の文字列
入力
入力は以下の形式で標準入力から与えられる.
N M S_1 S_2 \vdots S_N
出力
1 行目には,置くことのできるタイルの枚数の最大値を出力せよ.
続く N 行には,実際にその最大値を達成するタイルの置き方を出力せよ.
具体的には,以下のような手順で得られる文字列 t_1,t_2,\cdots,t_N を出力せよ.
- まず,t_i=S_i と初期化する.
- マス (i,j) と (i+1,j) にまたがるタイルを置く場合,t_{i,j}:=
v, t_{i+1,j}:=^と変更する. - マス (i,j) と (i,j+1) にまたがるタイルを置く場合,t_{i,j}:=
>, t_{i,j+1}:=<と変更する.
具体的な例については,入出力例を参考にせよ.
なお,最大値を達成するタイルの置き方が複数存在する場合,どれを出力してもよい.
入力例 1
3 3 #.. ..# ...
出力例 1
3 #>< vv# ^^.
この例の場合,次のような出力も正解となります.
3 #>< v.# ^><
Score : 100 points
Problem Statement
You are given a grid of N rows and M columns. The square at the i-th row and j-th column will be denoted as (i,j).
Some of the squares contain an object. All the remaining squares are empty.
The state of the grid is represented by strings S_1,S_2,\cdots,S_N. The square (i,j) contains an object if S_{i,j}= # and is empty if S_{i,j}= ..
Consider placing 1 \times 2 tiles on the grid. Tiles can be placed vertically or horizontally to cover two adjacent empty squares. Tiles must not stick out of the grid, and no two different tiles may intersect. Tiles cannot occupy the square with an object.
Calculate the maximum number of tiles that can be placed and any configulation that acheives the maximum.
Constraints
- 1 \leq N \leq 100
- 1 \leq M \leq 100
- S_i is a string with length M consists of
#and..
Input
Input is given from Standard Input in the following format:
N M S_1 S_2 \vdots S_N
Output
On the first line, print the maximum number of tiles that can be placed.
On the next N lines, print a configulation that achieves the maximum. Precisely, output the strings t_1,t_2,\cdots,t_N constructed by the following way.
- t_i is initialized to S_i.
- For each (i,j), if there is a tile that occupies (i,j) and (i+1,j), change t_{i,j}:=
v, t_{i+1,j}:=^. - For each (i,j), if there is a tile that occupies (i,j) and (i,j+1), change t_{i,j}:=
>, t_{i,j+1}:=<.
See samples for further information.
You may print any configulation that maximizes the number of tiles.
Sample Input 1
3 3 #.. ..# ...
Sample Output 1
3 #>< vv# ^^.
The following output is also treated as a correct answer.
3 #>< v.# ^><
実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 行 N 列のマス目があります. 上から i 行目,左から j 番目のマスをマス (i,j) と呼ぶことにします. それぞれのマスには非負整数が書かれており,マス (i,j) に書かれている数は A_{i,j} です.
これらのマスのうちいくつかを選び,選んだマスに書かれている数の総和を最大化したいです. ただし,どの行についても,その行の中で選ばれたマスの個数は K 個以下である必要があります. また同様に,どの列についても,その列の中で選ばれたマスの個数は K 個以下である必要があります.
選んだマスに書かれている数の総和の最大値を求めてください. また,その最大値を達成する方法を 1 つ示してください.
制約
- 1 \leq N \leq 50
- 1 \leq K \leq N
- 0 \leq A_{i,j} \leq 10^9
- 入力される数は全て整数である.
入力
入力は以下の形式で標準入力から与えられる.
N K
A_{1,1} A_{1,2} \cdots A_{1,N}
A_{2,1} A_{2,2} \cdots A_{2,N}
\vdots
A_{N,1} A_{N,2} \cdots A_{N,N}
出力
1 行目には,選んだマスに書かれている数の総和の最大値を出力せよ.
続く N 行には,実際にその最大値を達成するマスの選び方を出力せよ.
具体的には,文字列 t_1,t_2,\cdots,t_N を出力せよ.
ただしここで t_i はマスの選び方を表す文字列で,
マス (i,j) を選ぶときは t_{i,j}=X,選ばないときは t_{i,j}=. とせよ.
なお,最大値を達成するマスの選び方が複数存在する場合,どれを出力してもよい.
入力例 1
3 1 5 3 2 1 4 8 7 6 9
出力例 1
19 X.. ..X .X.
入力例 2
3 2 10 10 1 10 10 1 1 1 10
出力例 2
50 XX. XX. ..X
Score : 100 points
Problem Statement
You are given a grid of N rows and M columns. The square at the i-th row and j-th column will be denoted as (i,j). A nonnegative integer A_{i,j} is written for each square (i,j).
You choose some of the squares so that each row and column contains at most K chosen squares. Under this constraint, calculate the maximum value of the sum of the integers written on the chosen squares. Additionally, calculate a way to choose squares that acheives the maximum.
Constraints
- 1 \leq N \leq 50
- 1 \leq K \leq N
- 0 \leq A_{i,j} \leq 10^9
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N K
A_{1,1} A_{1,2} \cdots A_{1,N}
A_{2,1} A_{2,2} \cdots A_{2,N}
\vdots
A_{N,1} A_{N,2} \cdots A_{N,N}
Output
On the first line, print the maximum value of the sum of the integers written on the chosen squares.
On the next N lines, print a way that achieves the maximum.
Precisely, output the strings t_1,t_2,\cdots,t_N, that satisfies t_{i,j}=X if you choose (i,j) and t_{i,j}=. otherwise.
You may print any way to choose squares that maximizes the sum.
Sample Input 1
3 1 5 3 2 1 4 8 7 6 9
Sample Output 1
19 X.. ..X .X.
Sample Input 2
3 2 10 10 1 10 10 1 1 1 10
Sample Output 2
50 XX. XX. ..X
実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
整数列 a_0, a_1, ..., a_{N - 1}、b_0, b_1, ..., b_{M - 1} が与えられます。整数列 c_0, c_1, ..., c_{(N - 1) + (M - 1)} を求めてください。
ただし、c_i = \sum_{j = 0}^i a_j b_{i - j} \bmod 998244353
です
制約
- 1 \leq N, M \leq 524288
- 0 \leq a_i, b_i < 998244353
入力
N M
a_0 a_1 ... a_{N-1}
b_0 b_1 ... b_{M-1}
出力
c_0 c_1 ... c_{(N - 1) + (M - 1)}
入力例 1
4 5 1 2 3 4 5 6 7 8 9
出力例 1
5 16 34 60 70 70 59 36
入力例 2
1 1 10000000 10000000
出力例 2
871938225
Score : 100 points
Problem Statement
You are given two integer arrays a_0, a_1, ..., a_{N - 1} and b_0, b_1, ..., b_{M - 1}. Calculate the array c_0, c_1, ..., c_{(N - 1) + (M - 1)}, defined by c_i = \sum_{j = 0}^i a_j b_{i - j} \bmod 998244353.
Constraints
- 1 \leq N, M \leq 524288
- 0 \leq a_i, b_i < 998244353
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N M
a_0 a_1 ... a_{N-1}
b_0 b_1 ... b_{M-1}
Output
Print the answer in the following format:
c_0 c_1 ... c_{(N - 1) + (M - 1)}
Sample Input 1
4 5 1 2 3 4 5 6 7 8 9
Sample Output 1
5 16 34 60 70 70 59 36
Sample Input 2
1 1 10000000 10000000
Sample Output 2
871938225
出典
Based on Library Checker (Convolution) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 頂点 M 辺の有向グラフが与えられる。i 番目の辺は (a_i, b_i) である。このグラフは単純とは限らない。 このグラフを強連結成分分解し、トポロジカルソートして出力してください。
制約
- 1 \leq N \leq 500,000
- 1 \leq M \leq 500,000
- 0 \leq a_i, b_i < N
入力
N M
a_0 b_0
a_1 b_1
:
a_{M - 1} b_{M - 1}
出力
K を強連結成分の行数として、1 + K 行出力する。 最初の行には K を出力し、その後 K 行では以下のように出力する。l は強連結成分の頂点数であり、v_i はその頂点番号である。
l v_0 v_1 ... v_{l-1}
ここで、各辺 (a_i, b_i) について、b_i が a_i より 先の行 に出現してはならない。
なお、正しい出力が複数存在する場合は、どれを出力しても構わない
入力例 1
6 7 1 4 5 2 3 0 5 5 4 1 0 3 4 2
出力例 1
4 1 5 2 4 1 1 2 2 3 0
Score : 100 points
Problem Statement
You are given a directed graph with N vertices and M edges, not necessarily simple. The i-th edge is oriented from the vertex a_i to the vertex b_i. Divide this graph into strongly connected components and print them in their topological order.
Constraints
- 1 \leq N \leq 500,000
- 1 \leq M \leq 500,000
- 0 \leq a_i, b_i < N
Input
Input is given from Standard Input in the following format:
N M
a_0 b_0
a_1 b_1
:
a_{M - 1} b_{M - 1}
Output
Print 1+K lines, where K is the number of strongly connected components. Print K on the first line. Print the information of each strongly connected component in next K lines in the following format, where l is the number of vertices in the strongly connected component and v_i is the index of the vertex in it.
l v_0 v_1 ... v_{l-1}
Here, for each edge (a_i, b_i), b_i should not appear in earlier line than a_i.
If there are multiple correct output, print any of them.
Sample Input 1
6 7 1 4 5 2 3 0 5 5 4 1 0 3 4 2
Sample Output 1
4 1 5 2 4 1 1 2 2 3 0
出典
Based on Library Checker (Strongly Connected Components) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
1 から N までの番号のついた N 本の旗があります. これらの旗を,数直線状に設置します.
旗 i は,座標 X_i または 座標 Y_i に設置することができます. ただし,どの 2 つの旗についても,その間の距離が D 以上である必要があります.
N 本の旗を設置することが可能かどうか判定し,可能であるならば,実際に置き方を 1 つ示してください.
制約
- 1 \leq N \leq 1000
- 0 \leq D \leq 10^9
- 0 \leq X_i < Y_i \leq 10^9
- 入力される数は全て整数である.
入力
入力は以下の形式で標準入力から与えられる.
N D X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
出力
N 本の旗を設置することが不可能な場合,No と出力せよ.
可能な場合,まず Yes と出力せよ.
そして,続いて N 行出力せよ.
このうち i 行目には,旗 i を設置する座標を出力せよ.
入力例 1
3 2 1 4 2 5 0 6
出力例 1
Yes 4 2 0
入力例 2
3 3 1 4 2 5 0 6
出力例 2
No
Score : 100 points
Problem Statement
Consider placing N flags on a line. Flags are numbered through 1 to N.
Flag i can be placed on the coordinate X_i or Y_i. For any two different flags, the distance between them should be at least D.
Decide whether it is possible to place all N flags. If it is possible, print such a configulation.
Constraints
- 1 \leq N \leq 1000
- 0 \leq D \leq 10^9
- 0 \leq X_i < Y_i \leq 10^9
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N D X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
Output
Print No if it is impossible to place N flags.
If it is possible, print Yes first.
After that, print N lines. i-th line of them should contain the coodinate of flag i.
Sample Input 1
3 2 1 4 2 5 0 6
Sample Output 1
Yes 4 2 0
Sample Input 2
3 3 1 4 2 5 0 6
Sample Output 2
No
実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
長さ N の文字列 S が与えられます。S の相異なる部分文字列の個数を求めてください。
制約
- 1 \leq N \leq 500,000
- S は英小文字からなる。
入力
S
出力
答えを一行に出力してください。
入力例 1
abcbcba
出力例 1
21
入力例 2
mississippi
出力例 2
53
入力例 3
ababacaca
出力例 3
33
入力例 4
aaaaa
出力例 4
5
Score : 100 points
Problem Statement
You are given a string of length N. Calculate the number of distinct substrings of S.
Constraints
- 1 \leq N \leq 500,000
- S consists of lowercase English letters.
Input
Input is given from Standard Input in the following format:
S
Output
Print the answer.
Sample Input 1
abcbcba
Sample Output 1
21
Sample Input 2
mississippi
Sample Output 2
53
Sample Input 3
ababacaca
Sample Output 3
33
Sample Input 4
aaaaa
Sample Output 4
5
出典
Based on Library Checker (Number of Substrings) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
長さ N の整数列 A=(A_1,A_2,\cdots,A_N) があります.
この数列に対して,Q 個のクエリを処理してください. i 番目のクエリでは,まず整数 T_i が与えられます. その後,T_i に応じて以下の操作を行ってください.
- T_i=1: 整数 X_i,V_i が与えられる.A_{X_i} を V_i で置き換える.
- T_i=2: 整数 L_i,R_i が与えられる.A_{L_i},A_{L_i+1},\cdots,A_{R_i} の中での最大値を求める.
- T_i=3: 整数 X_i,V_i が与えられる.X_i \leq j \leq N, V_i \leq A_j を満たす最小の j を求める. そのような j が存在しない場合,j=N+1 と答える.
制約
- 1 \leq N \leq 2 \times 10^5
- 0 \leq A_i \leq 10^9
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_i \leq 3
- 1 \leq X_i \leq N, 0 \leq V_i \leq 10^9 (T_i=1,3)
- 1 \leq L_i \leq R_i \leq N (T_i=2)
- 入力される数は全て整数である.
入力
入力は以下の形式で標準入力から与えられる.
N Q A_1 A_2 \cdots A_N 1 番目のクエリの情報 2 番目のクエリの情報 \vdots Q 番目のクエリの情報
各クエリの情報は,以下の形式で与えられる.
T_i=1,3 の場合
T_i X_i V_i
T_i=2 の場合
T_i L_i R_i
出力
T_i=2,3 のクエリについて,その答えを出力せよ.
入力例 1
5 5 1 2 3 2 1 2 1 5 3 2 3 1 3 1 2 2 4 3 1 3
出力例 1
3 3 2 6
- 1 番目のクエリ: (A_1,A_2,A_3,A_4,A_5)=(1,2,3,2,1) の最大値である,3 を出力する.
- 2 番目のクエリ: 3>A_2 なので,j=2 は不適.3 \leq A_3 なので,j=3 を出力する.
- 3 番目のクエリ: A_3 を 1 で置き換える.A=(1,2,1,2,1) になる.
- 4 番目のクエリ: (A_2,A_3,A_4)=(2,1,2) の最大値である,2 を出力する.
- 5 番目のクエリ: 条件を満たす j が存在しないので,j=N+1=6 を出力する.
Score : 100 points
Problem Statement
You are given an array a_0, a_1, ..., a_{N-1} of length N. Process Q queries of the following types.
The type of i-th query is represented by T_i.
- T_i=1: You are given two integers X_i,V_i. Replace the value of A_{X_i} with V_i.
- T_i=2: You are given two integers L_i,R_i. Calculate the maximum value among A_{L_i},A_{L_i+1},\cdots,A_{R_i}.
- T_i=3: You are given two integers X_i,V_i. Calculate the minimum j such that X_i \leq j \leq N, V_i \leq A_j. If there is no such j, answer j=N+1 instead.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 0 \leq A_i \leq 10^9
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_i \leq 3
- 1 \leq X_i \leq N, 0 \leq V_i \leq 10^9 (T_i=1,3)
- 1 \leq L_i \leq R_i \leq N (T_i=2)
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N Q A_1 A_2 \cdots A_N First query Second query \vdots Q-th query
Each query is given in the following format:
If T_i=1,3,
T_i X_i V_i
If T_i=2,
T_i L_i R_i
Output
For each query with T_i=2, 3, print the answer.
Sample Input 1
5 5 1 2 3 2 1 2 1 5 3 2 3 1 3 1 2 2 4 3 1 3
Sample Output 1
3 3 2 6
- First query: Print 3, which is the maximum of (A_1,A_2,A_3,A_4,A_5)=(1,2,3,2,1).
- Second query: Since 3>A_2, j=2 does not satisfy the condition.Since 3 \leq A_3, print j=3.
- Third query: Replace the value of A_3 with 1. It becomes A=(1,2,1,2,1).
- Fourth query: Print 2, which is the maximum of (A_2,A_3,A_4)=(2,1,2).
- Fifth query: Since there is no j that satisfies the condition, print j=N+1=6.
実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
長さ N の整数列 a_0, a_1, \dots, a_{N - 1} が与えられる。Q 個のクエリが飛んできます。処理してください。
0 l r b c: 各 i = l, l+1, \dots, {r - 1} について、a_i \gets b \times a_i + c1 l r: \sum_{i = l}^{r - 1} a_i \bmod 998244353 を出力する。
制約
- 1 \leq N, Q \leq 500000
- 0 \leq a_i, c < 998244353
- 1 \leq b < 998244353
- 0 \leq l < r \leq N
入力
N Q
a_0 a_1 ... a_{N - 1}
\textrm{Query}_0
\textrm{Query}_1
:
\textrm{Query}_{Q - 1}
出力
クエリ 1 ごとに各行に出力してください。
入力例 1
5 7 1 2 3 4 5 1 0 5 0 2 4 100 101 1 0 3 0 1 3 102 103 1 2 5 0 2 5 104 105 1 0 5
出力例 1
15 404 41511 4317767
Score : 100 points
Problem Statement
You are given an array a_0, a_1, ..., a_{N-1} of length N. Process Q queries of the following types.
0 l r b c: For each i = l, l+1, \dots, {r - 1}, set a_i \gets b \times a_i + c.1 l r: Print \sum_{i = l}^{r - 1} a_i \bmod 998244353.
Constraints
- 1 \leq N, Q \leq 500000
- 0 \leq a_i, c < 998244353
- 1 \leq b < 998244353
- 0 \leq l < r \leq N
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N Q
a_0 a_1 ... a_{N - 1}
\textrm{Query}_0
\textrm{Query}_1
:
\textrm{Query}_{Q - 1}
Output
For each query of the latter type, print the answer.
Sample Input 1
5 7 1 2 3 4 5 1 0 5 0 2 4 100 101 1 0 3 0 1 3 102 103 1 2 5 0 2 5 104 105 1 0 5
Sample Output 1
15 404 41511 4317767
出典
Based on Library Checker (Range Affine Range Sum) (APACHE LICENSE, V2.0)実行時間制限: 5 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
長さ N の整数列 A=(A_1,A_2,\cdots,A_N) があります. ここで,A の要素は全て 0 または 1 です.
この数列に対して,Q 個のクエリを処理してください. i 番目のクエリでは,整数 T_i,L_i,R_i が与えられます. その後,T_i に応じて以下の操作を行ってください.
- T_i=1: 各 L_i \leq j \leq R_i について,A_j を 1-A_j で置き換える.
- T_i=2: 整数列 A_{L_i},A_{L_i+1},\cdots,A_{R_i} の転倒数(※)を求める.
注釈:数列 x_1,x_2,\cdots,x_k の転倒数とは, 整数の組 i,j であって,1 \leq i < j \leq k, x_i > x_j を満たすものの数のことです.
制約
- 1 \leq N \leq 2 \times 10^5
- 0 \leq A_i \leq 1
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_i \leq 2
- 1 \leq L_i \leq R_i \leq N
- 入力される数は全て整数である.
入力
入力は以下の形式で標準入力から与えられる.
N Q A_1 A_2 \cdots A_N T_1 L_1 R_1 T_2 L_2 R_2 \vdots T_Q L_Q R_Q
出力
T_i=2 のクエリについて,その答えを出力せよ.
入力例 1
5 5 0 1 0 0 1 2 1 5 1 3 4 2 2 5 1 1 3 2 1 2
出力例 1
2 0 1
- 1 番目のクエリ: (A_1,A_2,A_3,A_4,A_5)=(0,1,0,0,1) の転倒数である,2 を出力する.
- 2 番目のクエリ: A_3 を 1 で置き換え,A_4 を 1 で置き換える.
- 3 番目のクエリ: (A_2,A_3,A_4,A_5)=(1,1,1,1) の転倒数である,0 を出力する.
- 4 番目のクエリ: A_1 を 1 で置き換え,A_2 を 0 で置き換え,A_3 を 0 で置き換える.
- 5 番目のクエリ: (A_1,A_2)=(1,0) の転倒数である,1 を出力する.
Score : 100 points
Problem Statement
You are given a binary array A=(A_1,A_2,\cdots,A_N) of length N.
Process Q queries of the following types. The i-th query is represented by three integers T_i,L_i,R_i.
- T_i=1: Replace the value of A_j with 1-A_j for each L_i \leq j \leq R_i.
- T_i=2: Calculate the inversion(*) of the array A_{L_i},A_{L_i+1},\cdots,A_{R_i}.
Note:The inversion of the array x_1,x_2,\cdots,x_k is the number of the pair of integers i,j with 1 \leq i < j \leq k, x_i > x_j.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 0 \leq A_i \leq 1
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_i \leq 2
- 1 \leq L_i \leq R_i \leq N
- All values in Input are integer.
Input
Input is given from Standard Input in the following format:
N Q A_1 A_2 \cdots A_N T_1 L_1 R_1 T_2 L_2 R_2 \vdots T_Q L_Q R_Q
Output
For each query with T_i=2, print the answer.
Sample Input 1
5 5 0 1 0 0 1 2 1 5 1 3 4 2 2 5 1 1 3 2 1 2
Sample Output 1
2 0 1
- First query: Print 2, which is the inversion of (A_1,A_2,A_3,A_4,A_5)=(0,1,0,0,1).
- Second query: Replace the value of A_3 and A_4 with 1 and 1, respectively.
- Third query: Print 0, which is the inversion of (A_2,A_3,A_4,A_5)=(1,1,1,1).
- Fourth query: Replace the value of A_1, A_2 and A_4 with 1, 0 and 0, respectively.
- Fifth query: Print 1, which is the inversion of (A_1,A_2)=(1,0).
実行時間制限: 10 sec / メモリ制限: 2500 MiB
配点 : 100 点
問題文
各言語でのメモリ使用量の確認と、ジャッジの MLE の挙動確認のための問題です。 サンプルケースを除き全部で 14 ケースありますが、最後のケースは AC できないことを想定しています。
p = 998244353 とおきます。 また、整数 N, K, x, y が与えられます。
数列 a_0, a_1, a_2, \ldots, a_{N-1} の一般項 a_n を次のように定義します。
- a_0 = x
- a_1 = y
- n \geq 2 のとき、 a_n = (a_{n-1} + a_{n-2} \cdot a_{\max (n-K, 0) }) \mod p
次に、長さ Q の数列 b_0, \ldots, b_{Q-1} が与えられます。 数列 c_0, \ldots, c_{Q-1} の一般項 c_n を次のように定義します。
- c_0 = a_{b_0}
- n \geq 1 のとき、 c_n = a_{(b_n + c_{n-1}) \mod N}
c_0, \ldots, c_{Q-1} を出力してください。
制約
- 1 \leq K \leq N \leq 7 \times 10^8
- (サンプルケースを除き) n ケース目では N=n \times (5 \times 10^7)
- 0 \leq x, y < 998244353
- 1 \leq Q \leq 10^6
- 0 \leq b_i < N
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N K x y
Q
b_0
:
b_{Q-1}
出力
出力は以下の形式で出力せよ。
c_0
:
c_{Q-1}
入力例 1
5 2 1 3 3 2 0 4
出力例 1
4 29 13
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
x 軸の正の向きが右、y 軸の正の向きが上であるような xy 座標平面において、点 (a,b) を原点を中心として反時計回りに d 度回転させた点を求めてください。
制約
- -1000 \leq a,b \leq 1000
- 1 \leq d \leq 360
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
a b d
出力
求めるべき点を (a',b') とするとき、 a' と b' をこの順に空白区切りで出力せよ。
なお、各出力について、解との絶対誤差または相対誤差が 10^{−6} 以下であれば正解として扱われる。
入力例 1
2 2 180
出力例 1
-2 -2
(2,2) を原点を中心として反時計回りに 180 度回転させた点は、(2,2) を原点について対称な位置に移動させた点であり、(-2,-2) となります。
入力例 2
5 0 120
出力例 2
-2.49999999999999911182 4.33012701892219364908
(5,0) を原点を中心として反時計回りに 120 度回転させた点は (-\frac {5}{2} , \frac {5\sqrt{3}}{2}) です。
この例での出力はこれらの値と厳密には一致しませんが、誤差が十分に小さいため正解として扱われます。
入力例 3
0 0 11
出力例 3
0.00000000000000000000 0.00000000000000000000
(a,b) が原点(回転の中心)なので回転させても座標が変わりません。
入力例 4
15 5 360
出力例 4
15.00000000000000177636 4.99999999999999555911
360 度回転させたので座標が変わりません。
入力例 5
-505 191 278
出力例 5
118.85878514480690171240 526.66743699786547949770
Score : 200 points
Problem Statement
In an xy-coordinate plane whose x-axis is oriented to the right and whose y-axis is oriented upwards, rotate a point (a, b) around the origin d degrees counterclockwise and find the new coordinates of the point.
Constraints
- -1000 \leq a,b \leq 1000
- 1 \leq d \leq 360
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
a b d
Output
Let the new coordinates of the point be (a', b'). Print a' and b' in this order, with a space in between.
Your output will be considered correct when, for each value printed, the absolute or relative error from the answer is at most 10^{-6}.
Sample Input 1
2 2 180
Sample Output 1
-2 -2
When (2, 2) is rotated around the origin 180 degrees counterclockwise, it becomes the symmetric point of (2, 2) with respect to the origin, which is (-2, -2).
Sample Input 2
5 0 120
Sample Output 2
-2.49999999999999911182 4.33012701892219364908
When (5, 0) is rotated around the origin 120 degrees counterclockwise, it becomes (-\frac {5}{2} , \frac {5\sqrt{3}}{2}).
This sample output does not precisely match these values, but the errors are small enough to be considered correct.
Sample Input 3
0 0 11
Sample Output 3
0.00000000000000000000 0.00000000000000000000
Since (a, b) is the origin (the center of rotation), a rotation does not change its coordinates.
Sample Input 4
15 5 360
Sample Output 4
15.00000000000000177636 4.99999999999999555911
A 360-degree rotation does not change the coordinates of a point.
Sample Input 5
-505 191 278
Sample Output 5
118.85878514480690171240 526.66743699786547949770
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
高橋君と青木君は 2 人で次の対戦ゲームをします。
高橋君が先手でゲームを始め、ゲームが終了するまでの間、 2 人は交互に 1 以上 2N+1 以下の整数を 1 つずつ宣言します。 どちらかが一度でも宣言した整数は、それ以降どちらも二度と宣言することが出来ません。 先に整数を宣言することが出来なくなった方のプレイヤーの負けとなり、負けなかった方のプレイヤーの勝ちとなります。
このゲームでは必ず高橋君が勝ちます。 高橋君の立場で実際にゲームを行い、ゲームに勝ってください。
制約
- 1 \leq N \leq 1000
- N は整数
入出力
この問題はインタラクティブな問題(あなたの作成したプログラムとジャッジプログラムが入出力を介して対話を行う形式の問題)です。
あなたのプログラムが高橋君の立場で、ジャッジプログラムが青木君の立場でゲームを行います。
まず、あなたのプログラムに標準入力から正の整数 N が与えられます。 その後、ゲームが終了するまで下記の手順を繰り返します。
- あなたのプログラムが、高橋君が宣言する整数として、1 以上 2N+1 以下の整数を標準出力に出力します。(どちらかのプレイヤーによってすでに宣言されている整数を出力することは出来ません。)
- ジャッジプログラムによって、青木君が宣言する整数があなたのプログラムに標準入力から与えられます。(どちらかのプレイヤーによってすでに宣言されている整数が入力されることはありません。) ただし、青木君が宣言できる整数が残っていない場合は、代わりに 0 が与えられ高橋君の勝ちでゲームが終了します。
注意点
- 出力を行うたびに標準出力をflushしてください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
- 高橋君の勝ちでゲームが終了したあと、あなたのプログラムは直ちに終了しなければなりません。そうしなかった場合、ジャッジ結果が AC とならない可能性があります。
- ゲームの途中で不正な出力を行った場合(例えば、すでにどちらかのプレイヤーによって宣言されている整数を出力した場合)は不正解となりますが、そのときのジャッジ結果は不定です。WA になるとは限りません。
入出力例
| 入力 | 出力 | 説明 |
|---|---|---|
| 2 | まず整数 N が与えられます。 | |
| 1 | 高橋君が 1 を宣言します。 | |
| 3 | 青木君が 3 を宣言します。 | |
| 2 | 高橋君が 2 を宣言します。 | |
| 4 | 青木君が 4 を宣言します。 | |
| 5 | 高橋君が 5 を宣言します。 | |
| 0 | 青木君が宣言できる整数が残っていないため、高橋君の勝ちでゲームが終了します。 |
Score : 300 points
Problem Statement
Takahashi and Aoki will play the following game against each other.
Starting from Takahashi, the two alternatingly declare an integer between 1 and 2N+1 (inclusive) until the game ends. Any integer declared by either player cannot be declared by either player again. The player who is no longer able to declare an integer loses; the player who didn't lose wins.
In this game, Takahashi will always win. Your task is to actually play the game on behalf of Takahashi and win the game.
Constraints
- 1 \leq N \leq 1000
- N is an integer.
Input and Output
This task is an interactive task (in which your program and the judge program interact with each other via inputs and outputs).
Your program plays the game on behalf of Takahashi, and the judge program plays the game on behalf of Aoki.
First, your program is given a positive integer N from Standard Input. Then, the following procedures are repeated until the game ends.
- Your program outputs an integer between 1 and 2N+1 (inclusive) to Standard Output, which defines the integer that Takahashi declares. (You cannot output an integer that is already declared by either player.)
- The integer that Aoki declares is given by the judge program to your program from Standard Input. (No integer that is already declared by either player will be given.) If Aoki has no more integer to declare, 0 is given instead, which means that the game ended and Takahashi won.
Notes
- After each output, you must flush Standard Output. Otherwise, you may get TLE.
- After the game ended and Takahashi won, the program must be terminated immediately. Otherwise, the judge does not necessarily give AC.
- If your program outputs something that violates the rules of the game (such as an integer that has already been declared by either player), your answer is considered incorrect. In such case, the verdict is indeterminate. It does not necessarily give WA.
Sample Input and Output
| Input | Output | Description |
|---|---|---|
| 2 | First, an integer N is given. | |
| 1 | Takahashi declares an integer 1. | |
| 3 | Aoki declares an integer 3. | |
| 2 | Takahashi declares an integer 2. | |
| 4 | Aoki declares an integer 4. | |
| 5 | Takahashi declares an integer 5. | |
| 0 | Aoki has no more integer to declare, so Takahashi wins, and the game ends. |
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
N 個の整数 A_1,...,A_N が与えられます。
A_1 \times ... \times A_N を求めてください。
ただし、結果が 10^{18} を超える場合は、代わりに -1 を出力してください。
制約
- 2 \leq N \leq 10^5
- 0 \leq A_i \leq 10^{18}
- 入力は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 ... A_N
出力
値 A_1 \times ... \times A_N を整数として出力せよ。ただし、この値が 10^{18} を超える場合は、代わりに -1 を出力せよ。
入力例 1
2 1000000000 1000000000
出力例 1
1000000000000000000
1000000000 \times 1000000000 = 1000000000000000000 です。
入力例 2
3 101 9901 999999000001
出力例 2
-1
101 \times 9901 \times 999999000001 = 1000000000000000001 ですが、これは 10^{18} を超えるので、代わりに -1 を出力します。
入力例 3
31 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0
出力例 3
0
Score : 200 points
Problem Statement
Given N integers A_1, ..., A_N, compute A_1 \times ... \times A_N.
However, if the result exceeds 10^{18}, print -1 instead.
Constraints
- 2 \leq N \leq 10^5
- 0 \leq A_i \leq 10^{18}
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N A_1 ... A_N
Output
Print the value A_1 \times ... \times A_N as an integer, or -1 if the value exceeds 10^{18}.
Sample Input 1
2 1000000000 1000000000
Sample Output 1
1000000000000000000
We have 1000000000 \times 1000000000 = 1000000000000000000.
Sample Input 2
3 101 9901 999999000001
Sample Output 2
-1
We have 101 \times 9901 \times 999999000001 = 1000000000000000001, which exceeds 10^{18}, so we should print -1 instead.
Sample Input 3
31 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0
Sample Output 3
0
実行時間制限: 12 sec / メモリ制限: 1024 MiB
配点 : 675 点
問題文
マス 0, マス 1, \dots, マス N の N+1 個のマスからなるスゴロクがあります。
また、1 以上 K 以下の整数が等確率で出るサイコロがあります。
はじめ、あなたはマス 0 にいます。あなたはマス N に着くまで次の操作を繰り返します。
- サイコロを振る。今いるマスを x 、サイコロで出た整数を y としてマス \min(N, x + y) に移動する。
ちょうど i 回の操作によってマス N に着く確率を P_i とします。P_1, P_2, \dots, P_N を \text{mod }998244353 で計算してください。
確率 \text{mod }998244353 とは
求める確率は必ず有理数となることが証明できます。 またこの問題の制約下では、その値を互いに素な 2 つの整数 P, Q を用いて \frac{P}{Q} と表したとき、R \times Q \equiv P\pmod{998244353} かつ 0 \leq R \lt 998244353 を満たす整数 R がただ一つ存在することが証明できます。この R を求めてください。制約
- 1 \leq K \leq N \leq 2 \times 10^5
- N, K は整数
入力
入力は以下の形式で標準入力から与えられる。
N K
出力
N 行出力せよ。i 行目には P_i を \text{mod }998244353 で出力せよ。
入力例 1
3 2
出力例 1
0 249561089 748683265
例えば、ちょうど 2 回の操作でマス N に辿り着くのは以下の整数がサイコロで出たときです。
- 1 回目の操作で 1 が出て、2 回目の操作で 2 が出る
- 1 回目の操作で 2 が出て、2 回目の操作で 1 が出る
- 1 回目の操作で 2 が出て、2 回目の操作で 2 が出る
よって P_2 = \left( \frac{1}{2} \times \frac{1}{2} \right) \times 3 = \frac{3}{4} です。249561089 \times 4 \equiv 3 \pmod{998244353} なので 249561089 を P_2 として出力します。
入力例 2
5 5
出力例 2
598946612 479157290 463185380 682000542 771443236
入力例 3
10 6
出力例 3
0 166374059 207967574 610038216 177927813 630578223 902091444 412046453 481340945 404612686
Score: 675 points
Problem Statement
There is a board game with N+1 squares: square 0, square 1, \dots, square N.
You have a die (dice) that rolls an integer between 1 and K, inclusive, with equal probability for each outcome.
You start on square 0. You repeat the following operation until you reach square N:
- Roll the dice. Let x be the current square and y be the rolled number, then move to square \min(N, x + y).
Let P_i be the probability of reaching square N after exactly i operations. Calculate P_1, P_2, \dots, P_N modulo 998244353.
What is probability modulo 998244353?
It can be proved that the sought probabilities will always be rational numbers. Under the constraints of this problem, it can also be proved that when expressing the values as \frac{P}{Q} using two coprime integers P and Q, there is exactly one integer R satisfying R \times Q \equiv P\pmod{998244353} and 0 \leq R < 998244353. Find this R.Constraints
- 1 \leq K \leq N \leq 2 \times 10^5
- N and K are integers.
Input
The input is given from Standard Input in the following format:
N K
Output
Print N lines. The i-th line should contain P_i modulo 998244353.
Sample Input 1
3 2
Sample Output 1
0 249561089 748683265
For example, you reach square N after exactly two operations when the die rolls the following numbers:
- A 1 on the first operation, and a 2 on the second operation.
- A 2 on the first operation, and a 1 on the second operation.
- A 2 on the first operation, and a 2 on the second operation.
Therefore, P_2 = \left( \frac{1}{2} \times \frac{1}{2} \right) \times 3 = \frac{3}{4}. We have 249561089 \times 4 \equiv 3 \pmod{998244353}, so print 249561089 for P_2.
Sample Input 2
5 5
Sample Output 2
598946612 479157290 463185380 682000542 771443236
Sample Input 3
10 6
Sample Output 3
0 166374059 207967574 610038216 177927813 630578223 902091444 412046453 481340945 404612686
実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
縦 H マス、横 W マスのグリッドがあります。上から i 行目、左から j 列目のマスを (i, j) と表します。
はじめ、全てのマスには壁が 1 個ずつ立てられています。
以下で説明されるクエリを Q 個与えられる順に処理した後に、残っている壁の個数を求めてください。
q 番目のクエリでは整数 R_q, C_q が与えられます。
あなたは (R_q, C_q) に爆弾を置いて壁を爆破します。その結果、以下の処理が行われます。
- (R_q, C_q) に壁が存在する場合は、その壁を破壊して処理を終了する。
- (R_q, C_q) に壁が存在しない場合は、(R_q, C_q) から上下左右に見て最初に現れる壁を破壊する。厳密に述べると、以下の 4 個の処理が同時に行われる。
- (i, C_q) に壁が存在して (k, C_q) (i \lt k \lt R_q) に壁が存在しないような i \lt R_q が存在する時、(i, C_q) に存在する壁を破壊する。
- (i, C_q) に壁が存在して (k, C_q) (R_q \lt k \lt i) に壁が存在しないような i \gt R_q が存在する時、(i, C_q) に存在する壁を破壊する。
- (R_q, j) に壁が存在して (R_q, k) (j \lt k \lt C_q) に壁が存在しないような j \lt C_q が存在する時、(R_q, j) に存在する壁を破壊する。
- (R_q, j) に壁が存在して (R_q, k) (C_q \lt k \lt j) に壁が存在しないような j \gt C_q が存在する時、(R_q, j) に存在する壁を破壊する。
制約
- 1 \leq H, W
- H \times W \leq 4 \times 10^5
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq R_q \leq H
- 1 \leq C_q \leq W
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
H W Q R_1 C_1 R_2 C_2 \vdots R_Q C_Q
出力
クエリを全て処理した後に、残っている壁の個数を出力せよ。
入力例 1
2 4 3 1 2 1 2 1 3
出力例 1
2
クエリを処理する手順を説明すると次のようになります。
- 1 番目のクエリでは (R_1, C_1) = (1, 2) である。 (1, 2) に壁は存在するので (1, 2) の壁が爆破される。
- 2 番目のクエリでは (R_2, C_2) = (1, 2) である。 (1, 2) に壁は存在しないので、(1, 2) から上下左右に見て最初に現れる壁である (2,2),(1,1),(1,3) が爆破される。
- 3 番目のクエリでは (R_2, C_2) = (1, 3) である。 (1, 3) に壁は存在しないので、(1, 3) から上下左右に見て最初に現れる壁である (2,3),(1,4) が爆破される。
全てのクエリを処理した後に残っている壁は (2, 1), (2, 4) の 2 個です。
入力例 2
5 5 5 3 3 3 3 3 2 2 2 1 2
出力例 2
10
入力例 3
4 3 10 2 2 4 1 1 1 4 2 2 1 3 1 1 3 1 2 4 3 4 2
出力例 3
2
Score : 400 points
Problem Statement
There is a grid with H rows and W columns. Let (i, j) denote the cell at the i-th row from the top and j-th column from the left.
Initially, there is one wall in each cell.
After processing Q queries explained below in the order they are given, find the number of remaining walls.
In the q-th query, you are given two integers R_q and C_q.
You place a bomb at (R_q, C_q) to destroy walls. As a result, the following process occurs.
- If there is a wall at (R_q, C_q), destroy that wall and end the process.
- If there is no wall at (R_q, C_q), destroy the first walls that appear when looking up, down, left, and right from (R_q, C_q). More precisely, the following four processes occur simultaneously:
- If there exists an i \lt R_q such that a wall exists at (i, C_q) and no wall exists at (k, C_q) for all i \lt k \lt R_q, destroy the wall at (i, C_q).
- If there exists an i \gt R_q such that a wall exists at (i, C_q) and no wall exists at (k, C_q) for all R_q \lt k \lt i, destroy the wall at (i, C_q).
- If there exists a j \lt C_q such that a wall exists at (R_q, j) and no wall exists at (R_q, k) for all j \lt k \lt C_q, destroy the wall at (R_q, j).
- If there exists a j \gt C_q such that a wall exists at (R_q, j) and no wall exists at (R_q, k) for all C_q \lt k \lt j, destroy the wall at (R_q, j).
Constraints
- 1 \leq H, W
- H \times W \leq 4 \times 10^5
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq R_q \leq H
- 1 \leq C_q \leq W
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H W Q R_1 C_1 R_2 C_2 \vdots R_Q C_Q
Output
Print the number of remaining walls after processing all queries.
Sample Input 1
2 4 3 1 2 1 2 1 3
Sample Output 1
2
The process of handling the queries can be explained as follows:
- In the 1st query, (R_1, C_1) = (1, 2). There is a wall at (1, 2), so the wall at (1, 2) is destroyed.
- In the 2nd query, (R_2, C_2) = (1, 2). There is no wall at (1, 2), so the walls at (2,2),(1,1),(1,3), which are the first walls that appear when looking up, down, left, and right from (1, 2), are destroyed.
- In the 3rd query, (R_3, C_3) = (1, 3). There is no wall at (1, 3), so the walls at (2,3),(1,4), which are the first walls that appear when looking up, down, left, and right from (1, 3), are destroyed.
After processing all queries, there are two remaining walls, at (2, 1) and (2, 4).
Sample Input 2
5 5 5 3 3 3 3 3 2 2 2 1 2
Sample Output 2
10
Sample Input 3
4 3 10 2 2 4 1 1 1 4 2 2 1 3 1 1 3 1 2 4 3 4 2
Sample Output 3
2
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 350 点
問題文
AtCoder Land のお土産屋に N 個の箱が売られています。
箱には 1, 2, \ldots, N の番号が付いており、箱 i の価格は A_i 円であり、A_i 個のお菓子が入っています。
高橋君は N 個の箱のうち M 個の箱を選んで買って帰り、1, 2, \ldots, M の名前が付いた M 人の人に 1 つずつ箱を渡そうとしています。
ただし、高橋君は以下の条件を満たすことができるように箱を買いたいです。
- 各 i = 1, 2, \ldots, M について、人 i には B_i 個以上のお菓子が入った箱を渡す
1 人に 2 個以上の箱を渡すことや同じ箱を複数人に渡すことはできないことに注意してください。
適切に箱を M 個買うことで条件を満たすことができるか判定し、条件を満たすことができる場合は高橋君が支払う金額の合計の最小値を求めてください。
制約
- 1 \leq M \leq N \leq 2 \times 10^5
- 1 \leq A_i, B_i \leq 10^9
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 \ldots A_N B_1 B_2 \ldots B_M
出力
適切に箱を M 個買うことで条件を満たすことができる場合は高橋君が支払う金額の合計の最小値を出力せよ。そうでない場合は -1 を出力せよ。
入力例 1
4 2 3 4 5 4 1 4
出力例 1
7
高橋君は箱 1, 4 を買い、箱 1 を人 1、箱 4 を人 2 に渡すことで条件を満たすことができます。
このとき高橋君が支払う金額の合計は 7 円であり、支払う金額が 7 円未満のときは条件を満たすことはできないため、7 を出力します。
入力例 2
3 3 1 1 1 1000000000 1000000000 1000000000
出力例 2
-1
入力例 3
7 3 2 6 8 9 5 1 11 3 5 7
出力例 3
19
Score : 350 points
Problem Statement
A souvenir shop at AtCoder Land sells N boxes.
The boxes are numbered 1 to N, and box i has a price of A_i yen and contains A_i pieces of candy.
Takahashi wants to buy M out of the N boxes and give one box each to M people named 1, 2, \ldots, M.
Here, he wants to buy boxes that can satisfy the following condition:
- For each i = 1, 2, \ldots, M, person i is given a box containing at least B_i pieces of candy.
Note that it is not allowed to give more than one box to a single person or to give the same box to multiple people.
Determine whether it is possible to buy M boxes that can satisfy the condition, and if it is possible, find the minimum total amount of money Takahashi needs to pay.
Constraints
- 1 \leq M \leq N \leq 2 \times 10^5
- 1 \leq A_i, B_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 A_2 \ldots A_N B_1 B_2 \ldots B_M
Output
If it is possible to buy M boxes that can satisfy the condition, print the minimum total amount of money Takahashi needs to pay. Otherwise, print -1.
Sample Input 1
4 2 3 4 5 4 1 4
Sample Output 1
7
Takahashi can buy boxes 1 and 4, and give box 1 to person 1 and box 4 to person 2 to satisfy the condition.
In this case, he needs to pay 7 yen in total, and it is impossible to satisfy the condition by paying less than 7 yen, so print 7.
Sample Input 2
3 3 1 1 1 1000000000 1000000000 1000000000
Sample Output 2
-1
Sample Input 3
7 3 2 6 8 9 5 1 11 3 5 7
Sample Output 3
19
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
2次元平面上の N 点 (X_1,Y_1),\ldots,(X_N,Y_N) に家が建っています。
最初、点 (S_x,S_y) にサンタクロースがいます。サンタクロースは列 (D_1,C_1),\ldots,(D_M,C_M) に従って以下の行動を行います。
- i=1,2,\ldots,M の順に以下のように移動する。
- 現在サンタクロースがいる点を (x,y) とする。
- D_i が
Uなら、(x,y) から (x,y+C_i) に直線で移動する。 - D_i が
Dなら、(x,y) から (x,y-C_i) に直線で移動する。 - D_i が
Lなら、(x,y) から (x-C_i,y) に直線で移動する。 - D_i が
Rなら、(x,y) から (x+C_i,y) に直線で移動する。
- D_i が
- 現在サンタクロースがいる点を (x,y) とする。
行動を終えたあとにサンタクロースがいる点と、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。
制約
- 1 \leq N \leq 2\times 10^5
- 1 \leq M \leq 2\times 10^5
- -10^9 \leq X_i,Y_i \leq 10^9
- (X_i,Y_i) は相異なる
- -10^9 \leq S_x,S_y \leq 10^9
- (S_x,S_y) に家は建っていない
- D_i は
U,D,L,Rのいずれかである - 1 \leq C_i \leq 10^9
- 与えられる数値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M S_x S_y X_1 Y_1 \vdots X_N Y_N D_1 C_1 \vdots D_M C_M
出力
行動を終えたあとサンタクロースがいる点を (X,Y)、行動により通過または到達した家の数を C とするとき、X,Y,C をこの順に空白区切りで出力せよ。
入力例 1
3 4 3 2 2 2 3 3 2 1 L 2 D 1 R 1 U 2
出力例 1
2 3 2
サンタクロースは以下のように行動します。
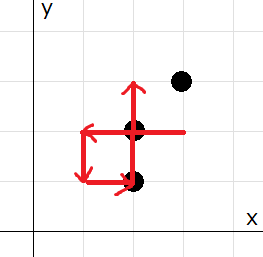
- D_1=
Lなので (3,2) から (3-2,2) に直線で移動する。このとき (2,2) に建っている家を通過する。 - D_2=
Dなので (1,2) から (1,2-1) に直線で移動する。 - D_3=
Rなので (1,1) から (1+1,1) に直線で移動する。このとき (2,1) に建っている家を通過する。 - D_4=
Uなので (2,1) から (2,1+2) に直線で移動する。このとき (2,2) に建っている家を通過するが、この家はすでに通過したことがある家である。
行動により通過または到達した家の数は 2 です。
入力例 2
1 3 0 0 1 1 R 1000000000 R 1000000000 R 1000000000
出力例 2
3000000000 0 0
オーバーフローに注意してください。
Score : 425 points
Problem Statement
There are N houses at points (X_1,Y_1),\ldots,(X_N,Y_N) on a two-dimensional plane.
Initially, Santa Claus is at point (S_x,S_y). He will act according to the sequence (D_1,C_1),\ldots,(D_M,C_M) as follows:
- For i=1,2,\ldots,M in order, he moves as follows:
- Let (x,y) be the point where he currently is.
- If D_i is
U, move in a straight line from (x,y) to (x,y+C_i). - If D_i is
D, move in a straight line from (x,y) to (x,y-C_i). - If D_i is
L, move in a straight line from (x,y) to (x-C_i,y). - If D_i is
R, move in a straight line from (x,y) to (x+C_i,y).
- If D_i is
- Let (x,y) be the point where he currently is.
Find the point where he is after completing all actions, and the number of distinct houses he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.
Constraints
- 1 \leq N \leq 2\times 10^5
- 1 \leq M \leq 2\times 10^5
- -10^9 \leq X_i,Y_i \leq 10^9
- The pairs (X_i,Y_i) are distinct.
- -10^9 \leq S_x,S_y \leq 10^9
- There is no house at (S_x,S_y).
- Each D_i is one of
U,D,L,R. - 1 \leq C_i \leq 10^9
- All input numbers are integers.
Input
The input is given from Standard Input in the following format:
N M S_x S_y X_1 Y_1 \vdots X_N Y_N D_1 C_1 \vdots D_M C_M
Output
Let (X,Y) be the point where he is after completing all actions, and C be the number of distinct houses passed through or arrived at. Print X,Y,C in this order separated by spaces.
Sample Input 1
3 4 3 2 2 2 3 3 2 1 L 2 D 1 R 1 U 2
Sample Output 1
2 3 2
Santa Claus behaves as follows:

- D_1=
L, so he moves from (3,2) to (3-2,2) in a straight line. During this, he passes through the house at (2,2). - D_2=
D, so he moves from (1,2) to (1,2-1) in a straight line. - D_3=
R, so he moves from (1,1) to (1+1,1) in a straight line. During this, he passes through the house at (2,1). - D_4=
U, so he moves from (2,1) to (2,1+2) in a straight line. During this, he passes through the house at (2,2), but it has already been passed.
The number of houses he passed or arrived during his actions is 2.
Sample Input 2
1 3 0 0 1 1 R 1000000000 R 1000000000 R 1000000000
Sample Output 2
3000000000 0 0
Be careful with overflow.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 頂点 M 辺の有向グラフ G があります。 頂点には 1, 2, \ldots, N と番号が振られています。 各 i (1 \leq i \leq M) について、i 番目の有向辺は頂点 x_i から y_i へ張られています。 G は有向閉路を含みません。
G の有向パスのうち、最長のものの長さを求めてください。 ただし、有向パスの長さとは、有向パスに含まれる辺の本数のことです。
制約
- 入力はすべて整数である。
- 2 \leq N \leq 10^5
- 1 \leq M \leq 10^5
- 1 \leq x_i, y_i \leq N
- ペア (x_i, y_i) はすべて相異なる。
- G は有向閉路を含まない。
入力
入力は以下の形式で標準入力から与えられる。
N M x_1 y_1 x_2 y_2 : x_M y_M
出力
G の有向パスのうち、最長のものの長さを出力せよ。
入力例 1
4 5 1 2 1 3 3 2 2 4 3 4
出力例 1
3
次図の赤い有向パスが最長です。

入力例 2
6 3 2 3 4 5 5 6
出力例 2
2
次図の赤い有向パスが最長です。

入力例 3
5 8 5 3 2 3 2 4 5 2 5 1 1 4 4 3 1 3
出力例 3
3
例えば、次図の赤い有向パスが最長です。

Score : 100 points
Problem Statement
There is a directed graph G with N vertices and M edges. The vertices are numbered 1, 2, \ldots, N, and for each i (1 \leq i \leq M), the i-th directed edge goes from Vertex x_i to y_i. G does not contain directed cycles.
Find the length of the longest directed path in G. Here, the length of a directed path is the number of edges in it.
Constraints
- All values in input are integers.
- 2 \leq N \leq 10^5
- 1 \leq M \leq 10^5
- 1 \leq x_i, y_i \leq N
- All pairs (x_i, y_i) are distinct.
- G does not contain directed cycles.
Input
Input is given from Standard Input in the following format:
N M x_1 y_1 x_2 y_2 : x_M y_M
Output
Print the length of the longest directed path in G.
Sample Input 1
4 5 1 2 1 3 3 2 2 4 3 4
Sample Output 1
3
The red directed path in the following figure is the longest:

Sample Input 2
6 3 2 3 4 5 5 6
Sample Output 2
2
The red directed path in the following figure is the longest:

Sample Input 3
5 8 5 3 2 3 2 4 5 2 5 1 1 4 4 3 1 3
Sample Output 3
3
The red directed path in the following figure is one of the longest:

実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
N 枚の皿があります。 皿には 1, 2, \ldots, N と番号が振られています。 最初、各 i (1 \leq i \leq N) について、皿 i には a_i (1 \leq a_i \leq 3) 個の寿司が置かれています。
すべての寿司が無くなるまで、太郎君は次の操作を繰り返し行います。
- 1, 2, \ldots, N の目が等確率で出るサイコロを振り、出目を i とする。 皿 i に寿司がある場合、皿 i の寿司を 1 個食べる。 皿 i に寿司が無い場合、何も行わない。
すべての寿司が無くなるまでの操作回数の期待値を求めてください。
制約
- 入力はすべて整数である。
- 1 \leq N \leq 300
- 1 \leq a_i \leq 3
入力
入力は以下の形式で標準入力から与えられる。
N a_1 a_2 \ldots a_N
出力
すべての寿司が無くなるまでの操作回数の期待値を出力せよ。 相対誤差が 10^{-9} 以下ならば正解となる。
入力例 1
3 1 1 1
出力例 1
5.5
1 個目の寿司を食べるまでの操作回数の期待値は 1 です。 その後、2 個目の寿司を食べるまでの操作回数の期待値は 1.5 です。 その後、3 個目の寿司を食べるまでの操作回数の期待値は 3 です。 よって、全体の操作回数の期待値は 1 + 1.5 + 3 = 5.5 です。
入力例 2
1 3
出力例 2
3
例えば、3.00, 3.000000003, 2.999999997 などを出力しても正解となります。
入力例 3
2 1 2
出力例 3
4.5
入力例 4
10 1 3 2 3 3 2 3 2 1 3
出力例 4
54.48064457488221
Score : 100 points
Problem Statement
There are N dishes, numbered 1, 2, \ldots, N. Initially, for each i (1 \leq i \leq N), Dish i has a_i (1 \leq a_i \leq 3) pieces of sushi on it.
Taro will perform the following operation repeatedly until all the pieces of sushi are eaten:
- Roll a die that shows the numbers 1, 2, \ldots, N with equal probabilities, and let i be the outcome. If there are some pieces of sushi on Dish i, eat one of them; if there is none, do nothing.
Find the expected number of times the operation is performed before all the pieces of sushi are eaten.
Constraints
- All values in input are integers.
- 1 \leq N \leq 300
- 1 \leq a_i \leq 3
Input
Input is given from Standard Input in the following format:
N a_1 a_2 \ldots a_N
Output
Print the expected number of times the operation is performed before all the pieces of sushi are eaten. The output is considered correct when the relative difference is not greater than 10^{-9}.
Sample Input 1
3 1 1 1
Sample Output 1
5.5
The expected number of operations before the first piece of sushi is eaten, is 1. After that, the expected number of operations before the second sushi is eaten, is 1.5. After that, the expected number of operations before the third sushi is eaten, is 3. Thus, the expected total number of operations is 1 + 1.5 + 3 = 5.5.
Sample Input 2
1 3
Sample Output 2
3
Outputs such as 3.00, 3.000000003 and 2.999999997 will also be accepted.
Sample Input 3
2 1 2
Sample Output 3
4.5
Sample Input 4
10 1 3 2 3 3 2 3 2 1 3
Sample Output 4
54.48064457488221
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
太郎君と次郎君が次のゲームで勝負します。
最初に、数列 a = (a_1, a_2, \ldots, a_N) が与えられます。 a が空になるまで、二人は次の操作を交互に行います。 先手は太郎君です。
- a の先頭要素または末尾要素を取り除く。 取り除いた要素を x とすると、操作を行った人は x 点を得る。
ゲーム終了時の太郎君の総得点を X、次郎君の総得点を Y とします。 太郎君は X - Y を最大化しようとし、次郎君は X - Y を最小化しようとします。
二人が最適に行動すると仮定したとき、X - Y を求めてください。
制約
- 入力はすべて整数である。
- 1 \leq N \leq 3000
- 1 \leq a_i \leq 10^9
入力
入力は以下の形式で標準入力から与えられる。
N a_1 a_2 \ldots a_N
出力
二人が最適に行動すると仮定したとき、X - Y を出力せよ。
入力例 1
4 10 80 90 30
出力例 1
10
二人が最適に行動すると、次のように操作が行われます。 操作対象の要素を太字で表しています。
- 先手: (10, 80, 90, 30) → (10, 80, 90)
- 後手: (10, 80, 90) → (10, 80)
- 先手: (10, 80) → (10)
- 後手: (10) → ()
このとき、X = 30 + 80 = 110, Y = 90 + 10 = 100 となります。
入力例 2
3 10 100 10
出力例 2
-80
二人が最適に行動すると、例えば次のように操作が行われます。
- 先手: (10, 100, 10) → (100, 10)
- 後手: (100, 10) → (10)
- 先手: (10) → ()
このとき、X = 10 + 10 = 20, Y = 100 となります。
入力例 3
1 10
出力例 3
10
入力例 4
10 1000000000 1 1000000000 1 1000000000 1 1000000000 1 1000000000 1
出力例 4
4999999995
答えは 32-bit 整数型に収まらない場合があります。
入力例 5
6 4 2 9 7 1 5
出力例 5
2
二人が最適に行動すると、例えば次のように操作が行われます。
- 先手: (4, 2, 9, 7, 1, 5) → (4, 2, 9, 7, 1)
- 後手: (4, 2, 9, 7, 1) → (2, 9, 7, 1)
- 先手: (2, 9, 7, 1) → (2, 9, 7)
- 後手: (2, 9, 7) → (2, 9)
- 先手: (2, 9) → (2)
- 後手: (2) → ()
このとき、X = 5 + 1 + 9 = 15, Y = 4 + 7 + 2 = 13 となります。
Score : 100 points
Problem Statement
Taro and Jiro will play the following game against each other.
Initially, they are given a sequence a = (a_1, a_2, \ldots, a_N). Until a becomes empty, the two players perform the following operation alternately, starting from Taro:
- Remove the element at the beginning or the end of a. The player earns x points, where x is the removed element.
Let X and Y be Taro's and Jiro's total score at the end of the game, respectively. Taro tries to maximize X - Y, while Jiro tries to minimize X - Y.
Assuming that the two players play optimally, find the resulting value of X - Y.
Constraints
- All values in input are integers.
- 1 \leq N \leq 3000
- 1 \leq a_i \leq 10^9
Input
Input is given from Standard Input in the following format:
N a_1 a_2 \ldots a_N
Output
Print the resulting value of X - Y, assuming that the two players play optimally.
Sample Input 1
4 10 80 90 30
Sample Output 1
10
The game proceeds as follows when the two players play optimally (the element being removed is written bold):
- Taro: (10, 80, 90, 30) → (10, 80, 90)
- Jiro: (10, 80, 90) → (10, 80)
- Taro: (10, 80) → (10)
- Jiro: (10) → ()
Here, X = 30 + 80 = 110 and Y = 90 + 10 = 100.
Sample Input 2
3 10 100 10
Sample Output 2
-80
The game proceeds, for example, as follows when the two players play optimally:
- Taro: (10, 100, 10) → (100, 10)
- Jiro: (100, 10) → (10)
- Taro: (10) → ()
Here, X = 10 + 10 = 20 and Y = 100.
Sample Input 3
1 10
Sample Output 3
10
Sample Input 4
10 1000000000 1 1000000000 1 1000000000 1 1000000000 1 1000000000 1
Sample Output 4
4999999995
The answer may not fit into a 32-bit integer type.
Sample Input 5
6 4 2 9 7 1 5
Sample Output 5
2
The game proceeds, for example, as follows when the two players play optimally:
- Taro: (4, 2, 9, 7, 1, 5) → (4, 2, 9, 7, 1)
- Jiro: (4, 2, 9, 7, 1) → (2, 9, 7, 1)
- Taro: (2, 9, 7, 1) → (2, 9, 7)
- Jiro: (2, 9, 7) → (2, 9)
- Taro: (2, 9) → (2)
- Jiro: (2) → ()
Here, X = 5 + 1 + 9 = 15 and Y = 4 + 7 + 2 = 13.
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 450 点
問題文
1 から N までの番号が付けられた N 個の商品がベルトコンベア上を流れています。 ベルトコンベアには印字機が取り付けられており、商品 i は今から T_i [μs] 後に印字機の範囲に入り、その D_i [μs] 後に印字機の範囲から出ます。
キーエンスの印字機は、印字機の範囲内にある商品 1 つに一瞬で印字することができます(特に、商品が印字機の範囲に入る瞬間や範囲から出る瞬間に印字することも可能です)。 ただし、1 度印字すると、次に印字するまでに 1 [μs] のチャージ時間が必要です。 印字機が印字をする商品とタイミングをうまく選んだとき、最大で何個の商品に印字することができますか?
制約
- 1\leq N \leq 2\times 10^5
- 1\leq T_i,D_i \leq 10^{18}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N T_1 D_1 T_2 D_2 \vdots T_N D_N
出力
印字機が印字することのできる商品の数の最大値を出力せよ。
入力例 1
5 1 1 1 1 2 1 1 2 1 4
出力例 1
4
以下、今から t [μs] 後のことを単に時刻 t とよびます。
例えば、次のようにして 4 個の商品に印字することができます。
- 時刻 1 : 商品 1,2,4,5 が印字機の範囲に入る。商品 4 に印字する。
- 時刻 2 : 商品 3 が印字機の範囲に入り、商品 1,2 が印字機の範囲から出る。商品 1 に印字する。
- 時刻 3 : 商品 3,4 が印字機の範囲から出る。商品 3 に印字する。
- 時刻 4.5 : 商品 5 に印字する。
- 時刻 5 : 商品 5 が印字機の範囲から出る。
5 個の商品すべてに印字することはできないため、答えは 4 です。
入力例 2
2 1 1 1000000000000000000 1000000000000000000
出力例 2
2
入力例 3
10 4 1 1 2 1 4 3 2 5 1 5 1 4 1 2 1 4 1 2 4
出力例 3
6
Score : 450 points
Problem Statement
There are N products labeled 1 to N flowing on a conveyor belt. A Keyence printer is attached to the conveyor belt, and product i enters the range of the printer T_i microseconds from now and leaves it D_i microseconds later.
The Keyence printer can instantly print on one product within the range of the printer (in particular, it is possible to print at the moment the product enters or leaves the range of the printer). However, after printing once, it requires a charge time of 1 microseconds before it can print again. What is the maximum number of products the printer can print on when the product and timing for the printer to print are chosen optimally?
Constraints
- 1\leq N \leq 2\times 10^5
- 1\leq T_i,D_i \leq 10^{18}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N T_1 D_1 T_2 D_2 \vdots T_N D_N
Output
Print the maximum number of products the printer can print on.
Sample Input 1
5 1 1 1 1 2 1 1 2 1 4
Sample Output 1
4
Below, we will simply call the moment t microseconds from now time t.
For example, you can print on four products as follows:
- Time 1 : Products 1,2,4,5 enter the range of the printer. Print on product 4.
- Time 2 : Product 3 enters the range of the printer, and products 1,2 leave the range of the printer. Print on product 1.
- Time 3 : Products 3,4 leave the range of the printer. Print on product 3.
- Time 4.5 : Print on product 5.
- Time 5 : Product 5 leaves the range of the printer.
It is impossible to print on all five products, so the answer is 4.
Sample Input 2
2 1 1 1000000000000000000 1000000000000000000
Sample Output 2
2
Sample Input 3
10 4 1 1 2 1 4 3 2 5 1 5 1 4 1 2 1 4 1 2 4
Sample Output 3
6
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 475 点
問題文
頂点に 1 から N の番号が、辺に 1 から M の番号がついた N 頂点 M 辺の重み付き単純連結無向グラフと正整数 K が与えられます。
辺 i\ (1\leq i\leq M) は頂点 u _ i と頂点 v _ i を結んでおり、重みは w _ i です。
このグラフの全域木 T に対して、T のコストを T に含まれる辺の重みの総和を K で割ったあまりで定めます。 このグラフの全域木のコストの最小値を求めてください。
制約
- 2\leq N\leq8
- N-1\leq M\leq\dfrac{N(N-1)}2
- 1\leq K\leq10^{15}
- 1\leq u _ i\lt v _ i\leq N\ (1\leq i\leq M)
- 0\leq w _ i\lt K\ (1\leq i\leq M)
- 与えられるグラフは単純かつ連結
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M K u _ 1 v _ 1 w _ 1 u _ 2 v _ 2 w _ 2 \vdots u _ M v _ M w _ M
出力
答えを出力せよ。
入力例 1
5 6 328 1 2 99 1 3 102 2 3 86 2 4 94 2 5 95 3 4 81
出力例 1
33
与えられるグラフは次のようになります。

辺 1,3,5,6 の 4 本を含む全域木のコストは (99+86+81+95)\bmod{328}=361\bmod{328}=33 となります。 このグラフの全域木のコストはすべて 33 以上であるため、33 を出力してください。
入力例 2
6 5 998244353 1 2 337361568 1 6 450343304 2 3 61477244 2 5 745383438 4 5 727360840
出力例 2
325437688
このグラフのただ一つの全域木のコスト 325437688 を出力してください。
入力例 3
8 28 936294041850197 1 2 473294720906780 1 3 743030800139244 1 4 709363019414774 1 5 383643612490312 1 6 557102781022861 1 7 623179288538138 1 8 739618599410809 2 3 857687812294404 2 4 893923168139714 2 5 581822471860662 2 6 740549363586558 2 7 307226438833222 2 8 447399029952998 3 4 636318083622768 3 5 44548707643622 3 6 307262781240755 3 7 12070267388230 3 8 700247263184082 4 5 560567890325333 4 6 704726113717147 4 7 588263818615687 4 8 549007536393172 5 6 779230871080408 5 7 825982583786498 5 8 713928998174272 6 7 751331074538826 6 8 449873635430228 7 8 11298381761479
出力例 3
11360716373
入力や答えが 32\operatorname{bit} 整数に収まらない場合があることに注意してください。
Score : 475 points
Problem Statement
You are given a weighted simple connected undirected graph with N vertices and M edges, where vertices are numbered 1 to N, and edges are numbered 1 to M. Additionally, a positive integer K is given.
Edge i\ (1\leq i\leq M) connects vertices u_i and v_i and has a weight of w_i.
For a spanning tree T of this graph, the cost of T is defined as the sum, modulo K, of the weights of the edges in T. Find the minimum cost of a spanning tree of this graph.
Constraints
- 2\leq N\leq8
- N-1\leq M\leq\dfrac{N(N-1)}2
- 1\leq K\leq10^{15}
- 1\leq u_i\lt v_i\leq N\ (1\leq i\leq M)
- 0\leq w_i\lt K\ (1\leq i\leq M)
- The given graph is simple and connected.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M K u_1 v_1 w_1 u_2 v_2 w_2 \vdots u_M v_M w_M
Output
Print the answer.
Sample Input 1
5 6 328 1 2 99 1 3 102 2 3 86 2 4 94 2 5 95 3 4 81
Sample Output 1
33
The given graph is shown below:

The cost of the spanning tree containing edges 1,3,5,6 is (99+86+81+95)\bmod{328}=361\bmod{328}=33. The cost of every spanning tree of this graph is at least 33, so print 33.
Sample Input 2
6 5 998244353 1 2 337361568 1 6 450343304 2 3 61477244 2 5 745383438 4 5 727360840
Sample Output 2
325437688
Print the cost of the only spanning tree of this graph, which is 325437688.
Sample Input 3
8 28 936294041850197 1 2 473294720906780 1 3 743030800139244 1 4 709363019414774 1 5 383643612490312 1 6 557102781022861 1 7 623179288538138 1 8 739618599410809 2 3 857687812294404 2 4 893923168139714 2 5 581822471860662 2 6 740549363586558 2 7 307226438833222 2 8 447399029952998 3 4 636318083622768 3 5 44548707643622 3 6 307262781240755 3 7 12070267388230 3 8 700247263184082 4 5 560567890325333 4 6 704726113717147 4 7 588263818615687 4 8 549007536393172 5 6 779230871080408 5 7 825982583786498 5 8 713928998174272 6 7 751331074538826 6 8 449873635430228 7 8 11298381761479
Sample Output 3
11360716373
Note that the input and the answer may not fit into a 32\operatorname{bit} integer.
実行時間制限: 3 sec / メモリ制限: 1024 MiB
ストーリー
AtCoder社は、ロゴ入りの限定グッズをいくつか販売している。 このたび、それらの限定グッズをまとめて値引きした「スペシャルセット」の販売を開始することになった。 高橋くんは、ベルトコンベアで順番に運ばれてくるグッズをダンボール箱に梱包し、配送業者に渡す作業を担当する予定である。 そのため、販売開始に備えて梱包の練習を行うことにした。
配送料はダンボール箱の横幅と縦幅の合計に比例するため、できるだけ小さな箱に詰める必要がある。 各グッズは長方形であり、手元に計測器具がないため、高橋くんは横幅と縦幅を目分量で測り、最適化が得意なあなたに電話で相談することにした。
あなたが電話越しにグッズの配置方法を指示すると、その指示に従って高橋くんは商品を配置する。 そして、その配置において必要となるダンボール箱の横幅と縦幅を再び目分量で計測し、結果をあなたに伝える。 あなたはその情報を元に新しい配置方法を指示する。
このやりとりを繰り返し、すべてのグッズをできるだけ小さなダンボール箱に収める配置方法を求めて欲しい。
問題文
N 個の長方形が与えられる。 i 番目の長方形の大きさは、横幅 w_i と縦幅 h_i である。 入力として、それぞれの値に計測誤差が乗った観測値 w'_i=\mathrm{normal}(w_i, \sigma) と h'_i=\mathrm{normal}(h_i, \sigma) が与えられる。 ここで、\mathrm{normal}(\mu, \sigma) は次の手順で値を生成する関数である。
- 平均 \mu、標準偏差 \sigma の正規分布からランダムに値を生成する。
- 生成した値を四捨五入し、整数に変換する。
- 値が 1 未満の場合は 1 とし、10^9 を超える場合は 10^9 とする。
これらの長方形を、平面上で互いに重ならないように番号順に配置する。 長方形は必要に応じて 90^\circ 回転させ、横幅と縦幅を入れ替えることができる。
右方向に x 軸を、下方向に y 軸を取る。 長方形は x \geq 0 かつ y \geq 0 の領域に配置することができる。 配置方法は以下のような列 (p_0, r_0, d_0, b_0), (p_1, r_1, d_1, b_1), \dots として指定する。
- p_i は i 番目に配置する長方形の番号 (0 \leq p_i \leq N-1) を表す。一部の長方形だけを配置することもできるが、番号は昇順に並んでいなければならず、すべての i < j に対して p_i < p_j を満たす必要がある。
- r_i は長方形を 90^\circ 回転させて配置するかどうかを表す。r_i = 0 の場合、長方形は回転させず、r_i = 1 の場合、回転させる。
- d_i は長方形を配置する方向を表す。d_i が
Uの場合、長方形を下から上へ動かし、既に配置した他の長方形の下端または y = 0 の線に接触したところで停止して配置する。d_i がLの場合、長方形を右から左へ動かし、既に配置した他の長方形の右端または x = 0 の線に接触したところで停止して配置する。 - b_i は長方形を配置する際の基準となる長方形の番号を表す。b_i は -1 または既に配置した長方形の番号である必要がある。
- 下から上に配置する場合 (
U)、b_i は新しい長方形の左端をどの長方形の右端と揃えるかを表す。b_i = -1 の場合、左端が x = 0 になるように配置する。 - 右から左に配置する場合 (
L)、b_i は新しい長方形の上端をどの長方形の下端と揃えるかを表す。b_i = -1 の場合、上端が y = 0 になるように配置する。
- 下から上に配置する場合 (
操作の例
以下の例では、3番の長方形を回転させず、各(d,b)の組に対して配置した結果を図示している。
| 操作(d,b) | 操作前 | (U,-1) | (U,0) | (U,1) | (U,2) |
| 結果 |  |
 |
 |
 |
 |
| 操作(d,b) | 操作前 | (L,-1) | (L,0) | (L,1) | (L,2) |
| 結果 |  |
 |
 |
 |
 |
以下の操作を T 回繰り返す。
- 長方形の配置方法を指定する。前回の配置の続きからではなく、何も置かれていない状態から再度配置をすることに注意。
- 配置後の横幅(長方形が存在する x 座標の最大値)を W、縦幅(長方形が存在する y 座標の最大値)を H とする。このとき、W' = \mathrm{normal}(W, \sigma) と H' = \mathrm{normal}(H, \sigma) の値が計測結果として得られる。
得点
t 回目の配置における横幅を W_t、縦幅を H_t、使用しなかった長方形の集合を U_t とする。このとき、t 回目のスコア s_t を次のように定義する。
\[ s_t = W_t + H_t + \sum_{i\in U_t}(w_i+h_i) \]
このとき、\min_t s_t の値が絶対スコアとして得られる。 絶対スコアは小さければ小さいほど良い。
各テストケース毎に、\mathrm{round}(10^9\times \frac{全参加者中の最小絶対スコア}{自身の絶対スコア}) の相対評価スコアが得られ、その和が提出の得点となる。
最終順位はコンテスト終了後に実施されるより多くの入力に対するシステムテストにおける得点で決定される。 暫定テスト、システムテストともに、一部のテストケースで不正な出力や制限時間超過をした場合、そのテストケースの相対評価スコアは0点となり、そのテストケースにおいては「全参加者中の最小絶対スコア」の計算から除外される。 システムテストは CE 以外の結果を得た一番最後の提出に対してのみ行われるため、最終的に提出する解答を間違えないよう注意せよ。
テストケース数
- 暫定テスト: 50個
- システムテスト: 3000個、コンテスト終了後に seeds.txt (sha256=1e93374aa02130a1167c2893f1904b4234a3b517d1e7b9d25022a9125ff3777d) を公開
相対評価システムについて
暫定テスト、システムテストともに、CE 以外の結果を得た一番最後の提出のみが順位表に反映される。 相対評価スコアの計算に用いられる各テストケース毎の全参加者中の最小絶対スコアの算出においても、順位表に反映されている最終提出のみが用いられる。
順位表に表示されているスコアは相対評価スコアであり、新規提出があるたびに、相対評価スコアが再計算される。 一方、提出一覧から確認出来る各提出のスコアは各テストケース毎の絶対スコアをそのまま足し合わせたものであり、相対評価スコアは表示されない。 最新以外の提出の、現在の順位表における相対評価スコアを知るためには、再提出が必要である。 不正な出力や制限時間超過をした場合、提出一覧から確認出来るスコアは0となるが、順位表には正解したテストケースに対する相対スコアの和が表示されている。
実行時間について
実行時間には多少のブレが生じます。 また、システムテストでは同時に大量の実行を行うため、暫定テストに比べて数%程度実行時間が伸びる現象が確認されています。 そのため、実行時間制限ギリギリの提出がシステムテストでTLEとなる可能性があります。 プログラム内で時間を計測して処理を打ち切るか、実行時間に余裕を持たせるようお願いします。
入出力
まず初めに、長方形の個数 N、操作ターン数 T、計測に発生する誤差の標準偏差 \sigma、各長方形の大きさの計測値 w'_i, h'_i が、以下の形式で標準入力から与えられる。
N T \sigma
w'_0 h'_0
\vdots
w'_{N-1} h'_{N-1}
- 長方形の個数 N は 30\leq N\leq 100 を満たす。
- 操作回数 T は N/2\leq T\leq 4N を満たす。
- 計測時に発生する誤差の標準偏差 \sigma は 1000\leq\sigma\leq 10000 を満たす整数値である。
- 横幅と縦幅の計測値 w'_i, h'_i は 1 以上 10^9 以下の整数値である。
上記の情報を読み込んだ後、以下の処理を T 回繰り返す。
長方形の配置方法を表す列を (p_0, r_0, d_0, b_0), (p_1, r_1, d_1, b_1), \dots, (p_{n-1}, r_{n-1}, d_{n-1}, b_{n-1}) とする。 ここで、n は配置する長方形の個数を表し、n < N であっても良い。 この列を以下の形式で標準出力に出力せよ。
n
p_0 r_0 d_0 b_0
\vdots
p_{n-1} r_{n-1} d_{n-1} b_{n-1}
出力後に、配置の横幅と縦幅の計測値を表す整数 W' と H' が、以下の形式で標準入力から与えられる。
W' H'
出力の後には改行をし、更に標準出力を flush しなければならない。 そうしない場合、TLEとなる可能性がある。
解答プログラムは、# から始まるコメント行を出力に含めても良い。 Web版ビジュアライザを使用すると、コメント行を対応するタイミングで表示出来るため、デバッグや考察等に役立てることが出来る。 ジャッジプログラムはコメント行を全て無視するため、コメント行を出力するプログラムをそのまま提出可能である。
例
| t | Output | Input |
|---|---|---|
| 事前情報 | 4 3 1000 77685 46130 32459 75368 54192 88183 60740 42948 |
|
| 1 | 2 0 0 U -1 1 1 U 0 |
153220 47195 |
| 2 | 4 0 0 U -1 1 1 L -1 2 1 L 1 3 0 U -1 |
167543 86611 |
| 3 | 4 0 0 U -1 1 0 L -1 2 0 U -1 3 0 U 2 |
113031 134437 |
サンプルプログラム
import random
def query(prdb):
print(len(prdb))
for p, r, d, b in prdb:
print(p, r, d, b)
W, H = map(int, input().split())
return W, H
N, T, sigma = map(int, input().split())
wh = [tuple(map(int, input().split())) for _ in range(N)]
rng = random.Random(1234)
for _ in range(T):
prdb = []
for i in range(N):
prdb.append((
i,
rng.randint(0, 1),
['U', 'L'][rng.randint(0, 1)],
rng.randint(-1, i - 1),
))
query(prdb)
入力生成方法
- \mathrm{rand}(L,U): L 以上 U 以下の整数値を一様ランダムに生成する。
- \mathrm{rand\_double}(L,U): L 以上 U 以下の実数値を一様ランダムに生成する。
N, T, \sigma の生成
- N=\mathrm{rand}(30,100)
- T=\mathrm{round}(N\times 2^{\mathrm{rand\_double}(-1,2)})
- \sigma=\mathrm{rand}(1000,10000)
w, h の生成
U=10^5 とし、L=\mathrm{rand}(U/10,U/2) を生成する。 各 i に対し、w_i=\mathrm{rand}(L,U), h_i=\mathrm{rand}(L,U) により生成される。
ツール(入力ジェネレータ・ローカルテスタ・ビジュアライザ)
- Web版: ローカル版より高性能でアニメーション表示が可能です。
- ローカル版: 使用するにはRust言語のコンパイル環境をご用意下さい。
- Windows用のコンパイル済みバイナリ: Rust言語の環境構築が面倒な方は代わりにこちらをご利用下さい。
コンテスト期間中に、ビジュアライズ結果の共有や、解法・考察に関する言及は禁止されています。ご注意下さい。
ツールで用いられる入力ファイルの仕様
ローカルテスタに与える入力ファイルは解答プログラムに与えられる事前情報の末尾に以下の形式の情報が追加されている。
w_0 h_0
\vdots
w_{N-1} h_{N-1}
dW_0 dH_0
\vdots
dW_{T-1} dH_{T-1}
- w_i, h_i は i 番目の長方形の真の横幅と縦幅である。
- dW_t, dH_t は t ターン目の計測結果に加算される計測誤差である。
Story
AtCoder sells several limited-edition goods featuring its logo. They have now decided to launch a "Special Set," which bundles these limited-edition goods at a discounted price. Takahashi is assigned to pack the goods, which are delivered one by one on a conveyor belt, into a single cardboard box and hand it over to a delivery service. To prepare for the launch, he has decided to practice packing.
Since the shipping cost is proportional to the sum of the width and height of the cardboard box, it is necessary to make an effort to pack the goods into as small a box as possible. Each good is rectangular, but Takahashi does not have measuring tools, so he estimates the width and height by eye and consults you, an expert in optimization, over the phone.
When you instruct Takahashi on how to arrange the goods over the phone, he follows your instructions and arranges the items accordingly. He then estimates by eye the width and height of the cardboard box required for that arrangement and reports the results back to you. Based on that information, you provide new instructions for the arrangement.
Repeat this process to find an arrangement that packs all the goods into as small a cardboard box as possible.
Problem Statement
You are given N rectangles. The i-th rectangle has width w_i and height h_i. For each rectangle, observed values w'_i=\mathrm{normal}(w_i, \sigma) and h'_i=\mathrm{normal}(h_i, \sigma) are provided as input, which include measurement errors. Here, \mathrm{normal}(\mu, \sigma) is a function that generates a value through the following steps:
- Generate a random value from a normal distribution with mean \mu and standard deviation \sigma.
- Round the generated value to the nearest integer.
- If the resulting value is less than 1, it is set to 1, and if it exceeds 10^9, it is set to 10^9.
Place these rectangles on a plane in the order of their indices such that they do not overlap. Each rectangle can be rotated 90^\circ, swapping its width and height if necessary.
The positive x-axis extends to the right, and the positive y-axis extends downward. Rectangles can be placed in the region where x \geq 0 and y \geq 0. You are required to specify the placement method as a sequence (p_0, r_0, d_0, b_0), (p_1, r_1, d_1, b_1), \dots, such that:
- p_i represents the index of the rectangle to be placed at the i-th step (0 \leq p_i \leq N-1). You can try placing only some of the rectangles, but the indices must be in ascending order; in other words, for all i < j, p_i < p_j must hold.
- r_i indicates whether the rectangle should be rotated by 90^\circ. If r_i = 0, the rectangle is not rotated; if r_i = 1, the rectangle is rotated.
- d_i specifies the direction in which the rectangle is placed.
- If d_i is
U, the rectangle is moved upward until it stops at the bottom edge of another rectangle that has already been placed or at the line y = 0. - If d_i is
L, the rectangle is moved leftward until it stops at the right edge of another rectangle that has already been placed or at the line x = 0.
- If d_i is
- b_i represents the reference rectangle for placement. b_i must be either -1 or the index of a previously placed rectangle.
- When placing the rectangle upward (
U), b_i specifies which rectangle’s right edge should align with the left edge of the new rectangle. If b_i = -1, the left edge of the rectangle aligns with x = 0. - When placing the rectangle leftward (
L), b_i specifies which rectangle’s bottom edge should align with the top edge of the new rectangle. If b_i = -1, the top edge of the rectangle aligns with y = 0.
- When placing the rectangle upward (
Example of Operations
In the following example, the third rectangle is placed without rotation, and the results of placement are illustrated for each pair of (d, b).
| Operation (d,b) | Before | (U,-1) | (U,0) | (U,1) | (U,2) |
| Result |  |
 |
 |
 |
 |
| Operation (d,b) | Before | (L,-1) | (L,0) | (L,1) | (L,2) |
| Result |  |
 |
 |
 |
 |
Repeat the following operations T times:
- Specify how to place the rectangles. Note that placement starts from an empty state, not continuing from the previous placement.
- After placement, let the width (the maximum x-coordinate where rectangles exist) be W, and the height (the maximum y-coordinate where rectangles exist) be H. Then, the measured values W' = \mathrm{normal}(W, \sigma) and H' = \mathrm{normal}(H, \sigma) are obtained as the results of the measurement.
Scoring
Let W_t and H_t be the width and height of the placement at the t-th turn, respectively, and let U_t be the set of rectangles that are not used in this turn. Then, the score s_t for the t-th turn is defined as follows:
\[ s_t = W_t + H_t + \sum_{i\in U_t}(w_i+h_i) \]
Then you obtain an absolute score of \min_t s_t. The lower the absolute score, the better.
For each test case, we compute the relative score \mathrm{round}(10^9\times \frac{\mathrm{MIN}}{\mathrm{YOUR}}), where YOUR is your absolute score and MIN is the lowest absolute score among all competitors obtained on that test case. The score of the submission is the sum of the relative scores.
The final ranking will be determined by the system test with more inputs which will be run after the contest is over. In both the provisional/system test, if your submission produces illegal output or exceeds the time limit for some test cases, only the score for those test cases will be zero, and your submission will be excluded from the MIN calculation for those test cases.
The system test will be performed only for the last submission which received a result other than CE . Be careful not to make a mistake in the final submission.
Number of test cases
- Provisional test: 50
- System test: 3000. We will publish seeds.txt (sha256=1e93374aa02130a1167c2893f1904b4234a3b517d1e7b9d25022a9125ff3777d) after the contest is over.
About relative evaluation system
In both the provisional/system test, the standings will be calculated using only the last submission which received a result other than CE. Only the last submissions are used to calculate the MIN for each test case when calculating the relative scores.
The scores shown in the standings are relative, and whenever a new submission arrives, all relative scores are recalculated. On the other hand, the score for each submission shown on the submissions page is the sum of the absolute score for each test case, and the relative scores are not shown. In order to know the relative score of submission other than the latest one in the current standings, you need to resubmit it. If your submission produces illegal output or exceeds the time limit for some test cases, the score shown on the submissions page will be 0, but the standings show the sum of the relative scores for the test cases that were answered correctly.
About execution time
Execution time may vary slightly from run to run. In addition, since system tests simultaneously perform a large number of executions, it has been observed that execution time increases by several percent compared to provisional tests. For these reasons, submissions that are very close to the time limit may result in TLE in the system test. Please measure the execution time in your program to terminate the process, or have enough margin in the execution time.
Input and Output
First, the number of rectangles N, the number of operation turns T, the standard deviation \sigma of the measurement error, and the measured sizes w'_i and h'_i of each rectangle are given from Standard Input in the following format.
N T \sigma
w'_0 h'_0
\vdots
w'_{N-1} h'_{N-1}
- The number of rectangles N satisfies 30 \leq N \leq 100.
- The number of operations T satisfies N/2 \leq T \leq 4N.
- The standard deviation of the measurement error \sigma is an integer satisfying 1000 \leq \sigma \leq 10000.
- The measured values of the width and height, w'_i and h'_i, are integers between 1 and 10^9 inclusive.
After reading the above information, repeat the following process T times.
Let the sequence representing the rectangle placement method be (p_0, r_0, d_0, b_0), (p_1, r_1, d_1, b_1), \dots, (p_{n-1}, r_{n-1}, d_{n-1}, b_{n-1}). Here, n represents the number of rectangles to place, and n may be less than N. Output this sequence to Standard Output in the following format.
n
p_0 r_0 d_0 b_0
\vdots
p_{n-1} r_{n-1} d_{n-1} b_{n-1}
After the output, the measured values of the width and height, W' and H', are given from Standard Input in the following format.
W' H'
The output must be followed by a new line, and you have to flush Standard Output. Otherwise, the submission might be judged as TLE.
Your program may output comment lines starting with #. The web version of the visualizer displays the comment lines at the corresponding timing, which may be useful for debugging and analysis. Since the judge program ignores all comment lines, you can submit a program that outputs comment lines as is.
Example
| t | Output | Input |
|---|---|---|
| Prior Information | 4 3 1000 77685 46130 32459 75368 54192 88183 60740 42948 |
|
| 1 | 2 0 0 U -1 1 1 U 0 |
153220 47195 |
| 2 | 4 0 0 U -1 1 1 L -1 2 1 L 1 3 0 U -1 |
167543 86611 |
| 3 | 4 0 0 U -1 1 0 L -1 2 0 U -1 3 0 U 2 |
113031 134437 |
Sample Solution
import random
def query(prdb):
print(len(prdb))
for p, r, d, b in prdb:
print(p, r, d, b)
W, H = map(int, input().split())
return W, H
N, T, sigma = map(int, input().split())
wh = [tuple(map(int, input().split())) for _ in range(N)]
rng = random.Random(1234)
for _ in range(T):
prdb = []
for i in range(N):
prdb.append((
i,
rng.randint(0, 1),
['U', 'L'][rng.randint(0, 1)],
rng.randint(-1, i - 1),
))
query(prdb)
Input Generation
- \mathrm{rand}(L,U): Generates an integer uniformly at random between L and U, inclusive.
- \mathrm{rand\_double}(L,U): Generates a real number uniformly at random between L and U, inclusive.
Generation of N, T, and \sigma
- N = \mathrm{rand}(30, 100)
- T = \mathrm{round}(N \times 2^{\mathrm{rand\_double}(-1, 2)})
- \sigma = \mathrm{rand}(1000, 10000)
Generation of w and h
Let U = 10^5, and generate L = \mathrm{rand}(U/10, U/2).
For each i, w_i = \mathrm{rand}(L, U) and h_i = \mathrm{rand}(L, U) are generated.
Tools (Input generator, local tester, and visualizer)
- Web version: This is more powerful than the local version providing animations.
- Local version: You need a compilation environment of Rust language.
- Pre-compiled binary for Windows: If you are not familiar with the Rust language environment, please use this instead.
Please be aware that sharing visualization results or discussing solutions/ideas during the contest is prohibited.
Specification of input files used by the tools
The input file provided to the local tester includes additional information in the following format appended to the end of the prior-information given to the solution program.
w_0 h_0
\vdots
w_{N-1} h_{N-1}
dW_0 dH_0
\vdots
dW_{T-1} dH_{T-1}
- w_i and h_i represent the true width and height of the i-th rectangle.
- dW_t and dH_t are the measurement errors added to the results of the t-th turn.
実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 525 点
問題文
N 頂点 M 辺の無向グラフ G_0 が与えられます。 G_0 の頂点および辺は、それぞれ頂点 1, 頂点 2, \ldots, 頂点 N および辺 1, 辺 2, \ldots, 辺 M と番号づけられており、 辺 i (1\leq i\leq M) は頂点 U_i と頂点 V_i を結んでいます。
高橋君はグラフ G と、駒 1, 駒 2, \ldots, 駒 N と番号づけられた N 個の駒を持っています。
最初、G=G_0 であり、さらに G の頂点 i (1\leq i\leq N) には駒 i が置かれています。
高橋君はこれから Q 回の操作を順に行います。 i 回目 (1\leq i\leq Q) の操作では 1 以上 M 以下の整数 X_i が与えられ、次の操作を行います。
G において駒 U_{X_i} と駒 V_{X_i} が異なる頂点に置かれており、 それらの間に( G 上の)辺 e が存在するならばその辺を縮約したグラフ G' を作成する。 この際、自己ループができた場合は取り除き、多重辺が存在した場合は単純辺に置き換える。
その後、G において辺 e が結んでいた 2 頂点に置かれていた駒はすべて、G' の e の縮約によって新たに生成された頂点に置く。 G 上のその他の頂点に置かれていた駒については、G' の対応する頂点に置く。 最後に、このようにしてできた G' を新たな G とする。
駒 U_{X_i} と駒 V_{X_i} が同じ頂点に置かれていた場合、あるいは置かれている頂点の間が辺で結ばれていなかった場合は何も行わない。
i=1,2,\ldots, Q 回目の操作それぞれについて、i 回目の操作の後の G の辺の数を出力してください。
辺の縮約 とは
頂点 u と頂点 v を結ぶ辺の縮約とは、頂点 u,v を 1 つの頂点にまとめる操作です。 より正確には、G に対して辺の縮約を行なって得られるグラフとは G に対して次の操作を行って得られるものを指します。- G に新たに頂点 w を追加する。
- G 上の u,v 以外の各頂点 x について、u と x を結ぶ辺、あるいは v と x を結ぶ辺の少なくとも一方が存在するとき、かつその時に限り、w と x を結ぶ辺を加える。
- 頂点 u,v を削除し、頂点 u と v を結ぶ辺および頂点 u または v と他の頂点を結ぶ辺をすべて削除する。
制約
- 2\leq N\leq 3\times 10^5
- 1\leq M\leq 3\times 10^5
- 1\leq U_i<V_i\leq N
- i\neq j ならば (U_i,V_i)\neq (U_j,V_j)
- 1\leq Q\leq 3\times 10^5
- 1\leq X_i\leq M
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 U_2 V_2 \vdots U_M V_M Q X_1 X_2 \ldots X_Q
出力
Q 行出力せよ。 i 行目 (1\leq i\leq Q) には、i 回目の操作の後の G の辺の数を出力せよ。
入力例 1
7 7 1 2 1 3 2 3 1 4 1 5 2 5 6 7 5 1 2 3 1 5
出力例 1
4 3 3 3 2
最初、G は下図のようになっています。丸付き数字はその番号の駒を表します。
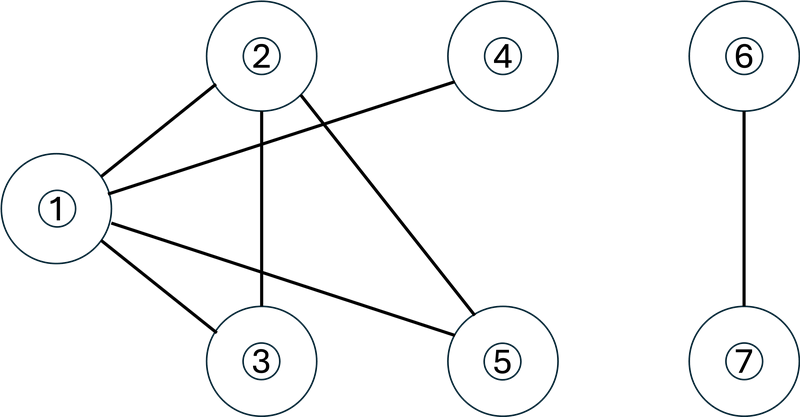
1 回目の操作では、駒 1 と駒 2 が置かれている頂点の間の辺(下図左)の縮約を行います。
操作後、G は下図右のようになり、特に辺の数は 4 です。
自己ループの削除および多重辺の単純辺への置換が行われていることに注意してください。
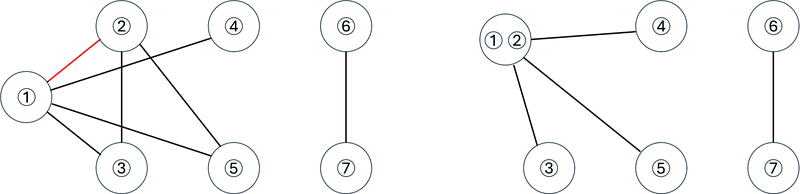
2 回目の操作では、駒 1 と駒 3 が置かれている頂点の間の辺の縮約を行います。
操作後、G は下図左のようになり、辺の数は 3 となります。
3 回目の操作では、駒 2 と駒 3 は同じ頂点に置かれているため、G はそのままであり、辺の数も 3 のままです。
4 回目の操作でも、駒 1 と駒 2 は同じ頂点に置かれているため、G はそのままであり、辺の数も 3 のままです。
5 回目の操作では、駒 1 と駒 5 が置かれている頂点の間の辺の縮約を行います。
操作後、G は下図右のようになり、辺の数は 2 となります。
よって、4,3,3,3,2 をこの順に改行区切りで出力します。
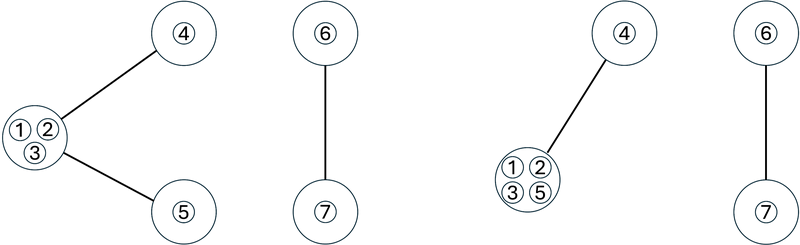
Score : 525 points
Problem Statement
You are given an undirected graph G_0 with N vertices and M edges. The vertices and edges of G_0 are numbered as vertices 1, 2, \ldots, N and edges 1, 2, \ldots, M, respectively, and edge i (1\leq i\leq M) connects vertices U_i and V_i.
Takahashi has a graph G and N pieces numbered as pieces 1, 2, \ldots, N.
Initially, G=G_0, and piece i (1\leq i\leq N) is placed on vertex i of G.
He will now perform Q operations in order. The i-th operation (1\leq i\leq Q) gives an integer X_i between 1 and M, inclusive, and performs the following operation:
In G, if pieces U_{X_i} and V_{X_i} are placed on different vertices and there exists an edge e (on G) between them, create a graph G' by contracting that edge. In this case, if self-loops are created, remove them, and if multi-edges exist, replace them with simple edges.
Then, all pieces that were placed on the two vertices connected by edge e in G are placed on the newly generated vertex by the contraction of e in G'. Pieces that were placed on other vertices in G are placed on the corresponding vertices in G'. Finally, set this resulting G' as the new G.
If pieces U_{X_i} and V_{X_i} are placed on the same vertex, or if the vertices they are placed on are not connected by an edge, do nothing.
For each of the operations i=1,2,\ldots, Q, output the number of edges in G after the i-th operation.
Edge Contraction
Edge contraction of an edge connecting vertices u and v is an operation that merges vertices u,v into one vertex. More precisely, a graph obtained by performing edge contraction on G refers to the result of performing the following operations on G:- Add a new vertex w to G.
- For each vertex x other than u,v in G, if and only if at least one of the edge connecting u and x or the edge connecting v and x exists, add an edge connecting w and x.
- Delete vertices u,v and remove all edges connecting vertices u and v, as well as all edges connecting vertex u or vertex v with other vertices.
Constraints
- 2\leq N\leq 3\times 10^5
- 1\leq M\leq 3\times 10^5
- 1\leq U_i<V_i\leq N
- (U_i,V_i)\neq (U_j,V_j) if i\neq j.
- 1\leq Q\leq 3\times 10^5
- 1\leq X_i\leq M
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M U_1 V_1 U_2 V_2 \vdots U_M V_M Q X_1 X_2 \ldots X_Q
Output
Output Q lines. On the i-th line (1\leq i\leq Q), output the number of edges in G after the i-th operation.
Sample Input 1
7 7 1 2 1 3 2 3 1 4 1 5 2 5 6 7 5 1 2 3 1 5
Sample Output 1
4 3 3 3 2
Initially, G is as shown in the figure below. The circled numbers represent pieces with those numbers.

In the 1st operation, we contract the edge between the vertices where pieces 1 and 2 are placed (left figure below).
After the operation, G becomes as shown in the right figure below, and in particular, the number of edges is 4.
Note that self-loops have been removed and multi-edges have been replaced with simple edges.

In the 2nd operation, we contract the edge between the vertices where pieces 1 and 3 are placed.
After the operation, G becomes as shown in the left figure below, and the number of edges becomes 3.
In the 3rd operation, since pieces 2 and 3 are placed on the same vertex, G remains unchanged, and the number of edges remains 3.
In the 4th operation as well, since pieces 1 and 2 are placed on the same vertex, G remains unchanged, and the number of edges remains 3.
In the 5th operation, we contract the edge between the vertices where pieces 1 and 5 are placed.
After the operation, G becomes as shown in the right figure below, and the number of edges becomes 2.
Thus, output 4,3,3,3,2 in this order, separated by newlines.

実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 475 点
問題文
5 個の 6 面ダイスがあります。どのダイスも各面に書かれた数は A_1,\ldots,A_6 の 6 個であり、各面が出る確率は \frac{1}{6} です。
あなたはこれらのダイスを使って次の手順で 1 人ゲームを行います。
- 5 個のダイスを全て振り、その結果を見て、好きな個数(0 個でもよい)のダイスをキープする。
- キープされていないダイスを全て振り直し、その結果を見て、振り直したダイスのうち好きな個数(0 個でもよい)のダイスを追加でキープする。前のステップでキープしたダイスはキープしたままとなる。
- キープされていないダイスを全て振り直し、その結果を見る。
- 好きな数 X を選ぶ。5 個のダイスのうち X の目が出ているダイスの個数を n として、このゲームの得点は nX 点となる。
ゲームの得点の期待値を最大化するように行動するときの、ゲームの得点の期待値を求めてください。
制約
- A_i は 1 以上 100 以下の整数
入力
入力は以下の形式で標準入力から与えられる。
A_1 A_2 A_3 A_4 A_5 A_6
出力
答えを出力せよ。真の解との相対誤差または絶対誤差が 10^{-5} 以下のとき正解とみなされる。
入力例 1
1 2 3 4 5 6
出力例 1
14.6588633742
例えばゲームは次のように進行します。(最適な行動とは限りません)
- 5 個のダイスを全て振り、それぞれ 3,3,1,5,6 の目が出る。3 の目が出た 2 個のダイスをキープする。
- キープされていない 3 個のダイスを振り、それぞれ 6,6,2 の目が出る。6 の目が出た 2 個のダイスを追加でキープする。
- キープされていない 1 個のダイスを振り、4 の目が出る。
- X として 6 を選ぶ。5 個のダイスの出目はそれぞれ 3,3,6,6,4 なので、6 の目が出ているダイスの個数は 2 であり、このゲームの得点は 12 となる。
このケースでは最適に行動した場合の期待値は \frac{143591196865}{9795520512}=14.6588633742\ldots となります。
入力例 2
1 1 1 1 1 1
出力例 2
5.0000000000
ダイスは同じ値が書かれた面を持つことがあります。
入力例 3
31 41 59 26 53 58
出力例 3
159.8253021021
Score : 475 points
Problem Statement
There are five six-sided dice. Each die has the numbers A_1,\ldots,A_6 written on its faces, and each face appears with probability \frac{1}{6}.
You will play a single-player game using these dice with the following procedure:
- Roll all five dice, observe the results, and keep any number (possibly zero) of dice.
- Re-roll all dice that are not kept, observe the results, and additionally keep any number (possibly zero) of the re-rolled dice. The dice kept in the previous step remain kept.
- Re-roll all dice that are not kept and observe the results.
- Choose any number X. Let n be the number of dice among the five dice that show X. The score of this game is nX points.
Find the expected value of the game score when you act to maximize the expected value of the game score.
Constraints
- A_i is an integer between 1 and 100, inclusive.
Input
The input is given from Standard Input in the following format:
A_1 A_2 A_3 A_4 A_5 A_6
Output
Print the answer. Your answer will be considered correct if the relative or absolute error from the true value is at most 10^{-5}.
Sample Input 1
1 2 3 4 5 6
Sample Output 1
14.6588633742
For example, the game may proceed as follows (not necessarily optimal):
- Roll all five dice and get 3,3,1,5,6. Keep the two dice that show 3.
- Re-roll the three dice that are not kept and get 6,6,2. Additionally keep the two dice that show 6.
- Re-roll the one die that is not kept and get 4.
- Choose X = 6. The dice show 3,3,6,6,4, so the number of dice showing 6 is 2, and the score of this game is 12.
In this case, the expected value when acting optimally is \frac{143591196865}{9795520512}=14.6588633742\ldots.
Sample Input 2
1 1 1 1 1 1
Sample Output 2
5.0000000000
The dice may have faces with the same value written on them.
Sample Input 3
31 41 59 26 53 58
Sample Output 3
159.8253021021