JOIG 2024/2025 本選過去問

A - カードゲーム 4 (Card Game 4)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

カード 1 からカード N までの番号が付けられている N 枚のカードがある．各カードには 1 つの整数が書かれており，カード i (1 \leqq i \leqq N) に書かれた整数は A_i である．

これからあなたは，N 枚のカードから K 枚のカードを選ぶ．このとき，あなたの得点は以下のようになる．

選んだカードに書かれた整数の偶奇がすべて同じ場合，選んだ K 枚のカードに書かれた整数の総和とする．
そうでない場合，0 とする．

カードの情報が与えられたとき，得点としてありうる最大値を求めるプログラムを作成せよ．

制約

1 \leqq N \leqq 100\,000．
1 \leqq K \leqq N．
1 \leqq A_i \leqq 10^9 (1 \leqq i \leqq N)．
入力される値はすべて整数である．

小課題

(30 点) N = K．
(25 点) A_i \leqq 2 (1 \leqq i \leqq N)．
(20 点) A_i は奇数である (1 \leqq i \leqq N)．
(25 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N K
A_1 A_2 \cdots A_N

出力

得点としてありうる最大値を 1 行に出力せよ．

入力例 1

5 5
1 1 1 1 1

出力例 1

カード 1, 2, 3, 4, 5 の 5 枚のカードを選ぶことを考える．このとき，選んだカードに書かれた整数はすべて奇数であるため，この選び方の得点は 1 + 1 + 1 + 1 + 1 = 5 である．

カードの選び方の中で，得点が 6 以上となるものはない．したがって，5 を出力する．

この入力例はすべての小課題の制約を満たす．

入力例 2

6 4
1 2 1 1 2 2

出力例 2

あなたがどのように K 枚のカードを選んでも得点は 0 となる．したがって，0 を出力する．

この入力例は小課題 2, 4 の制約を満たす．

入力例 3

7 3
3 7 9 1 7 5 3

出力例 3

カード 1, 2, 6 の 3 枚のカードを選ぶことを考える．このとき，選んだカードに書かれた整数はすべて奇数であるため，この選び方の得点は 3 + 7 + 5 = 15 である．

カード 2, 3, 5 の 3 枚のカードを選ぶことを考える．このとき，選んだカードに書かれた整数はすべて奇数であるため，この選び方の得点は 7 + 9 + 7 = 23 である．

カードの選び方の中で，得点が 24 以上となるものはない．したがって，23 を出力する．

この入力例は小課題 3, 4 の制約を満たす．

入力例 4

10 3
23 19 21 20 22 18 22 22 24 27

出力例 4

この入力例は小課題 4 の制約を満たす．

B - ポスター 2 (Poster 2)

Time Limit: 5 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 学園の理恵さんは，今年 3 月に実施される文化祭のポスターを作った．このポスターは N 行 N 列のマス目の形をしており，各マスは 1 から K までの番号が付けられた K 種類の色のいずれかで塗られている．具体的には，ポスターの上から i 行目，左から j 列目 (1 \leqq i \leqq N，1 \leqq j \leqq N) は色 A_{i,j} で塗られている．

しかし，このポスターについて生徒間で話し合いを行ったところ，もう少しカラフルにした方が良いのではないかという意見が出た．具体的には，以下で定義されるカラフル度を上げた方が良いのではないかという意見が出た．

連続する 2 行 2 列の正方形領域のうち，3 種類以上の色を含むものの個数．

たとえば，下図左のようなポスターを作った場合，下図右に示す 2 つの長方形領域について 3 種類以上の色を含むため，カラフル度は 2 である．

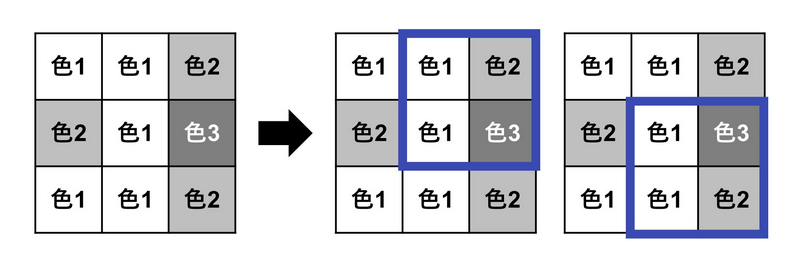
ポスターの提出期限まであと数分しかないので，以下の操作を 0 回または 1 回行うことで，カラフル度を最大化したい．

好きなマスを 1 つ選び，そのマスの色を K 種類の色のいずれかで塗り替える．

理恵さんが最初に作ったポスターの情報が与えられるので，達成できるカラフル度の最大値を求めるプログラムを作成せよ．

制約

2 \leqq N \leqq 270．
3 \leqq K \leqq 10^9．
1 \leqq A_{i,j} \leqq K (1 \leqq i \leqq N，1 \leqq j \leqq N)．
入力される値はすべて整数である．

小課題

(9 点) N = 2，K = 3．
(6 点) A_{i,j} (1 \leqq i \leqq N，1 \leqq j \leqq N) はすべて異なる．
(27 点) N \leqq 10，K \leqq 10．
(26 点) N \leqq 10．
(32 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N K
A_{1,1} A_{1,2} \cdots A_{1,N}
A_{2,1} A_{2,2} \cdots A_{2,N}
\vdots
A_{N,1} A_{N,2} \cdots A_{N,N}

出力

達成できるカラフル度の最大値を 1 行で出力せよ．

入力例 1

2 3
1 2
2 1

出力例 1

以下のように，上から 2 行目，左から 2 列目のマスを色 3 で塗り替えることで，カラフル度 1 を達成することができる．

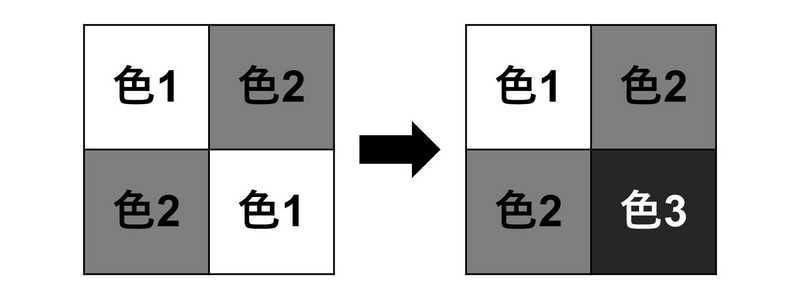
カラフル度 2 以上を達成する方法はないため，1 を出力する．

この入力例は小課題 1, 3, 4, 5 の制約を満たす．

入力例 2

出力例 2

以下のように，上から 2 行目，左から 3 列目のマスを色 4 で塗り替えることで，カラフル度 5 を達成することができる．

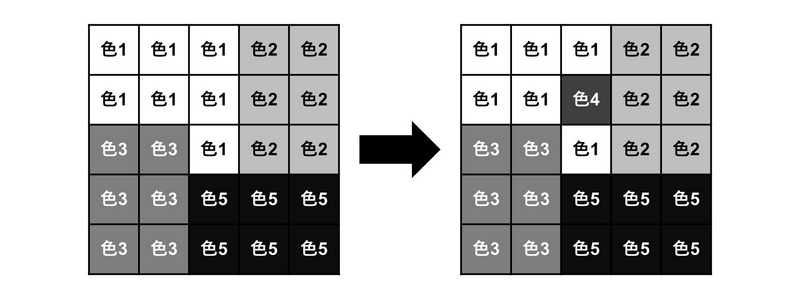
カラフル度 6 以上を達成する方法はないため，5 を出力する．

この入力例は小課題 3, 4, 5 の制約を満たす．

入力例 3

5 1000000000
104289385 946930886 881692778 914636916 257747795
524238335 819885386 849760493 696516649 389641422
225202363 550490028 883368690 302520060 344897765
267513928 565180541 740383427 404089172 503455737
135005211 621595368 394702567 926956430 436465782

出力例 3

この入力例は小課題 2, 4, 5 の制約を満たす．

入力例 4

出力例 4

この入力例は小課題 3, 4, 5 の制約を満たす．

入力例 5

10 11
2 2 1 3 4 3 4 3 3 5
3 2 4 3 4 4 3 3 5 5
3 4 2 2 5 5 5 5 5 5
4 2 2 3 5 3 5 5 5 6
2 2 3 5 5 5 6 6 7 5
4 4 4 5 6 4 6 7 6 6
3 3 5 4 6 6 6 5 6 8
3 3 4 4 6 5 7 7 6 8
4 4 4 6 7 5 5 8 8 7
4 4 6 5 6 6 7 6 6 9

出力例 5

この入力例は小課題 4, 5 の制約を満たす．

C - 修学旅行 (School Trip)

Time Limit: 4 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOIG 高校には 1 から 3^N までの番号がつけられた 3^N 人の生徒がいる．

JOIG 高校の修学旅行の行き先として，アラスカに行く案 A とボリビアに行く案 B があり，どちらにするかを以下のように決定することにした．

長さ 3^N の文字列 S を生徒 i (1 \leqq i \leqq 3^N) が案 A を希望するなら i 文字目は A に，案 B を希望するなら i 文字目は B にすることで定める．
次の操作を N 回行う．
- （操作）：現在の S の長さを X として，長さ \frac{X}{3} の文字列 S' を， S' の j (1\leqq j \leqq \frac{X}{3}) 文字目を S の 3j - 2, 3j - 1, 3j 文字目のうち多く登場する方とすることで定める．S を S' に置き換える．
操作を N 回行った後の S は A あるいは B のいずれかであり，A ならば案 A として，B ならば案 B として決定する．

最初，各生徒がどちらの案を希望するかは長さ 3^N の文字列 T として与えられる．T の i 文字目は，生徒 i が案 A を希望するなら A，案 B を希望するなら B である．この後，Q 回のイベントが起こる．k (1 \leqq k \leqq Q) 回目のイベントでは，生徒 p_k の希望する案を変更する．すなわち，k 回目のイベントの直前での生徒 p_k の希望する案が A なら生徒 p_k の希望する案を B に，そうでないなら A に変更する．

k=1,2,\ldots,Q について，k 回目のイベントが終わった時点での各生徒の希望をもとに修学旅行の行き先を決定した場合にどちらの案が選ばれるかを求めるプログラムを作成せよ．ただし，希望案の変更は一時的なものではなく，その後のイベントに影響することに注意せよ．

制約

1 \leqq N \leqq 12．
1 \leqq Q \leqq 200\,000．
T は長さ 3^N の文字列である．
T の各文字は A または B のいずれかである．
1 \leqq p_k \leqq 3^N (1 \leqq k \leqq Q)．
N, Q, p_k は整数である．

小課題

(8 点) N = 1．
(17 点) Q \leqq 10．
(22 点) p_k \leqq 5 (1 \leqq k \leqq Q)．
(28 点) T の各文字は A である．また，p_k \neq p_l (1\leqq k < l\leqq Q)．
(25 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N Q
T
p_1
p_2
\vdots
p_Q

出力

Q 行にわたって出力せよ．k\,(1 \leqq k \leqq Q) 行目には，k 回目のイベントが終わった時点での各生徒の希望をもとに修学旅行の行き先を決定した場合に案 A が選ばれる場合は A を，案 B が選ばれる場合は B を出力せよ．

入力例 1

2 3
ABABBAABB
3
8
4

出力例 1

B
B
A

1 回目のイベントが終わった時点での各生徒の希望をもとに修学旅行の行き先を決定した場合，案 B が選ばれることは次のようにして分かる．

最初，文字列 S は ABBBBAABB である．
1 回目の操作後，S は BBB となる．
2 回目の操作後，S は B となる．
よって案 B が選ばれる．

2 回目のイベントが終わった時点での各生徒の希望をもとに修学旅行の行き先を決定した場合，案 B が選ばれることは次のようにして分かる．

最初，文字列 S は ABBBBAAAB である．
1 回目の操作後，S は BBA となる．
2 回目の操作後，S は B となる．
よって案 B が選ばれる．

3 回目のイベントが終わった時点での各生徒の希望をもとに修学旅行の行き先を決定した場合，案 A が選ばれることは次のようにして分かる．

最初，文字列 S は ABBABAAAB である．
1 回目の操作後，S は BAA となる．
2 回目の操作後，S は A となる．
よって案 A が選ばれる．

この入力例は小課題 2, 5 の制約を満たす．

入力例 2

2 5
AAAAAAAAA
1
2
7
8
5

出力例 2

A
A
A
B
B

この入力例は小課題 2, 4, 5 の制約を満たす．

入力例 3

出力例 3

A
A
B
B

この入力例は小課題 1, 2, 3, 5 の制約を満たす．

入力例 4

3 6
AABABABBABAABABBBBBBAABABAA
4
1
9
3
8
9

出力例 4

B
B
B
B
B
A

この入力例は小課題 2, 5 の制約を満たす．

D - 最悪の記者 5 (Worst Reporter 5)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

カワウソのウソ太郎は新聞記者であり，近くで開かれる大規模なマラソン大会を取材している．

大会には N 人の選手が参加しており，選手には 1 から N までの番号が付けられている．ウソ太郎はこの大会の取材で，以下の情報をメモに記録した．

大会の開始時点において，N 人の選手は 1 位から N 位までのいずれかの順位であり，それらは互いに相異なっていた．
順位変動はちょうど M 回発生した．i 回目 (1 \leqq i \leqq M) の順位変動では，選手 A_i と選手 B_i の順位が入れ替わった．いずれの順位変動においても，入れ替わる 2 人の順位の差の絶対値は 1 であった．
複数の順位変動が同時に発生することはなかった．

ウソ太郎は，各選手の最終的な順位を表す順位表を新聞に載せたい．順位表は長さ N の数列であり，j 番目 (1 \leqq j \leqq N) の値は最終的に j 位になった選手の番号である．

しかしウソ太郎は，順位表を記録していなかったどころか，各順位変動でどちらが順位を上げた側であったかも記録していなかった．そこでウソ太郎は，メモの情報に矛盾しないような順位表のうち，辞書順で最小のものを選んで報告することにした．

数列 (a_1, a_2, \dots, a_N) が数列 (b_1, b_2, \dots, b_N) よりも辞書順で小さいとは，ある整数 k (1 \leqq k \leqq N) が存在し，以下の条件をともに満たすことをいう．

整数 l (1 \leqq l \leqq k-1) に対し a_l = b_l．
a_k < b_k．

選手の人数 N，およびメモに記録された各順位変動の情報が与えられたとき，メモの情報に矛盾しないような順位表が存在するか判定し，もし存在する場合はそのうち辞書順で最小のものを出力するプログラムを作成せよ．

制約

2 \leqq N \leqq 500\,000．
1 \leqq M \leqq 500\,000．
1 \leqq A_i < B_i \leqq N (1 \leqq i \leqq M)．
入力される値はすべて整数である．

小課題

(13 点) N \leqq 8，M \leqq 8．
(16 点) A_1, A_2, \dots, A_M, B_1, B_2, \dots, B_M は相異なる．
(29 点) N \leqq 1\,000，M \leqq 1\,000．
(23 点) i 回目 (2 \leqq i \leqq M) の順位変動において，A_i と B_i のうち少なくとも片方は A_1, A_2, \dots, A_{i-1}, B_1, B_2, \dots, B_{i-1} の中に現れない値である．
(19 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N M 
A_1 B_1
A_2 B_2
\vdots
A_M B_M

出力

メモの情報に矛盾しないような順位表が存在しない場合，1 行で No と出力せよ．

メモの情報に矛盾しないような順位表が存在する場合，そのうち辞書順で最小のものを以下の形式で N+1 行で出力せよ．

1 行目には Yes を出力せよ．
1+j 行目 (1 \leqq j \leqq N) には，最終的に j 位になった選手の番号を出力せよ．

入力例 1

出力例 1

Yes
2
4
1
5
3

大会の開始時点において，順位ごとの選手の番号は 1 位から順に (1,2,3,5,4) であるとする．

このとき，5 回の順位変動で，順位は以下のように変化する．

1 回目の順位変動で，1 位の選手 1 と 2 位の選手 2 が入れ替わる．この直後において，順位ごとの選手の番号は 1 位から順に (2,1,3,5,4) である．
2 回目の順位変動で，5 位の選手 4 と 4 位の選手 5 が入れ替わる．この直後において，順位ごとの選手の番号は 1 位から順に (2,1,3,4,5) である．
3 回目の順位変動で，3 位の選手 3 と 4 位の選手 4 が入れ替わる．この直後において，順位ごとの選手の番号は 1 位から順に (2,1,4,3,5) である．
4 回目の順位変動で，4 位の選手 3 と 5 位の選手 5 が入れ替わる．この直後において，順位ごとの選手の番号は 1 位から順に (2,1,4,5,3) である．
5 回目の順位変動で，2 位の選手 1 と 3 位の選手 4 が入れ替わる．この直後において，順位ごとの選手の番号は 1 位から順に (2,4,1,5,3) である．

したがって，最終的な順位表は (2,4,1,5,3) となる．

メモの情報に矛盾しないような順位表のうち，(2,4,1,5,3) よりも辞書順で小さいものは存在しない．したがって，(2,4,1,5,3) を出力する．

この入力例は小課題 1, 3, 5 の制約を満たす．

入力例 2

出力例 2

No

メモの情報に矛盾しないような順位表は存在しない．

この入力例は小課題 1, 3, 5 の制約を満たす．

入力例 3

出力例 3

この入力例はすべての小課題の制約を満たす．

入力例 4

出力例 4

この入力例は小課題 1, 3, 4, 5 の制約を満たす．

E - 神経衰弱 2 (Pair Matching 2)

Time Limit: 1 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

2N 枚のカードが机の上に横一列に並んでおり，左から順に 1, 2, \dots, 2N の番号が付けられている．カード i (1 \leqq i \leqq 2N) には整数 A_i が書かれている．各 x = 1, 2, \dots, N について，整数 x が書かれたカードはちょうど 2 枚存在する．

ビーバーのビ太郎は，これらのカードを用いて 神経衰弱 と呼ばれるゲームを行う．ビ太郎は，右手と左手に 1 枚ずつカードを持つことができる．
神経衰弱 は以下の手順で行われる．

i = 1, 2, \dots, 2N の順に以下を行う．
1. ビ太郎は，カード i を拾うか拾わないかを選ぶ．カードを拾おうとする場合，以下の 2. から 5. が順に起こる．カードを拾わない場合，以下の 2. から 5. はスキップする．
2. 整数 A_i が書かれたカードをビ太郎が持っているならば，そのカードと机の上にあるカード i は消滅し，ビ太郎は V_{A_i} の点数を得る．
3. ビ太郎が左手にカードを持っているならば，そのカードを捨てる．
4. ビ太郎が右手にカードを持っているならば，そのカードを左手に移す．
5. カード i が存在する（消滅していない）ならば，ビ太郎は右手でカード i を持つ．

これらの手順で得た点数の合計が最終的なビ太郎のスコアとなる．ビ太郎は，このゲームで得ることのできるスコアの最大値を知りたい．

カードの並びと各整数に割り当てられた点数の情報が与えられたとき，ビ太郎が得ることのできるスコアの最大値を求めるプログラムを作成せよ．

制約

1 \leqq N \leqq 400\,000．
(A_1, A_2, \dots, A_{2N}) は (1, 1, 2, 2, \dots, N, N) の並べ替えである．
1 \leqq V_k \leqq 10^9 (1 \leqq k \leqq N)．
入力される値はすべて整数である．

小課題

(8 点) (A_1, A_2, \dots, A_N) = (1, 2, \dots, N)，N \leqq 5\,000．
(12 点) (A_1, A_2, \dots, A_N) = (1, 2, \dots, N)．
(6 点) N \leqq 9．
(9 点) N \leqq 18．
(16 点) N \leqq 300．
(18 点) N \leqq 3\,000．
(18 点) N \leqq 150\,000，V_k = 1 (1 \leqq k \leqq N)．
(8 点) N \leqq 150\,000．
(5 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N
A_1 A_2 \cdots A_{2N}
V_1 V_2 \cdots V_N

出力

ビ太郎が得ることのできるスコアの最大値を出力せよ．

入力例 1

3
1 2 3 1 2 3
5 2 8

出力例 1

ビ太郎は以下の手順でスコア 13 を得ることができる．

カード 1 を拾おうとする．カード 1 には整数 1 が書かれている．ビ太郎は整数 1 が書かれたカードを持っていないから，カードの消滅は起こらない．ビ太郎は右手にカード 1 を持った状態になる．
カード 2 は拾わずスキップする．
カード 3 を拾おうとする．カード 3 には整数 3 が書かれている．ビ太郎は整数 3 が書かれたカードを持っていないから，カードの消滅は起こらない．ビ太郎は左手にカード 1 を，右手にカード 3 を持った状態になる．
カード 4 を拾おうとする．カード 4 には整数 1 が書かれている．ビ太郎は整数 1 の書かれたカード 1 を持っているから，左手に持ったカード 1 と机の上のカード 4 は消滅し，ビ太郎は V_1 = 5 の点数を得る．その後，ビ太郎は左手にカード 3 を持った状態になる．
カード 5 は拾わずスキップする．
カード 6 を拾おうとする．カード 6 には整数 3 が書かれている．ビ太郎は整数 3 の書かれたカード 3 を持っているから，左手に持ったカード 3 と机の上のカード 6 は消滅し，ビ太郎は V_3 = 8 の点数を得る．その後，ビ太郎はどちらの手にもカードを持っていない状態になる．

ビ太郎は 13 より大きいスコアを得ることはできないため，13 を出力する．

この入力例は小課題 1, 2, 3, 4, 5, 6, 8, 9 の制約を満たす．

入力例 2

4
1 2 1 2 3 4 4 3
39 62 55 21

出力例 2

ビ太郎は，例えばカード 1, 2, 3, 4, 5, 6, 8 を拾おうとすることで，スコア V_1 + V_2 + V_3 = 156 を得ることができる．

ビ太郎は 156 より大きいスコアを得ることはできないため，156 を出力する．

この入力例は小課題 3, 4, 5, 6, 8, 9 の制約を満たす．

入力例 3

10
7 2 5 8 4 10 8 2 7 5 6 3 4 1 10 9 9 1 6 3
185163245 734376902 849123714 97860221 844860642 689054872 471545587 607735137 664633003 831663829

出力例 3

3117416130

この入力例は小課題 4, 5, 6, 8, 9 の制約を満たす．

入力例 4

15
4 3 8 3 10 15 14 1 12 4 13 1 6 7 10 15 2 8 12 2 9 11 11 13 5 9 14 5 6 7
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

出力例 4

この入力例は小課題 4, 5, 6, 7, 8, 9 の制約を満たす．