問題文

時は \mathrm{30XX} 年．科学者・技術者のたゆまぬ努力により，異星間の交流が盛んに行われるようになっていた．ビーバーのビ太郎は異星人に地球の食べ物を紹介するアンバサダーを務めており，今日の午後 1 時に JOI 星へ向けて出発する予定である．

今回 JOI 星人に紹介する食べ物のひとつとして，切り分けたカステラが用意されている．カステラは小麦粉に鶏卵・砂糖・水あめを加え，スポンジ状にふっくらと焼いた菓子である．

カステラは横長の直方体の形をしており，縦方向の切れ目に沿って N 個のピースに分割されている．左から i 番目 (1 \leqq i \leqq N) のピースの長さは整数 A_i である．

つい先ほど，JOI 星人は偶数に嫌悪感を示すということが判明した．そこで対処として，長さが偶数のピースが無くなるまで以下の一連の操作を繰り返すことにした．

1. 長さが偶数のピースのうち最も右にあるものを選ぶ．
2. 選んだピースを縦方向に切って 2 等分する．すなわち，選んだピースの長さを k としたとき，そのピースを位置を変えずに長さ \displaystyle\frac{k}{2} のピース 2 つに分割する．

操作が正しく行われたかチェックするため，ビ太郎は Q 個の質問を準備しておいた．j 番目 (1 \leqq j \leqq Q) の質問は以下の通りである．

• すべての操作が終了したとき，左から X_j 番目にあるピースの長さは何であるか．

カステラと質問の情報が与えられたとき，各質問の答えを求めるプログラムを作成せよ．

制約

• 1 \leqq N \leqq 200\,000．
• 1 \leqq A_i \leqq 1\,000\,000\,000 (1 \leqq i \leqq N)．
• 1 \leqq Q \leqq 200\,000．
• 1 \leqq X_j \leqq 1\,000\,000\,000\,000\,000\ (= 10^{15}) (1 \leqq j \leqq Q)．
• X_{j} \leqq X_{j + 1} (1 \leqq j \leqq Q - 1)．
• すべての操作が終了したとき，カステラは X_Q 個以上のピースに分割されている．

小課題

1. (25 点) A_i \leqq 8 (1 \leqq i \leqq N)．
2. (35 点) N \leqq 1\,000，Q \leqq 1\,000．
3. (40 点) 追加の制約はない．

入力例 1

4
14
9
8
12
6
2
3
5
7
11
13

出力例 1

7
9
1
1
1
3

はじめ，カステラの各ピースの長さは左から順に 14, 9, 8, 12 である．

一連の操作が終了したとき，カステラは 15 個のピースに分割されており，各ピースの長さは左から順に 7, 7, 9, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3 となる．

この入出力例は小課題 2, 3 の制約を満たす．

入力例 2

13
1
4
1
4
2
1
3
5
6
2
3
7
3
8
2
10
11
13
15
17
18
20

出力例 2

1
1
1
1
5
3
1
3

この入出力例はすべての小課題の制約を満たす．

入力例 3

16
536870912
402653184
536870912
536870912
134217728
536870912
671088640
536870912
536870912
536870912
939524096
805306368
536870912
956301312
536870912
536870912
5
2500000000
3355443201
4294967296
5111111111
6190792704

出力例 3

5
1
7
57
1

この入出力例は小課題 2, 3 の制約を満たす．

JOI 高校一年の 3 学期は，第 1 週から第 M 週までの M 週間にわたって N 科目の授業が行われる．それぞれの科目には 1 から N までの番号が付けられている．また，授業は週 N コマあり，各週の i コマ目 (1 \leqq i \leqq N) には科目 i の授業が行われる．

高校一年生のビ太郎は，N \times M 個のコマそれぞれにおいて，以下のいずれかの行動をとることができる．

• 行動 1：そのコマの授業に出席する．科目 i (1 \leqq i \leqq N) の授業に 1 コマ出席した場合，その科目の理解度が A_i 増加する．
• 行動 2：そのコマの授業に出席せず，科目を自由に 1 つ選んで自習を行う．科目 i (1 \leqq i \leqq N) の自習を 1 コマ行った場合，その科目の理解度が B_i 増加する．

ただし，最初の時点では全科目について理解度が 0 であるものとする．また，放課後は競技プログラミングの練習に費やしたいので，授業時間以外に勉強をしないものとする．

3 学期の授業がすべて終わると，期末試験が行われる．ビ太郎はその試験で赤点を取りたくないので，試験が行われる時点で，理解度が最も小さい科目の理解度をできるだけ大きくしたい．

学期の長さ，科目数と理解度の増加分が与えられたとき，試験が行われる時点での理解度の最小値として考えられる最大の値を求めるプログラムを作成せよ．

制約

• 1 \leqq N \leqq 300\,000．
• 1 \leqq M \leqq 1\,000\,000\,000．
• 1 \leqq A_i \leqq 1\,000\,000\,000 (1 \leqq i \leqq N)．
• 1 \leqq B_i \leqq 1\,000\,000\,000 (1 \leqq i \leqq N)．

小課題

1. (10 点) M = 1．
2. (25 点) N \times M \leqq 300\,000，A_i = B_i (1 \leqq i \leqq N)．
3. (27 点) N \times M \leqq 300\,000．
4. (29 点) A_i = B_i (1 \leqq i \leqq N)．
5. (9 点) 追加の制約はない．

入力例 1

3 3
19 4 5
2 6 2

出力例 1

18

たとえば次のような方法で勉強をすると，試験が行われる時点で，科目 1, 2, 3 の理解度がそれぞれ 19, 18, 19 となる．

• 第 1 週の 1 コマ目は，科目 2 の自習を行う．
• 第 1 週の 2 コマ目は，科目 2 の自習を行う．
• 第 1 週の 3 コマ目は，科目 3 の授業に出席する．
• 第 2 週の 1 コマ目は，科目 1 の授業に出席する．
• 第 2 週の 2 コマ目は，科目 3 の自習を行う．
• 第 2 週の 3 コマ目は，科目 3 の授業に出席する．
• 第 3 週の 1 コマ目は，科目 3 の自習を行う．
• 第 3 週の 2 コマ目は，科目 2 の自習を行う．
• 第 3 週の 3 コマ目は，科目 3 の授業に出席する．

理解度の最小値を 19 以上にする方法は存在しないため，18 を出力する．

この入出力例は小課題 3, 5 の制約を満たす．

入力例 2

2 1
9 7
2 6

出力例 2

7

この入出力例は小課題 1, 3, 5 の制約を満たす．

入力例 3

5 60000
630510219 369411957 874325200 990002527 567203997
438920902 634940661 593780254 315929832 420627496

出力例 3

41397427274960

この入出力例は小課題 3, 5 の制約を満たす．

入力例 4

4 25
1 2 3 4
1 2 3 4

出力例 4

48

この入出力例は小課題 2, 3, 4, 5 の制約を満たす．

JOI 国は N 個の州からなり，それぞれ 1 から N までの番号が付けられている．2022 年，JOI 国では大統領選挙が開催されることになった．この選挙では各州で投票が行われ，勝った候補者がその州に割り当てられている 1 票を獲得する．

さて，大統領選挙に出馬する理恵さんは，演説によって自身への信頼度を上げ，選挙で勝とうと考えた．演説により，具体的には次のことが起こる．

• 州 i (1 \leqq i \leqq N) での合計演説時間が A_i 時間に達すると，その州に割り当てられている 1 票を獲得できる．
• 州 i (1 \leqq i \leqq N) での合計演説時間が B_i 時間に達すると，協力者 1 人を得ることができる．得られた協力者は，それ以降演説を行い，合計演説時間を増やすことができる．
• ただし，州 i からの協力者を得られない場合もあり，その場合は B_i = -1 として情報が与えられる．それ以外の場合は，B_i \geqq A_i であることが保証される．

なお，州 i (1 \leqq i \leqq N) で獲得した協力者が州 i 以外で演説をすることや，1 つの州で同時に 2 人以上が演説をすることも可能である．たとえば，ある州で同時に 2 人が x 時間演説をした場合，この州の合計演説時間は 2x 時間増加する．ただし，演説時間が整数である必要はない．また，州の間を移動する時間は無視できるものとする．

投票日が近いので，理恵さんは目標の K 票をできるだけ早く獲得したい．

州の数と各州の情報が与えられたとき，K 票を集めるまでにかかる時間の最小値を求めるプログラムを作成せよ．

制約

• 1 \leqq N \leqq 500．
• 1 \leqq K \leqq N．
• 1 \leqq A_i \leqq 1\,000 (1 \leqq i \leqq N)．
• A_i \leqq B_i \leqq 1\,000 または B_i = -1 (1 \leqq i \leqq N)．

小課題

1. (5 点) B_i = -1 (1 \leqq i \leqq N)．
2. (5 点) B_i = -1 または B_i = A_i (1 \leqq i \leqq N)．
3. (11 点) N \leqq 7．
4. (12 点) N \leqq 20．
5. (33 点) N \leqq 100．
6. (11 点) K = N．
7. (23 点) 追加の制約はない．

入力例 1

3
3
1 5
2 3
4 5

出力例 1

5.500000000000000

以下のような順序で選挙活動を行うと，5.5 時間ですべての州の票を獲得することができる．

1. 理恵さんが州 2 で 2 時間演説を行い，その州の票を得る．
2. 理恵さんが州 2 でさらに 1 時間演説を行い，その州の協力者を得る．
3. 理恵さんと協力者 1 人が州 3 で 2 時間演説を行い，その州の票を得る．
4. 理恵さんと協力者 1 人が州 1 で 0.5 時間演説を行い，その州の票を得る．

この入力例は小課題 3, 4, 5, 6, 7 の制約を満たす．

入力例 2

7
4
4 -1
11 -1
6 -1
12 -1
36 -1
11 -1
20 -1

出力例 2

32.000000000000000

以下のような順序で選挙活動を行うと，32 時間で 4 票を獲得することができる．

1. 理恵さんが州 1 で 4 時間演説を行い，その州の票を得る．
2. 理恵さんが州 2 で 11 時間演説を行い，その州の票を得る．
3. 理恵さんが州 3 で 6 時間演説を行い，その州の票を得る．
4. 理恵さんが州 6 で 11 時間演説を行い，その州の票を得る．

この入力例は小課題 1, 2, 3, 4, 5, 7 の制約を満たす．

入力例 3

5
3
4 -1
5 -1
6 -1
7 7
8 8

出力例 3

11.500000000000000

以下のような順序で選挙活動を行うと，11.5 時間で 3 票を獲得することができる．

1. 理恵さんが州 4 で 7 時間演説を行い，その州の票と協力者を得る．
2. 理恵さんが州 1 で 4 時間演説を行い，その州の票を得る．同時に，協力者 1 人が州 2 で 4 時間演説を行う．
3. 理恵さんと協力者 1 人が州 2 で 0.5 時間演説を行い，その州の票を得る．

この入力例は小課題 2, 3, 4, 5, 7 の制約を満たす．

入力例 4

7
5
28 36
11 57
20 35
19 27
31 33
25 56
38 51

出力例 4

62.166666666666664

この入力例は小課題 3, 4, 5, 7 の制約を満たす．

入力例 5

20
14
106 277
175 217
170 227
164 245
118 254
139 261
142 270
185 200
162 241
153 239
128 264
103 299
147 248
158 236
160 232
183 205
194 197
135 260
153 234
128 260

出力例 5

644.203571428571422

この入力例は小課題 4, 5, 7 の制約を満たす．

IOI 鉄道は 1 本の鉄道路線を運営している．IOI 鉄道線には一直線上に並んだ N 個の駅があり，1 から N までの番号が付けられている．各 i (1 \leqq i \leqq N - 1) に対して，駅 i と駅 i + 1 の間は線路で結ばれている．

IOI 鉄道線には M 系統の運行系統があり，1 から M までの番号が付けられている．系統 j (1 \leqq j \leqq M) の列車の始発駅は駅 A_j であり，終着駅は駅 B_j である．列車は各駅に停車する．すなわち，系統 j の列車は，A_j < B_j のとき駅 A_j，駅 A_j + 1，\dots，駅 B_j の順に停車し，A_j > B_j のとき駅 A_j，駅 A_j - 1，\dots，駅 B_j の順に停車する．

旅人の JOI くんは，Q 個の旅行計画を考えている．k 番目 (1 \leqq k \leqq Q) の計画は，駅 S_k から出発し，駅 T_k にいくつかの列車を乗り継いで到着するというものである．

しかしながら，JOI くんは長旅で疲れているので，空いている列車に乗車し，着席したい．そのため，JOI くんがある列車に乗車するのは，その列車の始発駅から（始発駅を含めて）K 駅以内の駅からのみとした．すなわち，JOI くんが系統 j の列車に乗車するとき，A_j < B_j であれば駅 A_j，駅 A_j + 1，\dots，駅 \min\{A_j + K - 1, B_j - 1\} から乗車でき，A_j > B_j であれば駅 A_j，駅 A_j - 1，\dots，駅 \max\{A_j - K + 1, B_j + 1\} から乗車できる．JOI くんは，列車に乗車した駅の次の駅からその列車の終着駅までの各駅のうちいずれかの駅で下車する．

JOI くんはこの条件のもと，なるべく乗り継ぎの回数を少なくしたい．

IOI 鉄道線の情報と JOI くんの計画が与えられたとき，それぞれの計画について，JOI くんが計画を達成するために乗車する列車の数の最小値を求めるプログラムを作成せよ．

制約

• 2 \leqq N \leqq 100\,000．
• 1 \leqq K \leqq N - 1．
• 1 \leqq M \leqq 200\,000．
• 1 \leqq A_j \leqq N (1 \leqq j \leqq M)．
• 1 \leqq B_j \leqq N (1 \leqq j \leqq M)．
• A_j \neq B_j (1 \leqq j \leqq M)．
• (A_j, B_j) \neq (A_k, B_k) (1 \leqq j < k \leqq M)．
• 1 \leqq Q \leqq 50\,000．
• 1 \leqq S_k \leqq N (1 \leqq k \leqq Q)．
• 1 \leqq T_k \leqq N (1 \leqq k \leqq Q)．
• S_k \neq T_k (1 \leqq k \leqq Q)．
• (S_k, T_k) \neq (S_l, T_l) (1 \leqq k < l \leqq Q)．

小課題

1. (8 点) N \leqq 300，M \leqq 300，Q \leqq 300．
2. (8 点) N \leqq 2\,000，M \leqq 2\,000，Q \leqq 2\,000．
3. (11 点) Q = 1．
4. (25 点) K = N - 1．
5. (35 点) A_j < B_j (1 \leqq j \leqq M)，S_k < T_k (1\leqq k \leqq Q)．
6. (13 点) 追加の制約はない．

入力例 1

5 2
2
5 1
3 5
3
5 3
3 2
2 1

出力例 1

1
2
-1

1 番目の計画は，駅 5 から出発し，駅 3 に到着するというものである．例えば，駅 5 から系統 1 の列車に乗車し，駅 3 で下車することで計画を達成できる．このとき乗車する列車の数は 1 本である．1 本未満の列車に乗車することで計画を達成することは不可能であるため，1 を 1 行目に出力する．

2 番目の計画は，駅 3 から出発し，駅 2 に到着するというものである．例えば，駅 3 から系統 2 の列車に乗車し，駅 4 で下車し，そして，駅 4 から系統 1 の列車に乗車し，駅 2 で下車することで計画を達成できる．このとき乗車する列車の数は 2 本である．2 本未満の列車に乗車することで計画を達成することは不可能であるため，2 を 2 行目に出力する．駅 3 から系統 1 の列車に乗車することはできないことに注意すること．

3 番目の計画は，駅 2 から出発し，駅 1 に到着するというものである．この計画は達成できないため，-1 を 3 行目に出力する．

この入力例は小課題 1, 2, 6 の制約を満たす．

入力例 2

6 3
2
1 6
5 1
4
5 1
6 3
3 6
2 1

出力例 2

1
-1
1
2

この入力例は小課題 1, 2, 6 の制約を満たす．

入力例 3

6 5
4
3 1
2 4
5 3
4 6
5
1 5
3 2
2 6
6 3
5 4

出力例 3

-1
1
2
-1
1

この入力例は小課題 1, 2, 4, 6 の制約を満たす．

入力例 4

12 1
5
1 7
10 12
3 5
8 10
5 9
7
2 11
5 8
3 12
4 6
1 9
9 10
1 4

出力例 4

-1
1
4
-1
2
-1
1   

この入力例は小課題 1, 2, 5, 6 の制約を満たす．

JOI 君は，砂浜で砂の城を作って遊んだ．JOI 君が作った城は，砂浜のある長方形の領域に含まれている．この長方形の領域は縦 H 行，横 W 列に区切られたマス目として表され，縦方向は南北方向に平行であり，横方向は東西方向に平行である．北から i 行目 (1 \leqq i \leqq H)，西から j 列目 (1 \leqq j \leqq W) のマスの高さは A_{i, j} である．ただし，A_{i, j} の値はすべて相異なる．

この砂の城に対し，JOI 君は以下の行動を行った．

1. あるマスを選び，そのマスの上からスタートする．
2. その後，東西南北に隣接するより低いマスの上に移動することを，0 回以上繰り返す．

最終的に JOI 君が訪れたマスの領域を上から見ると，これは 1 つの長方形で表された．

各マスの高さ A_{i, j} の情報が与えられたとき，JOI 君が訪れたマスの長方形領域としてあり得るものが何通りあるかを求めるプログラムを作成せよ．

制約

• H \geqq 1．
• W \geqq 1．
• H \times W \leqq 50\,000．
• 1 \leqq A_{i, j} \leqq 10\,000\,000 (1 \leqq i \leqq H，1 \leqq j \leqq W)．
• A_{i_1, j_1} \neq A_{i_2, j_2} (1 \leqq i_1 \leqq H，1 \leqq j_1 \leqq W，1 \leqq i_2 \leqq H，1 \leqq j_2 \leqq W，(i_1, j_1) \neq (i_2, j_2))．

小課題

1. (9 点) H = 1．
2. (10 点) H \times W \leqq 100．
3. (5 点) H \times W \leqq 1\,500．
4. (56 点) H \times W \leqq 7\,000．
5. (20 点) 追加の制約はない．

入力例 1

1 5
2 4 7 1 5

出力例 1

10

JOI 君が訪れたマスの長方形領域として，以下の 10 通りがあり得るため，10 を出力する．

入力例 2

3 2
18 10
19 12
17 13

出力例 2

15

JOI 君が訪れたマスの長方形領域として，以下の 15 通りがあり得るため，15 を出力する．

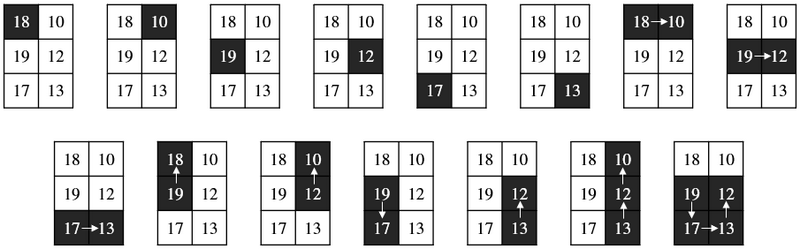
この入力例は小課題 2, 3, 4, 5 の制約を満たす．

入力例 3

3 5
83 47 36 38 40
13 10 26 68 67
15 19 20 70 90

出力例 3

65

例えば，以下の長方形領域が考えられる．それ以外のものも含めると全部で 65 通りあるため，65 を出力する．

この入力例は小課題 2, 3, 4, 5 の制約を満たす．