A - Invest Master

実行時間制限: 2 sec / メモリ制限: 128 MB

長年の研究の末、イクタ君は未来予知能力を手に入れた！　彼がこの研究に費やした時間や金銭は莫大なものであったが、ついに報われる時がやってきたのだ。手始めに金銭を取り戻すため、イクタ君は株式投資を始めることにした。

イクタ君は現在株式は全く保有しておらず、 x 円を所持している。彼が投資対象に定めた株式は n 種類で、それらについて今日から d 日分の株価を予知することに成功した。その結果、驚くべきことに今日から d 日間は日中の株価変動が全くないことが判明した。つまり、今日を1日目としたときの i （1 \leq i \leq d）日目の株式 j （1 \leq j \leq n）の株価 p_i,j 円がわかっている。イクタ君はそれぞれの日に自由に株式を売買できる。すなわち、任意の時点で以下の操作（購入・売却）を任意の順番で任意の回数行える。ただし、各操作の前後での所持金と株式の保有単位数は非負整数でなければならない。

購入 : i 日目に、株式の種類 j （1 \leq j \leq n）を一つ選び、所持金 p_i,j 円を支払い1単位の株式 j を得る。
売却 : i 日目に、株式の種類 j （1 \leq j \leq n）を一つ選び、1単位の株式 j を支払い p_i,j 円を得る。

（彼が研究に没頭する間に証券取引システムは大きな発達を遂げ、取引手数料はかからなくなった。）

イクタ君は大学で情報科学を修めていたが、未来予知研究に明け暮れるすえに大学で学んだことをすべて忘れてしまっていた。そんな彼の代わりに最終日の所持金を最大化するプログラムを書いてあげてほしい。

Input

入力は以下の形式で与えられる。

n d x
p_1,1 ... p_1,n
...
p_d,1 ... p_d,n

n : 株式の種類数
d : 日数
x : 1日目の所持金
p_i,j : i 日目の銘柄jの株価（今日を1日目とする）

Constraints

入力中の各変数は以下の制約を満たす整数である。

1 \leq n \leq 10
1 \leq d \leq 10
1 \leq x, p_i,j \leq 10⁵
最終日の所持金が 10⁵ 以下となることが保証されている。

Output

最適に投資した場合の最終日の所持金を1行に出力せよ。

Sample Input 1

2 2 5
3 2
5 4

Output for the Sample Input 1

例えば、それぞれの株式を1単位ずつ購入します。

Sample Input 2

1 2 5
6
10000

Output for the Sample Input 2

1単位より小さい取引はできません。小口投資家の悲哀です。

Sample Input 3

Output for the Sample Input 3

1日目は1種類目の株式に、2日目は2種類目の株式に投資します。

Sample Input 4

Output for the Sample Input 4

景気が悪い時もあります。

B - Minus One

実行時間制限: 2 sec / メモリ制限: 128 MB

イクタ君は、無向グラフについて異常なほどの思い入れを持っている。イクタ君は、無向グラフ G とその 2 点 s,tの組(G,s,t)のうち、その「うつくしさ」が大きいものが好きである。組(G,s,t)の「うつくしさ」とは、辺 e = \{u, v\} (u と v は G の異なる 2 点) で、Gにおけるsからtへの最短路の長さが、Gにeをつけくわえた無向グラフにおけるsからtへの最短路の長さより 1 だけ大きいものの個数である。

あなたの仕事は、組(G,s,t)が与えられたとき、その「うつくしさ」を求めるプログラムを書くことである。

Input

入力は以下の形式で与えられる。

N M s t
x₁ y₁
...
x_i y_i
...
x_M y_M

最初に無向グラフの頂点数、辺数、2つの頂点を表す整数N,M,s,tが入力される。 2行目からM+1行目までは辺によって結ばれている2つの頂点が入力される。 (ただし、G の頂点集合を\{1,..., N\}とする。)

Constraints

入力中の各変数は以下の制約を満たす。

2\leq N \leq 100,000
1\leq M \leq 300,000
1\leq s,t,x_i,y_i \leq N
s と t とは異なる
s から t に辿り着けることは保証されている

Output

与えられたグラフをGとしたとき、組(G,s,t)の「うつくしさ」を1行で出力せよ。

Sample Input 1

3 2 1 3
1 2
2 3

Output for the Sample Input 1

頂点1から頂点3に辺を張ると、2点間の最短距離が 1 短くなる。

Sample Input 2

Output for the Sample Input 2

Sample Input 3

Output for the Sample Input 3

頂点1と頂点4には既に辺が張られているので、これ以上距離を縮めることはできない。

Sample Input 4

Output for the Sample Input 4

C - Wave Attack

実行時間制限: 2 sec / メモリ制限: 128 MB

勇猛果敢なイクタ君はついに悪名高きビッグブリッジ伯爵を追い詰めた！　今やビッグブリッジ伯爵は幅 w メートル、奥行き h メートルの長方形の部屋に閉じ込められており、最期を待つばかりとなっている。

部屋のある角を選び、幅方向を x 軸、奥行き方向を y 軸に、それぞれ部屋の内部が正の方向になるように座標系をとると、ビッグブリッジ伯爵は点 (p, q) にいる。点 (x, y) にイクタ君の最終兵器である衝撃波発射装置があり、ここから秒速 v メートルの衝撃波を全方向に出す。この衝撃波は t 秒間有効であり、部屋の壁面で反射する。

部屋の外にいるイクタ君はビッグブリッジ伯爵がどれだけ苦しむか知りたがっているので、ビッグブリッジ伯爵に衝撃波が何回当たるかを求めるプログラムを書いてあげよう。このとき、衝撃波が同時に n 方向から敵に当たる場合は n 回当たったとみなし、また衝撃波がちょうど t 秒後に敵に当たる場合も有効であるとする。衝撃波は発射装置自身やビッグブリッジ伯爵などの障害物により消滅せず、衝撃波同士は干渉しない。

Input

入力は以下の形式で与えられる。

w h v t x y p q

それぞれは問題文の説明の通りの正の整数である。

Constraints

v × t ≤ 10⁶
2 ≤ w, h ≤ 10⁸
0 < x, p < w
0 < y, q < h
(x, y) ≠ (p, q)

Output

衝撃波がビッグブリッジ伯爵に当たる回数を1行に出力せよ。

Sample Input 1

10 10 1 10 3 3 7 7

Output for the Sample Input 1

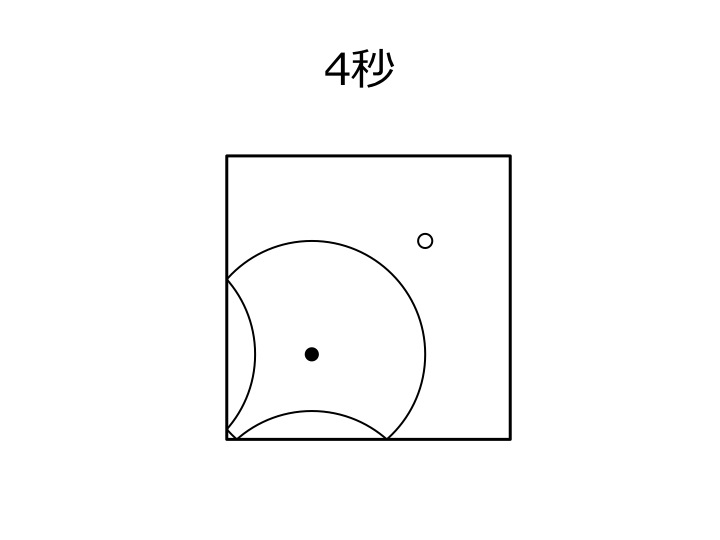
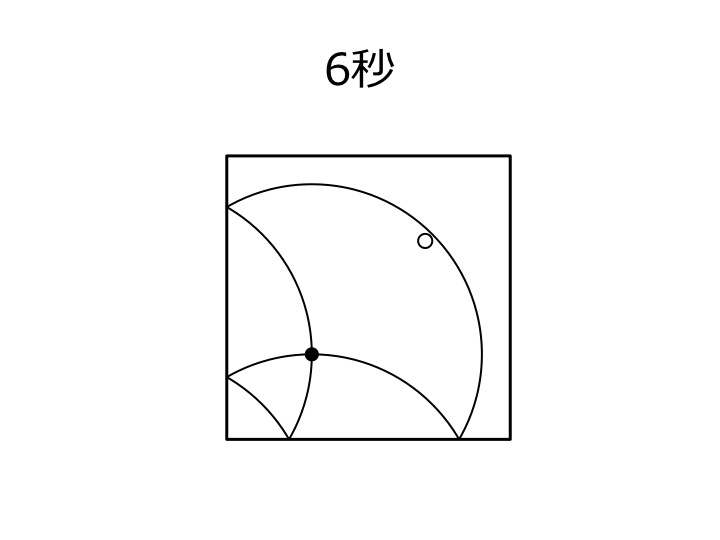
Sample Input 2

10 10 1 11 3 3 7 7

Output for the Sample Input 2

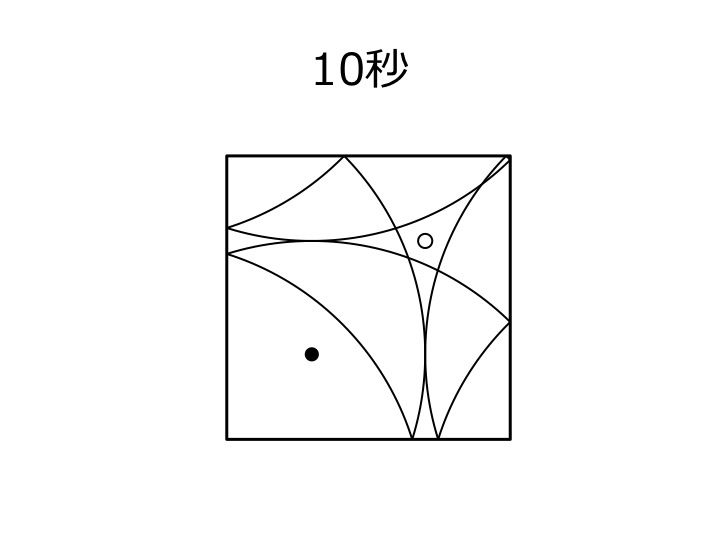
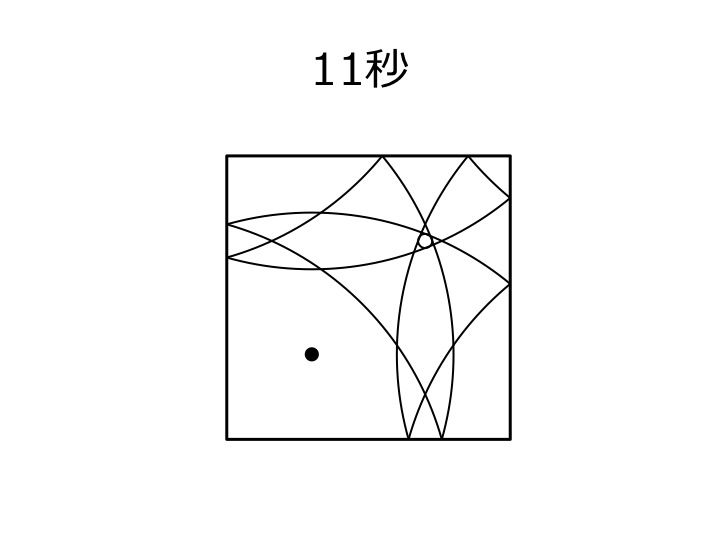
入力例 1, 2 において部屋の大きさと発射装置とビッグブリッジ伯爵の位置が同じであることに注意しながら、それぞれに付随する図（黒い点が発射装置、白い点がビッグブリッジ伯爵を表す）を見よ。

Sample Input 3

2 3 1000 1000 1 1 1 2

Output for the Sample Input 3

523598775681

D - Fast Division

実行時間制限: 2 sec / メモリ制限: 128 MB

イクタ君は速いプログラムが大好きである。最近は、除算のプログラムを高速にしようとしている。しかしなかなか速くならないので、「常識的に考えて典型的」な入力に対してのみ高速にすればよいと考えた。イクタ君が解こうとしている問題は次のようなものである。

与えられた非負整数nに対し、10進法でp(n) - 1桁の正整数11...1をp(n)で割ったあまりを求めよ。ただしp(n)は2^{2^{...²}}（2がn個）より大きい最小の素数を表すとする。p(0) = 2とする。

あなたの仕事は、イクタ君より速くプログラムを完成させることである。

Input

入力は以下の形式で与えられる。

n

問題の入力の非負整数nがあたえられる。

Constraints

入力中の各変数は以下の制約を満たす。

0 \leq n < 1000

Output

問題の解を1行に出力せよ。

Sample Input 1

Output for the Sample Input 1

n=0のとき、p(n) = 2 なので、1 mod 2 = 1 が解となる。

Sample Input 2

Output for the Sample Input 2

n=1のとき、p(n) = 3 なので、11 mod 3 = 2が解となる。

Sample Input 3

Output for the Sample Input 3

E - 順位付け

実行時間制限: 2 sec / メモリ制限: 128 MB

イクタ君の住む町にはN個の塔がある。それぞれの塔には0からN-1までの異なる番号が与えられており、番号iの塔を塔iと呼ぶ。好奇心旺盛なイクタ君はN個の塔の高さに興味を持ち、それらの大小関係を表す表Tを作ることにした。 TはN \times N個の要素を持ち、各要素T_{i, j} (0 \leq i, j \leq N - 1)は次のように定義される。

T_{i, j} = -1⇔ 塔iの高さが塔jの高さより小さい
T_{i, j} = 0 ⇔ 塔iの高さと塔jの高さが等しい
T_{i, j} = 1 ⇔ 塔iの高さが塔jの高さより大きい

イクタ君は表Tを作成するための調査として、2つの塔を選びそれらの高さを比較するということをN-1回繰り返した。

イクタ君の調査に関して以下のことがわかっている。

i回目の比較(1 \leq i \leq \ N - 1)で塔a_i, 塔b_iが選ばれたとすると塔a_iの高さが塔b_iの高さより大きかった。つまりT_{a_i, b_i} = 1, T_{b_i, a_i} = -1であった。
それぞれの塔は自分自身よりも大きな塔とは高々一回しか比較されていない。

残念ながらイクタ君の調査による情報だけで表Tの内容を一意に決めることができるとは限らない。表Tがイクタ君の調査と矛盾せず、Tが定義されるような塔の高さの組み合わせが存在するときTを正しい表と呼ぶことにする。正しい表として何通りのものが考えられるかを計算してイクタ君に教えて欲しい。

ただし、比較された２つの塔の高さは互いに異なるがすべての塔の高さが互いに異なるとは限らない。

Input

入力は以下の形式で与えられる。

N
a₁ b₁
...
a_N-1 b_N-1

Nは塔の数を表す。 a_i, b_i (1 \leq i \leq N - 1)は塔a_iが塔b_iより高いことを表す。

Constraints

入力中の各変数は以下の制約を満たす。

1 \leq N \leq 200
0 \leq a_i, b_i < N
a_i \neq b_i
異なる塔が同じ高さであることもある。
イクタ君の調査結果自体が矛盾していることはなく、少なくとも1つイクタ君の調査結果と矛盾しない表Tが存在する。

Output

考えられる正しい表Tの個数の数を1,000,000,007で割ったあまりを出力せよ。

Sample Input 1

3
0 1
1 2

Output for the Sample Input 1

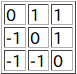
正しい表Tは上図の1通りである。

Sample Input 2

3 
0 1
0 2

Output for the Sample Input 2

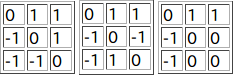
正しい表Tは上図の3通りである。

Sample Input 3

Output for the Sample Input 3

正しい表Tは上図の1通りである。

Sample Input 4

Output for the Sample Input 4

F - Phutball

実行時間制限: 2 sec / メモリ制限: 128 MB

負けず嫌いのイクタ君は、最近囲碁盤を使って遊ぶゲームに熱中している。

しかし、囲碁も五目並べも友人に全く勝てないので、あまり有名でない Phutball というゲームの特訓をすることにした。

このゲームは難しいゲームなので、手始めに自分のターンに勝って終局できるかを判定できるように特訓することにした。

ゲームの勝利条件は以下のようなものである。

白石は黒石の置かれている場所にジャンプすることは出来ない。

碁盤の中央の 19 \times 15 の部分を用いる。
勝利条件を判定したい碁盤は白石が1つと黒石がいくつか置かれた状態で与えられる。
ゴール地点というのは碁盤の下端か、その下側を指す。（下図を参照せよ。）
ゴール地点に白石を運べば勝利する。
勝利するために以下のようなことを行う。
- 白石は1回以上ジャンプを行うことができる。
- ジャンプは白石に隣接する8方向（上下左右と斜め上、斜め下）の黒石のどれかを飛び越えることで行える。
- 黒石が隣接していない方向へジャンプすることは出来ない。
- 飛び越えられた黒石は、1回のジャンプごとに碁盤の上から取り除かれる。
- ジャンプしたあとの白石はゴール地点かゲーム盤の上に存在しなければいけない。
- 黒石が2個以上連続していても、ちょうどそれをまたぐようにジャンプできる。
- 白石は黒石の置かれている場所にジャンプすることは出来ない。(ジャンプする方向に連続している黒石は必ず飛び越えなくてはならない。)

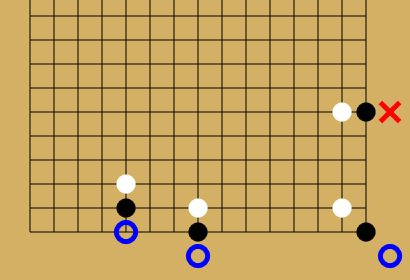
図の丸印がついている場所へはジャンプすることが可能であり、全てゴール地点であるが、バツ印の場所はゴール地点でもなく、碁盤の内側でもないので、ジャンプすることは出来ない。

あなたの仕事はイクタ君の特訓を手助けするために、ゴールできるかどうかの判定と、ゴールするための最小のジャンプ回数を求めるプログラムを書いてあげる事である。

Input

.OXで構成された19\times 15の盤面が19行で与えられる。各行は必ず15文字からなり、各文字は次を表す。

"."は空白を表す。
"O"は白石を表す。
"X"は黒石を表す。

Constraints

黒石の数が20以下。
白石は必ず1つだけ存在する。
すでにゴールした状態が入力されることはない。

Output

ゴール可能なら最短の手数を1行に出力せよ。ゴールすることが不可能な場合は-1を出力せよ。

Sample Input 1

...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
......O........
......X........

Output for the Sample Input 1

白石は黒石を1回ジャンプしてゴールすることができる。

Sample Input 2

...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
......O........
...............

Output for the Sample Input 2

-1

白石は移動できないのでゴールできない。

Sample Input 3

...............
...............
...............
...............
...............
...............
...............
...............
...........O...
............X..
.............X.
.............X.
.............X.
...............
..............X
.........X.....
.............X.
......X....X..X
.....X.X.XX.X..

Output for the Sample Input 3

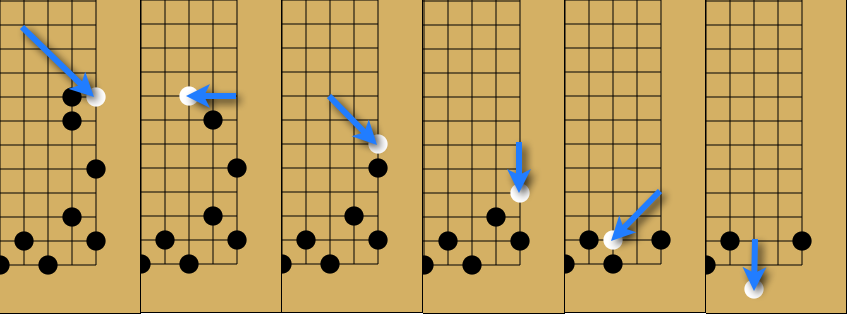
ちょうど6回でゴールできる。

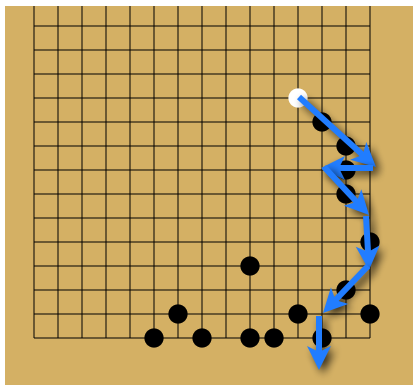
ジャンプ毎に分解した画像を以下に示す。

Sample Input 4

...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
...............
.....XX........
.....XXXO......
......X........

Output for the Sample Input 4

G - Unordered Operators

実行時間制限: 2 sec / メモリ制限: 128 MB

Unordered Operators

小学生のイクタ君は、ある日おじいさんから数式が書かれた紙をもらった。どうやらおじいさんは数式の答えの金額だけお小遣いをくれるらしい。イクタ君はまだ足し算、引き算、掛け算しか習ってなかったので、数式にも足し算と引き算と掛け算しか使われていない。通常の計算では足し算と引き算より掛け算を先に計算しなければならないのだが、イクタ君は演算子の優先順位についての理解があやふやだったので、とりあえず数式の計算結果が最大になるような都合の良い優先順位を考えることにした。

+-×の3つの二項演算子と括弧を含む数式が与えられる。 3つの演算子の優先順位を任意に変更して、数式を最大化したときの計算結果を答えよ。

ただし、以下の点に注意せよ。

演算子は必ず左結合である。 (同じ優先順位の演算子は必ず数式の左側から計算する。)
異なる演算子が同じ優先順位であってもよい。
一つの数式を計算している途中で優先順位を変更してはならない。

Input

入力は以下の形式で与えられる。
0〜9の数字と演算子'+','-','*'、括弧'(',')'で構成された数式

正確に記述すると入力は以下のBNFで示される形式になっている

<expr> ::= ( <expr> ) | <number> | <expr> <op> <expr>
<op> ::= + | - | *

<number>は非負整数を表す。

Constraints

入力は以下の制約を満たす。

数式は200文字以下である。
どのような優先順位を設定しても、計算の結果やその途中で64bit整数型でoverflowするようなことはない。

Output

数式から得られる最大値を1行で出力せよ。

Sample Input 1

3-2*3

Output for the Sample Input 1

*の優先順位を-より低くすることでこのようになる。

Sample Input 2

(5-3*4)*(0-2+1)

Output for the Sample Input 2

優先順位は+>*>-

Sample Input 3

1-2+3-4+5-6*0

Output for the Sample Input 3

優先順位が一般的な場合

Sample Input 4

(1989967-3*1-211+4487)

Output for the Sample Input 4

8511076028

H - Almost Same Substring

実行時間制限: 4 sec / メモリ制限: 128 MB

不運なイクタ君は持っていた大事な文字列Tをウィルスによって異なる文字列T'に書き換えられてしまった。そのウィルスがTの１文字を異なる文字に書き換えてしまったことがわかっている。すなわちTとT'はちょうど１文字のみ異なっている。イクタ君はTを復元するために、Tが出現していると思われる文書Sを用意した。Tを復元するための下準備としてSの部分文字列でTと一致している可能性があるものの個数を調べたい。

文字列T'と文書Sが与えられる。 S = a₁ a₂ a₃ ... a_|S|の長さ|T'|の部分文字列a_k a_k+1 ... a_k+|T'|-1(1 \leq k \leq |S| - |T'| + 1) でT'と比較して1文字だけ異なるものの数を求めよ。

Input

入力は以下の形式で与えられる。

S
T'

１行目でSが与えられる。
２行目でT'が与えられる。
S, T'はそれぞれ大文字、小文字のアルファベットのみからなる。

Constraints

入力中の各変数は以下の制約を満たす。

1 \leq |S| \leq 300,000
1 \leq |T'| \leq |S|

Output

条件を満たす部分文字列の数を1行に出力せよ。

Sample Input 1

abcbcdbc
abc

Output for the Sample Input 1

Sの3番目の文字から始まるcbc, Sの6番目の文字から始まるdbcが条件を満たす。

Sample Input 2

aaaaaa
aaaaaa

Output for the Sample Input 2

完全に一致する文字列は数えてはならない。

Sample Input 3

baaaaaaaa
b

Output for the Sample Input 3

I - A + B

実行時間制限: 8 sec / メモリ制限: 128 MB

プログラミングコンテストの合宿で出す問題のアイディアが出ずに困っていたイクタ君は、ある日友人に相談した。

イクタ君「こういうアルゴリズムを使わないと解けないような問題が出したいんですけど、なにかありませんかね？」

友人「それではこういうものを考えたらいいんじゃないですか」

このようにしてその友人は以下のような問題の原案となるアイデアを考えてくれた。

2進数A,Bが与えられた時、以下の様なクエリを処理せよ。

出力クエリ: max{x を2進数で表したときの、1の数 | A \leq x < A+B }を出力
A変更クエリ: Aの最下位ビットからiビット目(0-origin)を反転
B変更クエリ: Bの最下位ビットからiビット目(0-origin)を反転

iビット目というのが 0-origin で表されていることに注意せよ。つまり、Aの最下位ビットから0ビット目とは最下位ビットを表す。

Input

入力は以下の形式で与えられる。

N A B
Q₁
...
Q_N

1行目にクエリの数N,2進数A, Bが与えられる。

2～N+1行目には以下の様なクエリが与えられる。

Q
A i
B i

Qが出力クエリを、A i,B iはそれぞれAの最下位ビットからiビット目、Bの最下位ビットからiビット目を反転させる変更クエリを表している。

Constraints

入力中の各変数は以下の制約を満たす。

1 \leq N < 300,000
1 \leq |A|,|B| \leq 300,000 (|A|はAの長さ)
A i というクエリでは 0 \leq i < |A|
B i というクエリでは 0 \leq i < |B|
Bが0になることはない

Output

出力クエリごとに答えを1行に出力せよ。

Sample Input 1

4 10000 00101
Q
A 0
B 1
Q

Output for the Sample Input 1

3
4

最初の出力クエリでは A=10000, B=00101, A+B=10101なので求めるxは10011

次の出力クエリでは A=10001, B=00111, A+B=11000なので求めるxは10111

Sample Input 2

9 0110111101 0010100111
Q
B 4
Q
A 4
Q
B 9
Q
A 8
Q

Output for the Sample Input 2

J - くるくるくるりん

実行時間制限: 12 sec / メモリ制限: 128 MB

ヘリリンは二次元平面上における長さ2Lの線分の形状をしている。
ヘリリンのまわりには、線分の形状をしたいくつかの障害物が存在している。

ヘリリンは障害物に接すると体力が削られてしまう。
完璧主義のヘリリンは無傷でゴールすることにした。

ヘリリンは以下の行動ができる。

平行移動
ヘリリンを表す線分の中点を中心として、反時計周りにちょうど 180 / r 度だけ回転する

ただし、二次元平面は上方向にy軸をとる。

ヘリリンのまわりに、2 点 S, G がある。
始めはヘリリンの中心は点 S にあって、x軸に平行な状態になっている。

ヘリリンは、平行移動するのは得意だが、回転するのは不得意である。
あなたの仕事は、ヘリリンが中心を点 S から点 G まで移動させるまでに必要な、最小の回転行動の回数を求めることである。
移動させることができない場合は、そのことも検出せよ。

ただし、以下のことに注意せよ。

ヘリリンは移動しながら回転することはできない。
ヘリリンが回転する途中で障害物にぶつかりうる場合は、回転することはできない。
障害物が互いに交差していることはあり得る。
線分は十分小さい有限の太さを持つものとして扱う。最後のサンプルを見よ。

Input

入力は以下の形式で与えられる。

L r
s_x s_y
g_x g_y
n
x₁₁ y₁₁ x₁₂ y₁₂
...
x_n1 y_n1 x_n2 y_n2

Lはヘリリンの半分の長さを表す。 rは回転角度を定めるものである。 (s_x, s_y)は点 S、(g_x, g_y)は点 G の座標である。 nは障害物の数を表す。 (x_i1, y_i1)と(x_i2, y_i2)はi番目の障害物を表す線分の端点である。

Constraints

入力は以下の制約を満たす。

1 \leq n \leq 30
2\leq r \leq 11
1 \leq L \leq 10⁵
入力に含まれる座標の各成分は絶対値が10⁵以下
入力に含まれる数値はすべて整数
i = 1, ..., nについて (x_i1, y_i1) \neq (x_i2, y_i2)
ヘリリンをスタート地点にx軸に水平な状態で配置したとき、障害物との（線分と線分との）距離は 10^-3 より大きい
障害物を表す線分の端点を、両方向に 10^-3 だけ延ばしても縮めても解は変わらない
Lを 10^-3 だけ増減させても解は変わらない
障害物の線分をl_iと書くことにすると、1 \leq i \leq j \leq nであって、l_iとl_jの距離が2L以下であるような組(i, j)は高々100個
ゴール地点は障害物に乗っていることはない

Output

スタート地点からゴール地点まで移動するために必要な最小の回転行動の回数を1行に出力せよ。移動させることができない場合は、-1を1行に出力せよ。

Sample Input 1

Output for the Sample Input 1

ヘリリンを90度回転させることで、隙間を抜けることができる。

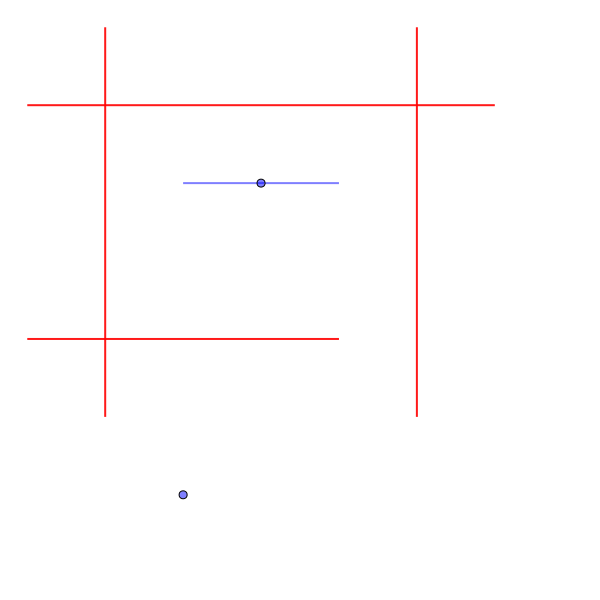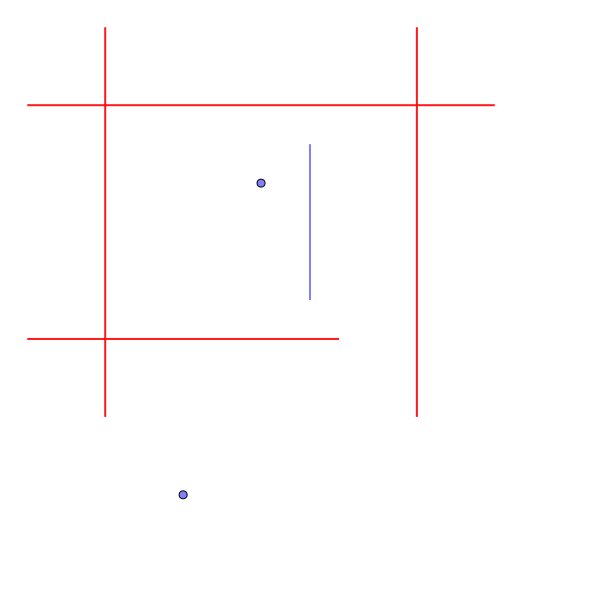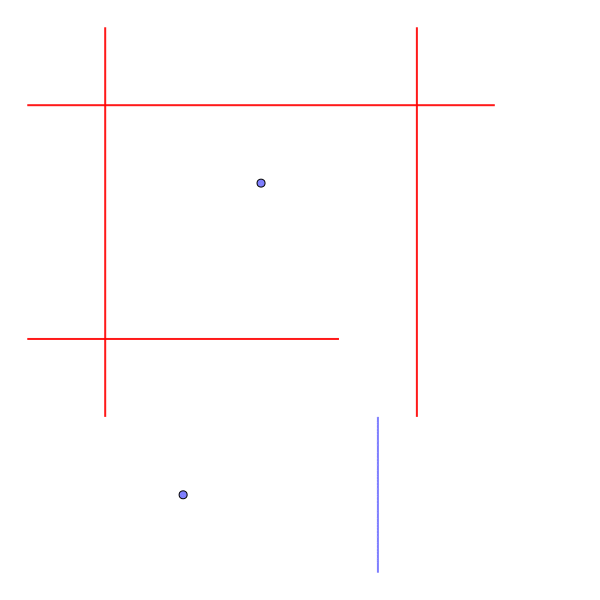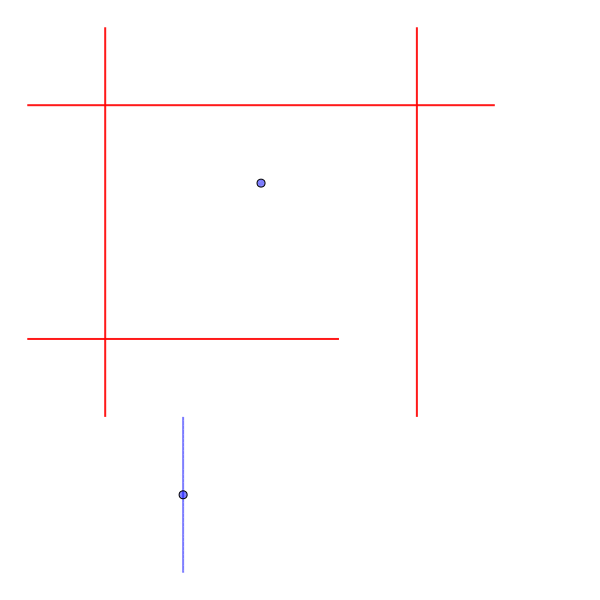
Sample Input 2

Output for the Sample Input 2

-1

ヘリリンは完全に囲まれているので、ゴールまで移動することができない。

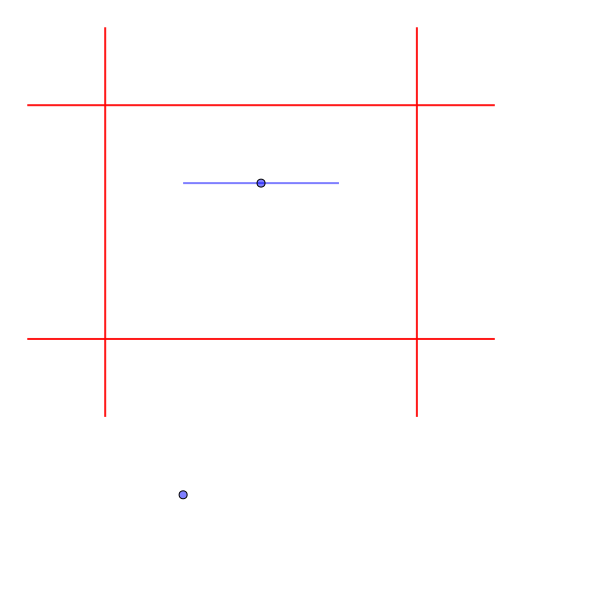
Sample Input 3

Output for the Sample Input 3

斜めの経路を通るためには、3回反時計周りに回転しなければならない。

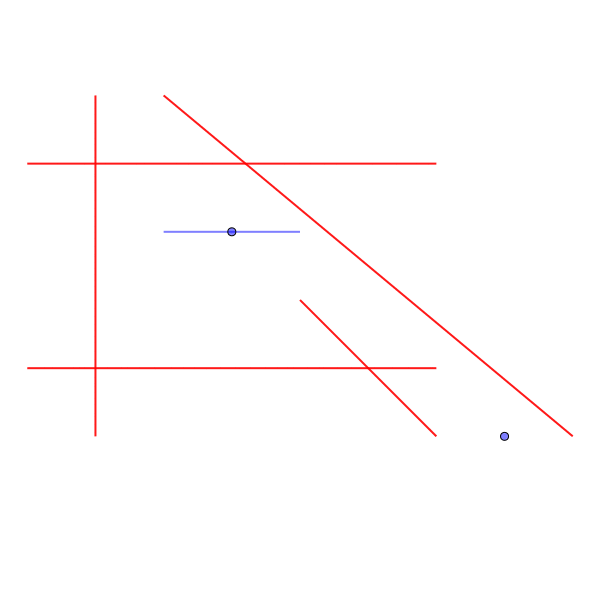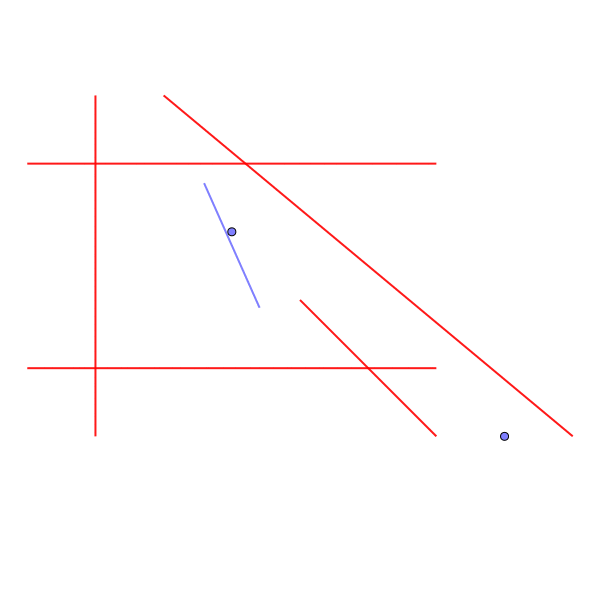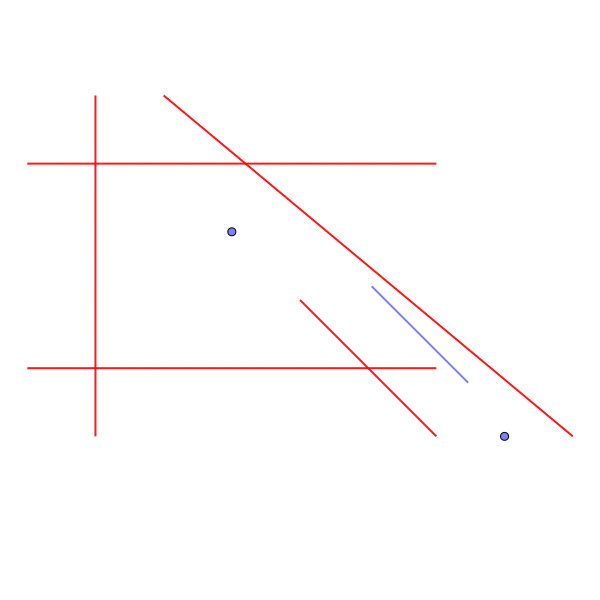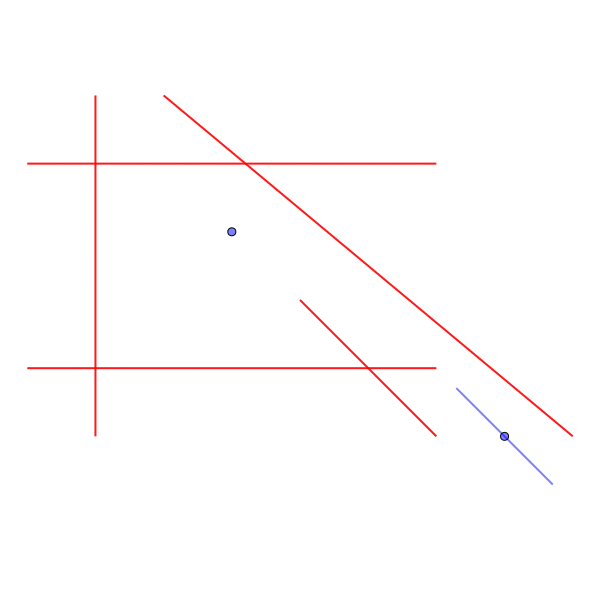
Sample Input 4

Output for the Sample Input 4

-1

ヘリリンは障害物にぴったり接することができないので、隙間のところで回転してゴールまで移動することはできない。

K - Air Pollution

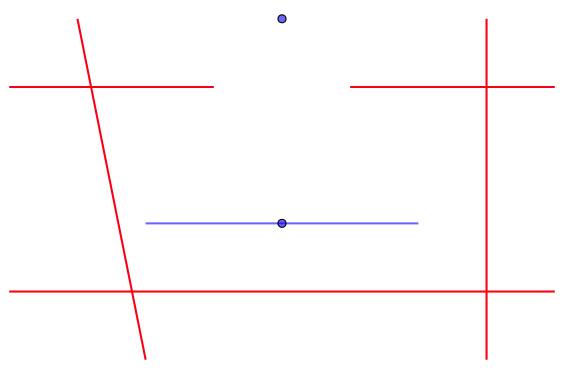
実行時間制限: 2 sec / メモリ制限: 128 MB

20XX年, ICPC (Ikuta's Computer Pollutes Community) 商店街の経営者たちは大気汚染に悩まされていた。かつての活気を取り戻すためにも大気の綺麗さを一定以上にしなければならない。

商店街の店は一列に並んでおり、1からnで番号付けられている。現在、おのおのの店のまわりの大気の綺麗さは p_i である。あなたは2からn-1番目の店を選んで、その周辺の大気を循環させることで, その店と周囲の店の大気の綺麗さを変更することができる。正確にいうと, i ( 2 \leq i \leq n-1 )番目を選んだとき、p_i-1とp_i+1にはp_iだけ加算され, 逆にp_iには2p_iだけ減算される。つまり、新しい大気の綺麗さp'は,

p'_i-1 = p_i-1 + p_i
p'_i = p_i - 2 p_i
p'_i+1 = p_i+1 + p_i となる。この操作を繰り返して、すべての店の大気の綺麗さp_iを、許容できる最低限の大気の綺麗さ l_i 以上にすることが目的である。

大気を循環させるためには多大な費用がかかるため、なるべく少ない回数で達成したい。 ICPC商店街の未来のためにも力を貸してほしい。

Input

入力は以下の形式で与えられる。

n
p₁ ... p_n
l₁ ... l_n

nは店の数、p_iはi番目の店の現在の大気の綺麗さ、l_iはi番目の店が達成すべき大気の綺麗さを表す。

Constraints

入力中の各変数は以下の制約を満たす。

3 \leq n \leq 10⁵
-10⁸ \leq p_i \leq 10⁸
1 \leq l_i \leq 10⁸

Output

すべての店が大気の綺麗さを達成するために必要な大気を循環させる回数の最小値を1行に出力せよ。

どのように操作しても達成できない場合には-1を出力せよ。

Sample Input 1

3
3 -1 4
2 1 3

Output for the Sample Input 1

店2を選ぶことで, 店1,2,3の大気の綺麗さはそれぞれ2, 1, 3となる。

Sample Input 2

3
3 -1 4
2 1 5

Output for the Sample Input 2

-1

どのように操作しても店3が大気の綺麗さを達成できない。

Sample Input 3

4
3 -1 -1 3
1 1 1 1

Output for the Sample Input 3

店2, 店3, 店2の順番で大気を循環させると達成することができる。

L - 京都旅行

実行時間制限: 2 sec / メモリ制限: 128 MB

この問題の不備は修正されましたので、回答を提出してください。ご迷惑をおかけしてもうしわけございませんでした。

キョウトという街は古い寺社仏閣で有名な観光地である。

イクタ君は数人の友人とキョウト観光に来ていたが、全員が好き勝手に行動した結果、みんな迷子になってしまった。

そこでイクタ君は、なるべく早く全員と合流するためには集合場所をどこにするのがよいか考えることにした。

キョウトの道路は東西と南北に距離10の間隔で無数に走っており、無限に広がる正方格子とみなすことができる。

道路は直線であるとみなし、幅は無いものとする。また、街の中心を基準として東に距離x、北に距離y移動した位置を(x,y)という座標で表す。

街の中心である(0,0)では東西の道路と南北の道路が交差している。

下図はキョウトの道路と、いくつかの点の座標を図示したものである。

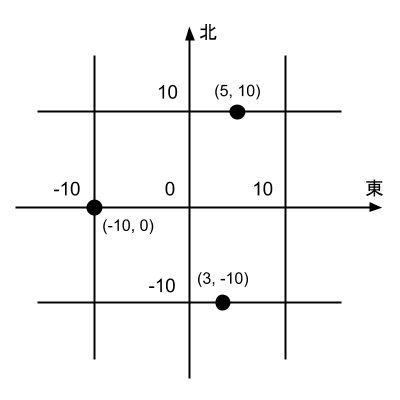
N人の観光客の座標(X_i,Y_i)が整数で与えられるので、N人が道路上を移動して1点に集合するのに必要な時間の最小値を答えよ。

観光客は時間1あたり距離1の速さで連続的に道路上を動くことができるとする。

与えられるN人の観光客の座標はそれぞれ相異なり、また全ての座標は道路上にあることが保証されている。

また、複数の観光客が同時に1点に存在したり、観光客同士がすれ違うように移動することも可能であるとする。

Input

入力は以下の形式で与えられる。

N
X₁ Y₁
...
X_N Y_N

1行目のNは観光客の人数である。次のN行のうちi行目(1\leq i \leq N)はi番目の観光客の位置(X_i, Y_i)を表している。 X_i,Y_iはそれぞれ整数で与えられる。

Constraints

入力中の各変数は以下の制約を満たす。

2 \leq N \leq 10000
-10⁸ \leq X_i, Y_i \leq 10⁸
i \neq j のとき (X_i, Y_i) \neq (X_j, Y_j)
X_i と Y_i のうち少なくとも一方は10の倍数である

Output

問題の解を1行に出力せよ。 10^-3までの絶対誤差を許容する。

Sample Input 1

Output for the Sample Input 1

(0, 1)に集合すればよい（この入力例は問題文中の図と対応している）

Sample Input 2

2
0 0
0 1

Output for the Sample Input 2

0.5

(0, 0.5)に集合すればよい（整数座標以外に集まる場合もあることに注意せよ）

Sample Input 3

4
100000000 100000000
100000000 -100000000
-100000000 100000000
-100000000 -100000000

Output for the Sample Input 3

200000000