実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 100 点
問題文
縦 H 行、横 W 列のマス目があります。
上から i 行目、左から j 列目には長さ 5 の文字列 S_{i,j} が書かれています。
行には上から順に 1~H の番号が、列には左から順に A~Z の番号がついています。

この中から snuke という文字列を探し、列と行の番号を順に続けて出力してください。
例えば 6 行目の 8 列目にあった場合は、H6 のように出力してください。
制約
- 1≦H, W≦26
- S_{i,j} は小文字アルファベット(
a-z)のみからなる長さ 5 の文字列である。 - 与えられる文字列のうち、ちょうど 1 つだけが
snukeである。
入力
入力は以下の形式で標準入力から与えられる。
H W
S_{1,1} S_{1,2} ... S_{1,W}
S_{2,1} S_{2,2} ... S_{2,W}
:
S_{H,1} S_{H,2} ... S_{H,W}
出力
snuke という文字列が書かれているマスの列と行の番号を続けて出力せよ。
入力例 1
15 10 snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snuke snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake
出力例 1
H6
入力例 2
1 1 snuke
出力例 2
A1
Score : 100 points
Problem Statement
There is a grid with H rows and W columns.
The square at the i-th row and j-th column contains a string S_{i,j} of length 5.
The rows are labeled with the numbers from 1 through H, and the columns are labeled with the uppercase English letters from A through the W-th letter of the alphabet.

Exactly one of the squares in the grid contains the string snuke. Find this square and report its location.
For example, the square at the 6-th row and 8-th column should be reported as H6.
Constraints
- 1≦H, W≦26
- The length of S_{i,j} is 5.
- S_{i,j} consists of lowercase English letters (
a-z). - Exactly one of the given strings is equal to
snuke.
Input
The input is given from Standard Input in the following format:
H W
S_{1,1} S_{1,2} ... S_{1,W}
S_{2,1} S_{2,2} ... S_{2,W}
:
S_{H,1} S_{H,2} ... S_{H,W}
Output
Print the labels of the row and the column of the square containing the string snuke, with no space inbetween.
Sample Input 1
15 10 snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snuke snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake snake
Sample Output 1
H6
Sample Input 2
1 1 snuke
Sample Output 2
A1
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 300 点
問題文
ある年のCODE FESTIVALの決勝では N 問の問題が出題されました。
i (1≦i≦N) 番目の問題の配点は i 点です。
高橋くんは、このコンテストでちょうど N 点を取りたいと思い、そのために解く問題の集合をどうするかを考えています。
配点が高い問題は難しいので、解く問題の配点のうちの最大値が最小になるようにしようと考えました。
高橋くんが解くべき問題の集合を求めてください。
制約
- 1≦N≦10^7
部分点
- 1≦N≦1000 を満たすデータセットに正解した場合は、200 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 100 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N
出力
点数の合計がちょうど N となるような集合のうち、配点の最大値が最小となるようなものを求め、その集合に含まれる問題の番号を 1 行にひとつずつ出力せよ。昇順に出力する必要はありません。
そのような集合が複数考えられる場合は、いずれを出力しても構わない。
入力例 1
4
出力例 1
1 3
4 番目の問題のみを解いた場合もちょうど 4 点が得られますが、1,3 番目の問題を解く方が配点の最大値が小さくなります。
入力例 2
7
出力例 2
1 2 4
\{3,4\} という集合も考えられます。
入力例 3
1
出力例 3
1
Score : 300 points
Problem Statement
The problem set at CODE FESTIVAL 20XX Finals consists of N problems.
The score allocated to the i-th (1≦i≦N) problem is i points.
Takahashi, a contestant, is trying to score exactly N points. For that, he is deciding which problems to solve.
As problems with higher scores are harder, he wants to minimize the highest score of a problem among the ones solved by him.
Determine the set of problems that should be solved.
Constraints
- 1≦N≦10^7
Partial Score
- 200 points will be awarded for passing the test set satisfying 1≦N≦1000.
- Additional 100 points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
N
Output
Among the sets of problems with the total score of N, find a set in which the highest score of a problem is minimum, then print the indices of the problems in the set in any order, one per line.
If there exists more than one such set, any of them will be accepted.
Sample Input 1
4
Sample Output 1
1 3
Solving only the 4-th problem will also result in the total score of 4 points, but solving the 1-st and 3-rd problems will lower the highest score of a solved problem.
Sample Input 2
7
Sample Output 2
1 2 4
The set \{3,4\} will also be accepted.
Sample Input 3
1
Sample Output 3
1
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 400 点
問題文
ある星には M 種類の言語があり、1 \sim M の番号が付けられています。
この星のある年のCODE FESTIVALには星中から N 人の参加者が集まりました。
i (1≦i≦N) 人目の参加者は K_i 種類の言語 L_{i,1}, L_{i,2}, ..., L_{i,{}K_i} を話すことが出来ます。
ある 2 人は以下のいずれかの条件を満たすときに限り、コミュニケーションを取ることが出来ます。
- 2 人ともが話すことの出来る言語が存在する。
- ある人 X が存在して、 2 人ともが X とコミュニケーションを取ることが出来る。
このとき、N 人すべての参加者が他のすべての参加者とコミュニケーションを取ることが出来るかどうかを判定してください。
制約
- 2≦N≦10^5
- 1≦M≦10^5
- 1≦K_i≦M
- K_iの総和≦10^5
- 1≦L_{i,j}≦M
- L_{i,1}, L_{i,2}, ..., L_{i,{}K_i} は相異なる。
部分点
- N≦1000 かつ M≦1000 かつ K_iの総和≦1000 を満たすデータセットに正解した場合は、200 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 200 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N M
K_1 L_{1,1} L_{1,2} ... L_{1,{}K_1}
K_2 L_{2,1} L_{2,2} ... L_{2,{}K_2}
:
K_N L_{N,1} L_{N,2} ... L_{N,{}K_N}
出力
N 人すべての参加者が他のすべての参加者とコミュニケーションを取ることが出来るなら YES を、そうでないなら NO を出力せよ。
入力例 1
4 6 3 1 2 3 2 4 2 2 4 6 1 6
出力例 1
YES
以下のように、任意の 2 人がコミュニケーションをとることが出来ます。
- 人 1 と人 2:共通の言語 2 を話せます。
- 人 2 と人 3:共通の言語 4 を話せます。
- 人 1 と人 3: 2 人とも人 2 とコミュニケーションを取ることができます。
- 人 3 と人 4:共通の言語 6 を話せます。
- 人 2 と人 4: 2 人とも人 3 とコミュニケーションを取ることができます。
- 人 1 と人 4: 2 人とも人 2 とコミュニケーションを取ることができます。
また、誰も話すことの出来ない言語が存在する可能性があることに注意してください。
入力例 2
4 4 2 1 2 2 1 2 1 3 2 4 3
出力例 2
NO
例えば、人 1 と人 3 はコミュニケーションを取ることができません。
Score : 400 points
Problem Statement
On a planet far, far away, M languages are spoken. They are conveniently numbered 1 through M.
For CODE FESTIVAL 20XX held on this planet, N participants gathered from all over the planet.
The i-th (1≦i≦N) participant can speak K_i languages numbered L_{i,1}, L_{i,2}, ..., L_{i,{}K_i}.
Two participants A and B can communicate with each other if and only if one of the following conditions is satisfied:
- There exists a language that both A and B can speak.
- There exists a participant X that both A and B can communicate with.
Determine whether all N participants can communicate with all other participants.
Constraints
- 2≦N≦10^5
- 1≦M≦10^5
- 1≦K_i≦M
- (The sum of all K_i)≦10^5
- 1≦L_{i,j}≦M
- L_{i,1}, L_{i,2}, ..., L_{i,{}K_i} are pairwise distinct.
Partial Score
- 200 points will be awarded for passing the test set satisfying the following: N≦1000, M≦1000 and (The sum of all K_i)≦1000.
- Additional 200 points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
N M
K_1 L_{1,1} L_{1,2} ... L_{1,{}K_1}
K_2 L_{2,1} L_{2,2} ... L_{2,{}K_2}
:
K_N L_{N,1} L_{N,2} ... L_{N,{}K_N}
Output
If all N participants can communicate with all other participants, print YES. Otherwise, print NO.
Sample Input 1
4 6 3 1 2 3 2 4 2 2 4 6 1 6
Sample Output 1
YES
Any two participants can communicate with each other, as follows:
- Participants 1 and 2: both can speak language 2.
- Participants 2 and 3: both can speak language 4.
- Participants 1 and 3: both can communicate with participant 2.
- Participants 3 and 4: both can speak language 6.
- Participants 2 and 4: both can communicate with participant 3.
- Participants 1 and 4: both can communicate with participant 2.
Note that there can be languages spoken by no participant.
Sample Input 2
4 4 2 1 2 2 1 2 1 3 2 4 3
Sample Output 2
NO
For example, participants 1 and 3 cannot communicate with each other.
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 700 点
問題文
高橋君は N 枚のカードで遊んでいます。
i 枚目のカードには整数 X_i が書かれています。
高橋君は以下のいずれかの条件を満たすカードの2 枚組をなるべくたくさん作ろうとしています。
- 2 枚のカードに書かれた整数が同じである。
- 2 枚のカードに書かれた整数の和が M の倍数である。
高橋君が作ることの出来る組の個数の最大値を求めなさい。
ただし、1 枚のカードを複数の組で使うことはできないものとします。
制約
- 2≦N≦10^5
- 1≦M≦10^5
- 1≦X_i≦10^5
入力
入力は以下の形式で標準入力から与えられる。
N M X_1 X_2 ... X_N
出力
高橋君が作ることの出来る組の個数の最大値を出力せよ。
入力例 1
7 5 3 1 4 1 5 9 2
出力例 1
3
(3,2), (1,4), (1,9) の 3 組を作ることが出来ます。
(3,2), (1,1) のように組を作ることもできますが、これでは組の個数が最大とならないことに注意してください。
入力例 2
15 10 1 5 6 10 11 11 11 20 21 25 25 26 99 99 99
出力例 2
6
Score : 700 points
Problem Statement
Takahashi is playing with N cards.
The i-th card has an integer X_i on it.
Takahashi is trying to create as many pairs of cards as possible satisfying one of the following conditions:
- The integers on the two cards are the same.
- The sum of the integers on the two cards is a multiple of M.
Find the maximum number of pairs that can be created.
Note that a card cannot be used in more than one pair.
Constraints
- 2≦N≦10^5
- 1≦M≦10^5
- 1≦X_i≦10^5
Input
The input is given from Standard Input in the following format:
N M X_1 X_2 ... X_N
Output
Print the maximum number of pairs that can be created.
Sample Input 1
7 5 3 1 4 1 5 9 2
Sample Output 1
3
Three pairs (3,2), (1,4) and (1,9) can be created.
It is possible to create pairs (3,2) and (1,1), but the number of pairs is not maximized with this.
Sample Input 2
15 10 1 5 6 10 11 11 11 20 21 25 25 26 99 99 99
Sample Output 2
6
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1000 点
問題文
りんごさんはクッキーを焼いています。
りんごさんははじめ、1 秒間に 1 枚のクッキーを焼くことができます。
りんごさんはクッキーを食べることができます。 まだ食べていないクッキーが全部で x 枚あるとき、りんごさんはそれらをすべて食べることにより、1 秒間に焼くことのできるクッキーの枚数がちょうど x 枚になります。 クッキーを一部だけ食べることはできず、食べるときはすべて食べなければなりません。 クッキーを食べるためには個数にかかわらず A 秒の時間がかかり、その間はクッキーを焼くことができません。 また、クッキーは 1 秒ごとに同時に焼きあがるため、例えば 0.5 秒で x/2 枚のクッキーを焼くというようなことはできません。
りんごさんは N 枚のクッキーをおばあさんにプレゼントしたいと思っています。 りんごさんがまだ食べていないクッキーを N 枚以上用意するためにかかる時間の最小値を求めてください。
制約
- 1≦N≦10^{12}
- 0≦A≦10^{12}
- A は整数である。
部分点
- N≦10^6 かつ A≦10^6 を満たすデータセットに正解した場合は、500 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 500 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N A
出力
りんごさんがまだ食べていないクッキーを N 枚以上用意するためにかかる時間の最小値を出力せよ。
入力例 1
8 1
出力例 1
7
以下のように行動すると、7 秒で 8 枚のクッキーを用意することができます。
- 1 秒後:1 枚のクッキーが焼きあがる。
- 2 秒後:1 枚のクッキーが焼きあがり、合計枚数が 2 枚となる。ここで、2 枚のクッキーをすべて食べる。
- 3 秒後:クッキーを食べ終わり、1 秒間に 2 枚のクッキーを焼くことができるようになる。
- 4 秒後:2 枚のクッキーが焼きあがる。
- 5 秒後:2 枚のクッキーが焼きあがり、合計枚数が 4 枚となる。
- 6 秒後:2 枚のクッキーが焼きあがり、合計枚数が 6 枚となる。
- 7 秒後:2 枚のクッキーが焼きあがり、合計枚数が 8 枚となる。
入力例 2
1000000000000 1000000000000
出力例 2
1000000000000
入力例 3
123456 7
出力例 3
78
Score : 1000 points
Problem Statement
Rng is baking cookies.
Initially, he can bake one cookie per second.
He can also eat the cookies baked by himself. When there are x cookies not yet eaten, he can choose to eat all those cookies. After he finishes eating those cookies, the number of cookies he can bake per second becomes x. Note that a cookie always needs to be baked for 1 second, that is, he cannot bake a cookie in 1/x seconds when x > 1. When he choose to eat the cookies, he must eat all of them; he cannot choose to eat only part of them. It takes him A seconds to eat the cookies regardless of how many, during which no cookies can be baked.
He wants to give N cookies to Grandma. Find the shortest time needed to produce at least N cookies not yet eaten.
Constraints
- 1≦N≦10^{12}
- 0≦A≦10^{12}
- A is an integer.
Partial Score
- 500 points will be awarded for passing the test set satisfying N≦10^6 and A≦10^6.
- Additional 500 points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
N A
Output
Print the shortest time needed to produce at least N cookies not yet eaten.
Sample Input 1
8 1
Sample Output 1
7
It is possible to produce 8 cookies in 7 seconds, as follows:
- After 1 second: 1 cookie is done.
- After 2 seconds: 1 more cookie is done, totaling 2. Now, Rng starts eating those 2 cookies.
- After 3 seconds: He finishes eating the cookies, and he can now bake 2 cookies per second.
- After 4 seconds: 2 cookies are done.
- After 5 seconds: 2 more cookies are done, totaling 4.
- After 6 seconds: 2 more cookies are done, totaling 6.
- After 7 seconds: 2 more cookies are done, totaling 8.
Sample Input 2
1000000000000 1000000000000
Sample Output 2
1000000000000
実行時間制限: 3 sec / メモリ制限: 256 MiB
配点 : 1000 点
問題文
高橋王国には N 個の町があり、それぞれの町には 1~N の番号が付けられています。
この国の王様である高橋くんは、N 個の町を M 日間かけて廻る出張を計画しています。計画では、町の列 c を決め、i (1≦i≦M) 日目には町 c_i へ行くことにしました。すなわち、i 日目には、今いる町から町 c_i へ移動します。ただし、今いる町が町 c_i であった場合は移動しません。高橋くんははじめ町 1 にいるものとします。
困ったことに、この国には道路が 1 本もありません。しかたがないので高橋くんは、道路を作りながら歩くことにしました。高橋くんが町 a から町 b へ移動すると、町 a から町 b への一方通行の道路ができます。
高橋くんは国民思いの王様なので、出張の最終日の目的地に着いた直後に「どの町からどの町へも、高橋くんが作った道路を辿ることによって移動することが出来る」という条件を満たすようにしたいと考えました。このような条件を満たす町の列 c は何通り考えられるでしょうか?
制約
- 2≦N≦300
- 1≦M≦300
入力
入力は以下の形式で標準入力から与えられる。
N M
出力
答えを 1000000007 (=10^9+7) で割った余りを出力せよ。
入力例 1
3 3
出力例 1
2
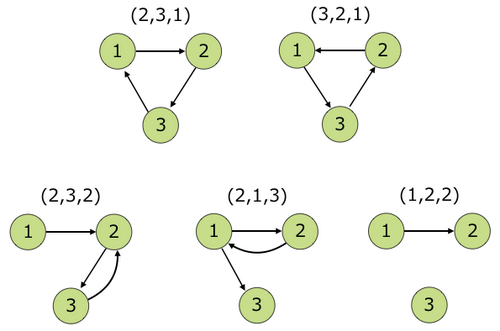
下図のように、c = (2,3,1) または c = (3,2,1) のときのみ条件を満たし、c = (2,3,2) や c = (2,1,3) や c = (1,2,2) などは条件を満たしません。
入力例 2
150 300
出力例 2
734286322
入力例 3
300 150
出力例 3
0
Score : 1000 points
Problem Statement
There are N towns in Takahashi Kingdom. They are conveniently numbered 1 through N.
Takahashi the king is planning to go on a tour of inspection for M days. He will determine a sequence of towns c, and visit town c_i on the i-th day. That is, on the i-th day, he will travel from his current location to town c_i. If he is already at town c_i, he will stay at that town. His location just before the beginning of the tour is town 1, the capital. The tour ends at town c_M, without getting back to the capital.
The problem is that there is no paved road in this kingdom. He decided to resolve this issue by paving the road himself while traveling. When he travels from town a to town b, there will be a newly paved one-way road from town a to town b.
Since he cares for his people, he wants the following condition to be satisfied after his tour is over: "it is possible to travel from any town to any other town by traversing roads paved by him". How many sequences of towns c satisfy this condition?
Constraints
- 2≦N≦300
- 1≦M≦300
Input
The input is given from Standard Input in the following format:
N M
Output
Print the number of sequences of towns satisfying the condition, modulo 1000000007 (=10^9+7).
Sample Input 1
3 3
Sample Output 1
2
As shown below, the condition is satisfied only when c = (2,3,1) or c = (3,2,1). Sequences such as c = (2,3,2), c = (2,1,3), c = (1,2,2) do not satisfy the condition.

Sample Input 2
150 300
Sample Output 2
734286322
Sample Input 3
300 150
Sample Output 3
0
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1300 点
問題文
N 個の頂点からなるグラフがあり、頂点には 0~N-1 の番号が付けられています。辺はまだありません。
辺を追加するクエリを Q 個処理します。 i (1≦i≦Q) 番目のクエリでは A_i, B_i, C_i の 3 つの整数が与えられるので、以下のように辺を無限本追加します。
- A_i 番の頂点と B_i 番の頂点をつなぐ、重み C_i の無向辺を追加する。
- B_i 番の頂点と A_i+1 番の頂点をつなぐ、重み C_i+1 の無向辺を追加する。
- A_i+1 番の頂点と B_i+1 番の頂点をつなぐ、重み C_i+2 の無向辺を追加する。
- B_i+1 番の頂点と A_i+2 番の頂点をつなぐ、重み C_i+3 の無向辺を追加する。
- A_i+2 番の頂点と B_i+2 番の頂点をつなぐ、重み C_i+4 の無向辺を追加する。
- B_i+2 番の頂点と A_i+3 番の頂点をつなぐ、重み C_i+5 の無向辺を追加する。
- A_i+3 番の頂点と B_i+3 番の頂点をつなぐ、重み C_i+6 の無向辺を追加する。
- ...
ただし、頂点番号は mod N で考えます。 たとえば、N 番とは 0 番のことであり、2N-1 番とは N-1 番のことです。
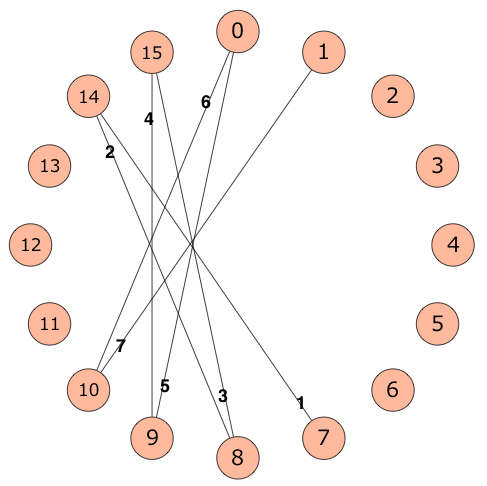
例えば、N=16, A_i=7, B_i=14, C_i=1 のときは下図のように辺を追加します。(図では最初の 7 本のみ)
すべての辺を追加した後のグラフの最小全域木に含まれる辺の重みの和を求めて下さい。
制約
- 2≦N≦200,000
- 1≦Q≦200,000
- 0≦A_i,B_i≦N-1
- 1≦C_i≦10^9
入力
入力は以下の形式で標準入力から与えられる。
N Q A_1 B_1 C_1 A_2 B_2 C_2 : A_Q B_Q C_Q
出力
最小全域木に含まれる辺の重みの和を出力せよ。
入力例 1
7 1 5 2 1
出力例 1
21
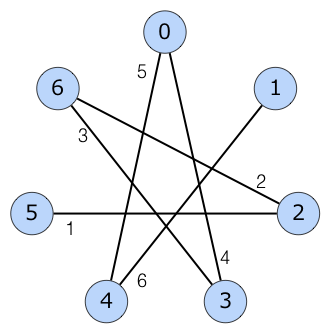
最小全域木は下図のようになります。
多重辺が存在しうることに注意して下さい。
入力例 2
2 1 0 0 1000000000
出力例 2
1000000001
自己ループが存在しうることに注意して下さい。
入力例 3
5 3 0 1 10 0 2 10 0 4 10
出力例 3
42
Score : 1300 points
Problem Statement
We have a graph with N vertices, numbered 0 through N-1. Edges are yet to be added.
We will process Q queries to add edges. In the i-th (1≦i≦Q) query, three integers A_i, B_i and C_i will be given, and we will add infinitely many edges to the graph as follows:
- The two vertices numbered A_i and B_i will be connected by an edge with a weight of C_i.
- The two vertices numbered B_i and A_i+1 will be connected by an edge with a weight of C_i+1.
- The two vertices numbered A_i+1 and B_i+1 will be connected by an edge with a weight of C_i+2.
- The two vertices numbered B_i+1 and A_i+2 will be connected by an edge with a weight of C_i+3.
- The two vertices numbered A_i+2 and B_i+2 will be connected by an edge with a weight of C_i+4.
- The two vertices numbered B_i+2 and A_i+3 will be connected by an edge with a weight of C_i+5.
- The two vertices numbered A_i+3 and B_i+3 will be connected by an edge with a weight of C_i+6.
- ...
Here, consider the indices of the vertices modulo N. For example, the vertice numbered N is the one numbered 0, and the vertice numbered 2N-1 is the one numbered N-1.
The figure below shows the first seven edges added when N=16, A_i=7, B_i=14, C_i=1:

After processing all the queries, find the total weight of the edges contained in a minimum spanning tree of the graph.
Constraints
- 2≦N≦200,000
- 1≦Q≦200,000
- 0≦A_i,B_i≦N-1
- 1≦C_i≦10^9
Input
The input is given from Standard Input in the following format:
N Q A_1 B_1 C_1 A_2 B_2 C_2 : A_Q B_Q C_Q
Output
Print the total weight of the edges contained in a minimum spanning tree of the graph.
Sample Input 1
7 1 5 2 1
Sample Output 1
21
The figure below shows the minimum spanning tree of the graph:

Note that there can be multiple edges connecting the same pair of vertices.
Sample Input 2
2 1 0 0 1000000000
Sample Output 2
1000000001
Also note that there can be self-loops.
Sample Input 3
5 3 0 1 10 0 2 10 0 4 10
Sample Output 3
42
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1600 点
問題文
N 個のマスが一列に並んでおり、左から順に 1~N の番号が付けられています。 すぬけくんとりんごさんはこのマス目を使って、以下のようなボードゲームで遊ぼうとしています。
- はじめに、すぬけくんがすべてのマスに 1 つずつ整数を書く。
- 2 人のプレイヤーはそれぞれ 1 つずつ駒を用意し、すぬけくんは自分の駒をマス 1 に、りんごさんは自分の駒をマス 2 に置く。
- 自分の駒が相手の駒より左にあるプレイヤーが駒を動かす。駒を動かす先は、今自分の駒が置かれているマスよりも右にあってかつ相手の駒が置かれていないマスでなければならない。
- 3. を繰り返し、これ以上駒を動かすことができなくなるとゲームは終了となる。
- ゲーム終了時までに自分の駒を置いたことのあるマスに書かれた整数の合計が、それぞれのプレイヤーのスコアとなる。
すぬけくんはすでにマス i (1≦i≦N-1) に整数 A_i を書きましたが、まだマス N には整数を書いていません。 すぬけくんは M 個の整数 X_1,X_2,...,X_M それぞれについて、その数をマス N に書いてゲームを行ったときに「(すぬけくんのスコア)ー(りんごさんのスコア)」がいくらになるのかを計算することにしました。 ただし、それぞれのプレイヤーは「(自分のスコア)ー(相手のスコア)」を最大化するように駒を動かすものとします。
制約
- 3≦N≦200,000
- 0≦A_i≦10^6
- A_i の総和は 10^6 以下である。
- 1≦M≦200,000
- 0≦X_i≦10^9
部分点
- M=1 を満たすデータセットに正解した場合は、700 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 900 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N
A_1 A_2 ... A_{N-1}
M
X_1
X_2
:
X_M
出力
X_1 \dots X_M の M 個の整数それぞれに対し、その数をマス N に書いたときの「(すぬけくんのスコア)ー(りんごさんのスコア)」を 1 行にひとつずつ出力せよ。
入力例 1
5 2 7 1 8 1 2
出力例 1
0
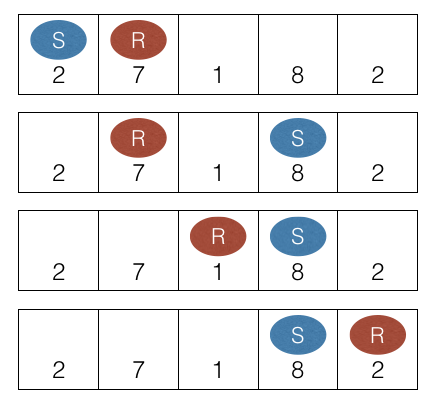
ゲームは下図のように進行します。Sはすぬけくんの駒、Rはりんごさんの駒を表しています。
スコアは 2 人とも 10 となり、「(すぬけくんのスコア)ー(りんごさんのスコア)」は 0 となります。
入力例 2
9 2 0 1 6 1 1 2 6 5 2016 1 1 2 6
出力例 2
2001 6 6 7 7
Score : 1600 points
Problem Statement
There are N squares in a row, numbered 1 through N from left to right. Snuke and Rng are playing a board game using these squares, described below:
- First, Snuke writes an integer into each square.
- Each of the two players possesses one piece. Snuke places his piece onto square 1, and Rng places his onto square 2.
- The player whose piece is to the left of the opponent's, moves his piece. The destination must be a square to the right of the square where the piece is currently placed, and must not be a square where the opponent's piece is placed.
- Repeat step 3. When the pieces cannot be moved any more, the game ends.
- The score of each player is calculated as the sum of the integers written in the squares where the player has placed his piece before the end of the game.
Snuke has already written an integer A_i into square i (1≦i≦N-1), but not into square N yet. He has decided to calculate for each of M integers X_1,X_2,...,X_M, if he writes it into square N and the game is played, what the value "(Snuke's score) - (Rng's score)" will be. Here, it is assumed that each player moves his piece to maximize the value "(the player's score) - (the opponent's score)".
Constraints
- 3≦N≦200,000
- 0≦A_i≦10^6
- The sum of all A_i is at most 10^6.
- 1≦M≦200,000
- 0≦X_i≦10^9
Partial Scores
- 700 points will be awarded for passing the test set satisfying M=1.
- Additional 900 points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_{N-1}
M
X_1
X_2
:
X_M
Output
For each of the M integers X_1, ..., X_M, print the value "(Snuke's score) - (Rng's score)" if it is written into square N, one per line.
Sample Input 1
5 2 7 1 8 1 2
Sample Output 1
0
The game proceeds as follows, where S represents Snuke's piece, and R represents Rng's.

Both player scores 10, thus "(Snuke's score) - (Rng's score)" is 0.
Sample Input 2
9 2 0 1 6 1 1 2 6 5 2016 1 1 2 6
Sample Output 2
2001 6 6 7 7
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 1900 点
問題文
縦 H 行、横 W 列のマス目があり、i 行目の j 列目のマスには文字 S_{i,j} が書かれています。
すぬけくんはこのマス目に対して以下の 2 種類の操作を行うことが出来ます。
- 行リバース:行を 1 つ選び、その行をリバースする。
- 列リバース:列を 1 つ選び、その列をリバースする。
例えば、2 行目をリバースした後に 4 列目をリバースすると以下のように変化します。

上記の操作を好きな順番で何回か行うことによって作ることの出来る文字の配置は何通り考えられるでしょうか?
制約
- 1≦H,W≦200
- S_{i,j} は小文字アルファベット(
a-z)である。
入力
入力は以下の形式で標準入力から与えられる。
H W
S_{1,1}S_{1,2}...S_{1,W}
S_{2,1}S_{2,2}...S_{2,W}
:
S_{H,1}S_{H,2}...S_{H,W}
出力
答えを 1000000007 (=10^9+7) で割ったあまりを出力せよ。
入力例 1
2 2 cf cf
出力例 1
6
以下の 6 通りの配置が考えられます。

入力例 2
1 12 codefestival
出力例 2
2
Score : 1900 points
Problem Statement
Snuke has a grid with H rows and W columns. The square at the i-th row and j-th column contains a character S_{i,j}.
He can perform the following two kinds of operation on the grid:
- Row-reverse: Reverse the order of the squares in a selected row.
- Column-reverse: Reverse the order of the squares in a selected column.
For example, reversing the 2-nd row followed by reversing the 4-th column will result as follows:

By performing these operations any number of times in any order, how many placements of characters on the grid can be obtained?
Constraints
- 1≦H,W≦200
- S_{i,j} is a lowercase English letter (
a-z).
Input
The input is given from Standard Input in the following format:
H W
S_{1,1}S_{1,2}...S_{1,W}
S_{2,1}S_{2,2}...S_{2,W}
:
S_{H,1}S_{H,2}...S_{H,W}
Output
Print the number of placements of characters on the grid that can be obtained, modulo 1000000007 (=10^9+7).
Sample Input 1
2 2 cf cf
Sample Output 1
6
The following 6 placements of characters can be obtained:

Sample Input 2
1 12 codefestival
Sample Output 2
2
実行時間制限: 4 sec / メモリ制限: 256 MiB
配点 : 2100 点
問題文
縦 N 行、横 N 列のマス目が書かれたボードと N \times N 枚のタイルがあります。
外側に面したマスの辺には、タイルの差込口がついています。 つまり、ボードの上下左右の辺にはそれぞれ N 個の差込口がついており、合計で 4 \times N 個の差込口があることになります。 それぞれの差込口には以下のように番号が付けられています。
- 上辺の差込口:左から順に U1, U2, ..., UN
- 下辺の差込口:左から順に D1, D2, ..., DN
- 左辺の差込口:上から順に L1, L2, ..., LN
- 右辺の差込口:上から順に R1, R2, ..., RN
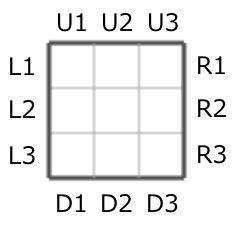
各差込口からはタイルを差し込むことが出来ます。 タイルが差し込まれたマスにすでにタイルが置かれていた場合は、置かれていたタイルは 1 つ先のマスに押し出され、さらにその 1 つ先のマスにタイルが置かれていた場合も同様に押し出されていきます。 ただし、押し出されたタイルがボードの外に出てしまう場合はタイルを差し込むことができません。 タイルを差し込んだときの挙動に関する詳しい例については入出力例 1 を参考にしてください。
すぬけくんは、N \times N 枚のタイルを 1 枚ずつ差込口から差し込むことによって、各マスに 1 枚ずつタイルが置かれている状態にしようとしています。 ただし、差込口 Ui からはちょうど U_i 枚、差込口 Di からはちょうど D_i 枚、差込口 Li からはちょうど L_i 枚、差込口 Ri からはちょうど R_i 枚のタイルを差し込まなければなりません。 このような差し込み方が可能かどうかを判定してください。また、可能な場合は差し込む順番を出力してください。
制約
- 1≦N≦300
- U_i,D_i,L_i,R_i は 0 以上の整数である。
- U_i,D_i,L_i,R_i の和は N \times N と等しい。
部分点
- N≦40 を満たすデータセットに正解した場合は、2000 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 100 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N U_1 U_2 ... U_N D_1 D_2 ... D_N L_1 L_2 ... L_N R_1 R_2 ... R_N
出力
各マスに 1 枚ずつタイルが置かれるようにタイルを差し込むことが可能ならば、差込口の番号を差し込むべき順番で 1 行にひとつずつ出力せよ。不可能な場合は、代わりに NO と出力せよ。また、差し込む順番が複数考えられる場合は、そのうちの 1 つを出力すれば良い。
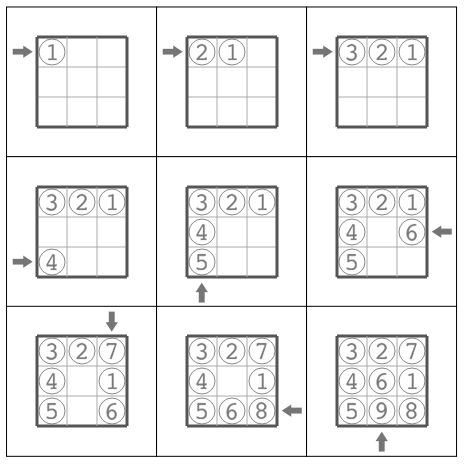
入力例 1
3 0 0 1 1 1 0 3 0 1 0 1 1
出力例 1
L1 L1 L1 L3 D1 R2 U3 R3 D2
下図の通りに差し込めば良いです。矢印は差し込む場所を、丸はタイルを、丸の中に書かれた番号はそのタイルが何番目に差し込まれたかを表しています。
入力例 2
2 2 0 2 0 0 0 0 0
出力例 2
NO
Score : 2100 points
Problem Statement
Snuke has a board with an N \times N grid, and N \times N tiles.
Each side of a square that is part of the perimeter of the grid is attached with a socket. That is, each side of the grid is attached with N sockets, for the total of 4 \times N sockets. These sockets are labeled as follows:
- The sockets on the top side of the grid: U1, U2, ..., UN from left to right
- The sockets on the bottom side of the grid: D1, D2, ..., DN from left to right
- The sockets on the left side of the grid: L1, L2, ..., LN from top to bottom
- The sockets on the right side of the grid: R1, R2, ..., RN from top to bottom

Snuke can insert a tile from each socket into the square on which the socket is attached. When the square is already occupied by a tile, the occupying tile will be pushed into the next square, and when the next square is also occupied by another tile, that another occupying tile will be pushed as well, and so forth. Snuke cannot insert a tile if it would result in a tile pushed out of the grid. The behavior of tiles when a tile is inserted is demonstrated in detail at Sample Input/Output 1.
Snuke is trying to insert the N \times N tiles one by one from the sockets, to reach the state where every square contains a tile. Here, he must insert exactly U_i tiles from socket Ui, D_i tiles from socket Di, L_i tiles from socket Li and R_i tiles from socket Ri. Determine whether it is possible to insert the tiles under the restriction. If it is possible, in what order the tiles should be inserted from the sockets?
Constraints
- 1≦N≦300
- U_i,D_i,L_i and R_i are non-negative integers.
- The sum of all values U_i,D_i,L_i and R_i is equal to N \times N.
Partial Scores
- 2000 points will be awarded for passing the test set satisfying N≦40.
- Additional 100 points will be awarded for passing the test set without additional constraints.
Input
The input is given from Standard Input in the following format:
N U_1 U_2 ... U_N D_1 D_2 ... D_N L_1 L_2 ... L_N R_1 R_2 ... R_N
Output
If it is possible to insert the tiles so that every square will contain a tile, print the labels of the sockets in the order the tiles should be inserted from them, one per line. If it is impossible, print NO instead. If there exists more than one solution, print any of those.
Sample Input 1
3 0 0 1 1 1 0 3 0 1 0 1 1
Sample Output 1
L1 L1 L1 L3 D1 R2 U3 R3 D2
Snuke can insert the tiles as shown in the figure below. An arrow indicates where a tile is inserted from, a circle represents a tile, and a number written in a circle indicates how many tiles are inserted before and including the tile.

Sample Input 2
2 2 0 2 0 0 0 0 0
Sample Output 2
NO