実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
H\times W のマス目があります.上から h 行目,左から w 列目のマスを (h,w) で表します.さらに,D, R, ? からなる長さ H+W-2 の文字列 S=S_1\cdots S_{H+W-2} が与えられます.
はじめ,すべてのマスは白色で塗られています.あなたは次の 3 つの手順からなる操作を何度でも行うことができます:
- 以下の条件をすべて満たす長さ H+W-2 の文字列 X=X_1\cdots X_{H+W-2} をひとつ選ぶ.
- X は H-1 個の
Dおよび W-1 個のRからなる. - 1\leq i\leq H+W-2 に対して,S_i が
Dならば X_i もDである. - 1\leq i\leq H+W-2 に対して,S_i が
Rならば X_i もRである.
- X は H-1 個の
- マス (1,1) に立つ.さらに i=1,2,\ldots の順に,文字 X_i の表す方向に 1 マス移動する.つまり,X_i が
Dならば下方向,X_i がRならば右方向に 1 マス移動する.なお,X が手順 1 の条件を満たすとき,移動先のマスは必ずマス目内に存在することが証明できる. - 手順 2 においてあなたが通ったすべてのマス(最初・最後のマスも含む)について,そのマスが白色で塗られているならば,黒色で塗る.
最終的に黒色で塗ることができるマスの個数としてありうる最大値を求めてください.
T 個のテストケースが与えられるので,それぞれについて解いてください.
制約
- 1\leq T\leq 2\times 10^5
- 2\leq H, W\leq 2\times 10^5
- T,H,W は整数.
- S は
D,R,?からなる長さ H+W-2 の文字列. - S に含まれる
Dの個数は H-1 以下. - S に含まれる
Rの個数は W-1 以下. - すべてのテストケースにわたる H+W の総和は 4\times 10^5 以下.
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
H W S
出力
T 行出力してください.i 行目には i 番目のテストケースについて,最終的に黒色で塗ることができるマスの個数としてありうる最大値を出力してください.
入力例 1
4 4 5 D?DRR?R 4 5 DDRRDRR 4 5 ??????? 2 2 DR
出力例 1
12 8 20 3
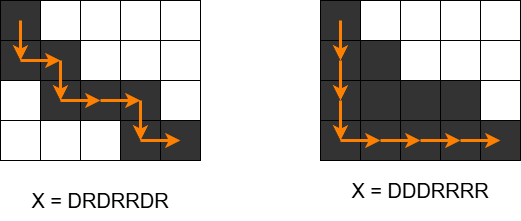
1 つめのテストケースについて,1 回目に X として DRDRRDR を選び,2 回目に X として DDDRRRR を選ぶことで,12 個のマスを黒く塗ることができます.
Score : 400 points
Problem Statement
There is an H\times W grid of cells. Let (h,w) denote the cell at the h-th row from the top and the w-th column from the left. Furthermore, you are given a string S = S_1\cdots S_{H+W-2} of length H+W-2 consisting of D, R, and ?.
Initially, all cells are painted white. You may perform the following operation, which consists of three steps, any number of times:
- Choose a string X = X_1\cdots X_{H+W-2} of length H+W-2 satisfying all of the following.
- X consists of exactly H-1
Ds and W-1Rs. - For each 1 \le i \le H+W-2, if S_i is
Dthen X_i must also beD. - For each 1 \le i \le H+W-2, if S_i is
Rthen X_i must also beR.
- X consists of exactly H-1
- Stand on cell (1,1). Then for i=1,2,\ldots in order, move one cell in the direction indicated by X_i: if X_i is
D, move down one cell; if X_i isR, move right one cell. It can be shown that if X satisfies the conditions in step 1, the destination cell always exists within the grid. - For every cell you visited in step 2 (including the starting and ending cells), if the cell is currently white, paint it black.
Find the maximum possible number of cells that can be painted black in total.
There are T test cases; solve each one.
Constraints
- 1\le T\le 2\times 10^5
- 2\le H,W\le 2\times 10^5
- T,H,W are integers.
- S is a string of length H+W-2 consisting of
D,R, and?. - The number of
Ds in S is at most H-1. - The number of
Rs in S is at most W-1. - The sum of H+W over all test cases is at most 4\times 10^5.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
H W S
Output
Print T lines. The i-th line should contain the maximum number of cells that can be painted black for the i-th test case.
Sample Input 1
4 4 5 D?DRR?R 4 5 DDRRDRR 4 5 ??????? 2 2 DR
Sample Output 1
12 8 20 3
For the first test case, by choosing X as DRDRRDR in the first operation and DDDRRRR in the second operation, you can paint 12 cells black.

実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
空でない整数列 x = (x_1, \ldots, x_n) のスコアを,x の要素のうちで x の平均値より大きなものの個数として定めます.
つまり,x のスコアは x_i > \dfrac{x_1+\cdots+x_n}{n} を満たす i の個数です.
長さ N の整数列 A=(A_1,\ldots,A_N) が与えられます. A の空でない部分列に対するスコアの最大値を求めてください.
T 個のテストケースが与えられるので,それぞれについて解いてください.
部分列とは
数列 A の部分列とは,A の要素を 0 個以上選んで削除し,残った要素を元の順序を保って並べた数列のことを指します.制約
- 1\leq T\leq 2\times 10^5
- 2\leq N\leq 2\times 10^5
- 1\leq A_i\leq 10^9
- 入力される値はすべて整数
- すべてのテストケースにわたる N の総和は 2\times 10^5 以下.
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
N A_1 \cdots A_N
出力
T 行出力してください.i 行目には i 番目のテストケースについて,A の空でない部分列に対するスコアの最大値を出力してください.
入力例 1
3 5 2 6 5 7 5 5 10 10 10 10 10 5 1 10 100 1000 10000
出力例 1
3 0 1
1 つめのテストケースについて,空でない部分列の平均値とスコアの例を以下に示します.
- x = (A_1) = (2):平均値は 2,スコアは 0 です.
- x = (A_3,A_5) = (5, 5):平均値は 5,スコアは 0 です.
- x = (A_1,A_3,A_4,A_5) = (2, 5, 7, 5):平均値は \dfrac{19}{4},スコアは 3 です.
- x = (A_1,A_2,A_3,A_4,A_5) = (2, 6, 5, 7, 5):平均値は 5,スコアは 2 です.
Score : 500 points
Problem Statement
Define the score of a non-empty integer sequence x = (x_1, \ldots, x_n) as the number of elements of x that are strictly greater than the average of x.
That is, the score of x is the count of indices i satisfying x_i > \dfrac{x_1+\cdots+x_n}{n}.
You are given a length-N integer sequence A = (A_1, \ldots, A_N). Find the maximum score of a non-empty subsequence of A.
There are T test cases; solve each one.
Definition of subsequence
A subsequence of A is any sequence obtained by deleting zero or more elements from A and keeping the remaining elements in their original order.Constraints
- 1\le T\le 2\times 10^5
- 2\le N\le 2\times 10^5
- 1\le A_i\le 10^9
- All input values are integers.
- The sum of N over all test cases is at most 2\times 10^5.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
N A_1 \cdots A_N
Output
Print T lines. The i-th line should contain the maximum score of a non-empty subsequence of A for the i-th test case.
Sample Input 1
3 5 2 6 5 7 5 5 10 10 10 10 10 5 1 10 100 1000 10000
Sample Output 1
3 0 1
For the first test case, below are examples of subsequences, their averages, and their scores.
- x = (A_1) = (2): the average is 2, and the score is 0.
- x = (A_3,A_5) = (5,5): the average is 5, and the score is 0.
- x = (A_1,A_3,A_4,A_5) = (2,5,7,5): the average is \frac{19}{4}, and the score is 3.
- x = (A_1,A_2,A_3,A_4,A_5) = (2,6,5,7,5): the average is 5, and the score is 2.
実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
すべての正整数からなる集合 S があります.
Q 個のクエリを順に処理してください.i 番目のクエリでは,2 以上の整数 A_i および,正整数 B_i が与えられるので,次の 2 つのことを順に行ってください.
- S から A_i の倍数である要素をすべて削除する.
- S の要素のうち小さい方から B_i 番目のものを出力する.なお本問の制約のもとで,S はこの時点で B_i 個以上の要素を含むことが証明できる.
制約
- 1\leq Q\leq 10^5
- 2\leq A_i\leq 10^9
- 1\leq B_i\leq 10^5
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられます.
Q A_1 B_1 \vdots A_Q B_Q
出力
Q 行出力してください.i 行目には i 番目のクエリにおいて,S から A_i の倍数である要素をすべて削除した後の,S の要素のうち小さい方から B_i 番目のものを出力してください.
入力例 1
5 5 10 6 1 6 10 9 10 123456789 111
出力例 1
12 1 14 16 178
S の要素を昇順に並べたときの先頭に近い部分がどうなるかを説明します.
- 初期状態では,S=\lbrace 1,2,3,4,5,6,7,8,9,10,\ldots\rbrace です.
- 1 番目のクエリでは 5 の倍数を削除して,S=\lbrace1,2,3,4,6,7,8,9,11,12,\ldots\rbrace となります.
- 2 番目のクエリでは 6 の倍数を削除して,S=\lbrace1,2,3,4,7,8,9,11,13,14,\ldots\rbrace となります.
- 3 番目のクエリでは 6 の倍数を削除して,S=\lbrace1,2,3,4,7,8,9,11,13,14,\ldots\rbrace となります.
- 4 番目のクエリでは 9 の倍数を削除して,S=\lbrace1,2,3,4,7,8,11,13,14,16,\ldots\rbrace となります.
- 5 番目のクエリでは 123456789 の倍数を削除して,S=\lbrace1,2,3,4,7,8,11,13,14,16,\ldots\rbrace となります.
Score : 600 points
Problem Statement
Let S be the set of all positive integers.
Process Q queries in order. The i-th query gives you an integer A_i not less than 2 and a positive integer B_i, so perform the following two steps in order.
- Remove from S all elements that are multiples of A_i.
- Print the B_i-th smallest element of S. It can be shown that under the given constraints, S contains at least B_i elements at this point.
Constraints
- 1\le Q\le 10^5
- 2\le A_i\le 10^9
- 1\le B_i\le 10^5
- All input values are integers.
Input
The input is given from Standard Input in the following format:
Q A_1 B_1 \vdots A_Q B_Q
Output
Print Q lines. The i-th line should contain the B_i-th smallest element of S after removing all multiples of A_i from S.
Sample Input 1
5 5 10 6 1 6 10 9 10 123456789 111
Sample Output 1
12 1 14 16 178
When the elements of S are listed in ascending order, the beginning of the list evolves as follows.
- Initially, S=\lbrace 1,2,3,4,5,6,7,8,9,10,\ldots\rbrace.
- The first query removes multiples of 5, resulting in S=\lbrace1,2,3,4,6,7,8,9,11,12,\ldots\rbrace.
- The second query removes multiples of 6, resulting in S=\lbrace1,2,3,4,7,8,9,11,13,14,\ldots\rbrace.
- The third query removes multiples of 6, resulting in S=\lbrace1,2,3,4,7,8,9,11,13,14,\ldots\rbrace.
- The fourth query removes multiples of 9, resulting in S=\lbrace1,2,3,4,7,8,11,13,14,16,\ldots\rbrace.
- The fifth query removes multiples of 123456789, resulting in S=\lbrace1,2,3,4,7,8,11,13,14,16,\ldots\rbrace.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
N\times N 行列 A = (A_{i,j}) (1\leq i,j\leq N) が与えられます.A の成分は 0 または 1 です.
頂点に 1 から N までの番号が付けられた N 頂点の木 G であって,次の条件を満たすものの個数を 998244353 で割った余りを求めてください.
- A_{i,j}=1 であることと,以下の 2 条件のうち少なくともひとつが成り立つことは同値である:
- 頂点 1 を根としたとき頂点 j は頂点 i の祖先である.つまり頂点 j は,頂点 1, i を結ぶ G 上のパス上にある.
- 頂点 1 を根としたとき頂点 i は頂点 j の祖先である.つまり頂点 i は,頂点 1, j を結ぶ G 上のパス上にある.
ただし,パスの端点もパス上にあると見なします.G は木であるとき,2 頂点を結ぶ G 上のパスは一意に存在することにも注意してください.
T 個のテストケースが与えられるので,それぞれについて解いてください.
制約
- 1\leq T\leq 10^5
- 2\leq N\leq 400
- A_{i,j}\in \lbrace 0,1\rbrace (1\leq i,j\leq N)
- A_{i,i}=1 (1\leq i\leq N)
- A_{i,j}=A_{j,i} (1\leq i,j\leq N)
- すべてのテストケースにわたる N^2 の総和は 400^2 以下.
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
N
A_{1,1} \cdots A_{1,N}
\vdots
A_{N,1} \cdots A_{N,N}
出力
T 行出力してください.i 行目には i 番目のテストケースについて,条件を満たす N 頂点の木 G の個数を 998244353 で割った余りを出力してください.
入力例 1
5 3 1 1 1 1 1 0 1 0 1 3 1 1 1 1 1 1 1 1 1 3 1 0 0 0 1 0 0 0 1 3 1 0 1 0 1 1 1 1 1 7 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 1 1
出力例 1
1 2 0 0 8
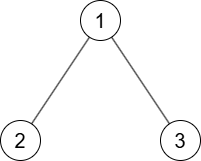
1 番目のテストケースでは次の 1 つの G が条件を満たします.
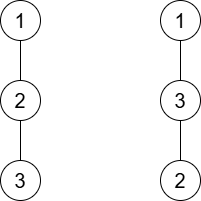
2 番目のテストケースでは次の 2 つの G が条件を満たします.
Score : 700 points
Problem Statement
You are given an N\times N matrix A = (A_{i,j}) (1\le i,j\le N) whose entries are 0 or 1.
Find, modulo 998244353, the number of trees G on N vertices numbered 1 to N that satisfy the following condition.
- A_{i,j}=1 if and only if at least one of the following holds:
- When G is rooted at vertex 1, Vertex j is an ancestor of vertex i. That is, vertex j lies on the unique path in G between vertices 1 and i.
- When G is rooted at vertex 1, Vertex i is an ancestor of vertex j. That is, vertex i lies on the unique path in G between vertices 1 and j.
Here, the endpoints of a path are considered to be on that path. Note that G being a tree guarantees uniqueness of the path between any two vertices.
There are T test cases; solve each one.
Constraints
- 1\leq T\leq 10^5
- 2\leq N\leq 400
- A_{i,j}\in \lbrace 0,1\rbrace (1\leq i,j\leq N)
- A_{i,i}=1 (1\leq i\leq N)
- A_{i,j}=A_{j,i} (1\leq i,j\leq N)
- The sum of N^2 over all test cases is at most 400^2.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
N
A_{1,1} \cdots A_{1,N}
\vdots
A_{N,1} \cdots A_{N,N}
Output
Print T lines. The i-th line should contain the number, modulo 998244353, of trees G satisfying the conditions for the i-th test case.
Sample Input 1
5 3 1 1 1 1 1 0 1 0 1 3 1 1 1 1 1 1 1 1 1 3 1 0 0 0 1 0 0 0 1 3 1 0 1 0 1 1 1 1 1 7 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 1 1
Sample Output 1
1 2 0 0 8
In the first test case, the following one tree G satisfies the condition:

In the second test case, the following two trees G satisfy the condition:

実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 800 点
問題文
正整数 N, H, W が与えられます.ただし,H, W \leq 3N-1 が成り立ちます.
H\times W のマス目に N\times N の正方形のタイルを 4 個置く方法であって,以下の条件をすべて満たすものの個数を 998244353 で割った余りを求めてください.
- 各タイルは,マス目の ちょうど N^2 個のマスを完全に覆う.
- ひとつのマスが複数のタイルによって覆われてはならない.
ただし,タイル同士は区別しません.
T 個のテストケースが与えられるので,それぞれについて解いてください.
制約
- 1\leq T\leq 2\times 10^5
- 1\leq N,H,W\leq 10^9
- H,W\leq 3N - 1
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
N H W
出力
T 行出力してください.i 行目には i 番目のテストケースについて,条件を満たすようにタイルを置く方法の個数を 998244353 で割った余りを出力してください.
入力例 1
4 2 4 5 2 5 5 1000 1000 1000 1000 2222 2025
出力例 1
9 79 0 262210557
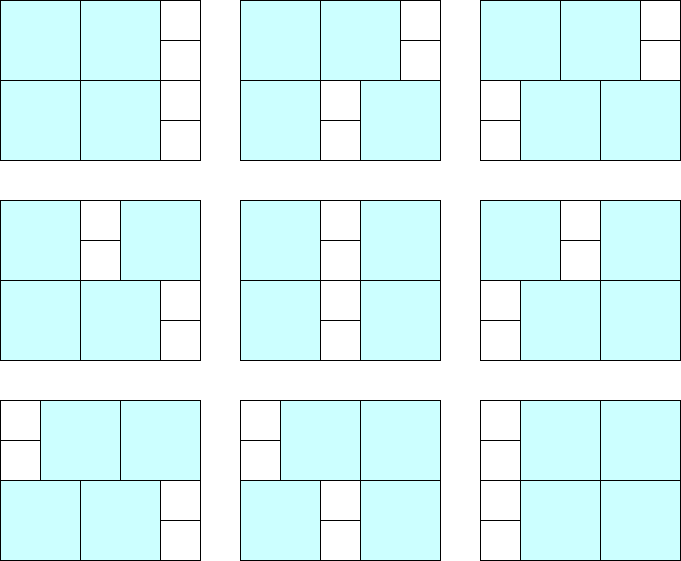
1 つめのテストケースについて,次の図で示す 9 通りの方法があります.
Score : 800 points
Problem Statement
You are given positive integers N, H, and W, with H,W \le 3N-1.
Find the number, modulo 998244353, of ways to place four N\times N square tiles on an H\times W grid that satisfy all of the following conditions.
- Each tile exactly covers N^2 cells of the grid.
- No cell is covered by more than one tile.
Here, the tiles are indistinguishable.
There are T test cases; solve each one.
Constraints
- 1\le T\le 2\times 10^5
- 1\le N,H,W\le 10^9
- H,W\le 3N-1
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
N H W
Output
Print T lines. The i-th line should contain the number, modulo 998244353, of valid ways to place the tiles for the i-th test case.
Sample Input 1
4 2 4 5 2 5 5 1000 1000 1000 1000 2222 2025
Sample Output 1
9 79 0 262210557
For the first test case, there are 9 ways as illustrated in the following figure:
