実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
長さ N の数列 A = (A_1, A_2, \ldots, A_N) が与えられます。
あなたはこの数列の隣接する 2 数を選びどちらもこの数列から削除する、という操作を数列の長さが 1 以下になるまで繰り返します。
一度の操作で得られるスコアは選んだ 2 数の差の絶対値です。
得られるスコアの合計としてありうる最大値を求めてください。
制約
- 2 \le N \le 3 \times 10^5
- 1 \le A_i \le 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
得られるスコアの合計としてありうる最大値を出力せよ。
入力例 1
4 1 2 5 3
出力例 1
5
まず、A_2 と A_3 を削除します。このとき得られるスコアは |A_2-A_3|=3 です。
次に、A_1 と A_4 を削除します。前回の操作の影響で、この 2 数は隣接しているということに注意してください。このとき得られるスコアは |A_1-A_4|=2 です。
よって、得られるスコアの合計は 5 となります。
6 以上の合計スコアを達成することはできないので、5 を出力します。
入力例 2
7 3 1 4 1 5 9 2
出力例 2
14
入力例 3
5 1 1 1 1 1
出力例 3
0
Score : 700 points
Problem Statement
You are given a length-N sequence A = (A_1, A_2, \ldots, A_N).
You will repeatedly perform the following operation until the sequence has length at most 1: choose two adjacent numbers and remove both from the sequence.
The score obtained in one operation is the absolute difference of the two chosen numbers.
Find the maximum possible total score obtained.
Constraints
- 2 \le N \le 3 \times 10^5
- 1 \le A_i \le 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Print the maximum possible total score obtained.
Sample Input 1
4 1 2 5 3
Sample Output 1
5
First, remove A_2 and A_3. The score obtained is |A_2 - A_3| = 3.
Next, remove A_1 and A_4. Note that, because of the previous operation, these two numbers are now adjacent. The score obtained is |A_1 - A_4| = 2.
Hence, the total score obtained is 5.
It is impossible to achieve a total score of 6 or greater, so print 5.
Sample Input 2
7 3 1 4 1 5 9 2
Sample Output 2
14
Sample Input 3
5 1 1 1 1 1
Sample Output 3
0
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
H 行 W 列のグリッドがあります。 行には上から順に 0,1,\ldots, H-1 の番号が、列には左から順に 0,1,\ldots,W-1 の番号がついています。 行 i、列 j のマスをマス (i,j) と表すことにします。
H 個の文字列 S_0, S_1, \ldots, S_{H-1} が与えられます。それぞれの文字列は A と B のみからなる長さ W の文字列です。
各マスには、以下の 2 種類のタイルのいずれかを配置します。S_i の j+1 文字目 (0\leq j \leq W-1) を S_{ij} としたとき、マス (i,j) に配置するタイルの種類は S_{ij} です。
- 種類 A:タイルの表面に、隣接する 2 辺の中点どうしを結ぶ線分が一本描かれている

- 種類 B:タイルの表面に、向かい合う 2 辺の中点どうしを結ぶ線分が一本描かれている

タイルは自由に回転可能です。タイルの表面に描かれた線分のみに注目したとき、種類 A のタイルを回転する方法は 4 通り、種類 B のタイルを回転する方法は 2 通りあります。よって、線分が作る模様のみによってタイルの配置方法を区別したとき、タイルを配置する方法の数は、種類 A のタイルの数 a、種類 B のタイルの数 b を用いて、 4^a\times 2^b 通りと表されます。
このうち、グリッドをトーラスとして見たときにタイルに描かれた線分が行き止まりを持たないようにタイルを配置する方法の数を 998244353 で割ったあまりを出力してください。
ここで、グリッドをトーラスとして見たときにタイルに描かれた線分が行き止まりを持たないとは、具体的には、すべてのマス (i,j) について以下の 2 条件をともに満たすことを言います。
- 次の 2 つが、両方とも存在する、あるいはどちらも存在しない。
- マス (i,j) のタイルの右辺の中点を端点とする、マス (i,j) のタイルの表面に描かれた線分
- マス (i,(j+1)\bmod W) のタイルの左辺の中点を端点とする、マス (i,(j+1)\bmod W) のタイルの表面に描かれた線分
- 次の 2 つが、両方とも存在する、あるいはどちらも存在しない。
- マス (i,j) のタイルの下辺の中点を端点とする、マス (i,j) のタイルの表面に描かれた線分
- マス ((i+1)\bmod H,j) のタイルの上辺の中点を端点とする、マス ((i+1)\bmod H,j) のタイルの表面に描かれた線分
例えば、次の配置方法は条件を満たします。
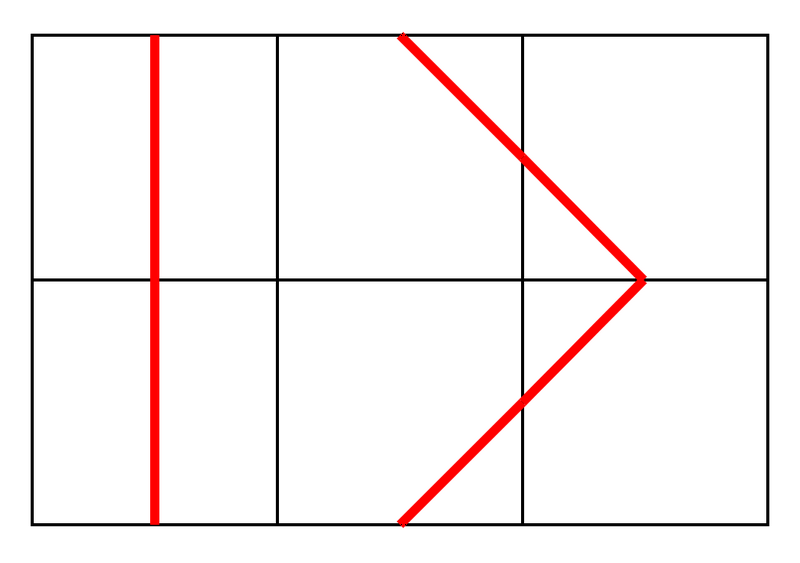
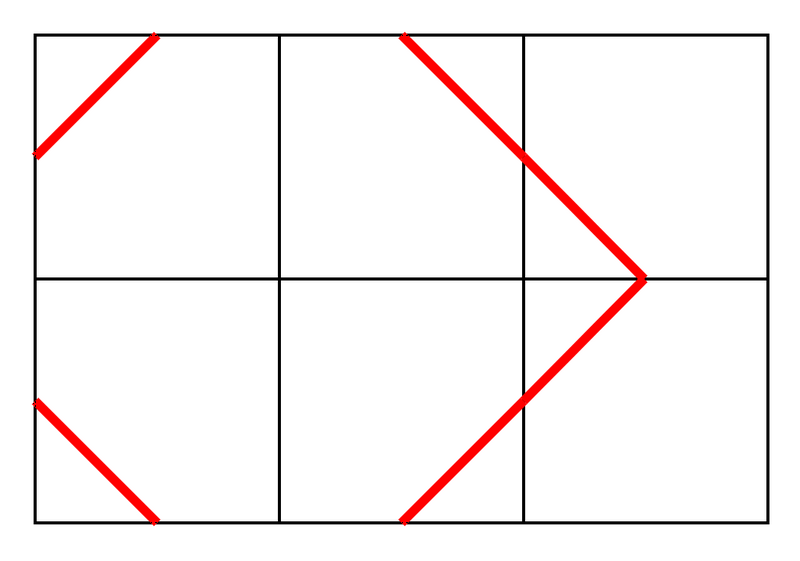
次の配置方法は条件を満たしません。具体的には、マス (0,2) のタイルの右辺の中点を端点とする線分が存在しないのに対し、マス (0,0) のタイルの左辺の中点を端点とする線分は存在するので、条件を満たしません。
T 個のテストケースが与えられるので、それぞれについて解いてください。
制約
- 1 \le T \le 10^5
- 2 \le H,W
- HW\leq 10^6
- S_i\,(0\le i\le H-1) は
AとBのみからなる長さ W の文字列 - すべてのテストケースにわたる HW の総和は 10^6 以下
- T, H, W は整数
入力
入力は以下の形式で標準入力から与えられる。
T case_1 case_2 \vdots case_T
各ケースは以下の形式で与えられる。
H W
S_0
S_1
\vdots
S_{H-1}
出力
各テストケースに対する、問題文中の条件を満たすタイルの配置方法の数を 998244353 で割ったあまりを改行区切りで出力せよ。
入力例 1
3 3 3 AAB AAB BBB 3 3 BBA ABA AAB 3 4 BAAB BABA BBAA
出力例 1
2 0 2
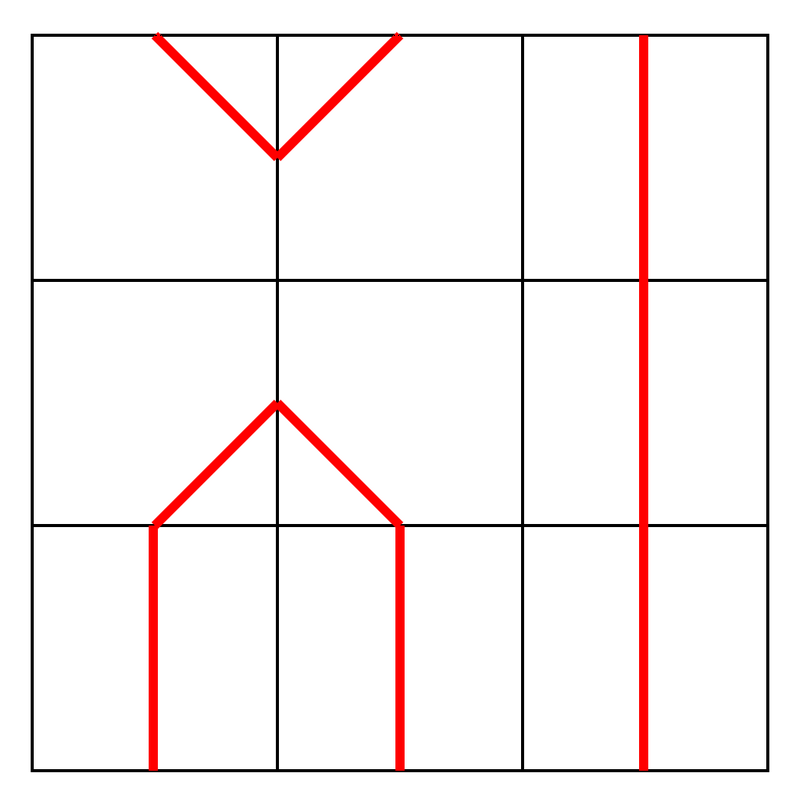
1 番目のテストケースにおける正しい配置の一つの例として、以下の画像のようにタイルを配置する方法があります。
Score : 700 points
Problem Statement
There is a grid of H rows and W columns. The rows are numbered 0,1,\ldots,H-1 from top to bottom, and the columns are numbered 0,1,\ldots,W-1 from left to right. Let (i,j) denote the cell at row i and column j.
You are given H strings S_0, S_1, \ldots, S_{H-1}, each of which is of length W and consists of A and B.
In each cell, one of the following two types of tiles is placed. Let S_{ij} denote the (j+1)-th character (0 \le j \le W-1) of the string S_i. The type of tile placed in cell (i,j) is S_{ij}.
- Type A: A single line segment is drawn on the tile’s surface, connecting the midpoints of two adjacent edges.

- Type B: A single line segment is drawn on the tile’s surface, connecting the midpoints of two opposite edges.

These tiles can be freely rotated. When focusing only on the pattern formed by the line segments, there are four ways to rotate a Type-A tile and two ways to rotate a Type-B tile. Therefore, if we distinguish placements only by the pattern of line segments, the number of ways to place the tiles is 4^a \times 2^b, where a is the number of Type-A tiles and b is the number of Type-B tiles.
Among these ways, print the number, modulo 998244353, of ways such that the line segments on the tiles have no dead ends when viewing the grid as a torus.
Here, "the line segments on the tiles have no dead ends when viewing the grid as a torus" if and only if the following two conditions are satisfied for every cell (i,j):
- Both of the following exist, or neither of the following exists:
- the line segment drawn in the cell (i,j), whose endpoint is the midpoint of the right edge of the cell (i,j)
- the line segment drawn in the cell (i,(j+1)\bmod W), whose endpoint is the midpoint of the left edge of the cell (i,(j+1)\bmod W)
- Both of the following exist, or neither of the following exists:
- the line segment drawn in the cell (i,j), whose endpoint is the midpoint of the bottom edge of the cell (i,j)
- the line segment drawn in the cell ((i+1)\bmod H,j), whose endpoint is the midpoint of the top edge of the cell ((i+1)\bmod H,j)
For example, the following placement satisfies the condition:

The following placement does not satisfy the condition. Specifically, while there is no line segment whose endpoint is the midpoint of the right edge of the tile in cell (0,2), there is a line segment whose endpoint is the midpoint of the left edge of the tile in cell (0,0), so the condition is not satisfied.

You are given T test cases; solve each of them.
Constraints
- 1 \le T \le 10^5
- 2 \le H,W
- HW\leq 10^6
- S_i\,(0\le i\le H-1) are length-W strings consisting of
AandB. - The sum of H W over all test cases is at most 10^6.
- T, H, and W are integers.
Input
The input is given from Standard Input in the following format:
T case_1 case_2 \vdots case_T
Each case is given in the following format:
H W
S_0
S_1
\vdots
S_{H-1}
Output
For each test case, print the number, modulo 998244353, of placements that satisfies the condition, in separate lines.
Sample Input 1
3 3 3 AAB AAB BBB 3 3 BBA ABA AAB 3 4 BAAB BABA BBAA
Sample Output 1
2 0 2
One valid placement for the first test case is shown in the following image:

実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 900 点
問題文
2N 頂点 2N-1 辺の有向グラフがあります。 頂点には 1, 2, \ldots, 2N の番号がついており、i 番目の辺は頂点 i から頂点 i+1 に向かう有向辺です。
N 個の W と N 個の B からなる長さ 2N の文字列 S=S_1S_2\ldots S_{2N} が与えられます。
頂点 i は S_i が W のとき白、B のとき黒で塗られています。
あなたは以下の一連の操作を行います。
- 2N 個の頂点を白の頂点と黒の頂点 1 つずつからなる N 組のペアに分ける。
- 各ペアについて白の頂点から黒の頂点に向かう辺を追加する。
操作において頂点を N 組のペアに分ける方法のうち、最終的に得られるグラフが強連結となるような方法の数を 998244353 で割ったあまりを出力してください。
強連結とは?
有向グラフが強連結であるとは、グラフに含まれる任意の頂点から任意の頂点にいくつかの辺をたどって移動可能であることを言います。
制約
- 1 \le N \le 2\times 10^5
- S は N 個の
Wと N 個のBからなる長さ 2N の文字列 - N は整数
入力
入力は以下の形式で標準入力から与えられる。
N S
出力
操作において頂点を N 組のペアに分ける方法のうち、最終的に得られるグラフが強連結となるような方法の数を 998244353 で割ったあまりを出力せよ。
入力例 1
2 BWBW
出力例 1
1
頂点 2,4 は白色で、頂点 1,3 は黒色で塗られています。
頂点 u から頂点 v を向かう辺を辺 (u,v) で表すことにします。
頂点 (2,1), (4,3) のようにペア分けをした場合、最終的なグラフに存在する辺は辺 (1,2), (2,3), (3,4), (2,1), (4,3) となります。このとき、例えば頂点 3 から頂点 1 にいくつかの辺をたどって移動することはできないので、このグラフは強連結ではありません。
頂点 (2,3), (4,1) のようにペア分けをした場合、最終的なグラフに存在する辺は,(1,2), (2,3), (3,4), (2,3), (4,1) となります。このグラフは強連結です。
よって条件を満たすペア分けの方法の数は 1 通りです。
入力例 2
4 BWWBWBWB
出力例 2
0
どのようにペア分けを行っても条件を満たすことができません。
入力例 3
9 BWWBWBBBWWBWBBWWBW
出力例 3
240792
Score : 900 points
Problem Statement
There is a directed graph with 2N vertices and 2N-1 edges. The vertices are numbered 1, 2, \ldots, 2N, and the i-th edge is a directed edge from vertex i to vertex i+1.
You are given a length-2N string S = S_1 S_2 \ldots S_{2N} consisting of N Ws and N Bs.
Vertex i is colored white if S_i is W, and black if S_i is B.
You will perform the following series of operations:
- Partition the 2N vertices into N pairs, each consisting of one white vertex and one black vertex.
- For each pair, add a directed edge from the white vertex to the black vertex.
Print the number, modulo 998244353, of ways to partition the vertices into N pairs such that the final graph is strongly connected.
Notes on strongly connectedness
A directed graph is strongly connected if and only if it is possible to travel from any vertex to any vertex by following edges.
Constraints
- 1 \le N \le 2\times 10^5
- S is a length 2N string consisting of N
Ws and NBs. - N is an integer.
Input
The input is given from Standard Input in the following format:
N S
Output
Print the number, modulo 998244353, of ways to partition the vertices into N pairs so that the final graph is strongly connected.
Sample Input 1
2 BWBW
Sample Output 1
1
Vertices 2,4 are white, and vertices 1,3 are black.
Let (u,v) denote an edge from vertex u to vertex v.
If we pair up vertices as (2,1), (4,3), the final graph have the edges (1,2), (2,3), (3,4), (2,1), (4,3). In this case, for example, it is impossible to travel from vertex 3 to vertex 1 by following edges, so this graph is not strongly connected.
If we pair up vertices as (2,3), (4,1), the final graph have the edges (1,2), (2,3), (3,4), (2,3), (4,1). This graph is strongly connected.
Therefore, there is exactly 1 way to pair up the vertices that satisfies the condition.
Sample Input 2
4 BWWBWBWB
Sample Output 2
0
No matter how you pair up the vertices, you cannot satisfy the condition.
Sample Input 3
9 BWWBWBBBWWBWBBWWBW
Sample Output 3
240792
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 900 点
問題文
町 1,2, \ldots, N の N 個の町がこの順に一列に並んでいます。
また、隣り合う町どうしを結ぶ N-1 本の道があり、道 j\,(1\leq j \leq N-1) は町 j と町 j+1 を結んでいます。あなたは各道 j について、強さ w_j(非負とは限らない整数)を設定することができます。
人が道を通るとその人の体力が変化します。具体的には、体力が x の人が道 j を通ると、体力が x+w_j に変化します。
M 人の人がこれから町の間を移動します。
人 i\,(1\le i\le M) は体力 0 の状態で町 S_i を出発し、最短経路で町 T_i に向かいます。 ここで、|S_i-T_i|>1 が保証されます。また、i\neq j ならば (S_i, T_i) \neq (S_j, T_j) です。
人 i の要求は以下です。
町 S_i を出発する時と町 T_i に到着する時は体力がちょうど 0 で、それ以外の町にいる時は常に体力が正整数であってほしい。
ただし、上記で説明された、道を通ることによる影響以外での体力の増減はないものとします。
Q 個のクエリを処理してください。k\,(1\le k\le Q) 番目のクエリでは、人 L_k, L_k + 1, \ldots , R_k の要求を全て満たすように道の強さを設定する方法がある場合 Yes を、ない場合 No を出力してください。
制約
- 3 \le N \le 4 \times 10^5
- 1 \le M \le 2 \times 10^5
- 1 \le Q \le 2 \times 10^5
- 1 \le S_i, T_i \le N
- |S_i-T_i|>1
- (S_i, T_i) \neq (S_j, T_j)\,(i\neq j)
- 1\le L_k\le R_k \le M
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M Q S_1 T_1 S_2 T_2 \vdots S_M T_M L_1 R_1 L_2 R_2 \vdots L_Q R_Q
出力
Q 行出力せよ。
k 行目には、人 L_k, L_k + 1, \ldots , R_k の要求を全て満たすように道の強さを設定する方法がある場合 Yes を、ない場合 No を出力せよ。
入力例 1
5 4 2 4 2 1 3 3 5 2 4 1 3 2 4
出力例 1
Yes No
1 番目のクエリで、道 1, 2, 3, 4 の強さをそれぞれ 1, -1, 1, -1 に設定した時を考えます。
このとき、人 1 は体力 0 の状態で町 4 を出発し、体力 1 の状態で町 3 を訪れ、体力 0 の状態で町 2 に到着します。
人 2 は体力 0 の状態で町 1 を出発し、体力 1 の状態で町 2 を訪れ、体力 0 の状態で町 3 に到着します。
人 3 は体力 0 の状態で町 3 を出発し、体力 1 の状態で町 4 を訪れ、体力 0 の状態で町 5 に到着します。
よってこの設定方法は人 1,2,3 の要求をすべて満たすので、 1 行目には Yes を出力します。
2 番目のクエリでは、人 2, 3, 4 の要求をすべて満たすことは不可能なので No を出力します。
入力例 2
7 6 3 1 5 2 4 4 6 7 1 5 3 1 6 1 6 4 4 2 5
出力例 2
No Yes Yes
Score : 900 points
Problem Statement
There are N towns, numbered 1,2,\ldots,N, arranged in a line in this order.
There are N-1 roads connecting adjacent towns: road j\,(1 \leq j \leq N-1) connects towns j and j+1. For each road j, you can set a strength w_j (an integer that may be negative).
When a person travels along a road, their stamina changes. Specifically, if a person with stamina x travels along road j, their stamina becomes x + w_j.
There are M people who will now move between these towns.
Person i\,(1 \le i \le M) starts with stamina 0 at town S_i and travels to town T_i via the shortest path. It is guaranteed that |S_i - T_i| > 1. Also, (S_i, T_i) \neq (S_j, T_j) if i \neq j.
Person i’s requirement is as follows:
When departing Town S_i and when arriving at Town T_i, their stamina should be exactly 0. At every other town, their stamina should always be a positive integer.
Assume that there are no changes to stamina other than those due to traveling along roads as described above.
Process Q queries. For the k-th query (1 \le k \le Q), if it is possible to set the strengths of the roads so that the requirements of all people L_k, L_k + 1, \ldots, R_k are satisfied, print Yes; otherwise, print No.
Constraints
- 3 \le N \le 4 \times 10^5
- 1 \le M \le 2 \times 10^5
- 1 \le Q \le 2 \times 10^5
- 1 \le S_i, T_i \le N
- |S_i - T_i| > 1
- (S_i, T_i) \neq (S_j, T_j)\,(i \neq j)
- 1 \le L_k \le R_k \le M
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M Q S_1 T_1 S_2 T_2 \vdots S_M T_M L_1 R_1 L_2 R_2 \vdots L_Q R_Q
Output
Print Q lines.
The k-th line should contain Yes if there is a way to set the strengths of the roads so that the requirements of all people L_k, L_k + 1, \ldots, R_k are satisfied, and No otherwise.
Sample Input 1
5 4 2 4 2 1 3 3 5 2 4 1 3 2 4
Sample Output 1
Yes No
For the first query, consider setting the strengths of roads 1, 2, 3, 4 to 1, -1, 1, -1, respectively.
- Person 1 starts at town 4 with stamina 0, visits town 3 with stamina 1, and arrives at town 2 with stamina 0.
- Person 2 starts at town 1 with stamina 0, visits town 2 with stamina 1, and arrives at town 3 with stamina 0.
- Person 3 starts at town 3 with stamina 0, visits town 4 with stamina 1, and arrives at town 5 with stamina 0.
Thus, this configuration satisfies the requirements of persons 1,2,3, so print Yes on the first line.
For the second query, it is impossible to satisfy the requirements of persons 2,3,4 simultaneously, so print No.
Sample Input 2
7 6 3 1 5 2 4 4 6 7 1 5 3 1 6 1 6 4 4 2 5
Sample Output 2
No Yes Yes