Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 300 点
問題文
x 軸上に N 個の観光スポットがあり、1, 2, ..., N の番号がついています。 観光スポット i は座標 A_i の点にあります。 また、x 軸上を座標 a の点から座標 b の点まで移動するには |a - b| 円かかります。
あなたは x 軸上を旅行する計画を立てました。 計画では、最初に座標 0 の点を出発し、N 個の観光スポットを番号順に訪れ、最後に座標 0 の点に戻ってくることになっています。
ところが、旅行の直前に急用が入り、N 個すべての観光スポットを訪れる時間的余裕がなくなってしまいました。 そこで、ある i を選び、観光スポット i を訪れるのを取りやめることにしました。 それ以外の観光スポットは予定通り番号順に訪れます。 また、最初に座標 0 の点を出発し、最後に座標 0 の点に戻ってくることについても、予定に変更はありません。
i = 1, 2, ..., N それぞれについて、観光スポット i を訪れるのを取りやめたときの、旅行中の移動にかかる金額の総和を求めてください。
制約
- 2 \leq N \leq 10^5
- -5000 \leq A_i \leq 5000 (1 \leq i \leq N)
- 入力値はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 ... A_N
出力
N 行出力せよ。 このうち i 行目には、観光スポット i を訪れるのを取りやめたときの、旅行中の移動にかかる金額の総和を出力せよ。
入力例 1
3 3 5 -1
出力例 1
12 8 10
観光スポット 1, 2, 3 はそれぞれ座標 3, 5, -1 の点にあります。 各 i について、観光スポット i を訪れるのを取りやめた場合の移動経路および移動にかかる金額は以下のようになります。
- i = 1 のとき、移動経路は 0 \rightarrow 5 \rightarrow -1 \rightarrow 0 となり、移動にかかる金額は 5 + 6 + 1 = 12 円となります。
- i = 2 のとき、移動経路は 0 \rightarrow 3 \rightarrow -1 \rightarrow 0 となり、移動にかかる金額は 3 + 4 + 1 = 8 円となります。
- i = 3 のとき、移動経路は 0 \rightarrow 3 \rightarrow 5 \rightarrow 0 となり、移動にかかる金額は 3 + 2 + 5 = 10 円となります。
入力例 2
5 1 1 1 2 0
出力例 2
4 4 4 2 4
入力例 3
6 -679 -2409 -3258 3095 -3291 -4462
出力例 3
21630 21630 19932 8924 21630 19288
Score : 300 points
Problem Statement
There are N sightseeing spots on the x-axis, numbered 1, 2, ..., N. Spot i is at the point with coordinate A_i. It costs |a - b| yen (the currency of Japan) to travel from a point with coordinate a to another point with coordinate b along the axis.
You planned a trip along the axis. In this plan, you first depart from the point with coordinate 0, then visit the N spots in the order they are numbered, and finally return to the point with coordinate 0.
However, something came up just before the trip, and you no longer have enough time to visit all the N spots, so you decided to choose some i and cancel the visit to Spot i. You will visit the remaining spots as planned in the order they are numbered. You will also depart from and return to the point with coordinate 0 at the beginning and the end, as planned.
For each i = 1, 2, ..., N, find the total cost of travel during the trip when the visit to Spot i is canceled.
Constraints
- 2 \leq N \leq 10^5
- -5000 \leq A_i \leq 5000 (1 \leq i \leq N)
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N A_1 A_2 ... A_N
Output
Print N lines. In the i-th line, print the total cost of travel during the trip when the visit to Spot i is canceled.
Sample Input 1
3 3 5 -1
Sample Output 1
12 8 10
Spot 1, 2 and 3 are at the points with coordinates 3, 5 and -1, respectively. For each i, the course of the trip and the total cost of travel when the visit to Spot i is canceled, are as follows:
- For i = 1, the course of the trip is 0 \rightarrow 5 \rightarrow -1 \rightarrow 0 and the total cost of travel is 5 + 6 + 1 = 12 yen.
- For i = 2, the course of the trip is 0 \rightarrow 3 \rightarrow -1 \rightarrow 0 and the total cost of travel is 3 + 4 + 1 = 8 yen.
- For i = 3, the course of the trip is 0 \rightarrow 3 \rightarrow 5 \rightarrow 0 and the total cost of travel is 3 + 2 + 5 = 10 yen.
Sample Input 2
5 1 1 1 2 0
Sample Output 2
4 4 4 2 4
Sample Input 3
6 -679 -2409 -3258 3095 -3291 -4462
Sample Output 3
21630 21630 19932 8924 21630 19288
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 500 点
問題文
2 つの整数 A, B が与えられます。
各マスが白または黒に塗られたグリッドであって以下の条件を満たすものを、出力の項で指定されたフォーマットに従って一つ出力してください。
- グリッドの大きさを縦 h 行横 w 列としたとき、h および w はともに 100 以下である。
- 白く塗られたマスの集合はちょうど A 個の連結成分に分かれている (連結成分という単語の定義については後の注釈を参照)。
- 黒く塗られたマスの集合はちょうど B 個の連結成分に分かれている。
制約の項で指定される条件のもとで解は必ず一つ以上存在することが証明できます。 解が複数ある場合、どれを出力しても構いません。
注釈
2 つの白く塗られたマス c_1, c_2が連結であるとは、マス c_1 からマス c_2 へ、上下左右に隣り合うマスへの移動を繰り返して、 白く塗られたマスだけを通って移動できることを意味します。
白く塗られたマスの集合 S が連結成分であるとは、S が以下の条件を満たすことを意味します。
- S のどの 2 つのマスも連結である。
- S に含まれないどの白く塗られたマスと、S に含まれるどのマスも連結ではない。
黒く塗られたマスについても連結成分を同様に定義します。
制約
- 1 \leq A \leq 500
- 1 \leq B \leq 500
入力
入力は以下の形式で標準入力から与えられる。
A B
出力
以下の形式で出力せよ。
- 1 行目には構成したグリッドの大きさを表す整数 h, w を空白を区切りとして出力せよ。
- 続いて h 行出力せよ。このうちの i 行目 (1 \leq i \leq h) には以下のような長さ w の文字列 s_i を出力せよ。
- 構成したグリッドの i 行 j (1 \leq j \leq w) 列のマスが白く塗られているならば、s_i の j 文字目は
.である。 - 構成したグリッドの i 行 j (1 \leq j \leq w) 列のマスが黒く塗られているならば、s_i の j 文字目は
#である。
- 構成したグリッドの i 行 j (1 \leq j \leq w) 列のマスが白く塗られているならば、s_i の j 文字目は
入力例 1
2 3
出力例 1
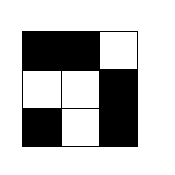
3 3 ##. ..# #.#
この出力は以下のグリッドに対応します。
入力例 2
7 8
出力例 2
3 5 #.#.# .#.#. #.#.#
入力例 3
1 1
出力例 3
4 2 .. #. ## ##
入力例 4
3 14
出力例 4
8 18 .................. .................. ....##.......####. ....#.#.....#..... ...#...#....#..... ..#.###.#...#..... .#.......#..#..... #.........#..####.
Score : 500 points
Problem Statement
You are given two integers A and B.
Print a grid where each square is painted white or black that satisfies the following conditions, in the format specified in Output section:
- Let the size of the grid be h \times w (h vertical, w horizontal). Both h and w are at most 100.
- The set of the squares painted white is divided into exactly A connected components.
- The set of the squares painted black is divided into exactly B connected components.
It can be proved that there always exist one or more solutions under the conditions specified in Constraints section. If there are multiple solutions, any of them may be printed.
Notes
Two squares painted white, c_1 and c_2, are called connected when the square c_2 can be reached from the square c_1 passing only white squares by repeatedly moving up, down, left or right to an adjacent square.
A set of squares painted white, S, forms a connected component when the following conditions are met:
- Any two squares in S are connected.
- No pair of a square painted white that is not included in S and a square included in S is connected.
A connected component of squares painted black is defined similarly.
Constraints
- 1 \leq A \leq 500
- 1 \leq B \leq 500
Input
Input is given from Standard Input in the following format:
A B
Output
Output should be in the following format:
- In the first line, print integers h and w representing the size of the grid you constructed, with a space in between.
- Then, print h more lines. The i-th (1 \leq i \leq h) of these lines should contain a string s_i as follows:
- If the square at the i-th row and j-th column (1 \leq j \leq w) in the grid is painted white, the j-th character in s_i should be
.. - If the square at the i-th row and j-th column (1 \leq j \leq w) in the grid is painted black, the j-th character in s_i should be
#.
- If the square at the i-th row and j-th column (1 \leq j \leq w) in the grid is painted white, the j-th character in s_i should be
Sample Input 1
2 3
Sample Output 1
3 3 ##. ..# #.#
This output corresponds to the grid below:

Sample Input 2
7 8
Sample Output 2
3 5 #.#.# .#.#. #.#.#
Sample Input 3
1 1
Sample Output 3
4 2 .. #. ## ##
Sample Input 4
3 14
Sample Output 4
8 18 .................. .................. ....##.......####. ....#.#.....#..... ...#...#....#..... ..#.###.#...#..... .#.......#..#..... #.........#..####.
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 900 点
問題文
N 頂点 M 辺からなる重み付き無向グラフがあります。 グラフの i 番目の辺は頂点 U_i と頂点 V_i を結んでおり、重みは W_i です。 さらに、整数 X が与えられます。
このグラフの各辺を白または黒に塗る方法であって、以下の条件を満たすものの個数を 10^9 + 7 で割ったあまりを求めてください。
- 白く塗られた辺と黒く塗られた辺をともに含む全域木が存在する。さらに、そのような全域木のうち最も重みが小さいものの重みは X である。
ただし、全域木の重みとは、その全域木に含まれる辺の重みの和を表します。
制約
- 1 \leq N \leq 1,000
- 1 \leq M \leq 2,000
- 1 \leq U_i, V_i \leq N (1 \leq i \leq M)
- 1 \leq W_i \leq 10^9 (1 \leq i \leq M)
- i \neq j のとき、(U_i, V_i) \neq (U_j, V_j) かつ (U_i, V_i) \neq (V_j, U_j)
- U_i \neq V_i (1 \leq i \leq M)
- 与えられるグラフは連結である。
- 1 \leq X \leq 10^{12}
- 入力値はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
N M X U_1 V_1 W_1 U_2 V_2 W_2 : U_M V_M W_M
出力
答えを出力せよ。
入力例 1
3 3 2 1 2 1 2 3 1 3 1 1
出力例 1
6
入力例 2
3 3 3 1 2 1 2 3 1 3 1 2
出力例 2
2
入力例 3
5 4 1 1 2 3 1 3 3 2 4 6 2 5 8
出力例 3
0
入力例 4
8 10 49 4 6 10 8 4 11 5 8 9 1 8 10 3 8 128773450 7 8 10 4 2 4 3 4 1 3 1 13 5 2 2
出力例 4
4
Score : 900 points
Problem Statement
We have an undirected weighted graph with N vertices and M edges. The i-th edge in the graph connects Vertex U_i and Vertex V_i, and has a weight of W_i. Additionally, you are given an integer X.
Find the number of ways to paint each edge in this graph either white or black such that the following condition is met, modulo 10^9 + 7:
- The graph has a spanning tree that contains both an edge painted white and an edge painted black. Furthermore, among such spanning trees, the one with the smallest weight has a weight of X.
Here, the weight of a spanning tree is the sum of the weights of the edges contained in the spanning tree.
Constraints
- 1 \leq N \leq 1 000
- 1 \leq M \leq 2 000
- 1 \leq U_i, V_i \leq N (1 \leq i \leq M)
- 1 \leq W_i \leq 10^9 (1 \leq i \leq M)
- If i \neq j, then (U_i, V_i) \neq (U_j, V_j) and (U_i, V_i) \neq (V_j, U_j).
- U_i \neq V_i (1 \leq i \leq M)
- The given graph is connected.
- 1 \leq X \leq 10^{12}
- All input values are integers.
Input
Input is given from Standard Input in the following format:
N M X U_1 V_1 W_1 U_2 V_2 W_2 : U_M V_M W_M
Output
Print the answer.
Sample Input 1
3 3 2 1 2 1 2 3 1 3 1 1
Sample Output 1
6
Sample Input 2
3 3 3 1 2 1 2 3 1 3 1 2
Sample Output 2
2
Sample Input 3
5 4 1 1 2 3 1 3 3 2 4 6 2 5 8
Sample Output 3
0
Sample Input 4
8 10 49 4 6 10 8 4 11 5 8 9 1 8 10 3 8 128773450 7 8 10 4 2 4 3 4 1 3 1 13 5 2 2
Sample Output 4
4
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1100 点
問題文
2^N 人の選手がおり、それぞれ 1, 2, ..., 2^N の番号がついています。 これらの選手でトーナメントを行うことにしました。
トーナメントは以下のようにして行われます。
- 1, 2, ..., 2^N の置換 p_1, p_2, ..., p_{2^N} を選ぶ。
- 選手たちが選手 p_1, 選手 p_2, ..., 選手 p_{2^N} の順に一列に並ぶ。
- 列に残っている選手が 1 人だけになるまで、以下を繰り返す。
- 列の前から 1 番目と 2 番目、3 番目と 4 番目、... の選手が対戦を行う。 負けた選手は列から離れる。勝った選手たちは相対順序を保ったまま改めて一列に並ぶ。
- 最後まで残った選手が優勝である。
2 人の選手が対戦したときの結果は、入力として与えられる M 個の 整数 A_1, A_2, ..., A_M を用いて以下のように書けることが分かっています。
- ある i について y = A_i のとき、選手 1 と選手 y (2 \leq y \leq 2^N) が対戦すると選手 y が勝つ。
- どの i についても y \neq A_i のとき、選手 1 と選手 y (2 \leq y \leq 2^N) が対戦すると選手 1 が勝つ。
- 2 \leq x < y \leq 2^N のとき、選手 x と選手 y が対戦すると選手 x が勝つ。
このトーナメントの優勝者は、最初に選ぶ置換 p_1, p_2, ..., p_{2^N} だけに依存します。 トーナメントを行う際に最初に選ぶ置換 p_1, p_2, ..., p_{2^N} であって、 トーナメントの結果選手 1 が優勝するようなものの個数を 10^9 + 7 で割ったあまりを求めてください。
制約
- 1 \leq N \leq 16
- 0 \leq M \leq 16
- 2 \leq A_i \leq 2^N (1 \leq i \leq M)
- A_i < A_{i + 1} (1 \leq i < M)
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 ... A_M
出力
答えを出力せよ。
入力例 1
2 1 3
出力例 1
8
条件を満たす p としては [1, 4, 2, 3] や [3, 2, 1, 4] などが、条件を満たさない p としては [1, 2, 3, 4] や [1, 3, 2, 4] などがあります。
入力例 2
4 3 2 4 6
出力例 2
0
入力例 3
3 0
出力例 3
40320
入力例 4
3 3 3 4 7
出力例 4
2688
入力例 5
16 16 5489 5490 5491 5492 5493 5494 5495 5497 18993 18995 18997 18999 19000 19001 19002 19003
出力例 5
816646464
Score : 1100 points
Problem Statement
There are 2^N players, numbered 1, 2, ..., 2^N. They decided to hold a tournament.
The tournament proceeds as follows:
- Choose a permutation of 1, 2, ..., 2^N: p_1, p_2, ..., p_{2^N}.
- The players stand in a row in the order of Player p_1, Player p_2, ..., Player p_{2^N}.
- Repeat the following until there is only one player remaining in the row:
- Play the following matches: the first player in the row versus the second player in the row, the third player versus the fourth player, and so on. The players who lose leave the row. The players who win stand in a row again, preserving the relative order of the players.
- The last player who remains in the row is the champion.
It is known that, the result of the match between two players can be written as follows, using M integers A_1, A_2, ..., A_M given as input:
- When y = A_i for some i, the winner of the match between Player 1 and Player y (2 \leq y \leq 2^N) will be Player y.
- When y \neq A_i for every i, the winner of the match between Player 1 and Player y (2 \leq y \leq 2^N) will be Player 1.
- When 2 \leq x < y \leq 2^N, the winner of the match between Player x and Player y will be Player x.
The champion of this tournament depends only on the permutation p_1, p_2, ..., p_{2^N} chosen at the beginning. Find the number of permutation p_1, p_2, ..., p_{2^N} chosen at the beginning of the tournament that would result in Player 1 becoming the champion, modulo 10^9 + 7.
Constraints
- 1 \leq N \leq 16
- 0 \leq M \leq 16
- 2 \leq A_i \leq 2^N (1 \leq i \leq M)
- A_i < A_{i + 1} (1 \leq i < M)
Input
Input is given from Standard Input in the following format:
N M A_1 A_2 ... A_M
Output
Print the answer.
Sample Input 1
2 1 3
Sample Output 1
8
Examples of p that satisfy the condition are: [1, 4, 2, 3] and [3, 2, 1, 4]. Examples of p that do not satisfy the condition are: [1, 2, 3, 4] and [1, 3, 2, 4].
Sample Input 2
4 3 2 4 6
Sample Output 2
0
Sample Input 3
3 0
Sample Output 3
40320
Sample Input 4
3 3 3 4 7
Sample Output 4
2688
Sample Input 5
16 16 5489 5490 5491 5492 5493 5494 5495 5497 18993 18995 18997 18999 19000 19001 19002 19003
Sample Output 5
816646464