実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 900 点
問題文
音楽に合わせて数直線上を走り回る、次のようなゲームを考えます。
数直線上に N 個のボタンがあります。i 番目 (1 \leq i \leq N) のボタンは、ゲーム開始 T_i 秒後に座標 X_i に出現します。 また、どのボタンについても出現から D+0.5 秒後に消えます。
プレイヤーは、ゲーム開始時に座標 0 を出発し、N 個すべてのボタンを押すことができればゲームクリアとなります。ボタンは好きな順番で押して構いません。 しかし、本ゲームには特殊ルールがあり、ボタンを押してから次にボタンを押すまでの間に、毎回一度以上座標 0 に移動する必要があります。 それが守られない場合は失格となります。
AtCoder さんは、数直線上を秒速 1 で移動することができます。彼女がゲームクリアする方法は存在しますか。 ただし、ボタンを押すのにかかる時間は無視できるものとします。
\mathrm{TESTCASES} 個のテストケースについて解いてください。
制約
- 1 \leq \mathrm{TESTCASES} \leq 100\,000
- 1 \leq N \leq 5\,000
- 0 \leq D \leq 10^{12}
- 0 \leq T_1 \leq T_2 \leq \dots \leq T_N \leq 10^{12}
- 1 \leq X_i \leq 10^{12}
- すべてのテストケースに対する N の総和は 100\,000 以下である
- すべてのテストケースに対する N^2 の総和は 2.5 \times 10^7 以下である
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられます。ここで、\mathrm{case}_k は k 番目のテストケースを意味します。
\mathrm{TESTCASES}
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_{\mathrm{TESTCASES}}
各テストケースは、以下の形式で与えられます。
N D T_1 X_1 T_2 X_2 \vdots T_N X_N
出力
\mathrm{TESTCASES} 行出力してください。k 行目には、k 番目のテストケースについて、ゲームクリアする方法が存在するならば Yes、存在しないならば No と出力してください。
入力例 1
4 2 10 30 20 50 10 2 9 30 20 50 10 4 185 0 40 0 30 0 20 0 10 5 1312372641 141421356 314159265 237309504 358979323 880168872 846264338 4209698078 327950288 5696718753 419716939
出力例 1
Yes No Yes No
1 番目のテストケースでは、以下のように動くとゲームクリアとなります。そのため、1 行目に Yes と出力します。
| 開始からの時間 | 動作・出来事の説明 |
|---|---|
| 0 秒 | ゲームが開始する。 |
| 5 秒 | 座標 0 から右方向に移動を開始する。 |
| 25 秒 | 座標 20 に到着し、停止する。 |
| 30 秒 | 1 番目のボタンが座標 20 に出現する。ただちにこのボタンを押し、左方向に移動を開始する。 |
| 50 秒 | 座標 0 に到着する。移動方向を右方向に変える。ちょうどそのタイミングで、2 番目のボタンが座標 10 に出現する。 |
| 60 秒 | 座標 10 に到着し、2 番目のボタンを押す。このボタンは開始 60.5 秒後に消えるので、間に合っている。 |
2 番目のテストケースについては、ゲームクリアする方法が存在しないので、2 行目に No と出力します。
3 番目のテストケースについては、ゲームクリアする方法が存在するので、3 行目に Yes と出力します。
4 番目のテストケースについては、ゲームクリアする方法が存在しないので、4 行目に No と出力します。
Score : 900 points
Problem Statement
Consider the following rhythm‑action game on the real line.
There are N buttons. The i‑th button (1 \le i \le N) appears at coordinate X_i exactly T_i seconds after the game starts. Each button disappears D + 0.5 seconds after it appears.
The player starts at coordinate 0 at time 0, and must press all N buttons to win the game. The buttons may be pressed in any order. However, after pressing a button and before pressing another, the player must visit coordinate 0 at least once. Violating this rule results in disqualification.
Ms. AtCoder can move at speed 1 on the line. Can she win the game? Pressing a button takes negligible time.
Solve \mathrm{TESTCASES} test cases.
Constraints
- 1 \le \mathrm{TESTCASES} \le 100\,000
- 1 \le N \le 5\,000
- 0 \le D \le 10^{12}
- 0 \le T_1 \le T_2 \le \dots \le T_N \le 10^{12}
- 1 \le X_i \le 10^{12}
- The sum of N over all test cases is at most 100\,000.
- The sum of N^2 over all test cases is at most 2.5 \times 10^7.
- All input values are integers.
Input
The input is given from Standard Input in the following format, where \mathrm{case}_k represents the k-th test case:
\mathrm{TESTCASES}
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_{\mathrm{TESTCASES}}
Each test case is given in the following format:
N D T_1 X_1 T_2 X_2 \vdots T_N X_N
Output
Print \mathrm{TESTCASES} lines. The k-th line should contain Yes if the game is winnable for the k-th test case, and No otherwise.
Sample Input 1
4 2 10 30 20 50 10 2 9 30 20 50 10 4 185 0 40 0 30 0 20 0 10 5 1312372641 141421356 314159265 237309504 358979323 880168872 846264338 4209698078 327950288 5696718753 419716939
Sample Output 1
Yes No Yes No
For the first test case, the game can be won as follows, so the first line contains Yes.
| Elapsed time | Action / Event |
|---|---|
| 0 seconds | Game starts. |
| 5 seconds | Start moving right from coordinate 0. |
| 25 seconds | Arrive at coordinate 20 and stop. |
| 30 seconds | Button 1 appears at coordinate 20. Press it immediately and head left. |
| 50 seconds | Arrive at coordinate 0. Head right. Button 2 appears at coodinate 10. |
| 60 seconds | Arrive at coordinate 10 and press button 2 (before it disappears at 60.5 seconds). |
For the second test case, the game is unwinnable, so the second line contains No.
For the third test case, the game is winnable, so the third line contains Yes.
For the fourth test case, the game is unwinnable, so the fourth line contains No.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1100 点
問題文
AGC 語とは、同じ数の A と C のみからなり、どの接頭辞についても A が半数以上を占める 2 文字以上の文字列を指します。
N 個の A と N 個の C からなる 2N 文字の文字列 S が与えられるので、k = 1, 2, \dots, K について次の問いに答えてください。
黒板に S を k 回繰り返した文字列が書かれている。 以下の操作をその順に行うことで、黒板の文字列を AGC 語にしたい。
- 次の操作を 1 回だけ行う。
- 整数 (l, r) (1 \leq l \leq r \leq 2kN) を選択し、文字列の l から r 文字目までの部分を reverse する。
- 次の操作を 0 回以上行う。
- 文字列の隣接する 2 文字を swap する。
最小何回の swap 操作が必要であるか、計算せよ。
接頭辞とは
文字列 Y が文字列 X の接頭辞であるとは、1 \leq |Y| \leq |X| であり、かつ X の最初の |Y| 文字が Y であることを指します。たとえばATC は ATCODER の接頭辞ですが、AGC や ATCODERGRANDCONTEST は ATCODER の接頭辞ではありません。制約
- 1 \leq N \leq 1\,000\,000
- 1 \leq K \leq 300\,000
- 文字列 S は N 個の
Aと N 個のCからなる 2N 文字の文字列である - N と K は整数
入力
入力は以下の形式で標準入力から与えられます。
N K S
出力
答えを K 行に出力してください。i 行目 (1 \leq i \leq K) には k = i のときの答えを出力してください。
入力例 1
1 2 AC
出力例 1
0 0
k = 1 のとき、最初黒板に書かれた文字列は AC となります。
k = 2 のとき、最初黒板に書かれた文字列は ACAC となります。
両方とも最初から AGC 語であるため、たとえば (l, r) = (1, 1) とすると、0 回の swap 操作を達成することができます。
入力例 2
5 1 CACAAACCCA
出力例 2
1
k = 1 のとき、黒板に書かれる文字列は CACAAACCCA となります。以下の手順で操作を行うと、swap 操作を 1 回しか行う必要がありません。
- (l, r) = (1, 4) を選択し、文字列の 1 から 4 文字目を reverse する。文字列は
ACACAACCCAとなる。 - 文字列の 9 文字目と 10 文字目を swap する。文字列は
ACACAACCACとなり、これは AGC 語である。
入力例 3
10 10 ACCCAAAACCCACCACAACA
出力例 3
1 2 3 3 3 3 3 3 3 3
入力例 4
50 10 ACCCCACAACAAAACCAACCCCACCAACACCAAAACACACAAAACCCCCACCAACACAACAACCCCAACAAACCCAACACACCCACACCAAACCCAAACA
出力例 4
10 17 20 22 23 24 25 26 26 26
入力例 5
72 10 CCCCACAAAAACCCACACCAAACCACCCCCAAAAACACCACCCCCAAAAAAACAAAAAACCCCCCACCCAAACAACACCACCACAAACCCAACCAACAACCCAAAACAACCCCACCACACACCACACCCACAAACACAACAACA
出力例 5
28 42 51 54 57 60 63 64 65 66
Score : 1100 points
Problem Statement
An AGC word is a string of length at least 2 that contains the same number of A’s and C’s, and in every prefix, A’s make up at least half of the characters.
You are given a string S of length 2N consisting of N A’s and N C’s. For each k = 1, 2, \dots, K, answer the following question.
A blackboard shows a string that is a concatenation of k copies of S. To turn it into an AGC word, perform the operations below in the order written:
- Perform exactly once:
- Choose integers (l, r) (1 \le l \le r \le 2kN) and reverse the l-th through r-th characters of the string.
- Perform zero or more times:
- Swap two adjacent characters of the string.
What is the minimum number of swaps required?
Notes on prefix
A string Y is a prefix of X if and only if 1 \le |Y| \le |X| and the first |Y| characters of X equal Y. For example,ATC is a prefix of ATCODER, but AGC and ATCODERGRANDCONTEST are not.
Constraints
- 1 \le N \le 1\,000\,000
- 1 \le K \le 300\,000
- S is a length‑2N string consisting of N
A’s and NC’s. - N and K are integers.
Input
The input is given from Standard Input in the following format:
N K S
Output
Print K lines. The i‑th line (1 \le i \le K) should contain the answer for k = i.
Sample Input 1
1 2 AC
Sample Output 1
0 0
For k = 1, the initial string is AC;
For k = 2, it is ACAC.
Both are already AGC words, so choosing, say, (l, r) = (1, 1) yields 0 swaps.
Sample Input 2
5 1 CACAAACCCA
Sample Output 2
1
For k = 1, the string is CACAAACCCA. By following the steps below, the sequence needs only one swap:
- Choose (l, r) = (1, 4) and reverse the 1-st through 4-th characters. The string is now
ACACAACCCA. - Swap the 9-th and 10-th characters. The string is now
ACACAACCAC, which is an AGC word.
Sample Input 3
10 10 ACCCAAAACCCACCACAACA
Sample Output 3
1 2 3 3 3 3 3 3 3 3
Sample Input 4
50 10 ACCCCACAACAAAACCAACCCCACCAACACCAAAACACACAAAACCCCCACCAACACAACAACCCCAACAAACCCAACACACCCACACCAAACCCAAACA
Sample Output 4
10 17 20 22 23 24 25 26 26 26
Sample Input 5
72 10 CCCCACAAAAACCCACACCAAACCACCCCCAAAAACACCACCCCCAAAAAAACAAAAAACCCCCCACCCAAACAACACCACCACAAACCCAACCAACAACCCAAAACAACCCCACCACACACCACACCCACAAACACAACAACA
Sample Output 5
28 42 51 54 57 60 63 64 65 66
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1100 点
問題文
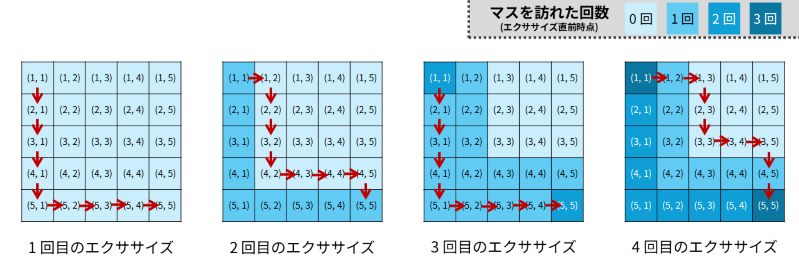
AtCoder 市は N \times N のマス目で表されます。上から i 番目 (1 \leq i \leq N)、左から j 番目 (1 \leq j \leq N) のマスは、(i, j) と表されます。
青木君は、近日行われるマラソン大会に向けて、以下の手順からなる エクササイズ を K 回行いました。
- マス (1, 1) を出発する。
- 以下を 2N-2 回繰り返して、マス (N, N) に到着する。
- 下方向または右方向に 1 マス進む。ただし、下方向のマスと右方向のマスの両方に移動できる場合、今までのエクササイズで「そのマスを訪れた回数」が少ない方を選ぶ。同数の場合は下方向を選ぶ。
それでは、K 回目のエクササイズで通る経路を求めてください。
制約
- 2 \leq N \leq 100
- 1 \leq K \leq 10^{18}
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられます。
N K
出力
長さ 2N-2 の文字列を出力してください。この i 文字目は、K 回目のエクササイズにおける i 回目の移動で下方向に動いた場合は D、右方向に動いた場合は R としてください。
入力例 1
5 4
出力例 1
RRDDRRDD
1, 2, 3, 4 回目のエクササイズでは以下の図のように動くことになります。よって、答えは RRDDRRDD です。
入力例 2
10 869120
出力例 2
RDRRRDRDRDRDRDDDRD
Score : 1100 points
Problem Statement
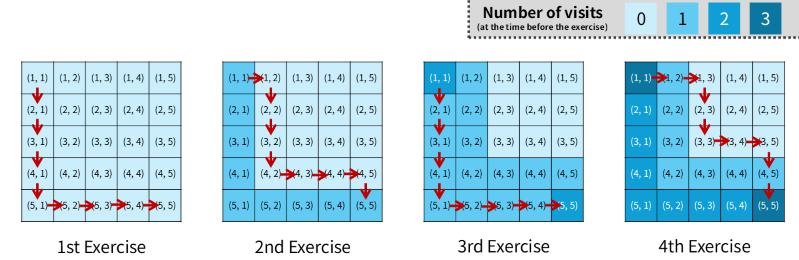
AtCoder City is represented by an N \times N grid. Let (i, j) denote the cell at the i‑th row from the top (1 \le i \le N) and the j‑th column from the left (1 \le j \le N).
Aoki performed the following exercise K times for marathon training.
- Start from cell (1, 1).
- Repeat the following action 2N-2 times to reach cell (N, N):
- Move one cell down or right. If both moves are possible, choose the one whose destination cell has been visited fewer times in the previous exercises. If the counts are equal, choose the downward move.
Print the path taken in the K‑th exercise.
Constraints
- 2 \le N \le 100
- 1 \le K \le 10^{18}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N K
Output
Print a string of length 2N-2. The i‑th character should be D if the i‑th move in the K‑th exercise goes downward, and R if it goes rightward.
Sample Input 1
5 4
Sample Output 1
RRDDRRDD
The 1st, 2nd, 3rd, and 4th exercises go as follows, so the answer is RRDDRRDD.
Sample Input 2
10 869120
Sample Output 2
RDRRRDRDRDRDRDDDRD
実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 1400 点
問題文
これはインタラクティブな問題です。
机の上に {}_{2N}\mathrm{C}_N 枚のカードがあり、1 から {}_{2N}\mathrm{C}_N までの番号が付けられています。カード i (1 \leq i \leq {}_{2N}\mathrm{C}_N) のオモテ面には、N 個の 0 と N 個の 1 からなる {}_{2N}\mathrm{C}_N 種類の文字列のうち、辞書順で i 番目に小さいものが印刷されています。
具体例
たとえば N=2 の場合、カード 1, 2, 3, 4, 5, 6 のオモテ面にはそれぞれ0011、0101、0110、1001、1010、1100 が印刷されます。魔女の Alice は、各カードのウラ面に最初の N 個の英大文字(たとえば N=2 の時 A, B)のいずれかを書き、その後以下のマジックを T 回行います。
一回のマジックの流れ
- 司会者が、最初の N 個の英大文字のいずれか s を宣言する。
- 司会者が、黒板に
0のみからなる長さ 2N の文字列を書く。- i = 1, 2, \dots, N の順に以下の行動を行う。ただし a_1, b_1, \dots, a_N, b_N は 1 以上 2N 以下の相異なる整数である。
- まず、司会者が Alice に整数 a_i と b_i を伝える。
- 次に、Alice が黒板の文字列の a_i 文字目と b_i 文字目のうち片方だけを
1に変える。- 黒板の文字列を x とする。x がオモテ面に書き込まれたカードがちょうど一枚あるので、そのウラ面を見る。ウラ面に書かれた文字が s であれば、マジックは成功、そうでなければマジックは失敗である。
ここで、Alice は a_i 文字目と b_i 文字目のうち片方を 1 に変えるまで、a_{i+1}, b_{i+1} の情報を知ることができないことに注意する必要があります。
T 回すべてのマジックで成功する戦略を実装してください。では、始めましょう。
制約
- 2 \leq N \leq 10
- 1 \leq T \leq 5\,000
- s は最初の N 個の英大文字のいずれかである
- 1 \leq a_i < b_i \leq 2N
- a_1, b_1, a_2, b_2, \dots, a_N, b_N は相異なる
- a_1, b_1, a_2, b_2, \dots, a_N, b_N, s はジャッジとの対話前に決定される
- N, T, a_i, b_i は整数
入出力
最初に、整数 N, T を標準入力から以下の形式で受け取ってください。
N T
次に、カード i のウラ面に書き込む文字を c_i とするとき、以下の形式で出力してください。末尾に改行を入れてください。ここで、c_i は最初の N 個の英大文字のいずれかである必要があります。
c_1 c_2 \cdots c_{{}_{2N}\mathrm{C}_N}
次に、以下の処理を T 回繰り返してください。t 回目 (1 \leq t \leq T) の処理は t 回目のマジックに対応します。
まず、司会者が宣言した文字 s を以下の形式で標準入力から受け取る。
s続いて、i = 1, 2, \dots, N の順に以下の処理を行う。
- まず、整数 a_i, b_i を以下の形式で入力する。
a_i b_i
- 次に、
1に変える文字の位置 d を、以下の形式で出力する。d は a_i, b_i のいずれかでなければならない。末尾に改行を入れること。dここで、出力形式にミスがあった場合や、前回のマジックに失敗した場合、それ以降 s や (a_i, b_i) などの入力は与えられず、
-1が標準入力から与えられる。この場合はただちにプログラムを終了すること。(ただし、T 回目のマジックで初めて失敗した場合や、T 回目のマジックの i = N のときに初めて出力形式にミスがあった場合は、その後の入力は何も与えられない)
注意点
出力を行うたびに、ジャッジ結果を flush してください。そうしなかった場合、ジャッジ結果が TLE となることがあります。
また、ジャッジから -1 という入力を受け取った場合はただちにプログラムを終了してください。終了した場合のジャッジ結果は WA となりますが、終了しなかった場合のジャッジ結果は不定です。さらに、余計な改行は不正な形式の出力とみなされることがあるので注意してください。
この問題のジャッジシステムは適応的 (adaptive) ではありません。すなわち、a_1, b_1, a_2, b_2, \dots, a_N, b_N, s の値はジャッジとの対話前に決定され、プログラムの出力によって変更されることはありません。
入出力例
以下に示す例は、対話の一例であることに注意してください。
| 入力 | 出力 | 説明 |
|---|---|---|
2 2 |
まず整数 N と T が標準入力から与えられます。 | |
ABABAB |
6 枚のカードに書き込む文字を出力します。 | |
A |
1 回目のマジックが始まります。 司会者は文字 A を宣言します。 |
|
1 2 |
(a_1, b_1) = (1, 2) であることが司会者から知らされます。 | |
2 |
黒板の 2 文字目を 1 にします。 |
|
3 4 |
(a_2, b_2) = (3, 4) であることが司会者から知らされます。 | |
3 |
黒板の 3 文字目を 1 にします。最終的な黒板の文字列は 0110 となり、オモテ面に 0110 と書かれたカードのウラ面は A なのでマジック成功です。 |
|
B |
2 回目のマジックが始まります。 司会者は文字 B を宣言します。 |
|
1 3 |
(a_1, b_1) = (1, 3) であることが司会者から知らされます。 | |
1 |
黒板の 1 文字目を 1 にします。 |
|
2 4 |
(a_2, b_2) = (2, 4) であることが司会者から知らされます。 | |
2 |
黒板の 2 文字目を 1 にします。最終的な黒板の文字列は 1100 となり、オモテ面に 1100 と書かれたカードのウラ面は B なのでマジック成功です。 |
Score : 1400 points
Problem Statement
This is an interactive problem.
There are \tbinom{2N}{N} cards numbered 1 to \tbinom{2N}{N} on a desk. Card i (1 \le i \le \tbinom{2N}{N}) shows on its front the i‑th string in lexicographic order among the strings consisting of N zeros and N ones.
Example
For N = 2, the fronts of cards 1, 2, 3, 4, 5, 6 are0011, 0101, 0110, 1001, 1010, 1100, respectively.
Witch Alice writes one of the first N uppercase letters (for example, A or B if N = 2) on the back of each card, then performs the following magic T times.
A single magic
- The host announces a letter s among the first N uppercase letters.
- The host writes a length-2N string of all
0on the blackboard.- For i = 1, 2, \dots, N in this order, do the following. Here, a_1, b_1, \dots, a_N, b_N are distinct integers from 1 to 2N.
- First, the host tells Alice integers a_i and b_i.
- Then, Alice chooses exactly one of the a_i-th and b_i-th characters of the string on the blackboard, and sets it to
1.- Let x be the final string on the blackboard. Exactly one card shows x on its front; look at its back. The magic succeeds if and only if the letter on its back equals s.
Note that Alice learns a_{i+1} and b_{i+1} only after choosing which of the a_i-th and b_i-th characters to set to 1.
Implement a strategy that makes all T magics succeed. Now, let us begin.
Constraints
- 2 \le N \le 10
- 1 \le T \le 5\,000
- The letter s is among the first N uppercase letters.
- 1 \le a_i < b_i \le 2N
- a_1, b_1, a_2, b_2, \dots, a_N, b_N are distinct.
- a_1, b_1, a_2, b_2, \dots, a_N, b_N, s are fixed before the interaction starts.
- N, T, a_i, b_i are integers.
Input and Output
First, read the integers N and T given from Standard Input in the following format:
N T
Next, let c_i be the letter written on the back of card i, and print those letters in the following format, followed by a newline. Here, c_i must be among the first N uppercase letters.
c_1 c_2 \cdots c_{\tbinom{2N}{N}}
Next, repeat the following process T times. The t-th iteration (1 \leq t \leq T) corresponds to the t-th magic.
Read the announced letter s given in the following format:
sThen, for i = 1, 2, \dots, N in this order, do the following.
- Read integers a_i and b_i given in the following format:
a_i b_i
- Print the chosen position d in the following format, followed by a newline. Here, d must be a_i or b_i.
dIf your output was malformed or the previous magic failed, no more input such as s or (a_i, b_i) is given, but
-1is given from Standard Input. In this case, exit immediately. (If you fail for the first time in the T-th magic, or your output was malformed for the first time at i = N in the T-th magic, no more input follows.)
Notes
Flush after every output. Otherwise, you may receive a TLE verdict.
If you read -1, exit immediately. If you do so, you will receive a WA verdict, but continuing leads to an indeterminate verdict. Unnecessary newlines may be seen as malformed.
The judge is non‑adaptive; the values a_1, b_1, a_2, b_2, \dots, a_N, b_N, s are fixed before the interaction starts, and will not be affected by your output.
Sample Interaction
Note that this is just an example of interaction.
| Input | Output | Comment |
|---|---|---|
2 2 | The integers N and T are given from Standard Input. | |
ABABAB | Print letters for the backs of the six cards. | |
A | The first magic begins. The host declares A. | |
1 2 | The host tells you (a_1, b_1) = (1, 2). | |
2 | Set the second character to 1. | |
3 4 | The host tells you (a_2, b_2) = (3, 4). | |
3 | Set the third character to 1.The final string is 0110, and the card with 0110 on its front has A on the back, so the magic succeeds. | |
B | The second magic begins. The host declars B. | |
1 3 | The host tells you (a_1, b_1) = (1, 3). | |
1 | Set the first character to 1. | |
2 4 | The host tells you (a_2, b_2) = (2, 4). | |
2 | Set the second character to 1.The final string is 1100, and the card with 1100 on its front has B on the back, so the magic succeeds. |
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 1400 点
問題文
日本には N 個の空港があり、それぞれに 1, 2, \dots, N と番号が付けられています。AtCoder 航空は、日本で M 本の航空路線を運航しており、それぞれに 1, 2, \dots, M と番号が付けられています。航空路線 j は空港 A_j を出発し空港 B_j に到着するものであり、価格は C_j \times F 円です。
AtCoder 航空で飛行機に乗ると「マイル」という通貨を得ることができます。最初の時点では 0 マイル持っています。航空路線 j に一回乗ると C_j マイルを得ます。また、空港 i では 1 マイル当たり R_i 円に換金することができます。なお、制約 0 \leq R_i \leq F-1 より、飛行機を乗り継いで無制限にお金を得ることはできません。
ここで、換金するマイルや所持金は整数にならなくてもかまいませんが、マイルや所持金が負の数になってはいけません。
さて、空港 1 から空港 N に飛行機で行くために、最初に何円以上持っている必要があるでしょうか?
\mathrm{TESTCASES} 個のテストケースについて解いてください。
制約
- 1 \leq \mathrm{TESTCASES} \leq 40\,000
- 2 \leq N \leq 400
- 1 \leq M \leq N \times (N-1)
- 1 \leq F \leq 100
- 1 \leq A_j \leq N
- 1 \leq B_j \leq N
- A_j \neq B_j
- (A_1, B_1), (A_2, B_2), \dots, (A_M, B_M) はすべて異なる
- 1 \leq C_j \leq 100
- 0 \leq R_i \leq F-1
- 空港 1 から空港 N に行く方法が存在する
- すべてのテストケースに対する N^2 の総和は 160\,000 以下である
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられます。ここで、\mathrm{case}_k は k 番目のテストケースを意味します。
\mathrm{TESTCASES}
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_{\mathrm{TESTCASES}}
各テストケースは、以下の形式で与えられます。
N M F A_1 B_1 C_1 A_2 B_2 C_2 \vdots A_M B_M C_M R_1 R_2 \cdots R_N
出力
\mathrm{TESTCASES} 行出力してください。k 行目には、k 番目のテストケースについて、空港 1 から空港 N に飛行機で行くことが可能になるような最初の所持金の最小値を出力してください。
正解との絶対誤差または相対誤差が 10^{-6} 以下の場合、正答とみなされます。
入力例 1
1 3 2 10 1 2 7 2 3 9 2 2 2
出力例 1
146
最初に所持金を 146 円持っている場合、以下のようにして空港 1 から空港 3 に行くことができます。
- 航空路線 1 を使って、空港 1 から空港 2 に行く。所持金は 146 - 70 = 76 円になり、7 マイルを得る。
- 空港 2 で、7 マイルを 14 円に換金する。所持金は 76 + 14 = 90 円になる。
- 航空路線 2 を使って、空港 2 から空港 3 に行く。所持金は 90 - 90 = 0 円になり、9 マイルを得る。
最初の所持金が 146 円未満のとき、空港 1 から空港 3 に行くことはできません。
入力例 2
1 4 4 10 1 2 7 2 4 9 2 3 1 3 2 1 2 2 9 2
出力例 2
106
最初に 106 円持っている場合、以下のようにして空港 1 から空港 4 に行くことができます。
- 航空路線 1 を使って、空港 1 から空港 2 に行く。所持金は 106 - 70 = 36 円になり、7 マイルを得る。
- 航空路線 3 を使って、空港 2 から空港 3 に行く。所持金は 36 - 10 = 26 円になり、1 マイルを得る。
- 空港 3 で、8 マイルを 72 円に換金する。所持金は 26 + 72 = 98 円になる。
- 航空路線 4 を使って、空港 3 から空港 2 に行く。所持金は 98 - 10 = 88 円になり、1 マイルを得る。
- 空港 2 で、1 マイルを 2 円に換金する。所持金は 88 + 2 = 90 円になる。
- 航空路線 2 を使って、空港 2 から空港 4 に行く。所持金は 90 - 90 = 0 円になり、9 マイルを得る。
最初の所持金が 106 円未満のとき、空港 1 から空港 4 に行くことはできません。
入力例 3
1 7 8 100 3 2 81 3 4 42 1 6 97 4 5 42 4 1 59 6 3 34 5 3 68 2 7 47 0 58 37 10 89 16 0
出力例 3
16354.2758620689655172413793103448275862068965
Score : 1400 points
Problem Statement
Japan has N airports numbered 1, 2, \dots, N. AtCoder Airlines operates M directed flight routes in Japan, numbered 1, 2, \dots, M. Route j goes from airport A_j to airport B_j and costs C_j \times F yen.
Flying with AtCoder Airlines earns “miles.” You start with 0 miles. Taking route j once grants C_j miles. At airport i, you can exchange miles for money at the rate R_i yen per mile. Because of the constraint 0 \le R_i \le F-1, endless profit cycles are impossible.
You can exchange a non-integral amount of miles or have a non-integral amount of money, but you cannot have a negative amount of miles or money.
What is the minimum initial amount of money in yen needed to fly from airport 1 to airport N?
Solve \mathrm{TESTCASES} test cases.
Constraints
- 1 \le \mathrm{TESTCASES} \le 40\,000
- 2 \leq N \leq 400
- 1 \leq M \leq N \times (N-1)
- 1 \leq F \leq 100
- 1 \leq A_j \leq N
- 1 \leq B_j \leq N
- A_j \neq B_j
- (A_1, B_1), (A_2, B_2), \dots, (A_M, B_M) are all different.
- 1 \le C_j \le 100
- 0 \le R_i \le F-1
- It is possible to go from airport 1 to airport N.
- The sum of N^2 over all test cases is at most 160\,000.
- All input values are integers.
Input
The input is given from Standard Input in the following format, where \mathrm{case}_k represents the k-th test case:
\mathrm{TESTCASES}
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_{\mathrm{TESTCASES}}
Each test case is given in the following format:
N M F A_1 B_1 C_1 A_2 B_2 C_2 \vdots A_M B_M C_M R_1 R_2 \cdots R_N
Output
Print \mathrm{TESTCASES} lines. The k-th line should contain the minimum initial amount of money in yen needed to fly from airport 1 to airport N for the k-th test case.
Your output is considered as correct if its absolute or relative error is at most 10^{-6}.
Sample Input 1
1 3 2 10 1 2 7 2 3 9 2 2 2
Sample Output 1
146
If you start with 146 yen, you can go from airport 1 to airport 3:
- Take route 1 to go from airport 1 to airport 2. You now have 146-70=76 yen, and get 7 miles.
- At airport 2, exchange 7 miles for 14 yen. You now have 76+14=90 yen.
- Take route 2 to go from airport 2 to airport 3. You now have 90-90=0 yen, and get 9 miles.
If you start with less than 146 yen, you cannot go to airport 3.
Sample Input 2
1 4 4 10 1 2 7 2 4 9 2 3 1 3 2 1 2 2 9 2
Sample Output 2
106
If you start with 106 yen, you can go from airport 1 to airport 4:
- Take route 1 to go from airport 1 to airport 2. You now have 106-70=36 yen, and get 7 miles.
- Take route 3 to go from airport 2 to airport 3. You now have 36-10=26 yen, and get 1 mile.
- At airport 3, exchange 8 miles for 72 yen. You now have 26+72=98 yen.
- Take route 4 to go from airport 3 to airport 2. You now have 98-10=88 yen, and get 1 mile.
- At airport 2, exchange 1 mile for 2 yen. You now have 88+2=90 yen.
- Take route 2 to go from airport 2 to airport 4. You now have 90-90=0 yen, and get 9 miles.
If you start with less than 106 yen, you cannot go to airport 4.
Sample Input 3
1 7 8 100 3 2 81 3 4 42 1 6 97 4 5 42 4 1 59 6 3 34 5 3 68 2 7 47 0 58 37 10 89 16 0
Sample Output 3
16354.2758620689655172413793103448275862068965