実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 250 点
問題文
英小文字と ? からなる文字列 T と、英小文字のみからなる文字列 U が与えられます。
T は、英小文字のみからなる文字列 S のちょうど 4 文字を ? で置き換えることで得られた文字列です。
S が U を連続部分文字列として含んでいた可能性があるかどうか判定してください。
制約
- T は長さ 4 以上 10 以下の英小文字と
?からなる文字列 - T にはちょうど 4 つの
?が含まれる - U は長さ 1 以上 |T| 以下の英小文字からなる文字列
入力
入力は以下の形式で標準入力から与えられる。
T U
出力
S が U を部分文字列として含んでいた可能性があるならば Yes を、そうでないならば No を出力せよ。
入力例 1
tak??a?h? nashi
出力例 1
Yes
例えば、S が takanashi である場合、これは nashi を連続部分文字列として含みます。
入力例 2
??e??e snuke
出力例 2
No
? がどのような文字であっても、S は snuke を連続部分文字列として含むことがありません。
入力例 3
???? aoki
出力例 3
Yes
Score : 250 points
Problem Statement
You are given a string T consisting of lowercase English letters and ?, and a string U consisting of lowercase English letters.
The string T is obtained by taking some lowercase-only string S and replacing exactly four of its characters with ?.
Determine whether it is possible that the original string S contained U as a contiguous substring.
Constraints
- T is a string of length between 4 and 10, inclusive, consisting of lowercase letters and
?. - T contains exactly four occurrences of
?. - U is a string of length between 1 and |T|, inclusive, consisting of lowercase letters.
Input
The input is given from Standard Input in the following format:
T U
Output
Print Yes if it is possible that the original string S contained U as a contiguous substring; otherwise, print No.
Sample Input 1
tak??a?h? nashi
Sample Output 1
Yes
For example, if S is takanashi, it contains nashi as a contiguous substring.
Sample Input 2
??e??e snuke
Sample Output 2
No
No matter what characters replace the ?s in T, S cannot contain snuke as a contiguous substring.
Sample Input 3
???? aoki
Sample Output 3
Yes
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
1 から N の番号がついた N 人の人がいます。
人 i はキーエンス本社ビルの建築面積を S_i 平方メートルであると予想しました。
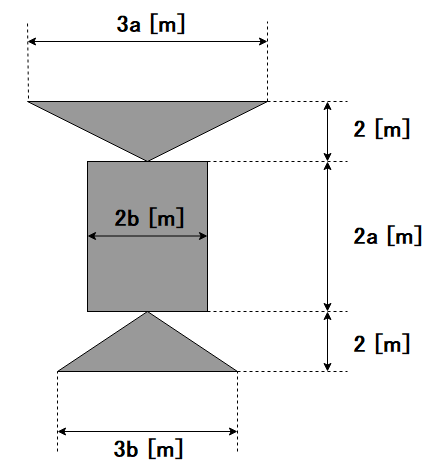
キーエンス本社ビルは下図のような形をしています。ただし、a,b はある 正の整数 です。
つまり、キーエンス本社ビルの建築面積は 4ab+3a+3b 平方メートルと表されます。
N 人のうち、この情報のみによって、予想した面積が確実に誤りであるとわかる人数を求めてください。
制約
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N S_1 \ldots S_N
出力
答えを出力せよ。
入力例 1
3 10 20 39
出力例 1
1
a=1,b=1 のとき面積は 10 平方メートル、a=2,b=3 のとき面積は 39 平方メートルとなります。
しかし a,b がどのような正の整数であったとしても面積が 20 平方メートルになることはありません。
よって、人 2 の予想だけは確実に誤りであることがわかります。
入力例 2
5 666 777 888 777 666
出力例 2
3
Score : 200 points
Problem Statement
There are N people numbered 1 to N.
Person i guessed the building area of KEYENCE headquarters building to be S_i square meters.
The shape of KEYENCE headquarters building is shown below, where a and b are some positive integers.
That is, the building area of the building can be represented as 4ab+3a+3b.
Based on just this information, how many of the N people are guaranteed to be wrong in their guesses?

Constraints
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N S_1 \ldots S_N
Output
Print the answer.
Sample Input 1
3 10 20 39
Sample Output 1
1
The area would be 10 square meters if a=1,b=1, and 39 square meters if a=2,b=3.
However, no pair of positive integers a and b would make the area 20 square meters.
Thus, we can only be sure that Person 2 guessed wrong.
Sample Input 2
5 666 777 888 777 666
Sample Output 2
3
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
英小文字からなる 2 つの文字列 S, T が与えられます。 次の操作を好きな回数( 0 回でも良い)行うことで、S を T と一致させることができるかを判定してください。
S において同じ文字が 2 文字連続しているところの間に、その文字と同じ文字を 1 つ挿入する。 すなわち、下記の 3 つの手順からなる操作を行う。
- 現在の S の長さを N とし、S = S_1S_2\ldots S_N とする。
- 1 以上 N-1 以下の整数 i であって、S_i = S_{i+1} を満たすものを 1 つ選択する。(ただし、そのような i が存在しない場合は、何もせずに手順 3.をスキップして操作を終了する。)
- S の i 文字目と i+1 文字目の間に文字 S_i(= S_{i+1}) を 1 つ挿入する。その結果、S は長さ N+1 の文字列 S_1S_2\ldots S_i S_i S_{i+1} \ldots S_N となる。
制約
- S と T はそれぞれ英小文字からなる長さ 2 以上 2 \times 10^5 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
S T
出力
S を T と一致させることができる場合は Yes を、そうでない場合は No を出力せよ。
ジャッジは英小文字と英大文字を厳密に区別することに注意せよ。
入力例 1
abbaac abbbbaaac
出力例 1
Yes
下記の 3 回の操作によって、S = abbaac を T = abbbbaaac に一致させることができます。
- まず、S の 2 文字目と 3 文字目の間に
bを挿入する。その結果、S =abbbaacとなる。 - 次に、再び S の 2 文字目と 3 文字目の間に
bを挿入する。その結果、S =abbbbaacとなる。 - 最後に、S の 6 文字目と 7 文字目の間に
aを挿入する。その結果、S =abbbbaaacとなる。
よって、Yes を出力します。
入力例 2
xyzz xyyzz
出力例 2
No
どのように操作を行っても、 S = xyzz を T = xyyzz に一致させることはできません。
よって、No を出力します。
Score : 300 points
Problem Statement
You are given two strings S and T. Determine whether it is possible to make S equal T by performing the following operation some number of times (possibly zero).
Between two consecutive equal characters in S, insert a character equal to these characters. That is, take the following three steps.
- Let N be the current length of S, and S = S_1S_2\ldots S_N.
- Choose an integer i between 1 and N-1 (inclusive) such that S_i = S_{i+1}. (If there is no such i, do nothing and terminate the operation now, skipping step 3.)
- Insert a single copy of the character S_i(= S_{i+1}) between the i-th and (i+1)-th characters of S. Now, S is a string of length N+1: S_1S_2\ldots S_i S_i S_{i+1} \ldots S_N.
Constraints
- Each of S and T is a string of length between 2 and 2 \times 10^5 (inclusive) consisting of lowercase English letters.
Input
Input is given from Standard Input in the following format:
S T
Output
If it is possible to make S equal T, print Yes; otherwise, print No.
Note that the judge is case-sensitive.
Sample Input 1
abbaac abbbbaaac
Sample Output 1
Yes
You can make S = abbaac equal T = abbbbaaac by the following three operations.
- First, insert
bbetween the 2-nd and 3-rd characters of S. Now, S =abbbaac. - Next, insert
bagain between the 2-nd and 3-rd characters of S. Now, S =abbbbaac. - Lastly, insert
abetween the 6-th and 7-th characters of S. Now, S =abbbbaaac.
Thus, Yes should be printed.
Sample Input 2
xyzz xyyzz
Sample Output 2
No
No sequence of operations makes S = xyzz equal T = xyyzz.
Thus, No should be printed.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
英小文字からなる長さ N の文字列 S が与えられます。
S の空でない部分文字列であって、1 種類の文字のみからなるものの数を求めてください。 ただし、文字列として等しい部分文字列同士は、取り出し方が異なっても区別しません。
なお、S の空でない部分文字列とは、S の先頭から 0 文字以上、末尾から 0 文字以上削除して得られる文字列のうち、長さが 1 以上であるもののことをいいます。
例えば、ab や abc は abc の空でない部分文字列ですが、ac や空文字列は abc の空でない部分文字列ではありません。
制約
- 1 \leq N \leq 2\times 10^5
- S は英小文字からなる長さ N の文字列
入力
入力は以下の形式で標準入力から与えられる。
N S
出力
S の空でない部分文字列であって、1 種類の文字のみからなるものの数を出力せよ。
入力例 1
6 aaabaa
出力例 1
4
S の空でない部分文字列であって、1 種類の文字のみからなるものは a, aa, aaa, b の 4 つです。
S から a や aa を取り出す方法は 1 通りではありませんが、それぞれ 1 回ずつしか数えないことに注意してください。
入力例 2
1 x
出力例 2
1
入力例 3
12 ssskkyskkkky
出力例 3
8
Score : 300 points
Problem Statement
You are given a string S of length N consisting of lowercase English letters.
Find the number of non-empty substrings of S that are repetitions of one character. Here, two substrings that are equal as strings are not distinguished even if they are obtained differently.
A non-empty substring of S is a string of length at least one obtained by deleting zero or more characters from the beginning and zero or more characters from the end of S. For example, ab and abc are non-empty substrings of abc, while ac and the empty string are not.
Constraints
- 1 \leq N \leq 2\times 10^5
- S is a string of length N consisting of lowercase English letters.
Input
The input is given from Standard Input in the following format:
N S
Output
Print the number of non-empty substrings of S that are repetitions of one character.
Sample Input 1
6 aaabaa
Sample Output 1
4
The non-empty substrings of S that are repetitions of one character are a, aa, aaa, and b; there are four of them. Note that there are multiple ways to obtain a or aa from S, but each should only be counted once.
Sample Input 2
1 x
Sample Output 2
1
Sample Input 3
12 ssskkyskkkky
Sample Output 3
8
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
H 行 W 列のグリッドがあります。上から i 行目、左から j 列目のマスをマス (i, j) と呼びます。
各マスには o 、x 、. のうちいずれかの文字が書かれています。
各マスに書かれた文字は H 個の長さ W の文字列 S_1, S_2, \ldots, S_H で表され、
マス (i, j) に書かれた文字は、文字列 S_i の j 文字目と一致します。
このグリッドに対して、下記の操作を 0 回以上好きな回数だけ繰り返します。
.が書かれているマスを 1 個選び、そのマスに書かれた文字をoに変更する。
その結果、縦方向または横方向に連続した K 個のマスであってそれらに書かれた文字がすべて o であるようなものが存在する(
すなわち、下記の 2 つの条件のうち少なくとも一方を満たす)ようにすることが可能かを判定し、可能な場合はそのために行う操作回数の最小値を出力してください。
- 1 \leq i \leq H かつ 1 \leq j \leq W-K+1 を満たす整数の組 (i, j) であって、マス (i, j), (i, j+1), \ldots, (i, j+K-1) に書かれた文字が
oであるものが存在する。 - 1 \leq i \leq H-K+1 かつ 1 \leq j \leq W を満たす整数の組 (i, j) であって、マス (i, j), (i+1, j), \ldots, (i+K-1, j) に書かれた文字が
oであるものが存在する。
制約
- H, W, K は整数
- 1 \leq H
- 1 \leq W
- H \times W \leq 2 \times 10^5
- 1 \leq K \leq \max\lbrace H, W \rbrace
- S_i は
o、x、.のみからなる長さ W の文字列
入力
入力は以下の形式で標準入力から与えられる。
H W K S_1 S_2 \vdots S_H
出力
問題文中の条件を満たすことが不可能な場合は -1 を、可能な場合はそのために行う操作回数の最小値を出力せよ。
入力例 1
3 4 3 xo.x ..o. xx.o
出力例 1
2
操作を 2 回行って、例えばマス (2, 1) とマス (2, 2) に書かれた文字をそれぞれ o に変更することで問題文中の条件を満たすことができ、これが最小の操作回数です。
入力例 2
4 2 3 .o .o .o .o
出力例 2
0
操作を一度も行わなくても問題文中の条件を満たします。
入力例 3
3 3 3 x.. ..x .x.
出力例 3
-1
問題文中の条件を満たすことは不可能なので、-1 を出力します。
入力例 4
10 12 6 ......xo.o.. x...x.....o. x........... ..o...x..... .....oo..... o.........x. ox.oox.xx..x ....o...oox. ..o.....x.x. ...o........
出力例 4
3
Score: 400 points
Problem Statement
There is a grid with H rows and W columns. Let (i, j) denote the cell at the i-th row from the top and the j-th column from the left.
Each cell contains one of the characters o, x, and .. The characters written in each cell are represented by H strings S_1, S_2, \ldots, S_H of length W; the character written in cell (i, j) is the j-th character of the string S_i.
For this grid, you may repeat the following operation any number of times, possibly zero:
- Choose one cell with the character
.and change the character in that cell too.
Determine if it is possible to have a sequence of K horizontally or vertically consecutive cells with o written in all cells (in other words, satisfy at least one of the following two conditions). If it is possible, print the minimum number of operations required to achieve this.
- There is an integer pair (i, j) satisfying 1 \leq i \leq H and 1 \leq j \leq W-K+1 such that the characters in cells (i, j), (i, j+1), \ldots, (i, j+K-1) are all
o. - There is an integer pair (i, j) satisfying 1 \leq i \leq H-K+1 and 1 \leq j \leq W such that the characters in cells (i, j), (i+1, j), \ldots, (i+K-1, j) are all
o.
Constraints
- H, W, and K are integers.
- 1 \leq H
- 1 \leq W
- H \times W \leq 2 \times 10^5
- 1 \leq K \leq \max\lbrace H, W \rbrace
- S_i is a string of length W consisting of the characters
o,x, and..
Input
The input is given from Standard Input in the following format:
H W K S_1 S_2 \vdots S_H
Output
If it is impossible to satisfy the condition in the problem statement, print -1. Otherwise, print the minimum number of operations required to do so.
Sample Input 1
3 4 3 xo.x ..o. xx.o
Sample Output 1
2
By operating twice, for example, changing the characters in cells (2, 1) and (2, 2) to o, you can satisfy the condition in the problem statement, and this is the minimum number of operations required.
Sample Input 2
4 2 3 .o .o .o .o
Sample Output 2
0
The condition is satisfied without performing any operations.
Sample Input 3
3 3 3 x.. ..x .x.
Sample Output 3
-1
It is impossible to satisfy the condition, so print -1.
Sample Input 4
10 12 6 ......xo.o.. x...x.....o. x........... ..o...x..... .....oo..... o.........x. ox.oox.xx..x ....o...oox. ..o.....x.x. ...o........
Sample Output 4
3