Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 350 点
問題文
正の整数 X は、次の条件をみたすときかつその時に限り、良い整数と呼ばれます。
- 正の整数の組 (a,b) を用いて、X=2^a\times b^2 と書ける。
例えば、400 は 400=2^2\times 10^2 と書けるため、良い整数です。
正の整数 N が与えられるので、1 以上 N 以下の良い整数の個数を求めてください。
制約
- 1 \leq N \leq 10^{18}
- N は整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
1 以上 N 以下の良い整数の個数を出力せよ。
入力例 1
20
出力例 1
5
1 以上 20 以下の良い整数は 2,4,8,16,18 の 5 つです。
よって、5 を出力します。
入力例 2
400
出力例 2
24
入力例 3
1234567890
出力例 3
42413
入力が 32bit 整数型に収まるとは限らないことに注意してください。
Score : 350 points
Problem Statement
A positive integer X is called a good integer if and only if it satisfies the following condition:
- There exists a pair of positive integers (a,b) such that X = 2^a \times b^2.
For example, 400 is a good integer because 400 = 2^2 \times 10^2.
Given a positive integer N, find the number of good integers between 1 and N, inclusive.
Constraints
- 1 \leq N \leq 10^{18}
- N is an integer.
Input
The input is given from Standard Input in the following format:
N
Output
Print the number of good integers between 1 and N, inclusive.
Sample Input 1
20
Sample Output 1
5
There are five good integers between 1 and 20: 2, 4, 8, 16, and 18.
Thus, print 5.
Sample Input 2
400
Sample Output 2
24
Sample Input 3
1234567890
Sample Output 3
42413
Note that the input might not fit in a 32-bit integer type.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
2 次元グリッド上に 2 つの図形 S と T があります。グリッドは正方形のマスからなります。
S は N 行 N 列のグリッド内にあり、S_{i,j} が # であるようなマス全体からなります。
T も N 行 N 列のグリッド内にあり、T_{i,j} が # であるようなマス全体からなります。
S と T を 90 度回転及び平行移動の繰り返しによって一致させることができるか判定してください。
制約
- 1 \leq N \leq 200
- S,T は
#と.のみからなる - S,T は 1 つ以上
#を含む
入力
入力は以下の形式で標準入力から与えられる。
N
S_{1,1}S_{1,2}\ldots S_{1,N}
\vdots
S_{N,1}S_{N,2}\ldots S_{N,N}
T_{1,1}T_{1,2}\ldots T_{1,N}
\vdots
T_{N,1}T_{N,2}\ldots T_{N,N}
出力
S と T を90 度回転及び平行移動の繰り返しによって一致させることができるとき Yes を、そうでないとき No を出力せよ。
入力例 1
5 ..... ..#.. .###. ..... ..... ..... ..... ....# ...## ....#
出力例 1
Yes
S を左回りに 90 度回転させ、平行移動することで T に一致させることができます。
入力例 2
5 ##### ##..# #..## ##### ..... ##### #..## ##..# ##### .....
出力例 2
No
90 度回転と平行移動の繰り返しによって一致させることはできません。
入力例 3
4 #... ..#. ..#. .... #... #... ..#. ....
出力例 3
Yes
S 及び T は連結とは限りません。
入力例 4
4 #... .##. ..#. .... ##.. #... ..#. ....
出力例 4
No
回転や移動の操作は連結成分ごとにできるわけではなく、S,T 全体に対して行うことに注意してください。
Score : 300 points
Problem Statement
We have two figures S and T on a two-dimensional grid with square cells.
S lies within a grid with N rows and N columns, and consists of the cells where S_{i,j} is #.
T lies within the same grid with N rows and N columns, and consists of the cells where T_{i,j} is #.
Determine whether it is possible to exactly match S and T by 90-degree rotations and translations.
Constraints
- 1 \leq N \leq 200
- Each of S and T consists of
#and.. - Each of S and T contains at least one
#.
Input
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}\ldots S_{1,N}
\vdots
S_{N,1}S_{N,2}\ldots S_{N,N}
T_{1,1}T_{1,2}\ldots T_{1,N}
\vdots
T_{N,1}T_{N,2}\ldots T_{N,N}
Output
Print Yes if it is possible to exactly match S and T by 90-degree rotations and translations, and No otherwise.
Sample Input 1
5 ..... ..#.. .###. ..... ..... ..... ..... ....# ...## ....#
Sample Output 1
Yes
We can match S to T by rotating it 90-degrees counter-clockwise and translating it.
Sample Input 2
5 ##### ##..# #..## ##### ..... ##### #..## ##..# ##### .....
Sample Output 2
No
It is impossible to match them by 90-degree rotations and translations.
Sample Input 3
4 #... ..#. ..#. .... #... #... ..#. ....
Sample Output 3
Yes
Each of S and T may not be connected.
Sample Input 4
4 #... .##. ..#. .... ##.. #... ..#. ....
Sample Output 4
No
Note that it is not allowed to rotate or translate just a part of a figure; it is only allowed to rotate or translate a whole figure.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
10^9 行 W 列のグリッドがあります。左から x 列目、下から y 行目のマスを (x,y) と表します。
N 個のブロックがあります。各ブロックは 1 \times 1 の正方形で、ブロック i (1 \leq i \leq N) は時刻 0 にマス (X_i,Y_i) にあります。
時刻 t=1,2,\dots,10^{100} に、以下のルールに従ってブロックを動かします。
- グリッドの下から 1 行目がすべてブロックで埋まっているならば、下から 1 行目にあるブロックをすべて消滅させる。
- 残っているブロックについて、下にあるブロックから順番に、以下の操作を行う。
- ブロックが一番下の行にある、またはそのブロックの 1 つ下のマスにもブロックがあるならば、何もしない
- そうでなければ、ブロックを 1 つ下のマスに動かす。
Q 個の質問が与えられます。j 番目 (1 \leq j \leq Q) の質問では、時刻 T_j+0.5 にブロック A_j が存在するかどうか答えてください。
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq W \leq N
- 1 \leq X_i \leq W
- 1 \leq Y_i \leq 10^9
- i \neq j なら (X_i,Y_i) \neq (X_j,Y_j)
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_j \leq 10^9
- 1 \leq A_j \leq N
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N Q T_1 A_1 T_2 A_2 \vdots T_Q A_Q
出力
Q 行出力せよ。i 行目には、時刻 T_i+0.5 にブロック A_i が存在するならば Yes を、存在しないならば No を出力せよ。
入力例 1
5 3 1 1 1 2 2 2 3 2 2 3 6 1 1 1 2 2 3 2 5 3 4 3 5
出力例 1
Yes Yes No Yes No Yes
ブロックの位置は以下のように変化します。
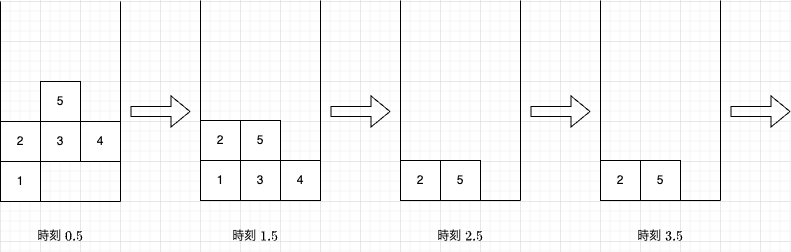
- 質問 1: 時刻 1.5 にブロック 1 は存在するので、答えは
Yesです。 - 質問 2: 時刻 1.5 にブロック 2 は存在するので、答えは
Yesです。 - 質問 3: ブロック 3 は時刻 2 に消滅します。よって、時刻 2.5 にブロック 3 は存在しないので、答えは
Noです。
入力例 2
3 2 1 1 2 1 1 2 4 1 1 1 2 1 3 2 3
出力例 2
No No Yes Yes
Score : 400 points
Problem Statement
There is a grid with 10^9 rows and W columns. The cell at the x-th column from the left and the y-th row from the bottom is denoted by (x,y).
There are N blocks. Each block is a 1 \times 1 square, and block i-th (1 \leq i \leq N) is located at cell (X_i,Y_i) at time 0.
At times t=1,2,\dots,10^{100}, the blocks are moved according to the following rules:
- If the entire bottom row is filled with blocks, then all blocks in the bottom row are removed.
- For each remaining block, in order from bottom to top, perform the following:
- If the block is in the bottom row, or if there is a block in the cell immediately below it, do nothing.
- Otherwise, move the block one cell downward.
You are given Q queries. For the j-th query (1 \leq j \leq Q), answer whether block A_j exists at time T_j+0.5.
Constraints
- 1 \leq N \leq 2 \times 10^5
- 1 \leq W \leq N
- 1 \leq X_i \leq W
- 1 \leq Y_i \leq 10^9
- (X_i,Y_i) \neq (X_j,Y_j) if i \neq j.
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq T_j \leq 10^9
- 1 \leq A_j \leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N W X_1 Y_1 X_2 Y_2 \vdots X_N Y_N Q T_1 A_1 T_2 A_2 \vdots T_Q A_Q
Output
Print Q lines. The i-th line should contain Yes if block A_i exists at time T_i+0.5, and No otherwise.
Sample Input 1
5 3 1 1 1 2 2 2 3 2 2 3 6 1 1 1 2 2 3 2 5 3 4 3 5
Sample Output 1
Yes Yes No Yes No Yes
The positions of the blocks change as follows: ("時刻" means "time.")

- Query 1: At time 1.5, block 1 exists, so the answer is
Yes. - Query 2: At time 1.5, block 2 exists, so the answer is
Yes. - Query 3: Block 3 disappears at time 2, so it does not exist at time 2.5, and the answer is
No.
Sample Input 2
3 2 1 1 2 1 1 2 4 1 1 1 2 1 3 2 3
Sample Output 2
No No Yes Yes
Time Limit: 4 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
高橋君は N 枚のチョコレートを持っています。i 枚目のチョコレートは縦 A_i cm 横 B_i cm の長方形の形をしています。
また、高橋君は M 個の箱を持っています。i 個目の箱は縦 C_i cm 横 D_i cm の長方形の形をしています。
以下の条件を全て満たすように N 枚のチョコレートを全て箱に入れることは可能か判定してください。
- 1 個の箱に入れることのできるチョコレートの数は、高々 1 個である
- i 枚目のチョコレートを j 個目の箱に入れるとき、A_i \leq C_j かつ B_i \leq D_j を満たす必要がある(回転は不可)
制約
- 1 \leq N \leq M \leq 2\times 10^5
- 1 \leq A_i,B_i,C_i,D_i \leq 10^9
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 \ldots A_N B_1 \ldots B_N C_1 \ldots C_M D_1 \ldots D_M
出力
N 枚のチョコレートを全て箱に入れることが可能ならば Yes と、不可能ならば No と出力せよ。
入力例 1
2 3 2 4 3 2 8 1 5 2 10 5
出力例 1
Yes
1 枚目のチョコレートを 3 個目の箱に入れて、2 枚目のチョコレートを 1 個目の箱に入れればよいです。
入力例 2
2 2 1 1 2 2 100 1 100 1
出力例 2
No
1 個の箱に入れることのできるチョコレートの数は、高々 1 個です。
入力例 3
1 1 10 100 100 10
出力例 3
No
入力例 4
1 1 10 100 10 100
出力例 4
Yes
Score : 500 points
Problem Statement
Takahashi has N pieces of chocolate. The i-th piece has a rectangular shape with a width of A_i centimeters and a length of B_i centimeters.
He also has M boxes. The i-th box has a rectangular shape with a width of C_i centimeters and a length of D_i centimeters.
Determine whether it is possible to put the N pieces of chocolate in the boxes under the conditions below.
- A box can contain at most one piece of chocolate.
- A_i \leq C_j and B_i \leq D_j must hold when putting the i-th piece of chocolate in the j-th box (they cannot be rotated).
Constraints
- 1 \leq N \leq M \leq 2\times 10^5
- 1 \leq A_i,B_i,C_i,D_i \leq 10^9
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N M A_1 \ldots A_N B_1 \ldots B_N C_1 \ldots C_M D_1 \ldots D_M
Output
If it is possible to put the N pieces of chocolate in the boxes, print Yes; otherwise, print No.
Sample Input 1
2 3 2 4 3 2 8 1 5 2 10 5
Sample Output 1
Yes
We can put the first piece of chocolate in the third box and the second piece in the first box.
Sample Input 2
2 2 1 1 2 2 100 1 100 1
Sample Output 2
No
A box can contain at most one piece of chocolate.
Sample Input 3
1 1 10 100 100 10
Sample Output 3
No
Sample Input 4
1 1 10 100 10 100
Sample Output 4
Yes
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
高橋君と青木君が、数の書かれたカードを使ってゲームをします。
最初、高橋君は A_1,\ldots,A_N が書かれた N 枚のカードを、青木君は B_1,\ldots,B_M が書かれた M 枚のカードを手札として持っており、場には C_1,\ldots,C_L が書かれた L 枚のカードがあります。
高橋君と青木君はゲーム中常に、相手の手札も含め、全てのカードに書かれた数を知っている状態にあります。
高橋君と青木君は、高橋君から順に次の行動を交互に行います。
- 自分の手札から 1 枚選び場に出す。その後、出したカードに書かれていた数未満の数が書かれたカードが場にあれば、そのうち 1 枚を場から自分の手札に移して良い。
先に行動が行えなくなった方が負けであり、負けでない方が勝ちです。互いに最適に行動したとき、どちらが勝つか判定してください。
なおこのゲームは必ず有限回の行動で勝敗がつくことが証明できます。
制約
- 1 \leq N,M,L
- N+M+L \leq 12
- 1 \leq A_i,B_i,C_i \leq 10^9
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M L A_1 \ldots A_N B_1 \ldots B_M C_1 \ldots C_L
出力
高橋君が勝つならば Takahashi、青木君が勝つならば Aoki と出力せよ。
入力例 1
1 1 2 2 4 1 3
出力例 1
Aoki
ゲームは例えば次のように進行します。(最適な行動とは限りません)
- 高橋君が手札から 2 を場に出し、1 を場から自分の手札に移す。高橋君の手札は (1)、青木君の手札は (4)、場札は (2,3) となる。
- 青木君が手札から 4 を場に出し、2 を場から自分の手札に移す。高橋君の手札は (1)、青木君の手札は (2)、場札は (3,4) となる。
- 高橋君が手札から 1 を場に出す。高橋君の手札は ()、青木君の手札は (2)、場札は (1,3,4) となる。
- 青木君が手札から 2 を場に出す。高橋君の手札は ()、青木君の手札は ()、場札は (1,2,3,4) となる。
- 高橋君は行動できないため負けであり、青木君が勝ち。
入力例 2
4 4 4 98 98765 987654 987654321 987 9876 9876543 98765432 123 12345 1234567 123456789
出力例 2
Takahashi
入力例 3
1 1 8 10 10 1 2 3 4 5 6 7 8
出力例 3
Aoki
Score : 500 points
Problem Statement
Takahashi and Aoki will play a game using cards with numbers written on them.
Initially, Takahashi has N cards with numbers A_1, \ldots, A_N in his hand, Aoki has M cards with numbers B_1, \ldots, B_M in his hand, and there are L cards with numbers C_1, \ldots, C_L on the table.
Throughout the game, both Takahashi and Aoki know all the numbers on all the cards, including the opponent's hand.
Starting with Takahashi, they take turns performing the following action:
- Choose one card from his hand and put it on the table. Then, if there is a card on the table with a number less than the number on the card he just played, he may take one such card from the table into his hand.
The player who cannot make a move first loses, and the other player wins. Determine who wins if both players play optimally.
It can be proved that the game always ends in a finite number of moves.
Constraints
- 1 \leq N, M, L
- N + M + L \leq 12
- 1 \leq A_i, B_i, C_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M L A_1 \ldots A_N B_1 \ldots B_M C_1 \ldots C_L
Output
Print Takahashi if Takahashi wins, and Aoki if Aoki wins.
Sample Input 1
1 1 2 2 4 1 3
Sample Output 1
Aoki
The game may proceed as follows (not necessarily optimal moves):
- Takahashi plays 2 from his hand to the table, and takes 1 from the table into his hand. Now, Takahashi's hand is (1), Aoki's hand is (4), and the table cards are (2,3).
- Aoki plays 4 from his hand to the table, and takes 2 into his hand. Now, Takahashi's hand is (1), Aoki's hand is (2), and the table cards are (3,4).
- Takahashi plays 1 from his hand to the table. Now, Takahashi's hand is (), Aoki's hand is (2), and the table cards are (1,3,4).
- Aoki plays 2 from his hand to the table. Now, Takahashi's hand is (), Aoki's hand is (), and the table cards are (1,2,3,4).
- Takahashi cannot make a move and loses; Aoki wins.
Sample Input 2
4 4 4 98 98765 987654 987654321 987 9876 9876543 98765432 123 12345 1234567 123456789
Sample Output 2
Takahashi
Sample Input 3
1 1 8 10 10 1 2 3 4 5 6 7 8
Sample Output 3
Aoki