実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
1 以上 N 以下の整数からなる集合が M 個あり、順に S_1, S_2, \dots, S_M と呼びます。
S_i は C_i 個の整数 a_{i, 1}, a_{i, 2}, \dots, a_{i, C_i} からなります。
M 個の集合から 1 個以上の集合を選ぶ方法は 2^M-1 通りあります。
このうち、次の条件を満たす選び方は何通りありますか?
- 1 \leq x \leq N を満たす全ての整数 x に対して、選んだ集合の中に x を含む集合が少なくとも 1 個存在する。
制約
- 1 \leq N \leq 10
- 1 \leq M \leq 10
- 1 \leq C_i \leq N
- 1 \leq a_{i,1} \lt a_{i,2} \lt \dots \lt a_{i,C_i} \leq N
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M
C_1
a_{1,1} a_{1,2} \dots a_{1,C_1}
C_2
a_{2,1} a_{2,2} \dots a_{2,C_2}
\vdots
C_M
a_{M,1} a_{M,2} \dots a_{M,C_M}
出力
問題文の条件を満たす集合の選び方の数を出力せよ。
入力例 1
3 3 2 1 2 2 1 3 1 2
出力例 1
3
入力で与えられている集合はそれぞれ S_1 = \lbrace 1, 2 \rbrace, S_2 = \lbrace 1, 3 \rbrace, S_3 = \lbrace 2 \rbrace です。
問題文の条件を満たす集合の選び方は次の 3 通りです。
- S_1, S_2 を選ぶ。
- S_1, S_2, S_3 を選ぶ。
- S_2, S_3 を選ぶ。
入力例 2
4 2 2 1 2 2 1 3
出力例 2
0
問題文の条件を満たす選び方が存在しない場合もあります。
入力例 3
6 6 3 2 3 6 3 2 4 6 2 3 6 3 1 5 6 3 1 3 6 2 1 4
出力例 3
18
Score : 300 points
Problem Statement
There are M sets, called S_1, S_2, \dots, S_M, consisting of integers between 1 and N.
S_i consists of C_i integers a_{i, 1}, a_{i, 2}, \dots, a_{i, C_i}.
There are (2^M-1) ways to choose one or more sets from the M sets.
How many of them satisfy the following condition?
- For all integers x such that 1 \leq x \leq N, there is at least one chosen set containing x.
Constraints
- 1 \leq N \leq 10
- 1 \leq M \leq 10
- 1 \leq C_i \leq N
- 1 \leq a_{i,1} \lt a_{i,2} \lt \dots \lt a_{i,C_i} \leq N
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N M
C_1
a_{1,1} a_{1,2} \dots a_{1,C_1}
C_2
a_{2,1} a_{2,2} \dots a_{2,C_2}
\vdots
C_M
a_{M,1} a_{M,2} \dots a_{M,C_M}
Output
Print the number of ways to choose sets that satisfy the conditions in the Problem Statement.
Sample Input 1
3 3 2 1 2 2 1 3 1 2
Sample Output 1
3
The sets given in the input are S_1 = \lbrace 1, 2 \rbrace, S_2 = \lbrace 1, 3 \rbrace, S_3 = \lbrace 2 \rbrace.
The following three ways satisfy the conditions in the Problem Statement:
- choosing S_1, S_2;
- choosing S_1, S_2, S_3;
- choosing S_2, S_3.
Sample Input 2
4 2 2 1 2 2 1 3
Sample Output 2
0
There may be no way to choose sets that satisfies the conditions in the Problem Statement.
Sample Input 3
6 6 3 2 3 6 3 2 4 6 2 3 6 3 1 5 6 3 1 3 6 2 1 4
Sample Output 3
18
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
ある地方に、1 から N の番号がついた N 個の街と、1 から M の番号がついた M 本の道路があります。
i 番目の道路は街 A_i と街 B_i を双方向に結び、長さは C_i です。
好きな街からスタートして同じ街を二度以上通らずに別の街へ移動するときの、通る道路の長さの和としてありえる最大値を求めてください。
制約
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1\leq A_i < B_i \leq N
- (A_i,B_i) は相異なる
- 1\leq C_i \leq 10^8
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 C_1 \vdots A_M B_M C_M
出力
答えを出力せよ。
入力例 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
出力例 1
1110
4\to 1\to 3\to 2 と移動すると、通る道路の長さの和は 1110 となります。
入力例 2
10 1 5 9 1
出力例 2
1
道路と繋がっていない街が存在するかもしれません。
入力例 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
出力例 3
20
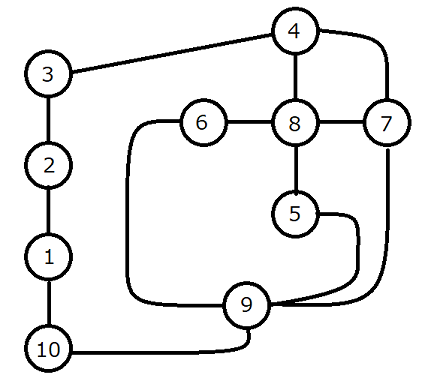
Score : 300 points
Problem Statement
A region has N towns numbered 1 to N, and M roads numbered 1 to M.
The i-th road connects town A_i and town B_i bidirectionally with length C_i.
Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.
Constraints
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1 \leq A_i < B_i \leq N
- The pairs (A_i,B_i) are distinct.
- 1\leq C_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 C_1 \vdots A_M B_M C_M
Output
Print the answer.
Sample Input 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
Sample Output 1
1110
If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.
Sample Input 2
10 1 5 9 1
Sample Output 2
1
There may be a town that is not connected to a road.
Sample Input 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
Sample Output 3
20

実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
N = 2^{20} 項からなる数列 A = (A_0, A_1, \dots, A_{N - 1}) があります。はじめ、全ての要素は -1 です。
Q 個のクエリを順番に処理してください。i \, (1 \leq i \leq Q) 個目のクエリは t_i = 1 または t_i = 2 を満たす整数 t_i および整数 x_i で表され、内容は以下の通りです。
- t_i = 1 のとき、以下の処理を順番に行う。
- 整数 h を h = x_i で定める。
- A_{h \bmod N} \neq -1 である間、h の値を 1 増やすことを繰り返す。この問題の制約下でこの操作が有限回で終了することは証明できる。
- A_{h \bmod N} の値を x_i で書き換える。
- t_i = 2 のとき、その時点での A_{x_i \bmod N} の値を出力する。
なお、整数 a, b に対し、a を b で割った余りを a \bmod b と表します。
制約
- 1 \leq Q \leq 2 \times 10^5
- t_i \in \{ 1, 2 \} \, (1 \leq i \leq Q)
- 0 \leq x_i \leq 10^{18} \, (1 \leq i \leq Q)
- t_i = 2 であるような i \, (1 \leq i \leq Q) が 1 つ以上存在する。
- 入力は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
Q
t_1 x_1
\vdots
t_{Q} x_{Q}
出力
t_i = 2 であるようなクエリに対し、それぞれ答えを 1 行に出力せよ。そのようなクエリが 1 つ以上存在することは保証される。
入力例 1
4 1 1048577 1 1 2 2097153 2 3
出力例 1
1048577 -1
x_1 \bmod N = 1 であるので、1 番目のクエリによって A_1 = 1048577 となります。
2 番目のクエリにおいて、はじめ h = x_2 ですが、A_{h \bmod N} = A_{1} \neq -1 であるので h の値を 1 増やします。すると A_{h \bmod N} = A_{2} = -1 となるので、このクエリによって A_2 = 1 となります。
3 番目のクエリにおいて、A_{x_3 \bmod N} = A_{1} = 1048577 を出力します。
4 番目のクエリにおいて、A_{x_4 \bmod N} = A_{3} = -1 を出力します。
この問題において N = 2^{20} = 1048576 は定数であり、入力では与えられないことに注意してください。
Score : 400 points
Problem Statement
There is a sequence A = (A_0, A_1, \dots, A_{N - 1}) with N = 2^{20} terms. Initially, every term is -1.
Process Q queries in order. The i-th query (1 \leq i \leq Q) is described by an integer t_i such that t_i = 1 or t_i = 2, and another integer x_i, as follows.
- If t_i = 1, do the following in order.
- Define an integer h as h = x_i.
- While A_{h \bmod N} \neq -1, keep adding 1 to h. We can prove that this process ends after finite iterations under the Constraints of this problem.
- Replace the value of A_{h \bmod N} with x_i.
- If t_i = 2, print the value of A_{x_i \bmod N} at that time.
Here, for integers a and b, a \bmod b denotes the remainder when a is divided by b.
Constraints
- 1 \leq Q \leq 2 \times 10^5
- t_i \in \{ 1, 2 \} \, (1 \leq i \leq Q)
- 0 \leq x_i \leq 10^{18} \, (1 \leq i \leq Q)
- There is at least one i (1 \leq i \leq Q) such that t_i = 2.
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
Q
t_1 x_1
\vdots
t_{Q} x_{Q}
Output
For each query with t_i = 2, print the response in one line. It is guaranteed that there is at least one such query.
Sample Input 1
4 1 1048577 1 1 2 2097153 2 3
Sample Output 1
1048577 -1
We have x_1 \bmod N = 1, so the first query sets A_1 = 1048577.
In the second query, initially we have h = x_2, for which A_{h \bmod N} = A_{1} \neq -1, so we add 1 to h. Now we have A_{h \bmod N} = A_{2} = -1, so this query sets A_2 = 1.
In the third query, we print A_{x_3 \bmod N} = A_{1} = 1048577.
In the fourth query, we print A_{x_4 \bmod N} = A_{3} = -1.
Note that, in this problem, N = 2^{20} = 1048576 is a constant and not given in input.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 475 点
問題文
高橋君と青木君は N 枚のカードを使ってとあるゲームをします。i 枚目のカードの表面には A_i が、裏面には B_i が書かれています。初めに場には N 枚のカードが並べられており、高橋君を先手として、2 人は以下の操作を交互に繰り返します。
- 場にあるカードの中から表面同士に同じ数が書かれている、または裏面同士に同じ数が書かれている 2 枚のカードの組を選び、そのカードを場から取り除く。このようなカードの組が存在しない場合、操作を行えない。
先に操作を行えなくなった方が負けとなり、もう一方が勝ちとなります。 両者がそれぞれ勝つために最適な操作を選ぶ時、どちらが勝つか求めてください。
制約
- 1 \leq N \leq 18
- 1 \leq A_i,B_i \leq 10^9
- 入力は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
2 人とも最適に操作を行なったとき、高橋君が勝つ場合は Takahashi と、青木君が勝つ場合は Aoki と出力せよ。
入力例 1
5 1 9 2 5 4 9 1 4 2 5
出力例 1
Aoki
髙橋君が最初に取り除いた 2 枚が
-
1 枚目と 3 枚目のカードだった場合: 青木君は 2 枚目と 5 枚目のカードを取り除くことで勝つことができる。
-
1 枚目と 4 枚目のカードだった場合: 青木君は 2 枚目と 5 枚目のカードを取り除くことで勝つことができる。
-
2 枚目と 5 枚目のカードだった場合: 青木君は 1 枚目と 3 枚目のカードを取り除くことで勝つことができる。
髙橋君が最初の操作で取り除くことができるカードの組み合わせは以上の 3 通りのみで、髙橋君がどのような操作を行っても青木君が勝つことができるため、青木君が答えとなります。
入力例 2
9 3 2 1 7 4 1 1 8 5 2 9 8 2 1 6 8 5 2
出力例 2
Takahashi
Score : 475 points
Problem Statement
Takahashi and Aoki are playing a game using N cards. The front side of the i-th card has A_i written on it, and the back side has B_i written on it. Initially, the N cards are laid out on the table. With Takahashi going first, the two players take turns performing the following operation:
- Choose a pair of cards from the table such that either the numbers on their front sides are the same or the numbers on their back sides are the same, and remove these two cards from the table. If no such pair of cards exists, the player cannot perform the operation.
The player who is first to be unable to perform the operation loses, and the other player wins. Determine who wins if both players play optimally.
Constraints
- 1 \leq N \leq 18
- 1 \leq A_i, B_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Print Takahashi if Takahashi wins when both players play optimally, and Aoki otherwise.
Sample Input 1
5 1 9 2 5 4 9 1 4 2 5
Sample Output 1
Aoki
If Takahashi first removes
-
the first and third cards: Aoki can win by removing the second and fifth cards.
-
the first and fourth cards: Aoki can win by removing the second and fifth cards.
-
the second and fifth cards: Aoki can win by removing the first and third cards.
These are the only three pairs of cards Takahashi can remove in his first move, and Aoki can win in all cases. Therefore, the answer is Aoki.
Sample Input 2
9 3 2 1 7 4 1 1 8 5 2 9 8 2 1 6 8 5 2
Sample Output 2
Takahashi
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
1,\ldots,N の番号がついた N 個の街と、1,\ldots,M の番号がついた M 本の道路があります。
道路 i は街 A_i と B_i を結んでいます。道路を通行すると、所持している ポイント が次の通り増減します。
- 道路 i を使って、街 A_i から街 B_i に移動するときにはポイントが C_i 増加し、街 B_i から街 A_i に移動するときにはポイントが C_i 減少する。
所持しているポイントは負にもなりえます。
次の Q 個の質問に答えてください。
- 所持しているポイントが 0 である状態で街 X_i から移動を始めたとき、街 Y_i にいる状態で所持しているポイントの最大値を出力せよ。
ただし、街 X_i から街 Y_i に到達できないときはnan、街 Y_i にいる状態で所持しているポイントをいくらでも増やせるときはinfを代わりに出力せよ。
制約
- 2\leq N \leq 10^5
- 0\leq M \leq 10^5
- 1\leq Q \leq 10^5
- 1\leq A_i,B_i,X_i,Y_i \leq N
- 0\leq C_i \leq 10^9
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M Q A_1 B_1 C_1 \vdots A_M B_M C_M X_1 Y_1 \vdots X_Q Y_Q
出力
問題文の指示通りに Q 行出力せよ。
i 行目には i 番目の質問に対する答えを出力せよ。
入力例 1
5 5 3 1 2 1 1 2 2 3 4 1 4 5 1 3 5 2 5 3 1 2 3 1
出力例 1
-2 inf nan
1 番目の質問では、道路 5 を使って街 5 から街 3 に移動すると、ポイントを -2 所持している状態で街 3 にいることができます。
これ以上ポイントを大きくすることはできないので答えは -2 になります。
2 番目の質問では、「道路 2 を使って街 1 から街 2 に移動し、道路 1 を使って街 2 から街 1 に移動する」 という行動を好きなだけ繰り返したあと、道路 2 を使って街 1 から街 2 に移動することで、 街 2 にいる状態で所持しているポイントをいくらでも増やすことができます。
3 番目の質問では、街 3 から移動を始めて街 1 へ到達することはできません。
入力例 2
2 1 1 1 1 1 1 1
出力例 2
inf
始点と終点が同じ街である道路や、始点と終点が同じ街である質問が含まれることもあります。
入力例 3
9 7 5 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9
出力例 3
inf nan nan inf -9
Score : 500 points
Problem Statement
There are N towns numbered 1,\ldots,N and M roads numbered 1,\ldots,M.
Road i connects towns A_i and B_i. When you use a road, your score changes as follows:
- when you move from town A_i to town B_i using road i, your score increases by C_i; when you move from town B_i to town A_i using road i, your score decreases by C_i.
Your score may become negative.
Answer the following Q questions.
- If you start traveling from town X_i with initial score 0, find the maximum possible score when you are at town Y_i.
Here, if you cannot get from town X_i to town Y_i, printnaninstead; if you can have as large a score as you want when you are at town Y_i, printinfinstead.
Constraints
- 2\leq N \leq 10^5
- 0\leq M \leq 10^5
- 1\leq Q \leq 10^5
- 1\leq A_i,B_i,X_i,Y_i \leq N
- 0\leq C_i \leq 10^9
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N M Q A_1 B_1 C_1 \vdots A_M B_M C_M X_1 Y_1 \vdots X_Q Y_Q
Output
Print Q lines as specified in the Problem Statement.
The i-th line should contain the answer to the i-th question.
Sample Input 1
5 5 3 1 2 1 1 2 2 3 4 1 4 5 1 3 5 2 5 3 1 2 3 1
Sample Output 1
-2 inf nan
For the first question, if you use road 5 to move from town 5 to town 3, you can have a score -2 when you are at town 3.
Since you cannot make the score larger, the answer is -2.
For the second question, you can have as large a score as you want when you are at town 2 if you travel as follows: repeatedly "use road 2 to move from town 1 to town 2 and then use road 1 to move from town 2 to town 1" as many times as you want, and finally use road 2 to move from town 1 to town 2.
For the third question, you cannot get from town 3 to town 1.
Sample Input 2
2 1 1 1 1 1 1 1
Sample Output 2
inf
The endpoints of a road may be the same, and so may the endpoints given in a question.
Sample Input 3
9 7 5 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9
Sample Output 3
inf nan nan inf -9