A - Nine

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 100 点

問題文

以下のような、1 から 9 までの数字が書かれた 3 \times 3 の盤面があります。

1 以上 9 以下の整数 A,B が与えられます。ただし、A < B です。

A が書かれたマスと B が書かれたマスが左右に隣接しているか判定してください。

制約

  • 1 \le A < B \le 9
  • A, B は整数である。

入力

入力は以下の形式で標準入力から与えられる。

A B

出力

A が書かれたマスと B が書かれたマスが左右に隣接しているならば Yes、そうでないならば No を出力せよ。

入力例 1

7 8

出力例 1

Yes

7 が書かれたマスと 8 が書かれたマスは左右に隣り合っているので、Yes を出力します。

入力例 2

1 9

出力例 2

No

入力例 3

3 4

出力例 3

No

Score : 100 points

Problem Statement

We have the following 3 \times 3 board with integers from 1 through 9 written on it.

You are given two integers A and B between 1 and 9, where A < B.

Determine if the two squares with A and B written on them are adjacent horizontally.

Constraints

  • 1 \le A < B \le 9
  • A and B are integers.

Input

The input is given from Standard Input in the following format:

A B

Output

Print Yes if the two squares with A and B written on them are adjacent horizontally, and No otherwise.

Sample Input 1

7 8

Sample Output 1

Yes

The two squares with 7 and 8 written on them are adjacent horizontally, so print Yes.

Sample Input 2

1 9

Sample Output 2

No

Sample Input 3

3 4

Sample Output 3

No
B - Pawn on a Grid

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 100 点

問題文

上下左右に広がる H 行 W 列のマス目があり、各マスにはコマが置かれているか、何も置かれていないかのどちらかです。

マス目の状態は H 個の長さ W の文字列 S_1, S_2, \ldots, S_H によって表され、
S_i の j 文字目が # のとき上から i 行目かつ左から j 列目のマスにはコマが置かれていることを、
S_i の j 文字目が . のとき上から i 行目かつ左から j 列目のマスには何も置かれていないことを表しています。

マス目上のマスのうち、コマが置かれているようなものの個数を求めてください。

制約

  • 1\leq H,W \leq 10
  • H,W は整数
  • S_i は # と . のみからなる長さ W の文字列

入力

入力は以下の形式で標準入力から与えられる。

H W
S_1
S_2
\vdots
S_H

出力

コマが置かれているマスの個数を整数で出力せよ。

入力例 1

3 5
#....
.....
.##..

出力例 1

3
  • 上から 1 行目かつ左から 1 列目のマス
  • 上から 3 行目かつ左から 2 列目のマス
  • 上から 3 行目かつ左から 3 列目のマス

の計 3 つのマスにコマが置かれているため、3 を出力します。

入力例 2

1 10
..........

出力例 2

0

どのマスにもコマは置かれていないため、0 を出力します。

入力例 3

6 5
#.#.#
....#
..##.
####.
..#..
#####

出力例 3

16

Score : 100 points

Problem Statement

There is a grid with H rows from top to bottom and W columns from left to right. Each square has a piece placed on it or is empty.

The state of the grid is represented by H strings S_1, S_2, \ldots, S_H, each of length W.
If the j-th character of S_i is #, the square at the i-th row from the top and j-th column from the left has a piece on it;
if the j-th character of S_i is ., the square at the i-th row from the top and j-th column from the left is empty.

How many squares in the grid have pieces on them?

Constraints

  • 1\leq H,W \leq 10
  • H and W are integers.
  • S_i is a string of length W consisting of # and ..

Input

The input is given from Standard Input in the following format:

H W
S_1
S_2
\vdots
S_H

Output

Print the number of squares with pieces as an integer.

Sample Input 1

3 5
#....
.....
.##..

Sample Output 1

3

The following three squares have pieces on them:

  • the square at the 1-st row from the top and 1-st column from the left;
  • the square at the 3-rd row from the top and 2-nd column from the left;
  • the square at the 3-rd row from the top and 3-rd column from the left.

Thus, 3 should be printed.

Sample Input 2

1 10
..........

Sample Output 2

0

Since no square has a piece on it, 0 should be printed.

Sample Input 3

6 5
#.#.#
....#
..##.
####.
..#..
#####

Sample Output 3

16
C - Not All

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 200 点

問題文

長さ N の整数列 A=(A_1,A_2,\dots,A_N) および正整数 M が与えられます。

A の末尾の要素を削除するという操作を 0 回以上 N 回以下行うことで、以下の条件が満たされないようにしたいです。

  • 条件：A には 1 以上 M 以下の整数がすべて含まれている。

必要な操作回数の最小値を求めてください。

なお、本問題の制約下において、操作を 0 回以上 N 回以下行うことで上述の条件が満たされないようにすることが必ず可能であることが証明できます。

制約

  • 1\leq M \leq N \leq 100
  • 1\leq A_i \leq M
  • 入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 A_2 \dots A_N

出力

条件が満たされなくなるために必要な操作回数の最小値を出力せよ。

入力例 1

5 3
3 2 3 1 2

出力例 1

2

最初、A=(3,2,3,1,2) です。このとき、A には 1 以上 3 以下の整数がすべて含まれるため条件を満たします。

A の末尾の要素を削除する操作を 1 回行うと、A=(3,2,3,1) となります。このとき、A には 1 以上 3 以下の整数がすべて含まれるため条件を満たします。

A の末尾の要素を削除する操作をもう 1 回行うと、A=(3,2,3) となります。このとき、A には 1 が含まれないため条件を満たしません。

よって、条件が満たされなくなるために必要な操作回数の最小値は 2 です。

入力例 2

4 3
1 3 1 3

出力例 2

0

A には最初から 2 が含まれず条件を満たさないため、操作を 1 回も行う必要がありません。

入力例 3

10 4
1 3 3 4 2 1 3 1 2 4

出力例 3

6

Score : 200 points

Problem Statement

You are given an integer sequence A = (A_1, A_2, \dots, A_N) of length N and a positive integer M.

Your goal is to make the following condition false by performing this operation between 0 and N times (inclusive): remove the last element of A.

  • Condition: A contains every integer from 1 through M.

Find the minimum number of operations required.

Under the constraints of this problem, it can be proved that it is always possible to make the condition false by performing the operation between 0 and N times.

Constraints

  • 1 \le M \le N \le 100
  • 1 \le A_i \le M
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 A_2 \dots A_N

Output

Output the minimum number of operations required to make the condition false.

Sample Input 1

5 3
3 2 3 1 2

Sample Output 1

2

Initially, A = (3,2,3,1,2). Since A contains every integer from 1 through 3, the condition holds.

If you perform the operation once, A = (3,2,3,1). The condition still holds.

If you perform the operation once more, A = (3,2,3). The integer 1 is missing, so the condition no longer holds.

Therefore, the minimum required number of operations is 2.

Sample Input 2

4 3
1 3 1 3

Sample Output 2

0

Since A initially lacks the integer 2, the condition is already false, so no operation is needed.

Sample Input 3

10 4
1 3 3 4 2 1 3 1 2 4

Sample Output 3

6
D - Distance Table

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 200 点

問題文

N 個の駅、駅 1, 駅 2, \ldots, 駅 N が直線上にこの順に並んでいます。
ここで、1\leq i\leq N-1 について、駅 i と駅 (i+1) の間の距離は D_i です。

1\leq i<j\leq N をみたす整数の組 (i,j) それぞれについて、駅 i と駅 j の間の距離を求めてください。
なお、出力形式については出力の欄を参照してください。

制約

  • 2 \leq N \leq 50
  • 1 \leq D_i \leq 100
  • 入力はすべて整数

入力

入力は以下の形式で標準入力から与えられる。

N
D_1 D_2 \ldots D_{N-1}

出力

N-1 行出力せよ。
i 行目 (1\leq i\leq N-1) には、(N-i) 個の整数を空白区切りで出力せよ。
i 行目の j 番目 (1\leq j\leq N-i) には、駅 i と駅 (i+j) の間の距離を出力せよ。

入力例 1

5
5 10 2 3

出力例 1

5 15 17 20
10 12 15
2 5
3

各駅の間の距離は次のようになります。

  • 駅 1 と駅 2 の間の距離は 5 です。
  • 駅 1 と駅 3 の間の距離は 5+10=15 です。
  • 駅 1 と駅 4 の間の距離は 5+10+2=17 です。
  • 駅 1 と駅 5 の間の距離は 5+10+2+3=20 です。
  • 駅 2 と駅 3 の間の距離は 10 です。
  • 駅 2 と駅 4 の間の距離は 10+2=12 です。
  • 駅 2 と駅 5 の間の距離は 10+2+3=15 です。
  • 駅 3 と駅 4 の間の距離は 2 です。
  • 駅 3 と駅 5 の間の距離は 2+3=5 です。
  • 駅 4 と駅 5 の間の距離は 3 です。

よって、上記のように出力します。

入力例 2

2
100

出力例 2

100

Score : 200 points

Problem Statement

There are N stations, station 1, station 2, \ldots, station N, arranged in this order on a straight line.
Here, for 1\leq i\leq N-1, the distance between stations i and (i+1) is D_i.

For each pair of integers (i,j) satisfying 1\leq i<j\leq N, find the distance between stations i and j.
For the output format, refer to the Output section.

Constraints

  • 2 \leq N \leq 50
  • 1 \leq D_i \leq 100
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N
D_1 D_2 \ldots D_{N-1}

Output

Output N-1 lines.
On the i-th line (1\leq i\leq N-1), output (N-i) integers, separated by spaces.
The j-th integer on the i-th line (1\leq j\leq N-i) should be the distance between stations i and (i+j).

Sample Input 1

5
5 10 2 3

Sample Output 1

5 15 17 20
10 12 15
2 5
3

The distances between stations are as follows:

  • The distance between stations 1 and 2 is 5.
  • The distance between stations 1 and 3 is 5+10=15.
  • The distance between stations 1 and 4 is 5+10+2=17.
  • The distance between stations 1 and 5 is 5+10+2+3=20.
  • The distance between stations 2 and 3 is 10.
  • The distance between stations 2 and 4 is 10+2=12.
  • The distance between stations 2 and 5 is 10+2+3=15.
  • The distance between stations 3 and 4 is 2.
  • The distance between stations 3 and 5 is 2+3=5.
  • The distance between stations 4 and 5 is 3.

Thus, output as shown above.

Sample Input 2

2
100

Sample Output 2

100
E - Cycle Graph?

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 300 点

問題文

N 頂点 M 辺の単純無向グラフが与えられます。頂点には 1,2,\dots,N の番号が、辺には 1,2,\dots,M の番号がつけられており、辺 i は頂点 A_i と頂点 B_i を結んでいます。

このグラフがサイクルグラフであるか判定してください。

単純無向グラフとは 単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。

サイクルグラフとは 頂点に 1, 2, \dots, N の番号が付けられた N 頂点のグラフがサイクルグラフであるとは、(1, 2, \dots, N) を並べ変えて得られる数列 (v_1, v_2, \dots, v_N) であって、以下の条件を満たすものが存在することをいいます。
  • i = 1, 2, \dots, N-1 に対して、頂点 v_i と v_{i+1} を結ぶ辺が存在する
  • 頂点 v_N と v_1 を結ぶ辺が存在する
  • それら以外の辺は存在しない

制約

  • 3\leq N \leq 2\times 10^5
  • 0 \leq M \leq 2\times 10^5
  • 1 \leq A_i, B_i \leq N
  • 与えられるグラフは単純
  • 入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 B_1
\vdots
A_M B_M

出力

与えられたグラフがサイクルグラフであるなら Yes、そうでないなら No と出力せよ。

入力例 1

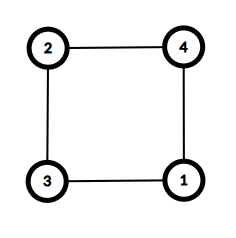
4 4
2 4
3 1
4 1
2 3

出力例 1

Yes

与えられたグラフは以下の通りであり、これはサイクルグラフです。

図

入力例 2

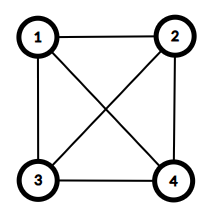
4 6
1 2
1 3
1 4
2 3
2 4
3 4

出力例 2

No

与えられたグラフは以下の通りであり、これはサイクルグラフではありません。

図

Score : 300 points

Problem Statement

You are given a simple undirected graph with N vertices and M edges. The vertices are numbered 1,2,\dots,N and the edges are numbered 1,2,\dots,M. Edge i connects vertices A_i and B_i.

Determine whether this graph is a cycle graph.

Definition of simple undirected graph A simple undirected graph is a graph with undirected edges without self-loops or multi-edges.

Definition of cycle graph An N-vertex graph with vertices labeled 1,2,\dots,N is a cycle graph when there exists a permutation (v_1,v_2,\dots,v_N) of (1,2,\dots,N) such that:
  • For each i = 1,2,\dots,N-1, there is an edge between vertices v_i and v_{i+1}.
  • There is an edge between vertices v_N and v_1.
  • No other edges exist.

Constraints

  • 3 \le N \le 2\times 10^5
  • 0 \le M \le 2\times 10^5
  • 1 \le A_i, B_i \le N
  • The given graph is simple.
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 B_1
\vdots
A_M B_M

Output

Output Yes if the given graph is a cycle graph; otherwise, print No.

Sample Input 1

4 4
2 4
3 1
4 1
2 3

Sample Output 1

Yes

The given graph is as follows, and this is a cycle graph.

Figure

Sample Input 2

4 6
1 2
1 3
1 4
2 3
2 4
3 4

Sample Output 2

No

The given graph is as follows, and this is not a cycle graph.

Figure