実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
A, B, C からなる長さ N の文字列 S が与えられます。
S の中で ABC が(連続な)部分文字列として初めて現れる位置を答えてください。すなわち、以下の条件を全て満たす整数 n のうち最小のものを答えてください。
- 1 \leq n \leq N - 2
- S の n 文字目から n+2 文字目までを取り出して出来る文字列は
ABCである。
ただし、ABC が S に現れない場合は -1 を出力してください。
制約
- 3 \leq N \leq 100
- S は
A,B,Cからなる長さ N の文字列
入力
入力は以下の形式で標準入力から与えられる。
N S
出力
S の中で ABC が部分文字列として初めて現れる位置を出力せよ。ただし、ABC が S に現れない場合は -1 を出力せよ。
入力例 1
8 ABABCABC
出力例 1
3
S の中で ABC が初めて現れるのは 3 文字目から 5 文字目までの位置です。よって 3 が答えになります。
入力例 2
3 ACB
出力例 2
-1
ABC が S に現れない場合は -1 を出力してください。
入力例 3
20 BBAAABBACAACABCBABAB
出力例 3
13
Score : 100 points
Problem Statement
You are given a string S of length N consisting of A, B, and C.
Find the position where ABC first appears as a (contiguous) substring in S. In other words, find the smallest integer n that satisfies all of the following conditions.
- 1 \leq n \leq N - 2.
- The string obtained by extracting the n-th through (n+2)-th characters of S is
ABC.
If ABC does not appear in S, print -1.
Constraints
- 3 \leq N \leq 100
- S is a string of length N consisting of
A,B, andC.
Input
The input is given from Standard Input in the following format:
N S
Output
Print the position where ABC first appears as a substring in S, or -1 if it does not appear in S.
Sample Input 1
8 ABABCABC
Sample Output 1
3
ABC first appears in S at the 3-rd through 5-th characters of S. Therefore, the answer is 3.
Sample Input 2
3 ACB
Sample Output 2
-1
If ABC does not appear in S, print -1.
Sample Input 3
20 BBAAABBACAACABCBABAB
Sample Output 3
13
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
0 以上 9999 以下の整数 N が与えられます。
N の先頭に必要なだけ 0 をつけ、4 桁の文字列にしたものを出力してください。
制約
- 0 \leq N \leq 9999
- N は整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを出力せよ。
入力例 1
321
出力例 1
0321
321 は 3 桁なので、先頭に 1 つ 0 をつけると 4 桁になります。
入力例 2
7777
出力例 2
7777
入力例 3
1
出力例 3
0001
Score : 100 points
Problem Statement
You are given an integer N between 0 and 9999 (inclusive).
Print it as a four-digit string after appending to it the necessary number of leading zeros.
Constraints
- 0 \leq N \leq 9999
- N is an integer.
Input
Input is given from Standard Input in the following format:
N
Output
Print the answer.
Sample Input 1
321
Sample Output 1
0321
321 has three digits, so we need to add one leading zero to it to make it have four digits.
Sample Input 2
7777
Sample Output 2
7777
Sample Input 3
1
Sample Output 3
0001
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
長さ N の正整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。
A が等比数列であるか判定してください。
制約
- 2\leq N\leq 100
- 1\leq A_i\leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
A が 等比数列ならば Yes を、そうでないならば No を出力せよ。
入力例 1
5 3 6 12 24 48
出力例 1
Yes
A=(3,6,12,24,48) です。
A は初項 3, 公比 2, 項数 5 の等比数列となっています。
よって、Yes を出力します。
入力例 2
3 1 2 3
出力例 2
No
A=(1,2,3) です。
A_1:A_2=1:2\neq 2:3=A_2:A_3 より、A は等比数列ではありません。
よって、No を出力します。
入力例 3
2 10 8
出力例 3
Yes
A は初項 10, 公比 0.8, 項数 2 の等比数列となっています。
よって、Yes を出力します。
Score : 200 points
Problem Statement
You are given a length-N sequence A=(A_1,A_2,\ldots,A_N) of positive integers.
Determine whether A is a geometric progression.
Constraints
- 2 \leq N \leq 100
- 1 \leq A_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
If A is a geometric progression, print Yes; otherwise, print No.
Sample Input 1
5 3 6 12 24 48
Sample Output 1
Yes
A=(3,6,12,24,48).
A is a geometric progression with first term 3, common ratio 2, and five terms.
Therefore, print Yes.
Sample Input 2
3 1 2 3
Sample Output 2
No
A=(1,2,3).
Since A_1 : A_2 = 1 : 2 \neq 2 : 3 = A_2 : A_3, A is not a geometric progression.
Therefore, print No.
Sample Input 3
2 10 8
Sample Output 3
Yes
A is a geometric progression with first term 10, common ratio 0.8, and two terms.
Therefore, print Yes.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
1 から N の番号がついた N 人の人がいます。
人 i はキーエンス本社ビルの建築面積を S_i 平方メートルであると予想しました。
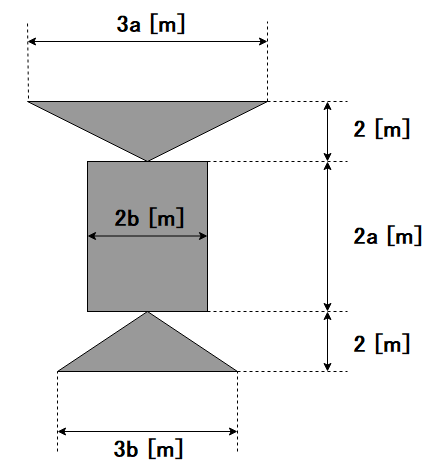
キーエンス本社ビルは下図のような形をしています。ただし、a,b はある 正の整数 です。
つまり、キーエンス本社ビルの建築面積は 4ab+3a+3b 平方メートルと表されます。
N 人のうち、この情報のみによって、予想した面積が確実に誤りであるとわかる人数を求めてください。
制約
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- 入力に含まれる値は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N S_1 \ldots S_N
出力
答えを出力せよ。
入力例 1
3 10 20 39
出力例 1
1
a=1,b=1 のとき面積は 10 平方メートル、a=2,b=3 のとき面積は 39 平方メートルとなります。
しかし a,b がどのような正の整数であったとしても面積が 20 平方メートルになることはありません。
よって、人 2 の予想だけは確実に誤りであることがわかります。
入力例 2
5 666 777 888 777 666
出力例 2
3
Score : 200 points
Problem Statement
There are N people numbered 1 to N.
Person i guessed the building area of KEYENCE headquarters building to be S_i square meters.
The shape of KEYENCE headquarters building is shown below, where a and b are some positive integers.
That is, the building area of the building can be represented as 4ab+3a+3b.
Based on just this information, how many of the N people are guaranteed to be wrong in their guesses?

Constraints
- 1 \leq N \leq 20
- 1 \leq S_i \leq 1000
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N S_1 \ldots S_N
Output
Print the answer.
Sample Input 1
3 10 20 39
Sample Output 1
1
The area would be 10 square meters if a=1,b=1, and 39 square meters if a=2,b=3.
However, no pair of positive integers a and b would make the area 20 square meters.
Thus, we can only be sure that Person 2 guessed wrong.
Sample Input 2
5 666 777 888 777 666
Sample Output 2
3
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
英小文字のみからなる N 個の文字列 S_1,S_2,\dots,S_N が与えられます。
S_1,S_2,\dots,S_N から文字列を好きな個数選ぶことを考えます。
このとき、「選んだ文字列の中でちょうど K 個の文字列に登場する英小文字」の種類数としてあり得る最大値を求めてください。
制約
- 1 \le N \le 15
- 1 \le K \le N
- N,K は整数
- S_i は英小文字からなる空でない文字列である。
- 1 \le i \le N を満たす整数 i に対し、S_i に同じ文字は 2 個以上含まれない。
- i \neq j ならば S_i \neq S_j である。
入力
入力は以下の形式で標準入力から与えられる。
N K S_1 S_2 \vdots S_N
出力
答えを出力せよ。
入力例 1
4 2 abi aef bc acg
出力例 1
3
S_1,S_3,S_4 を選んだ場合、a,b,c がちょうど 2 個の文字列に含まれます。
4 個以上の文字がちょうど 2 個の文字列に含まれるような選び方は存在しないため、答えは 3 です。
入力例 2
2 2 a b
出力例 2
0
同じ文字列を複数回選ぶことはできません。
入力例 3
5 2 abpqxyz az pq bc cy
出力例 3
7
Score : 300 points
Problem Statement
You are given N strings S_1,S_2,\dots,S_N consisting of lowercase English alphabets.
Consider choosing some number of strings from S_1,S_2,\dots,S_N.
Find the maximum number of distinct alphabets that satisfy the following condition: "the alphabet is contained in exactly K of the chosen strings."
Constraints
- 1 \le N \le 15
- 1 \le K \le N
- N and K are integers.
- S_i is a non-empty string consisting of lowercase English alphabets.
- For each integer i such that 1 \le i \le N, S_i does not contain two or more same alphabets.
- If i \neq j, then S_i \neq S_j.
Input
Input is given from Standard Input in the following format:
N K S_1 S_2 \vdots S_N
Output
Print the answer.
Sample Input 1
4 2 abi aef bc acg
Sample Output 1
3
When S_1,S_3, and S_4 are chosen, a,b, and c occur in exactly two of the strings.
There is no way to choose strings so that 4 or more alphabets occur in exactly 2 of the strings, so the answer is 3.
Sample Input 2
2 2 a b
Sample Output 2
0
You cannot choose the same string more than once.
Sample Input 3
5 2 abpqxyz az pq bc cy
Sample Output 3
7
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
縦 H マス横 W マスのグリッドがあります。グリッドの上から i 行目、左から j 列目のマスを (i, j) と呼びます。
グリッドの各マスには # と . のいずれかの文字が書かれています。(i, j) に書かれている文字を C[i][j] とします。また、整数 i, j が 1 \leq i \leq H と 1 \leq j \leq W の少なくとも一方を満たさない場合、 C[i][j] を . と定義します。
正整数 a, b, n が以下の条件を全て満たす時、(a,b) および (a+d,b+d),(a+d,b-d),(a-d,b+d),(a-d,b-d) (1 \leq d \leq n) の 4n + 1 マスを (a,b) を中心とするサイズ n のバツ印 と呼びます。
- C[a][b] は
#である。 - 1 \leq d \leq n を満たす整数 d について、 C[a+d][b+d],C[a+d][b-d],C[a-d][b+d],C[a-d][b-d] はいずれも
#である。 - C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1],C[a-n-1][b-n-1] のうち少なくとも 1 つは
.である。
例えば次の図で示された例では、(2, 2) を中心とするサイズ 1 のバツ印と (3, 7) を中心とするサイズ 2 のバツ印がグリッド上にあります。

グリッドにはいくつかのバツ印があります。バツ印を構成するマス以外に # は書かれていません。
また、異なるバツ印を構成するマス同士は頂点を共有しません。以下の 2 つのグリッドは異なるバツ印を構成するマス同士が頂点を共有している例で、このようなグリッドの状態は入力として与えられません。 例えば左のグリッドでは (3, 3) と (4, 4) が頂点を共有しているのが条件に反しています。

N = \min(H, W) とします。また、サイズ n のバツ印の個数を S_n とします。S_1, S_2, \dots, S_N を計算してください。
制約
- 3 \leq H, W \leq 100
- C[i][j] は
#または. - 異なるバツ印を構成するマス同士は頂点を共有しない
- H, W は整数
入力
入力は以下の形式で標準入力から与えられる。
H W C[1][1]C[1][2]\dots C[1][W] C[2][1]C[2][2]\dots C[2][W] \vdots C[H][1]C[H][2]\dots C[H][W]
出力
S_1, S_2, \dots, S_N を空白区切りで出力せよ。
入力例 1
5 9 #.#.#...# .#...#.#. #.#...#.. .....#.#. ....#...#
出力例 1
1 1 0 0 0
問題文に書かれた説明の通り、(2, 2) を中心とするサイズ 1 のバツ印と (3, 7) を中心とするサイズ 2 のバツ印が書かれています。
入力例 2
3 3 ... ... ...
出力例 2
0 0 0
バツ印が 1 個も書かれていない場合もあります。
入力例 3
3 16 #.#.....#.#..#.# .#.......#....#. #.#.....#.#..#.#
出力例 3
3 0 0
入力例 4
15 20 #.#..#.............# .#....#....#.#....#. #.#....#....#....#.. ........#..#.#..#... #.....#..#.....#.... .#...#....#...#..#.# ..#.#......#.#....#. ...#........#....#.# ..#.#......#.#...... .#...#....#...#..... #.....#..#.....#.... ........#.......#... #.#....#....#.#..#.. .#....#......#....#. #.#..#......#.#....#
出力例 4
5 0 1 0 0 0 1 0 0 0 0 0 0 0 0
Score : 300 points
Problem Statement
We have a grid with H horizontal rows and W vertical columns. We denote by (i, j) the cell at the i-th row from the top and j-th column from the left of the grid.
Each cell in the grid has a symbol # or . written on it. Let C[i][j] be the character written on (i, j). For integers i and j such that at least one of 1 \leq i \leq H and 1 \leq j \leq W is violated, we define C[i][j] to be ..
(4n+1) squares, consisting of (a, b) and (a+d,b+d),(a+d,b-d),(a-d,b+d),(a-d,b-d) (1 \leq d \leq n, 1 \leq n), are said to be a cross of size n centered at (a,b) if and only if all of the following conditions are satisfied:
- C[a][b] is
#. - C[a+d][b+d],C[a+d][b-d],C[a-d][b+d], and C[a-d][b-d] are all
#, for all integers d such that 1 \leq d \leq n, - At least one of C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1], and C[a-n-1][b-n-1] is
..
For example, the grid in the following figure has a cross of size 1 centered at (2, 2) and another of size 2 centered at (3, 7).

The grid has some crosses. No # is written on the cells except for those comprising a cross.
Additionally, no two squares that comprise two different crosses share a corner. The two grids in the following figure are the examples of grids where two squares that comprise different crosses share a corner; such grids are not given as an input. For example, the left grid is invalid because (3, 3) and (4, 4) share a corner.

Let N = \min(H, W), and S_n be the number of crosses of size n. Find S_1, S_2, \dots, S_N.
Constraints
- 3 \leq H, W \leq 100
- C[i][j] is
#or.. - No two different squares that comprise two different crosses share a corner.
- H and W are integers.
Input
The input is given from Standard Input in the following format:
H W C[1][1]C[1][2]\dots C[1][W] C[2][1]C[2][2]\dots C[2][W] \vdots C[H][1]C[H][2]\dots C[H][W]
Output
Print S_1, S_2, \dots, and S_N, separated by spaces.
Sample Input 1
5 9 #.#.#...# .#...#.#. #.#...#.. .....#.#. ....#...#
Sample Output 1
1 1 0 0 0
As described in the Problem Statement, there are a cross of size 1 centered at (2, 2) and another of size 2 centered at (3, 7).
Sample Input 2
3 3 ... ... ...
Sample Output 2
0 0 0
There may be no cross.
Sample Input 3
3 16 #.#.....#.#..#.# .#.......#....#. #.#.....#.#..#.#
Sample Output 3
3 0 0
Sample Input 4
15 20 #.#..#.............# .#....#....#.#....#. #.#....#....#....#.. ........#..#.#..#... #.....#..#.....#.... .#...#....#...#..#.# ..#.#......#.#....#. ...#........#....#.# ..#.#......#.#...... .#...#....#...#..... #.....#..#.....#.... ........#.......#... #.#....#....#.#..#.. .#....#......#....#. #.#..#......#.#....#
Sample Output 4
5 0 1 0 0 0 1 0 0 0 0 0 0 0 0
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
整数 N が与えられるので、以下の条件を全て満たす最小の整数 X を求めてください。
- X は N 以上である。
- 非負整数 (a,b) の組であって、 X=a^3+a^2b+ab^2+b^3 を満たすようなものが存在する。
制約
- N は整数
- 0 \le N \le 10^{18}
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを整数として出力せよ。
入力例 1
9
出力例 1
15
9 \le X \le 14 であるようなどの整数 X についても、問題文中の条件を満たすような (a,b) は存在しません。
X=15 は (a,b)=(2,1) とすると問題文中の条件を満たします。
入力例 2
0
出力例 2
0
N 自身が条件を満たすこともあります。
入力例 3
999999999989449206
出力例 3
1000000000000000000
入出力が 32bit 整数型に収まらない場合があります。
Score : 400 points
Problem Statement
Given an integer N, find the smallest integer X that satisfies all of the conditions below.
- X is greater than or equal to N.
- There is a pair of non-negative integers (a, b) such that X=a^3+a^2b+ab^2+b^3.
Constraints
- N is an integer.
- 0 \le N \le 10^{18}
Input
Input is given from Standard Input in the following format:
N
Output
Print the answer as an integer.
Sample Input 1
9
Sample Output 1
15
For any integer X such that 9 \le X \le 14, there is no (a, b) that satisfies the condition in the statement.
For X=15, (a,b)=(2,1) satisfies the condition.
Sample Input 2
0
Sample Output 2
0
N itself may satisfy the condition.
Sample Input 3
999999999989449206
Sample Output 3
1000000000000000000
Input and output may not fit into a 32-bit integer type.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
長さ N の数列 A=(A_1,A_2,\ldots,A_N) が与えられます。ここで、各 A_i (1\leq i\leq N) は 1\leq A_i \leq N をみたします。
高橋君と青木君が N 回ゲームを行います。i=1,2,\ldots,N 回目のゲームは次のようにして行われます。
- 青木君が正整数 K_i を指定する。
- 青木君の指定した K_i を聞いた後、高橋君は 1 以上 N 以下の整数 S_i を選び、黒板に書く。
-
その後、 K_i 回次の操作を繰り返す。
- 黒板に x が書かれているとき、それを消し、A_x を新しく書く。
K_i 回の操作の後で黒板に書かれている整数が i ならば i 回目のゲームは高橋君の勝ち、そうでないならば青木君の勝ちとなります。
ここで、K_i,S_i は i=1,2,\ldots,N に対して独立に選ぶ事ができます。
両者が、自身が勝つために最善の行動をとったとき、N 回のゲームのうち高橋君が勝つ回数を求めてください。
制約
- 1\leq N\leq 2\times 10^5
- 1\leq A_i\leq N
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
両者が最善の行動をとったとき、N 回のゲームのうち高橋君が勝つ回数を出力せよ。
入力例 1
3 2 2 3
出力例 1
2
1 回目のゲームにおいて、青木君が K_1=2 を指定したとき、高橋君は S_1 として、1,2,3 のいずれを選んでも勝つことはできません。
例えば、高橋君が最初に黒板に S_1=1 と書いたとすると、2 回の操作で黒板に書かれている数は順に 1\to 2(=A_1) 、2\to 2(=A_2) と変化し、
最終的に黒板に書かれている数は 2(\neq 1) であるため、青木君の勝ちとなります。
一方、2,3 回目のゲームにおいては、青木君の指定した K_i の値によらず、高橋君はそれぞれ 2,3 を最初に黒板に書くことで勝つ事ができます。
よって、両者が、自分が勝つために最善の行動をとったとき、高橋君が勝つゲームは 2,3 回目の 2 回であるため、2 を出力します。
入力例 2
2 2 1
出力例 2
2
1 回目のゲームにおいて、高橋君は、青木君が指定した K_1 が奇数のときは 2、偶数のときは 1 を最初に黒板に書く事で勝つ事ができます。
同様に 2 回目のゲームにおいても勝つ方法が存在するため、1,2 回目のゲームのいずれでも高橋君は勝利する事ができ、2 が答えとなります。
Score : 500 points
Problem Statement
You are given a sequence of N numbers: A=(A_1,A_2,\ldots,A_N). Here, each A_i (1\leq i\leq N) satisfies 1\leq A_i \leq N.
Takahashi and Aoki will play N rounds of a game. For each i=1,2,\ldots,N, the i-th game will be played as follows.
- Aoki specifies a positive integer K_i.
- After knowing K_i Aoki has specified, Takahashi chooses an integer S_i between 1 and N, inclusive, and writes it on a blackboard.
-
Repeat the following K_i times.
- Replace the integer x written on the blackboard with A_x.
If i is written on the blackboard after the K_i iterations, Takahashi wins the i-th round; otherwise, Aoki wins.
Here, K_i and S_i can be chosen independently for each i=1,2,\ldots,N.
Find the number of rounds Takahashi wins if both players play optimally to win.
Constraints
- 1\leq N\leq 2\times 10^5
- 1\leq A_i\leq N
- All values in the input are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Find the number of rounds Takahashi wins if both players play optimally to win.
Sample Input 1
3 2 2 3
Sample Output 1
2
In the first round, if Aoki specifies K_1=2, Takahashi cannot win whichever option he chooses for S_1: 1, 2, or 3.
For example, if Takahashi writes S_1=1 on the initial blackboard, the two operations will change this number as follows: 1\to 2(=A_1), 2\to 2(=A_2). The final number on the blackboard will be 2(\neq 1), so Aoki wins.
On the other hand, in the second and third rounds, Takahashi can win by writing 2 and 3, respectively, on the initial blackboard, whatever value Aoki specifies as K_i.
Therefore, if both players play optimally to win, Takashi wins two rounds: the second and the third. Thus, you should print 2.
Sample Input 2
2 2 1
Sample Output 2
2
In the first round, Takahashi can win by writing 2 on the initial blackboard if K_1 specified by Aoki is odd, and 1 if it is even.
Similarly, there is a way for Takahashi to win the second round. Thus, Takahashi can win both rounds: the answer is 2.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
N + Q 頂点のグラフがあり、頂点には 1, 2, \ldots, N + Q の番号がついています。グラフにははじめ辺がありません。
このグラフに対して i = 1, 2, \ldots, Q の順に以下の操作を行います。
- L_i \leq j \leq R_i を満たす各整数 j について頂点 N + i と頂点 j の間にコスト C_i の無向辺を追加する
すべての操作を終えた後グラフは連結であるか判定し、連結である場合はこのグラフの最小全域木のコストを求めてください。
ただし、最小全域木とはコストが最小の全域木のことを指し、全域木のコストとは全域木に使われた辺のコストの和のことを指します。
制約
- 1 \leq N, Q \leq 2 \times 10^5
- 1 \leq L_i \leq R_i \leq N
- 1 \leq C_i \leq 10^9
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N Q L_1 R_1 C_1 L_2 R_2 C_2 \vdots L_Q R_Q C_Q
出力
グラフが連結である場合は最小全域木のコストを出力せよ。そうでない場合は -1 を出力せよ。
入力例 1
4 3 1 2 2 1 3 4 2 4 5
出力例 1
22
以下の辺からなる全域木が最小全域木のひとつとなります。
- 頂点 1 と 5 を結ぶコスト 2 の辺
- 頂点 2 と 5 を結ぶコスト 2 の辺
- 頂点 1 と 6 を結ぶコスト 4 の辺
- 頂点 3 と 6 を結ぶコスト 4 の辺
- 頂点 3 と 7 を結ぶコスト 5 の辺
- 頂点 4 と 7 を結ぶコスト 5 の辺
2 + 2 + 4 + 4 + 5 + 5 = 22 であるため、22 を出力します。
入力例 2
6 2 1 2 10 4 6 10
出力例 2
-1
グラフは非連結です。
入力例 3
200000 4 1 200000 1000000000 1 200000 998244353 1 200000 999999999 1 200000 999999999
出力例 3
199651870599998
Score : 500 points
Problem Statement
There is a graph with N + Q vertices, numbered 1, 2, \ldots, N + Q. Initially, the graph has no edges.
For this graph, perform the following operation for i = 1, 2, \ldots, Q in order:
- For each integer j satisfying L_i \leq j \leq R_i, add an undirected edge with cost C_i between vertices N + i and j.
Determine if the graph is connected after all operations are completed. If it is connected, find the cost of a minimum spanning tree of the graph.
A minimum spanning tree is a spanning tree with the smallest possible cost, and the cost of a spanning tree is the sum of the costs of the edges used in the spanning tree.
Constraints
- 1 \leq N, Q \leq 2 \times 10^5
- 1 \leq L_i \leq R_i \leq N
- 1 \leq C_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q L_1 R_1 C_1 L_2 R_2 C_2 \vdots L_Q R_Q C_Q
Output
If the graph is connected, print the cost of a minimum spanning tree. Otherwise, print -1.
Sample Input 1
4 3 1 2 2 1 3 4 2 4 5
Sample Output 1
22
The following edges form a minimum spanning tree:
- An edge with cost 2 connecting vertices 1 and 5
- An edge with cost 2 connecting vertices 2 and 5
- An edge with cost 4 connecting vertices 1 and 6
- An edge with cost 4 connecting vertices 3 and 6
- An edge with cost 5 connecting vertices 3 and 7
- An edge with cost 5 connecting vertices 4 and 7
Since 2 + 2 + 4 + 4 + 5 + 5 = 22, print 22.
Sample Input 2
6 2 1 2 10 4 6 10
Sample Output 2
-1
The graph is disconnected.
Sample Input 3
200000 4 1 200000 1000000000 1 200000 998244353 1 200000 999999999 1 200000 999999999
Sample Output 3
199651870599998