Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
整数 W,B が与えられるので、以下の問題を解いてください。
高橋君の体重は W {\rm [kg]} です。 (単位が {\rm kg} であることに注意してください)
風船を n 個付けられた物体は、物体の質量が nB {\rm [g]} 未満 である時、またその時に限り、空に飛び立ちます。
高橋君を空に飛ばすためには、最低何個の風船を付ける必要がありますか?
制約
- 1 \le W \le 100
- 1 \le B \le 100
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
W B
出力
答えを出力せよ。
入力例 1
80 5
出力例 1
16001
高橋君の体重は 80 {\rm kg} = 80000 {\rm g} です。
高橋君に風船を 16001 個付けると、高橋君の質量は 16001 \times 5=80005 {\rm g} 未満であるため、空に飛び立ちます。
16000 個では不十分であることに注意してください。
入力例 2
70 6
出力例 2
11667
入力例 3
100 100
出力例 3
1001
Score : 100 points
Problem Statement
Given integers W and B, solve the following problem.
Takahashi's weight is W {\rm [kg]}. (Note that the unit is {\rm kg}.)
An object attached with n balloons will fly into the sky if and only if the mass of the object is strictly less than nB {\rm [g]}.
What is the minimum number of balloons needed to make Takahashi fly into the sky?
Constraints
- 1 \le W \le 100
- 1 \le B \le 100
- All input values are integers.
Input
The input is given from Standard Input in the following format:
W B
Output
Output the answer.
Sample Input 1
80 5
Sample Output 1
16001
Takahashi's weight is 80 {\rm kg} = 80000 {\rm g}.
If he is attached with 16001 balloons, his mass is less than 16001 \times 5=80005 {\rm g}, so he will fly into the sky.
Note that 16000 balloons are not sufficient.
Sample Input 2
70 6
Sample Output 2
11667
Sample Input 3
100 100
Sample Output 3
1001
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
空に M 種類の鳥が合わせて N 羽飛んでいます。
鳥の種類には 1,2,\dots,M の番号が付けられています。
N 羽の鳥には 1,2,\dots,N の番号が付けられており、鳥 i の種類は A_i で、大きさは B_i です。
全ての k=1,2,\dots,M について、飛んでいる種類 k の鳥の大きさの平均値を求めてください。
ただし、全ての k=1,2,\dots,M について、種類 k の鳥が 1 羽以上飛んでいることが保証されます。
制約
- 1 \le M \le N \le 100
- 1 \le A_i \le M
- 1 \le B_i \le 100
- 種類 k の鳥が少なくとも 1 羽存在する ( 1 \le k \le M )
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
M 行出力せよ。
k ( 1 \le k \le M ) 行目には、種類 k の鳥の大きさの平均値を出力せよ。
真の解との絶対誤差または相対誤差が 10^{-5} 以下であるとき、正解とみなされる。
入力例 1
10 5 4 92 1 16 3 77 4 99 2 89 3 8 1 40 5 56 1 40 4 77
出力例 1
32.00000000000000000000 89.00000000000000000000 42.50000000000000000000 89.33333333333333333333 56.00000000000000000000
- 種類 1 の鳥の大きさの平均値は (16+40+40)/3 = 32 です。
- 種類 2 の鳥の大きさの平均値は 89 です。
- 種類 3 の鳥の大きさの平均値は (77+8)/2 = 42.5 です。
- 種類 4 の鳥の大きさの平均値は (92+99+77)/3 \approx 89.3333 です。
- 種類 5 の鳥の大きさの平均値は 56 です。
Score : 200 points
Problem Statement
There are N birds of M types flying in the sky.
The bird types are numbered 1,2,\dots,M.
The N birds are numbered 1,2,\dots,N, and bird i is of type A_i and has size B_i.
For every k=1,2,\dots,M, find the average size of the flying birds of type k.
It is guaranteed that for every k=1,2,\dots,M, there is at least one bird of type k flying.
Constraints
- 1 \le M \le N \le 100
- 1 \le A_i \le M
- 1 \le B_i \le 100
- There exists at least one bird of type k ( 1 \le k \le M ).
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Output M lines.
The k-th line ( 1 \le k \le M ) should contain the average size of birds of type k.
Your answer will be considered correct if the absolute or relative error from the true value is at most 10^{-5}.
Sample Input 1
10 5 4 92 1 16 3 77 4 99 2 89 3 8 1 40 5 56 1 40 4 77
Sample Output 1
32.00000000000000000000 89.00000000000000000000 42.50000000000000000000 89.33333333333333333333 56.00000000000000000000
- The average size of birds of type 1 is (16+40+40)/3 = 32.
- The average size of birds of type 2 is 89.
- The average size of birds of type 3 is (77+8)/2 = 42.5.
- The average size of birds of type 4 is (92+99+77)/3 \approx 89.3333.
- The average size of birds of type 5 is 56.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
高橋君は風船で空を飛ぶことにしました。高橋君は時刻 0 (単位は秒) の時点で高度 H にいて、これから 10^9 秒間飛行します。
高橋君は自身が飛んでいる高度を 1 秒あたり 1 まで変化させることが出来ます。ただし、高度を 0 以下にすることはできません。
- 言い換えると、高橋君の時刻 t における高度を F(t) とした時、F(t) は以下の条件を全て満たします。
- F(0) = H
- 0 \leq t \lt u \leq 10^9 において -1 \leq \dfrac{F(u) - F(t)}{u - t} \leq 1
- 0 \leq t \leq 10^9 において F(t) \gt 0
N 個の高度に関する目標があります。i 個目の目標は時刻 t_i 時点での高度を l_i 以上 u_i 以下にすることです。
高橋君は目標を全て達成するような飛行が可能ですか?
T 個のテストケースが与えられるので、それぞれに対して答えを求めてください。
制約
- 1 \leq T \leq 10^5
- 1 \leq N \leq 10^5
- 1 \leq H \leq 10^9
- 1 \leq t_1 \lt t_2 \lt \dots \lt t_N \leq 10^9
- 1 \leq l_i \leq u_i \leq 10^9
- 全てのテストケースにおける N の総和は 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。ここで \mathrm{case}_i は i 番目のテストケースを意味する。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
各テストケースは以下の形式で与えられる。
N H t_1 l_1 u_1 t_2 l_2 u_2 \vdots t_N l_N u_N
出力
T 行出力せよ。i 行目には、i 番目のテストケースにおいて目標を全て達成するような飛行が可能である場合 Yes を、そうでない場合 No を出力せよ。
入力例 1
3 2 5 3 1 4 8 9 11 2 6 1 1 4 3 5 8 10 36 27 37 38 30 34 54 38 20 77 45 1 36 49 38 51 52 31 58 65 43 60 71 14 42 73 36 38 85 14 29
出力例 1
Yes No Yes
1 番目のテストケースについて、高橋君は以下の方法で飛行することで全ての目標を達成することが出来ます。
- 時刻 0 の時点で高橋君は高度 5 にいる。
- 時刻 0 から時刻 2 にかけて高橋君は秒速 0.5 で高度を下げる。
- 時刻 2 の時点で高橋君は高度 5 - 0.5 \times 2 = 4 にいる。
- 時刻 2 から時刻 3 の間、高橋君は同じ高度にとどまる。
- 時刻 3 の時点で高橋君は高度 4 にいる。高橋君は 1 番目の目標を満たす。
- 時刻 3 から時刻 8 にかけて高橋君は秒速 1 で高度を上げる。
- 時刻 8 の時点で高橋君は高度 4 + 1 \times 5 = 9 にいる。高橋君は 2 番目の目標を満たす。
2 番目のテストケースについて、高橋君はどのように飛行しても目標を全て達成することは出来ません。
Score : 300 points
Problem Statement
Takahashi has decided to fly in the sky with balloons. Takahashi is at altitude H at time 0 (the unit is seconds), and will fly for 10^9 seconds from now.
Takahashi can change his flying altitude by up to 1 per second. However, he cannot make his altitude 0 or less.
- In other words, if F(t) denotes Takahashi's altitude at time t, then F(t) satisfies all of the following conditions:
- F(0) = H
- -1 \leq \dfrac{F(u) - F(t)}{u - t} \leq 1 for 0 \leq t \lt u \leq 10^9.
- F(t) \gt 0 for 0 \leq t \leq 10^9.
There are N goals regarding altitude. The i-th goal is to make the altitude at time t_i at least l_i and at most u_i.
Is it possible for Takahashi to fly in a way that achieves all goals?
You are given T test cases; solve each of them.
Constraints
- 1 \leq T \leq 10^5
- 1 \leq N \leq 10^5
- 1 \leq H \leq 10^9
- 1 \leq t_1 \lt t_2 \lt \dots \lt t_N \leq 10^9
- 1 \leq l_i \leq u_i \leq 10^9
- The sum of N over all test cases is at most 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format, where \mathrm{case}_i denotes the i-th test case.
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
Each test case is given in the following format:
N H t_1 l_1 u_1 t_2 l_2 u_2 \vdots t_N l_N u_N
Output
Output T lines. The i-th line should contain Yes if it is possible to fly in a way that achieves all goals in the i-th test case, and No otherwise.
Sample Input 1
3 2 5 3 1 4 8 9 11 2 6 1 1 4 3 5 8 10 36 27 37 38 30 34 54 38 20 77 45 1 36 49 38 51 52 31 58 65 43 60 71 14 42 73 36 38 85 14 29
Sample Output 1
Yes No Yes
For the first test case, Takahashi can achieve all goals by flying as follows:
- At time 0, he is at altitude 5.
- From time 0 to time 2, he descends at a rate of 0.5 per second.
- At time 2, he is at altitude 5 - 0.5 \times 2 = 4.
- From time 2 to time 3, he stays at the same altitude.
- At time 3, he is at altitude 4. He satisfies the first goal.
- From time 3 to time 8, he ascends at a rate of 1 per second.
- At time 8, he is at altitude 4 + 1 \times 5 = 9. He satisfies the second goal.
For the second test case, he cannot achieve all goals no matter how he flies.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
空は 2000 \times 2000 のマス目で表されます。
空を見上げた時、上から r 行目、左から c 列目にあるマスを (r,c) と呼びます。
いま、この空には雲 1,2,\dots,N が浮かんでいます。
整数の組 (r,c) が U_i \le r \le D_i, L_i \le c \le R_i を満たすとき、またその時に限り、 (r,c) は雲 i で覆われています。
k=1,2,\dots,N について、以下の問いに答えてください。
- N 個の雲のうち、雲 k のみを取り除く。この時点で空には N-1 個の雲が浮かんでいる。このとき、どの雲にも覆われていないマスがいくつあるか答えよ。
制約
- 1 \le N \le 2 \times 10^5
- 1 \le U_i \le D_i \le 2000
- 1 \le L_i \le R_i \le 2000
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N U_1 D_1 L_1 R_1 U_2 D_2 L_2 R_2 \vdots U_N D_N L_N R_N
出力
N 行出力せよ。
i 行目には、 k=i とした場合の問いの答えを出力せよ。
入力例 1
5 2 4 1 4 3 3 3 5 1 3 4 6 4 5 3 5 5 5 4 6
出力例 1
3999983 3999976 3999982 3999978 3999977
図は、空のうち左上 5 \times 6 の領域を抜き出したものです。
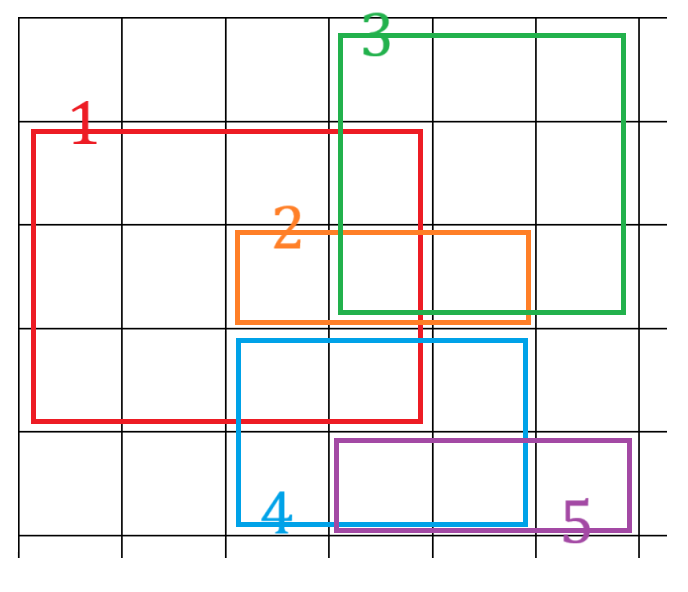
- 雲 1 を取り除いた際、何らかの雲に覆われているマスは 17 マスなので、どの雲にも覆われていないマスは 3999983 マスです。
- 雲 2 を取り除いた際、何らかの雲に覆われているマスは 24 マスなので、どの雲にも覆われていないマスは 3999976 マスです。
- 雲 3 を取り除いた際、何らかの雲に覆われているマスは 18 マスなので、どの雲にも覆われていないマスは 3999982 マスです。
- 雲 4 を取り除いた際、何らかの雲に覆われているマスは 22 マスなので、どの雲にも覆われていないマスは 3999978 マスです。
- 雲 5 を取り除いた際、何らかの雲に覆われているマスは 23 マスなので、どの雲にも覆われていないマスは 3999977 マスです。
Score : 425 points
Problem Statement
The sky is represented by a 2000 \times 2000 grid.
When looking up at the sky, the cell at the r-th row from the top and c-th column from the left is called (r,c).
Currently, there are clouds 1,2,\dots,N floating in this sky.
The cell (r,c) is covered by cloud i if and only if it satisfies U_i \le r \le D_i and L_i \le c \le R_i.
For k=1,2,\dots,N, answer the following question:
- Remove only cloud k from the N clouds. At this point, there are N-1 clouds floating in the sky. How many cells are not covered by any cloud?
Constraints
- 1 \le N \le 2 \times 10^5
- 1 \le U_i \le D_i \le 2000
- 1 \le L_i \le R_i \le 2000
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N U_1 D_1 L_1 R_1 U_2 D_2 L_2 R_2 \vdots U_N D_N L_N R_N
Output
Output N lines.
The i-th line should contain the answer to the question when k=i.
Sample Input 1
5 2 4 1 4 3 3 3 5 1 3 4 6 4 5 3 5 5 5 4 6
Sample Output 1
3999983 3999976 3999982 3999978 3999977
The figure shows the top-left 5 \times 6 region of the sky.

- When cloud 1 is removed, the number of cells covered by some cloud is 17, so the number of cells not covered by any cloud is 3999983.
- When cloud 2 is removed, the number of cells covered by some cloud is 24, so the number of cells not covered by any cloud is 3999976.
- When cloud 3 is removed, the number of cells covered by some cloud is 18, so the number of cells not covered by any cloud is 3999982.
- When cloud 4 is removed, the number of cells covered by some cloud is 22, so the number of cells not covered by any cloud is 3999978.
- When cloud 5 is removed, the number of cells covered by some cloud is 23, so the number of cells not covered by any cloud is 3999977.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
1 から N の番号がついた N 匹のウサギが数直線上にいます。ウサギ i は座標 X_i にいます。同じ座標に複数のウサギがいることもあります。
ウサギは ジャンプ力 というパラメータを持っていて、ウサギ i のジャンプ力は R_i です。
これから全てのウサギがちょうど 1 回ずつジャンプします。座標 x にいるジャンプ力 r のウサギがジャンプすると座標 x+r または座標 x-r に移動します。
それぞれのウサギがどちらの座標にジャンプするかを自由に選べる時、全てのウサギがジャンプした後にウサギがいる座標の種類数としてあり得る最大値を求めてください。
制約
- 1 \leq N \leq 2 \times 10^5
- -10^9 \leq X_i \leq 10^9
- 1 \leq R_i \leq 10^9
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N X_1 R_1 X_2 R_2 \vdots X_N R_N
出力
ジャンプ後にウサギがいる座標の種類数としてあり得る最大値を出力せよ。
入力例 1
3 4 1 2 3 4 5
出力例 1
3
以下に示すようにそれぞれのウサギが移動すると、ジャンプ後にウサギがいる座標の種類数として 3 を達成することができて、これがあり得る最大値です。
- ウサギ 1 が 4 - 1 = 3 に移動する。
- ウサギ 2 が 2 + 3 = 5 に移動する。
- ウサギ 3 が 4 - 5 = -1 に移動する。
入力例 2
6 2 1 3 2 6 1 5 2 4 3 4 1
出力例 2
4
以下に示すようにそれぞれのウサギが移動すると、ジャンプ後にウサギがいる座標の種類数として 4 を達成することができて、これがあり得る最大値です。
- ウサギ 1 が 2 - 1 = 1 に移動する。
- ウサギ 2 が 3 + 2 = 5 に移動する。
- ウサギ 3 が 6 + 1 = 7 に移動する。
- ウサギ 4 が 5 + 2 = 7 に移動する。
- ウサギ 5 が 4 - 3 = 1 に移動する。
- ウサギ 6 が 4 - 1 = 3 に移動する。
入力例 3
10 1000000000 1000000000 1000000000 1 -1000000000 1000000000 -1000000000 1 0 1 2 1 1 2 4 1 3 2 4 3
出力例 3
9
Score : 500 points
Problem Statement
There are N rabbits numbered 1 to N on a number line. Rabbit i is at coordinate X_i. Multiple rabbits may be at the same coordinate.
Each rabbit has a parameter called jumping power, and rabbit i has jumping power R_i.
Now, all rabbits will jump exactly once. When a rabbit at coordinate x with jumping power r jumps, it moves to coordinate x+r or coordinate x-r.
If you can freely choose which coordinate each rabbit jumps to, find the maximum possible number of distinct coordinates where rabbits are present after all rabbits have jumped.
Constraints
- 1 \leq N \leq 2 \times 10^5
- -10^9 \leq X_i \leq 10^9
- 1 \leq R_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X_1 R_1 X_2 R_2 \vdots X_N R_N
Output
Output the maximum possible number of distinct coordinates where rabbits are present after jumping.
Sample Input 1
3 4 1 2 3 4 5
Sample Output 1
3
If each rabbit moves as shown below, it is possible to achieve 3 as the number of distinct coordinates where rabbits are present after jumping, and this is the maximum possible.
- Rabbit 1 moves to 4 - 1 = 3.
- Rabbit 2 moves to 2 + 3 = 5.
- Rabbit 3 moves to 4 - 5 = -1.
Sample Input 2
6 2 1 3 2 6 1 5 2 4 3 4 1
Sample Output 2
4
If each rabbit moves as shown below, it is possible to achieve 4 as the number of distinct coordinates where rabbits are present after jumping, and this is the maximum possible.
- Rabbit 1 moves to 2 - 1 = 1.
- Rabbit 2 moves to 3 + 2 = 5.
- Rabbit 3 moves to 6 + 1 = 7.
- Rabbit 4 moves to 5 + 2 = 7.
- Rabbit 5 moves to 4 - 3 = 1.
- Rabbit 6 moves to 4 - 1 = 3.
Sample Input 3
10 1000000000 1000000000 1000000000 1 -1000000000 1000000000 -1000000000 1 0 1 2 1 1 2 4 1 3 2 4 3
Sample Output 3
9
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 575 点
問題文
N 個の英小文字からなる文字列 S_1,S_2,\dots,S_N が与えられます。
(1,2,\dots,N) の順列 P=(P_1,P_2,\dots,P_N) としてありえるもの全てについて、以下の通りに生成される文字列を書き並べます。
- S_{P_1},S_{P_2},\dots,S_{P_N} をこの順に連結する。
書き並べられた N! 個の文字列を辞書順に並べた列を A_1,A_2,\dots,A_{N!} とします。
A_2 を出力してください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1 \le T \le 1.5 \times 10^5
- 2 \le N \le 3 \times 10^5
- T,N は整数
- S_i は英小文字からなる長さ 1 以上 10^6-1 以下の文字列
- ひとつの入力について、 N の総和は 3 \times 10^5 を超えない
- ひとつの入力について、全てのテストケースにおける |S_i| の総和は 10^6 を超えない
入力
入力は以下の形式で標準入力から与えられる。
\text{case}_i は i 番目のテストケースを表す。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケースは以下の形式で与えられる。
N S_1 S_2 \vdots S_N
出力
T 行出力せよ。
i 行目には i 番目のテストケースについて、答えを出力せよ。
入力例 1
3 3 abc ac ahc 4 aaa a aaaa a 15 ks sy k ysk yks ky ksy sk syk s kys sky ys yk y
出力例 1
abcahcac aaaaaaaaa kksksykykysskskyssyksyyksykyskyys
この入力には 3 個のテストケースが含まれています。
1 番目のテストケースについて、 S=( abc, ac, ahc ) です。
A=( abcacahc, abcahcac, acabcahc, acahcabc, ahcabcac, ahcacabc ) なので、 A_2= abcahcac を出力します。
Score : 575 points
Problem Statement
You are given N strings S_i consisting of lowercase English letters.
For all possible permutations P=(P_1,P_2,\dots,P_N) of (1,2,\dots,N), write down the string generated as follows:
- Concatenate S_{P_1},S_{P_2},\dots,S_{P_N} in this order.
Let A_1,A_2,\dots,A_{N!} be the sequence of the N! written strings sorted in lexicographical order.
Output A_2.
You are given T test cases; solve each of them.
Constraints
- 1 \le T \le 1.5 \times 10^5
- 2 \le N \le 3 \times 10^5
- T,N are integers.
- S_i is a string consisting of lowercase English letters with length between 1 and 10^6-1, inclusive.
- For a single input, the sum of N does not exceed 3 \times 10^5.
- For a single input, the sum of |S_i| does not exceed 10^6.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case is given in the following format:
N S_1 S_2 \vdots S_N
Output
Output T lines.
The i-th line should contain the answer for the i-th test case.
Sample Input 1
3 3 abc ac ahc 4 aaa a aaaa a 15 ks sy k ysk yks ky ksy sk syk s kys sky ys yk y
Sample Output 1
abcahcac aaaaaaaaa kksksykykysskskyssyksyyksykyskyys
This input contains three test cases.
For the first test case, S=( abc, ac, ahc ).
We have A=( abcacahc, abcahcac, acabcahc, acahcabc, ahcabcac, ahcacabc ), so output A_2= abcahcac.
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 650 点
問題文
1, 2, \dots, 9 および B からなる文字列 A に対して f(A) を次の手順で得られる文字列として定義します。
- はじめ、空文字列 C がある。
- i = 1, 2, \dots, |A| の順に以下の操作を行う。
- A_i が
1,2, \dots,9のいずれかである場合、C の末尾に A_i を追加する。 - A_i =
Bである場合、C の末尾の文字を削除する。ただし C が空文字列である場合は何もしない。
- A_i が
- 上記の操作を全て終了した時点での C を f(A) とする。
1, 2, \dots, 9 および B からなる長さ N の文字列 S が与えられます。
以下で説明される Q 個のクエリを処理してください。クエリは次の 2 種類のいずれかです。
- 1\ \ x\ \ c : S_x を c に更新する。(ここで c は
1,2, \dots,9またはB) - 2\ \ l\ \ r : S の l 文字目から r 文字目までを取り出してできる文字列を T とする。そして U=f(T) とする。U が空文字列の場合は -1 を、そうでない場合は U を 10 進整数とみなした時の値を 998244353 で割った余りを出力せよ。
制約
- 1 \leq N \leq 8 \times 10^6
- 1 \leq Q \leq 2 \times 10^5
- S は
1,2, \dots,9およびBからなる長さ N の文字列 - 1 \leq x \leq N
- c は
1,2, \dots,9またはB - 1 \leq l \leq r \leq N
- N, Q, x, l, r は整数
入力
入力は以下の形式で標準入力から与えられる。ここで \mathrm{query}_i は i 番目のクエリを意味する。
N Q
S
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
クエリは以下の 2 種類のいずれかの形式で与えられる。
1 x c
2 l r
出力
問題文の指示に従ってクエリへの答えを改行区切りで出力せよ。
入力例 1
10 12 1234567891 2 5 7 2 2 8 2 1 10 1 3 B 1 4 B 2 2 4 2 2 8 2 1 10 1 7 B 2 3 9 1 3 4 2 1 10
出力例 1
567 2345678 236323538 -1 5678 567891 589 125891
1 番目のクエリについて、T=U= 567 となります。よって 567 を出力します。
3 番目のクエリについて、T=U= 1234567891 となります。よって 1234567891 \bmod 998244353 = 236323538 を出力します。
6 番目のクエリについて、T= 2BB で U は空文字列となります。よって -1 を出力します。
Score : 650 points
Problem Statement
For a string A consisting of 1, 2, \dots, 9 and B, define f(A) as the string obtained by the following procedure:
- Initially, there is an empty string C.
- Perform the following operations in the order i = 1, 2, \dots, |A|:
- If A_i is one of
1,2, \dots,9, append A_i to the end of C. - If A_i =
B, delete the last character of C. However, if C is an empty string, do nothing.
- If A_i is one of
- Let f(A) be C after completing all the above operations.
You are given a string S of length N consisting of 1, 2, \dots, 9, and B.
Process Q queries described below. Each query is of one of the following two types:
- 1\ \ x\ \ c : Update S_x to c. (Here, c is
1,2, \dots,9, orB.) - 2\ \ l\ \ r : Let T be the string formed by extracting the l-th through r-th characters of S. Then, let U=f(T). If U is an empty string, output -1; otherwise, output the remainder when the value of U regarded as a decimal integer is divided by 998244353.
Constraints
- 1 \leq N \leq 8 \times 10^6
- 1 \leq Q \leq 2 \times 10^5
- S is a string of length N consisting of
1,2, \dots,9, andB. - 1 \leq x \leq N
- c is
1,2, \dots,9, orB. - 1 \leq l \leq r \leq N
- N, Q, x, l, r are integers.
Input
The input is given from Standard Input in the following format, where \mathrm{query}_i denotes the i-th query.
N Q
S
\mathrm{query}_1
\mathrm{query}_2
\vdots
\mathrm{query}_Q
Each query is given in one of the following two formats:
1 x c
2 l r
Output
Output the answers to the queries separated by newlines, following the instructions in the problem statement.
Sample Input 1
10 12 1234567891 2 5 7 2 2 8 2 1 10 1 3 B 1 4 B 2 2 4 2 2 8 2 1 10 1 7 B 2 3 9 1 3 4 2 1 10
Sample Output 1
567 2345678 236323538 -1 5678 567891 589 125891
For the first query, T=U= 567. Thus, output 567.
For the third query, T=U= 1234567891. Thus, output 1234567891 \bmod 998244353 = 236323538.
For the sixth query, T= 2BB and U is an empty string. Thus, output -1.