実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
1 以上 9 以下の数字 A,B,C が与えられます。
A,B,C を好きな順番で並べて繋げることで作れる 3 桁の整数のうち、値が最大のものを求めてください。
制約
- A,B,C は 1 以上 9 以下の数字
入力
入力は以下の形式で標準入力から与えられる。
A B C
出力
答えを出力せよ。
入力例 1
3 2 4
出力例 1
432
A,B,C を好きな順番で並べて繋げることで作れる 3 桁の整数は 324, 342, 234, 243, 432, 423 の 6 通りであり、 このうち値が最大のものは 432 です。
入力例 2
7 7 7
出力例 2
777
777 のみを作ることができます。
入力例 3
9 1 9
出力例 3
991
Score : 100 points
Problem Statement
You are given three digits A,B,C between 1 and 9, inclusive.
Find the maximum value among all 3-digit integers that can be formed by arranging A,B,C in any order and concatenating them.
Constraints
- A,B,C are digits between 1 and 9, inclusive.
Input
The input is given from Standard Input in the following format:
A B C
Output
Output the answer.
Sample Input 1
3 2 4
Sample Output 1
432
There are six 3-digit integers that can be formed by arranging A,B,C in any order and concatenating them: 324, 342, 234, 243, 432, 423; the maximum value among them is 432.
Sample Input 2
7 7 7
Sample Output 2
777
Only 777 can be formed.
Sample Input 3
9 1 9
Sample Output 3
991
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
正整数 X が与えられます。
X を(先頭に 0 を含まない形で)十進表記した際に現れる数字を、先頭に 0 が来ないように 並び替えることで得られる正整数のうち、値が最小のものを求めてください。
制約
- 1\leq X < 10^5
- X は整数
入力
入力は以下の形式で標準入力から与えられる。
X
出力
答えを出力せよ。
入力例 1
903
出力例 1
309
X を十進表記した際に現れる数字を先頭に 0 が来ないように並び替えることで得られる正整数は、903, 930, 309, 390 の 4 通りであり、このうち値が最小のものは 309 です。
入力例 2
432
出力例 2
234
入力例 3
100
出力例 3
100
Score : 200 points
Problem Statement
You are given a positive integer X.
Find the minimum value among all positive integers that can be obtained by rearranging the digits appearing in the decimal representation of X (without leading zeros) such that there is no leading zero.
Constraints
- 1\leq X < 10^5
- X is an integer.
Input
The input is given from Standard Input in the following format:
X
Output
Output the answer.
Sample Input 1
903
Sample Output 1
309
There are four positive integers that can be obtained by rearranging the digits appearing in the decimal representation of X such that there is no leading zero: 903, 930, 309, 390; the minimum value among them is 309.
Sample Input 2
432
Sample Output 2
234
Sample Input 3
100
Sample Output 3
100
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 350 点
問題文
あなたは小さな飴と大きな飴の 2 種類の飴を無尽蔵に持っています。 小さな飴の重量は X グラム、大きな飴の重量は Y グラムであり、小さな飴よりも大きな飴のほうが重い (すなわち、X < Y) です。
N 人の子供がいます。子供たちには 1 から N までの番号が付けられています。
あなたは、以下の条件を満たすように飴を配ることにしました。
- i=1,\dots,N について、子供 i には 2 種類の飴を合計でちょうど A_i 個配る。
- N 人の子供それぞれに配る飴の総重量はすべて等しい。
条件を満たす配り方が存在するかを判定してください。存在する場合はそのような配り方における、大きな飴を配る個数としてあり得る最大値を求めてください。
制約
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i \leq 10^9
- 1 \leq X < Y \leq 10^9
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N X Y A_1 \dots A_N
出力
条件を満たす配り方が存在しない場合、-1 を出力せよ。
条件を満たす配り方が存在する場合、そのような配り方における、大きな飴を配る個数としてあり得る最大値を出力せよ。
入力例 1
3 6 8 11 10 13
出力例 1
18
以下のように飴を配ることで、それぞれの子供に配る飴の総重量がすべて等しくなります。
- 子供 1 には、小さな飴を 4 個、大きな飴を 7 個配る。総重量は 6 \times 4 + 8 \times 7 = 80 グラム。
- 子供 2 には、小さな飴を 0 個、大きな飴を 10 個配る。総重量は 6 \times 0 + 8 \times 10 = 80 グラム。
- 子供 3 には、小さな飴を 12 個、大きな飴を 1 個配る。総重量は 6 \times 12 + 8 \times 1 = 80 グラム。
この配り方では、大きな飴を合計 18 個配っています。
条件を満たす配り方で、18 個より多く大きな飴を配る方法は存在しません。よって、答えは 18 です。
入力例 2
2 3 4 3 5
出力例 2
-1
条件を満たす配り方は存在しません。
入力例 3
8 4 32 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
出力例 3
8000000000
答えは 32bit 整数に収まらないことがあります。
Score : 350 points
Problem Statement
You have an unlimited supply of two types of candies: small candies and large candies. The weight of a small candy is X grams, and the weight of a large candy is Y grams. Large candies are heavier than small candies (that is, X < Y).
There are N children, numbered 1 to N.
You have decided to distribute candies so that the following conditions are satisfied:
- For i=1,\dots,N, child i receives exactly A_i candies in total of the two types.
- The total weights of candies distributed to the N children are all equal.
Determine whether there exists a distribution method that satisfies the conditions. If it exists, find the maximum possible value for the number of large candies distributed.
Constraints
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i \leq 10^9
- 1 \leq X < Y \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N X Y A_1 \dots A_N
Output
If there is no distribution method that satisfies the conditions, output -1.
If there exists a distribution method that satisfies the conditions, output the maximum possible value for the number of large candies distributed in such a distribution method.
Sample Input 1
3 6 8 11 10 13
Sample Output 1
18
You can distribute candies as follows so that the total weights of candies distributed to the children are all equal.
- Child 1 receives 4 small candies and 7 large candies. The total weight is 6 \times 4 + 8 \times 7 = 80 grams.
- Child 2 receives 0 small candies and 10 large candies. The total weight is 6 \times 0 + 8 \times 10 = 80 grams.
- Child 3 receives 12 small candies and 1 large candy. The total weight is 6 \times 12 + 8 \times 1 = 80 grams.
In this distribution method, a total of 18 large candies are distributed.
There is no distribution method that satisfies the conditions and distributes more than 18 large candies. Therefore, the answer is 18.
Sample Input 2
2 3 4 3 5
Sample Output 2
-1
There is no distribution method that satisfies the conditions.
Sample Input 3
8 4 32 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
Sample Output 3
8000000000
The answer may not fit in a 32-bit integer.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
無限に広がる二次元グリッドがあります。マス (x,y) の色は、0 \leq x \leq X-1 かつ 0 \leq y \leq Y-1 ならば黒であり、そうでなければ白です。
このグリッドに対して N 個の大嵐が順に発生します。i 回目の大嵐は、文字 C_i と整数 A_i, B_i で表される法則にしたがって、グリッド上の各マスの色を更新します。
i 回目の大嵐において、大嵐が起きた後のマス (x, y) の色は、
- C_i が
Xの場合、- x < A_i ならば、大嵐が起きる前のマス (x, y + B_i) の色になる。
- x \geq A_i ならば、大嵐が起きる前のマス (x, y - B_i) の色になる。
- C_i が
Yの場合、- y < A_i ならば、大嵐が起きる前のマス (x + B_i, y) の色になる。
- y \geq A_i ならば、大嵐が起きる前のマス (x - B_i, y) の色になる。
2 つの黒いマス (x_1, y_1), (x_2, y_2) が隣接しているとは、|x_1 - x_2| + |y_1 - y_2| = 1 が満たされることを指します。また、2 つの黒いマス c_1, c_2 が連結であるとは、隣接する黒いマスへの移動を繰り返すことでマス c_1 からマス c_2 に移動できることを指します。
空でない黒いマスの集合 S が連結成分であるとは、S が以下の条件を満たすことを指します。
- S に属するどの 2 マスも連結である。
- S に属さないすべての黒いマスが、S に属するどのマスとも連結でない。
N 個の大嵐がすべて発生した後のグリッドについて、連結成分の個数を求め、各連結成分におけるマスの個数を昇順に出力してください。
制約
- N, X, Y は整数
- 1 \leq N \leq 14
- 1 \leq X,Y \leq 10^8
- C_i は
XまたはY - A_i, B_i は整数
- -10^8 \leq A_i, B_i \leq 10^8
入力
入力は以下の形式で標準入力から与えられる。
N X Y C_1 A_1 B_1 \vdots C_N A_N B_N
出力
2 行出力せよ。
1 行目には、黒いマスからなる連結成分の個数を出力せよ。
2 行目には、各連結成分におけるマスの個数を、空白区切りで昇順に出力せよ。
入力例 1
2 3 5 X 2 2 Y -1 1
出力例 1
2 2 13
大嵐によって、グリッドは以下の画像のように変化します(右方向が x 軸の正の向き、上方向が y 軸の正の向き)。
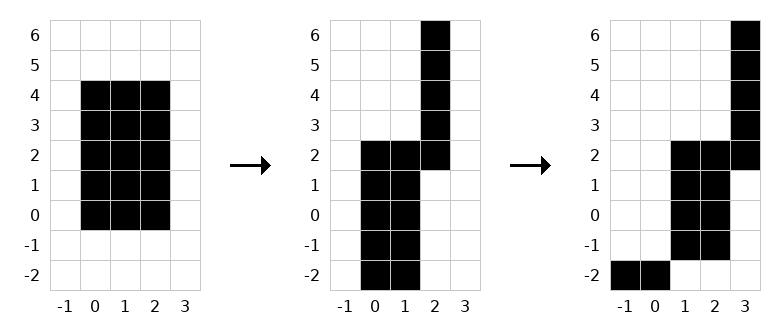
最終的なグリッドにおいて、以下の 2 つの連結成分が存在します。
- マス (-1,-2), (0,-2) からなる連結成分。
- マス (1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6) からなる連結成分。
各連結成分がもつマスの個数は昇順に出力する必要があることに注意してください。
入力例 2
14 68875272 94216928 X 1630731 32914676 X 17164413 -33684569 X 26798060 5418308 X 34094469 -45675954 X 43889566 34125482 X 56836569 -22217058 X 64045210 27857939 Y -54561094 11587606 Y 93548188 32214521 Y -77361096 25750481 Y 27724899 1810420 Y 80945185 -7871305 Y 14782822 -2565089 Y 54687684 -22884393
出力例 2
8 21105046168287 22050167303226 33624667752182 223328231190194 441936776830492 1141371400772596 1141702254882183 3464097998105256
出力する値は 32bit 整数に収まらないことがあります。
Score : 425 points
Problem Statement
There is an infinitely large two-dimensional grid. The color of cell (x,y) is black if 0 \leq x \leq X-1 and 0 \leq y \leq Y-1, and white otherwise.
N great storms occur in order on this grid. The i-th great storm updates the color of each cell on the grid according to a rule represented by a character C_i and integers A_i, B_i.
In the i-th great storm, the color of cell (x, y) after the great storm is:
- In case C_i is
X,- if x < A_i, it becomes the color of cell (x, y + B_i) before the great storm;
- if x \geq A_i, it becomes the color of cell (x, y - B_i) before the great storm.
- In case C_i is
Y,- if y < A_i, it becomes the color of cell (x + B_i, y) before the great storm;
- if y \geq A_i, it becomes the color of cell (x - B_i, y) before the great storm.
Two black cells (x_1, y_1), (x_2, y_2) are adjacent if and only if |x_1 - x_2| + |y_1 - y_2| = 1. Also, two black cells c_1, c_2 are connected if and only if one can move from cell c_1 to cell c_2 by repeatedly moving to adjacent black cells.
A non-empty set S of black cells is a connected component if and only if S satisfies the following conditions:
- Any two cells in S are connected.
- Every black cell not in S is not connected to any cell in S.
For the grid after all N great storms have occurred, find the number of connected components and output the number of cells in each connected component in ascending order.
Constraints
- N, X, Y are integers.
- 1 \leq N \leq 14
- 1 \leq X,Y \leq 10^8
- C_i is
XorY. - A_i, B_i are integers.
- -10^8 \leq A_i, B_i \leq 10^8
Input
The input is given from Standard Input in the following format:
N X Y C_1 A_1 B_1 \vdots C_N A_N B_N
Output
Output two lines.
The first line should contain the number of connected components consisting of black cells.
The second line should contain the number of cells in each connected component, space-separated, in ascending order.
Sample Input 1
2 3 5 X 2 2 Y -1 1
Sample Output 1
2 2 13
The grid changes as shown in the following image due to the great storms (the rightward direction is the positive direction of the x-axis, and the upward direction is the positive direction of the y-axis).

In the final grid, the following two connected components exist:
- A connected component consisting of cells (-1,-2), (0,-2).
- A connected component consisting of cells (1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6).
Note that the number of cells in each connected component must be output in ascending order.
Sample Input 2
14 68875272 94216928 X 1630731 32914676 X 17164413 -33684569 X 26798060 5418308 X 34094469 -45675954 X 43889566 34125482 X 56836569 -22217058 X 64045210 27857939 Y -54561094 11587606 Y 93548188 32214521 Y -77361096 25750481 Y 27724899 1810420 Y 80945185 -7871305 Y 14782822 -2565089 Y 54687684 -22884393
Sample Output 2
8 21105046168287 22050167303226 33624667752182 223328231190194 441936776830492 1141371400772596 1141702254882183 3464097998105256
The output value may not fit in a 32-bit integer.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 450 点
問題文
長さ N の整数列 A=(A_1, A_2, \dots, A_N) が与えられます。
Q 個のクエリが与えられるので、順に処理してください。 各クエリは以下のいずれかの形式です。
1 x y: A_x の値を y に変更する。2 l r: \displaystyle \sum_{1\leq i\leq N} \max(l, \min(r, A_i)) の値を求める。
制約
- 1\leq N \leq 5\times 10^5
- 1\leq Q \leq 2\times 10^5
- 0\leq A_i \leq 5\times 10^5
- 1 種類目のクエリについて、
- 1\leq x\leq N
- 0\leq y \leq 5\times 10^5
- 2 種類目のクエリについて、
- 0\leq l,r \leq 5\times 10^5
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q
A_1 A_2 \dots A_N
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
ここで、\text{query}_i\ (1\leq i\leq Q) は i 番目のクエリを表し、以下のいずれかの形式で与えられる。
1 x y
2 l r
出力
2 種類目のクエリの個数を K として、K 行出力せよ。 i 行目 (1\leq i \leq K) には、2 種類目のクエリのうち i 個目のものに対する答えを出力せよ。
入力例 1
3 4 4 3 2 1 1 7 2 3 5 1 2 0 2 4 2
出力例 1
11 12
はじめ、A=(4,3,2) です。
- 1 番目のクエリ:A_1 の値を 7 に変更します。A=(7,3,2) となります。
- 2 番目のクエリ:\max(3, \min(5, 7))+\max(3, \min(5, 3))+\max(3, \min(5, 2))=5+3+3=11 を出力します。
- 3 番目のクエリ:A_2 の値を 0 に変更します。A=(7,0,2) となります。
- 4 番目のクエリ:\max(4, \min(2, 7))+\max(4, \min(2, 0))+\max(4, \min(2, 2))=4+4+4=12 を出力します。
入力例 2
8 10 320 578 244 604 145 839 156 857 2 400 556 1 5 168 2 254 62 2 145 301 1 1 23 1 3 0 2 413 758 2 297 613 1 8 451 2 598 692
出力例 2
3824 2032 2073 4350 3596 4884
Score : 450 points
Problem Statement
You are given an integer sequence A=(A_1, A_2, \dots, A_N) of length N.
You are given Q queries, which you should process in order. Each query is in one of the following formats:
1 x y: Change the value of A_x to y.2 l r: Find the value of \displaystyle \sum_{1\leq i\leq N} \max(l, \min(r, A_i)).
Constraints
- 1\leq N \leq 5\times 10^5
- 1\leq Q \leq 2\times 10^5
- 0\leq A_i \leq 5\times 10^5
- For queries of the first type,
- 1\leq x\leq N
- 0\leq y \leq 5\times 10^5
- For queries of the second type,
- 0\leq l,r \leq 5\times 10^5
- All inputs are integers.
Input
The input is given from Standard Input in the following format:
N Q
A_1 A_2 \dots A_N
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
Here, \text{query}_i\ (1\leq i\leq Q) represents the i-th query and is given in one of the following formats:
1 x y
2 l r
Output
Let K be the number of queries of the second type. Output K lines. The i-th line (1\leq i \leq K) should contain the answer to the i-th query of the second type.
Sample Input 1
3 4 4 3 2 1 1 7 2 3 5 1 2 0 2 4 2
Sample Output 1
11 12
Initially, A=(4,3,2).
- First query: Change the value of A_1 to 7. A becomes (7,3,2).
- Second query: Output \max(3, \min(5, 7))+\max(3, \min(5, 3))+\max(3, \min(5, 2))=5+3+3=11.
- Third query: Change the value of A_2 to 0. A becomes (7,0,2).
- Fourth query: Output \max(4, \min(2, 7))+\max(4, \min(2, 0))+\max(4, \min(2, 2))=4+4+4=12.
Sample Input 2
8 10 320 578 244 604 145 839 156 857 2 400 556 1 5 168 2 254 62 2 145 301 1 1 23 1 3 0 2 413 758 2 297 613 1 8 451 2 598 692
Sample Output 2
3824 2032 2073 4350 3596 4884
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 525 点
問題文
N 人の子供がいます。子供たちには 1 から N までの番号が付けられています。
子供 i は飴を A_i 個持っています。
あなたの目標は、以下の操作をできるだけ少ない回数実行し、最終的に N 人の子供全員が同数の飴を持っている状態にすることです。
- 相異なる 2 人の子供 x,y を選び、子供 x が持っている飴の個数以下の正の整数 z を選ぶ。子供 x が持っている飴のうち z 個を回収し、子供 y に渡す。
最終的に N 人の子供全員が同数の飴を持っている状態になる操作列が存在するか判定してください。存在する場合は、そのうち操作回数が最小になるようなものを 1 つ求めてください。
制約
- 2 \leq N \leq 20
- 1 \leq A_i \leq 10^8
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 \dots A_N
出力
最終的に N 人の子供全員が同数の飴を持っている状態になる操作列が存在しない場合、-1 を出力せよ。
存在する場合、そのうち操作回数が最小になるものを以下の形式で出力せよ。
q x_1 y_1 z_1 \vdots x_q y_q z_q
ここで、q は操作回数を表し、x_i,y_i,z_i は i 回目の操作で選ぶ x,y,z の値を表す。
解が複数存在するときは、どれを出力しても正解とみなされる。
入力例 1
4 1 7 4 8
出力例 1
3 2 3 1 2 4 1 4 1 4
この出力例では、以下のように操作が実行されます。
- 子供 2 から飴を 1 個回収し、子供 3 に渡す。この直後、各子供が持つ飴の個数は 1,6,5,8 になっている。
- 子供 2 から飴を 1 個回収し、子供 4 に渡す。この直後、各子供が持つ飴の個数は 1,5,5,9 になっている。
- 子供 4 から飴を 4 個回収し、子供 1 に渡す。この直後、各子供が持つ飴の個数は 5,5,5,5 になっている。
これによって、最終的に N 人の子供全員が飴をちょうど 5 個ずつ持っている状態になります。
入力例 2
2 100 3
出力例 2
-1
Score : 525 points
Problem Statement
There are N children, numbered 1 to N.
Child i has A_i candies.
Your goal is to execute the following operation as few times as possible so that eventually all N children have the same number of candies.
- Choose two distinct children x,y, and choose a positive integer z not exceeding the number of candies child x has. Take z candies from child x and give them to child y.
Determine whether there exists a sequence of operations such that eventually all N children have the same number of candies. If it exists, find one such sequence with the minimum number of operations.
Constraints
- 2 \leq N \leq 20
- 1 \leq A_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 \dots A_N
Output
If there is no sequence of operations such that eventually all N children have the same number of candies, output -1.
If it exists, output one with the minimum number of operations in the following format:
q x_1 y_1 z_1 \vdots x_q y_q z_q
Here, q represents the number of operations, and x_i,y_i,z_i represent the values of x,y,z chosen in the i-th operation.
If there are multiple solutions, outputting any of them will be considered correct.
Sample Input 1
4 1 7 4 8
Sample Output 1
3 2 3 1 2 4 1 4 1 4
In this sample output, the operations are executed as follows:
- Take 1 candy from child 2 and give it to child 3. Immediately after this, the number of candies each child has is 1,6,5,8.
- Take 1 candy from child 2 and give it to child 4. Immediately after this, the number of candies each child has is 1,5,5,9.
- Take 4 candies from child 4 and give them to child 1. Immediately after this, the number of candies each child has is 5,5,5,5.
Eventually, all N children have exactly five candies each.
Sample Input 2
2 100 3
Sample Output 2
-1
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 575 点
問題文
長さ N の正整数列 A=(A_1,A_2,\dots,A_N) および長さ M の正整数列 B=(B_1,B_2,\dots,B_M) が与えられます。
\displaystyle \sum_{i=1}^{N} \sum_{j=1}^{M} \binom{A_i}{B_j} の値を 998244353 で割った余りを求めてください。
ここで、\displaystyle \binom{x}{y} は x 個のものの中から y 個のものを選ぶ場合の数(二項係数)を表し、特に x < y のときは 0 です。
制約
- 1\leq N,M \leq 5\times 10^5
- 1\leq A_i,B_j \leq 5\times 10^5
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 \dots A_N B_1 B_2 \dots B_M
出力
答えを出力せよ。
入力例 1
3 2 2 5 4 1 3
出力例 1
25
答えは \displaystyle \binom{2}{1}+\binom{2}{3}+\binom{5}{1}+\binom{5}{3}+\binom{4}{1}+\binom{4}{3}=2+0+5+10+4+4=25 です。
入力例 2
4 4 2 5 1 5 2 1 2 4
出力例 2
65
入力例 3
6 8 203497 47202 407775 394325 463982 304784 468417 302156 131932 235902 395728 78537 223857 330739
出力例 3
602855848
Score : 575 points
Problem Statement
You are given a sequence of positive integers A=(A_1,A_2,\dots,A_N) of length N and a sequence of positive integers B=(B_1,B_2,\dots,B_M) of length M.
Find the value of \displaystyle \sum_{i=1}^{N} \sum_{j=1}^{M} \binom{A_i}{B_j}, modulo 998244353.
Here, \displaystyle \binom{x}{y} represents the number of ways to choose y objects from x objects (binomial coefficient), and particularly, it is 0 if x < y.
Constraints
- 1\leq N,M \leq 5\times 10^5
- 1\leq A_i,B_j \leq 5\times 10^5
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 A_2 \dots A_N B_1 B_2 \dots B_M
Output
Output the answer.
Sample Input 1
3 2 2 5 4 1 3
Sample Output 1
25
The answer is \displaystyle \binom{2}{1}+\binom{2}{3}+\binom{5}{1}+\binom{5}{3}+\binom{4}{1}+\binom{4}{3}=2+0+5+10+4+4=25.
Sample Input 2
4 4 2 5 1 5 2 1 2 4
Sample Output 2
65
Sample Input 3
6 8 203497 47202 407775 394325 463982 304784 468417 302156 131932 235902 395728 78537 223857 330739
Sample Output 3
602855848