実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
面積が正である三角形 ABC があります。
三角形 ABC の三辺の長さはそれぞれ a,b,c です。
三角形 ABC が二等辺三角形であるか判定してください。
制約
- 1 \leq a,b,c \leq 10
- 三辺の長さが a,b,c であるような三角形が存在し、その面積は正である。
- a,b,c は整数
入力
入力は以下の形式で標準入力から与えられる。
a b c
出力
三角形 ABC が二等辺三角形であるならば Yes を、そうでないならば No を出力せよ。
入力例 1
4 2 4
出力例 1
Yes
a=c であるため、三角形 ABC は二等辺三角形です。
よって、Yes を出力します。
入力例 2
3 4 5
出力例 2
No
三角形 ABC の三辺の長さはすべて異なるため、二等辺三角形ではありません。
よって、No を出力します。
入力例 3
10 10 10
出力例 3
Yes
正三角形も二等辺三角形の一種であることに注意してください。
Score : 100 points
Problem Statement
There is a triangle ABC with positive area.
The lengths of the three sides of triangle ABC are a,b,c.
Determine whether triangle ABC is isosceles.
Constraints
- 1 \leq a,b,c \leq 10
- A triangle with side lengths a,b,c exists, and its area is positive.
- a,b,c are integers.
Input
The input is given from Standard Input in the following format:
a b c
Output
If triangle ABC is isosceles, output Yes; otherwise, output No.
Sample Input 1
4 2 4
Sample Output 1
Yes
Since a=c, triangle ABC is isosceles.
Thus, output Yes.
Sample Input 2
3 4 5
Sample Output 2
No
Since the three side lengths of triangle ABC are all different, it is not isosceles.
Thus, output No.
Sample Input 3
10 10 10
Sample Output 3
Yes
Note that an equilateral triangle is a kind of isosceles triangle.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
N 人の人が、M 問からなるプログラミングコンテストに参加しました。
参加者は人 1, 人 2, \ldots, 人 N と番号づけられており、問題は問題 1, 問題 2, \ldots, 問題 M と番号づけられています。
このコンテストでは K 個のイベントが順番に起き、i 番目 (1\leq i\leq K) のイベントでは次のことが起きました。
- 人 A_i が問題 B_i に正解した。
同じイベントが 2 回以上起きることはありません。 また、この K 個のイベント以外に誰かがどれかの問題に正解することはありません。
すべての問題に正解した人の番号を全員出力してください。
そのような人が複数いる場合は、すべての問題に正解したタイミングが早い順に出力してください。
制約
- 1 \leq N \leq 10
- 1 \leq M \leq 10
- K \geq 1
- 1 \leq A_i\leq N
- 1 \leq B_i\leq M
- i\neq j ならば (A_i,B_i)\neq (A_j,B_j)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M K A_1 B_1 A_2 B_2 \vdots A_K B_K
出力
すべての問題に正解した人の番号を、すべての問題に正解したタイミングが早い順に空白区切りで一行に出力せよ。
すべての問題に正解した人がいないならば、何も出力しないようにせよ。
入力例 1
3 2 5 1 1 3 2 2 1 3 1 1 2
出力例 1
3 1
コンテストでは次のことが順に起きました。
- 人 1 が問題 1 に正解した。人 1 はこれまでに、問題 1 のみに正解した。
- 人 3 が問題 2 に正解した。人 3 はこれまでに、問題 2 のみに正解した。
- 人 2 が問題 1 に正解した。人 2 はこれまでに、問題 1 のみに正解した。
- 人 3 が問題 1 に正解した。人 3 はこれまでに、問題 1,2 に正解した。よって、この時点で人 3 はすべての問題に正解した。
- 人 1 が問題 2 に正解した。人 1 はこれまでに、問題 1,2 に正解した。よって、この時点で人 1 はすべての問題に正解した。
よって、すべての問題に正解したのは人 1,3 であり、すべての問題に正解したタイミングは人 3 の方が早いです。
よって、3,1 をこの順に空白区切りで出力します。
入力例 2
2 2 2 1 1 2 2
出力例 2
すべての問題に正解した人がいない場合は、何も出力しないでください。
Score : 200 points
Problem Statement
N people participated in a programming contest consisting of M problems.
The participants are numbered person 1, person 2, \ldots, person N, and the problems are numbered problem 1, problem 2, \ldots, problem M.
In this contest, K events occurred in order; in the i-th event (1\leq i\leq K), the following happened:
- Person A_i solved problem B_i.
The same event does not occur two or more times. Also, apart from these K events, nobody solves any problem.
Output the numbers of all people who solved all problems.
If there are multiple such people, output them in ascending order of the time at which they solved all problems.
Constraints
- 1 \leq N \leq 10
- 1 \leq M \leq 10
- K \geq 1
- 1 \leq A_i \leq N
- 1 \leq B_i \leq M
- If i\neq j then (A_i,B_i)\neq (A_j,B_j).
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M K A_1 B_1 A_2 B_2 \vdots A_K B_K
Output
Output, on one line and separated by spaces, the numbers of all people who solved all problems, in ascending order of the time at which they solved all problems. If there is no person who solved all problems, output nothing.
Sample Input 1
3 2 5 1 1 3 2 2 1 3 1 1 2
Sample Output 1
3 1
In the contest, the following happened in order.
- Person 1 solved problem 1. So far, person 1 has solved only problem 1.
- Person 3 solved problem 2. So far, person 3 has solved only problem 2.
- Person 2 solved problem 1. So far, person 2 has solved only problem 1.
- Person 3 solved problem 1. So far, person 3 has solved problems 1,2. Thus, at this point person 3 has solved all problems.
- Person 1 solved problem 2. So far, person 1 has solved problems 1,2. Thus, at this point person 1 has solved all problems.
Thus, the people who solved all problems are persons 1,3, and the one who solved all problems earlier is person 3. Thus, output 3,1 in this order, separated by spaces.
Sample Input 2
2 2 2 1 1 2 2
Sample Output 2
If there is no person who solved all problems, output nothing.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
高橋君はゲームをしています。このゲームには 1 から N の番号がついた N 個のスキルがあります。
N 個の整数の組 (A_1,B_1), \dots,(A_N,B_N) が与えられます。
(A_i,B_i)=(0,0) のとき高橋君はスキル i を習得済みです。
そうでないとき、スキル A_i,B_i の少なくとも一方を習得済みのときかつそのときに限りスキル i を習得することができます。
既に取得済みのスキルも含め、高橋君が最終的に習得することができるスキルの個数を求めてください。
制約
- 1\leq N \leq 2\times 10^5
- (A_i,B_i)=(0,0) または 1\leq A_i,B_i \leq N
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
答えを出力せよ。
入力例 1
6 0 0 1 3 3 2 5 5 4 6 6 4
出力例 1
3
最初、高橋君はスキル 1 を習得済みです。スキル 1 を習得済みのためスキル 2 を習得することができ、スキル 2 を習得したことでスキル 3 を習得できます。
スキル 4,5,6 を習得することはできないため、答えは 3 となります。
入力例 2
4 0 0 0 0 0 0 0 0
出力例 2
4
Score : 300 points
Problem Statement
Takahashi is playing a game. This game has N skills numbered 1 through N.
You are given N pairs of integers (A_1,B_1), \dots,(A_N,B_N).
If (A_i,B_i)=(0,0), then Takahashi has already learned skill i.
Otherwise, Takahashi can learn skill i if and only if at least one of skills A_i and B_i has already been learned.
Including the skills already learned, find the number of skills that Takahashi can ultimately learn.
Constraints
- 1\leq N \leq 2\times 10^5
- (A_i,B_i)=(0,0) or 1\leq A_i,B_i \leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Output the answer.
Sample Input 1
6 0 0 1 3 3 2 5 5 4 6 6 4
Sample Output 1
3
At first, Takahashi has already learned skill 1. Because skill 1 has been learned, skill 2 can be learned, and learning skill 2 enables learning skill 3. Since it is impossible to learn skills 4,5,6, the answer is 3.
Sample Input 2
4 0 0 0 0 0 0 0 0
Sample Output 2
4
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
H 行 W 列のマス目があり、各マスは白または黒に塗られています。
マス目の上から i 番目 (1\leq i\leq H) かつ左から j 番目 (1\leq j\leq W) のマスをマス (i,j) と表すことにします。
マス目の状態は H 個の、. と # のみからなる長さ W の文字列 S_1,S_2,\ldots,S_H によって与えられ、
S_i の j 文字目が . のとき、マス (i,j) が白く塗られていることを、# のときマス (i,j) が黒く塗られていることを表します。
高橋君はいくつか(0 個でも良い)の黒く塗られたマスを白に塗り替えることで、 マス目が黒く塗られたマスのみからなる 2\times 2 の部分を持たないようにしたいです。 より厳密には、次の条件をみたすようにしたいです。
1\leq i\leq H-1, 1\leq j\leq W-1 をみたす任意の整数の組 (i,j) について、 マス (i,j), マス (i,j+1), マス (i+1,j), マス (i+1,j+1) のうち 少なくとも 1 つは白く塗られている 。
高橋君が目標を達成するために、白く塗り替える必要のあるマスの個数の最小値を求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1\leq T\leq 100
- 2\leq H\leq 7
- 2\leq W\leq 7
- S_i は
.と#のみからなる長さ W の文字列 - T,H,W は整数
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
\mathrm{case}_i は i 番目のテストケースを表す。 各テストケースは以下の形式で与えられる。
H W S_1 S_2 \vdots S_H
出力
T 行出力せよ。
i 行目 (1\leq i\leq T) には、i 個目のテストケースの答えを出力せよ。
入力例 1
2 5 5 ####. ##.## ##### .#### ##.#. 2 2 .. ..
出力例 1
3 0
1 つめのテストケースについて、マス目の最初の状態は、下図左のようになっています。
このマス目の黒いマスのうち、例えば下図右の番号が入っている 3 つのマスを白く塗り替えることで、条件をみたすようにできます。

最初の状態から 2 個以下のマスを白く塗ることで条件をみたすようにすることはできないため、3 を 1 行目に出力します。
2 つめのテストケースについて、マス目は最初から条件をみたしています。
よって、0 を 2 行目に出力します。
Score : 425 points
Problem Statement
There is a grid with H rows and W columns, and each cell is painted white or black.
Let us denote the cell at the i-th row from the top (1\leq i\leq H) and the j-th column from the left (1\leq j\leq W) by cell (i,j).
The state of the grid is given by H strings S_1,S_2,\ldots,S_H of length W consisting of . and #.
If the j-th character of S_i is ., then cell (i,j) is white; if it is #, then cell (i,j) is black.
By repainting some black cells (possibly zero) to white, Takahashi wants to make the grid have no 2\times 2 subgrid consisting only of black cells. More precisely, he wants to satisfy the following condition.
For any integer pair (i,j) with 1\leq i\leq H-1 and 1\leq j\leq W-1, among cells (i,j), (i,j+1), (i+1,j), and (i+1,j+1), at least one is white.
Find the minimum number of cells that need to be repainted white in order for Takahashi to achieve his goal.
You are given T test cases; answer each of them.
Constraints
- 1\leq T\leq 100
- 2\leq H\leq 7
- 2\leq W\leq 7
- Each S_i is a string of length W consisting of
.and#. - T,H,W are integers.
Input
The input is given from Standard Input in the following format:
T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T
\mathrm{case}_i represents the i-th test case. Each test case is given in the following format:
H W S_1 S_2 \vdots S_H
Output
Output T lines. On the i-th line (1\leq i\leq T), output the answer for the i-th test case.
Sample Input 1
2 5 5 ####. ##.## ##### .#### ##.#. 2 2 .. ..
Sample Output 1
3 0
For the first test case, the initial state of the grid is as shown in the left figure below. By repainting, for example, the three cells with numbers in the right figure below from black to white, the condition can be satisfied.

It is impossible to satisfy the condition by repainting two or fewer cells from the initial state, so output 3 on the 1-st line.
For the second test case, the grid already satisfies the condition from the beginning. Thus, output 0 on the 2-nd line.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 475 点
問題文
長さが A_1,\ldots,A_N の N 本の棒が袋に入っています。
あなたは次の操作を K 回繰り返します。
- 袋に入っている棒の中で最も長いものを 1 本取り出し、二等分して、2 本の棒を袋に戻す
K 回の操作が終わった後、袋の中にある N+K 本の棒のうち、長い方から X 番目のものの長さを求めてください。
T 個のテストケースが与えられるので、それぞれについて答えてください。
制約
- 1 \leq T \leq 10^5
- それぞれのテストケースについて、
- 1 \leq N \leq 10^5
- 1 \leq A_i \leq 10^9
- 1 \leq K \leq 10^9
- 1 \leq X \leq N+K
- 全てのテストケースについての N の総和は 10^5 を超えない
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{testcase}_1
\mathrm{testcase}_2
\vdots
\mathrm{testcase}_T
\mathrm{testcase}_i は i 番目のテストケースを表し、次の形式で与えられる。
N K X A_1 \ldots A_N
出力
T 行出力せよ。i 行目 (1 \leq i \leq T) には i 番目のテストケースに対する答えを出力せよ。
真の解との絶対誤差または相対誤差が 10^{-9} 以下のとき正解と判定される。
入力例 1
2 3 4 5 40 20 30 10 100 50 1 2 3 4 5 6 7 8 9 10
出力例 1
10.00000000000000000000 0.50000000000000000000
1 番目のテストケースでは、最初、袋の中には長さが 20,30,40 の 3 本の棒が入っています。操作は次のように進行します。
- 長さ 40 の棒を袋から取り出し、長さ 20 の棒 2 本を袋に戻す。袋の中の棒の長さは 20,20,20,30 となる。
- 長さ 30 の棒を袋から取り出し、長さ 15 の棒 2 本を袋に戻す。袋の中の棒の長さは 15,15,20,20,20 となる。
- 長さ 20 の棒を袋から取り出し、長さ 10 の棒 2 本を袋に戻す。袋の中の棒の長さは 10,10,15,15,20,20 となる。
- 長さ 20 の棒を袋から取り出し、長さ 10 の棒 2 本を袋に戻す。袋の中の棒の長さは 10,10,10,10,15,15,20 となる。
操作後に長い方から 5 番目の棒の長さは 10 です。
Score : 475 points
Problem Statement
There are N sticks in a bag, with lengths A_1,\ldots,A_N.
You repeat the following operation K times.
- Take out any one of the longest sticks in the bag, split it into two equal halves, and put the two sticks back into the bag.
After K operations, among the N+K sticks in the bag, find the length of the X-th longest one.
You are given T test cases; answer each of them.
Constraints
- 1 \leq T \leq 10^5
- For each test case:
- 1 \leq N \leq 10^5
- 1 \leq A_i \leq 10^9
- 1 \leq K \leq 10^9
- 1 \leq X \leq N+K
- The sum of N over all test cases does not exceed 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\mathrm{testcase}_1
\mathrm{testcase}_2
\vdots
\mathrm{testcase}_T
\mathrm{testcase}_i represents the i-th test case and is given in the following format:
N K X A_1 \ldots A_N
Output
Print T lines. In the i-th line (1 \leq i \leq T), output the answer for the i-th test case.
Your answer will be judged correct if the absolute or relative error is at most 10^{-9}.
Sample Input 1
2 3 4 5 40 20 30 10 100 50 1 2 3 4 5 6 7 8 9 10
Sample Output 1
10.00000000000000000000 0.50000000000000000000
In the 1-st test case, initially the bag contains 3 sticks of lengths 20,30,40. The operations proceed as follows.
- Take out the stick of length 40 from the bag, split it into two sticks of length 20, and put them back. The stick lengths in the bag become 20,20,20,30.
- Take out the stick of length 30 from the bag, split it into two sticks of length 15, and put them back. The stick lengths in the bag become 15,15,20,20,20.
- Take out a stick of length 20 from the bag, split it into two sticks of length 10, and put them back. The stick lengths in the bag become 10,10,15,15,20,20.
- Take out a stick of length 20 from the bag, split it into two sticks of length 10, and put them back. The stick lengths in the bag become 10,10,10,10,15,15,20.
After the operations, the 5-th longest stick has length 10.
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 525 点
問題文
円周上に等間隔に N 個の点があり、時計回りに 1,2,\dots,N と番号がついています。
以下の形式のクエリが Q 個与えられるので順に処理してください。
- 点 A_i と点 B_i を結ぶ線分を書く。ただし、この線分が既に書かれている線分と交わる場合は書かない。
ここで、2Q 個の整数 A_1,\ldots,A_Q,B_1,\ldots,B_Q は相異なることが保証されます。
各線分が書かれたかどうか答えてください。
制約
- 2 \leq N \leq 10^6
- 1 \leq Q \leq 3\times 10^5
- 1 \leq A_i < B_i \leq N
- 2Q 個の整数 A_1,\ldots,A_Q,B_1,\ldots,B_Q は相異なる
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q A_1 B_1 A_2 B_2 \vdots A_Q B_Q
出力
Q 行出力せよ。
i 行目には、i 番目のクエリにおいて線分が書かれたとき Yes、書かれなかったとき No と出力せよ。
入力例 1
8 3 1 5 2 7 3 4
出力例 1
Yes No Yes
クエリにより図のように線分が書かれます。
- 1 番目のクエリで、点 1 と点 5 を結ぶ線分が書かれる。
- 2 番目のクエリで、点 2 と点 7 を結ぶ線分は、1 番目のクエリで書いた線分と交わるので書かない。
- 3 番目のクエリで、点 3 と点 4 を結ぶ線分が書かれる。
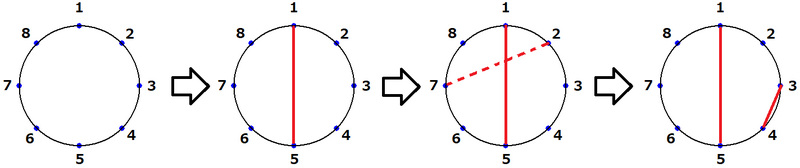
入力例 2
999999 4 123456 987654 888888 999999 1 3 2 777777
出力例 2
Yes No Yes No
Score : 525 points
Problem Statement
There are N points equally spaced on a circle, numbered 1,2,\dots,N clockwise.
You are given Q queries of the following form; process them in order.
- Draw the line segment connecting points A_i and B_i. However, if this segment intersects a segment that has already been drawn, do not draw it.
Here, it is guaranteed that the 2Q integers A_1,\ldots,A_Q,B_1,\ldots,B_Q are all distinct.
For each query, answer whether the segment was drawn.
Constraints
- 2 \leq N \leq 10^6
- 1 \leq Q \leq 3\times 10^5
- 1 \leq A_i < B_i \leq N
- The 2Q integers A_1,\ldots,A_Q,B_1,\ldots,B_Q are pairwise distinct.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q A_1 B_1 A_2 B_2 \vdots A_Q B_Q
Output
Output Q lines.
On the i-th line, output Yes if, in the i-th query, the segment was drawn, and No if it was not drawn.
Sample Input 1
8 3 1 5 2 7 3 4
Sample Output 1
Yes No Yes
By the queries, the segments are drawn as in the figure.
- In the 1-st query, the segment connecting points 1 and 5 is drawn.
- In the 2-nd query, the segment connecting points 2 and 7 is not drawn because it intersects the segment drawn in the 1-st query.
- In the 3-rd query, the segment connecting points 3 and 4 is drawn.

Sample Input 2
999999 4 123456 987654 888888 999999 1 3 2 777777
Sample Output 2
Yes No Yes No
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 625 点
問題文
アイドル 1, アイドル 2, \ldots, アイドル N の N 人のアイドルからなるグループがあります。
また、曲の候補が M 曲あり、それぞれ曲 1, 曲 2, \ldots, 曲 M と番号づけられています。
高橋君は、これらのうちから何曲か(0 曲でも良い)を選びライブを行いたいと考えています。
ただし、同じ曲は 1 回までしか選ぶことはできません。
アイドル i (1\leq i\leq N) は A_i 曲まで踊ることができます。
また、ライブにおいて、曲 j (1\leq j\leq M) では B_j 人のアイドルが踊る必要があり、(誰が踊ったかによらず)その曲の盛り上がりは C_j です。
高橋君は、それぞれのアイドルが踊れる回数を超えないように、 ライブで演奏する曲およびそれぞれの曲で踊るアイドルを選びます。 選んだ曲の盛り上がりの総和としてあり得る最大値を求めてください。
制約
- 1\leq N\leq 100
- 1\leq M\leq 100
- 0\leq A_i\leq M
- 0\leq B_i\leq N
- 0\leq C_i\leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 A_2 \ldots A_N B_1 C_1 B_2 C_2 \vdots B_M C_M
出力
高橋君が選んだ曲の盛り上がりの総和としてあり得る最大値を出力せよ。
入力例 1
3 3 1 1 3 1 1 2 5 3 10
出力例 1
11
例えば、曲 1,3 を選んで次のように踊るアイドルを選ぶことができます。
- 曲 1 では、アイドル 3 のみが踊る。
- 曲 3 では、アイドル 1,2,3 が踊る。
このとき、アイドル 1,2,3 が踊る曲数はそれぞれ 1,1,2 であり、条件をみたしています。
このとき、選んだ曲の盛り上がりの総和は 1+10=11 となります。
条件をみたしつつこれより盛り上がりの総和が大きくなるように曲を選ぶことはできないため、 11 を出力します。
入力例 2
2 6 6 0 0 1000000000 0 1000000000 1 1000000000 1 1000000000 1 1000000000 2 1000000000
出力例 2
5000000000
例えば、曲 1,2,3,4,5 を選んで、次のように踊るアイドルを選ぶことができます。
- 曲 1 では、誰も踊らない。
- 曲 2 では、誰も踊らない。
- 曲 3 では、アイドル 1 のみが踊る。
- 曲 4 では、アイドル 1 のみが踊る。
- 曲 5 では、アイドル 1 のみが踊る。
このとき選んだ曲の盛り上がりの総和は 5000000000 となり、これが最大となります。
Score : 625 points
Problem Statement
There is a group of N idols: idol 1, idol 2, \ldots, idol N.
There are M candidate songs, numbered song 1, song 2, \ldots, song M.
Takahashi wants to select some of these songs (possibly 0) and hold a live performance.
However, the same song can be selected at most once.
Idol i (1\leq i\leq N) can dance up to A_i songs.
In the live performance, song j (1\leq j\leq M) requires B_j idols to dance, and (regardless of who dances) the excitement of that song is C_j.
Takahashi selects the songs to be performed and, for each selected song, the idols who will dance, without exceeding each idol’s allowed number of dances. Find the maximum possible sum of excitement of the selected songs.
Constraints
- 1\leq N\leq 100
- 1\leq M\leq 100
- 0\leq A_i\leq M
- 0\leq B_i\leq N
- 0\leq C_i\leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 A_2 \ldots A_N B_1 C_1 B_2 C_2 \vdots B_M C_M
Output
Output the maximum possible sum of excitement of the songs that Takahashi selects.
Sample Input 1
3 3 1 1 3 1 1 2 5 3 10
Sample Output 1
11
For example, he can select songs 1,3 and choose the dancers as follows.
- In song 1, only idol 3 dances.
- In song 3, idols 1,2,3 dance.
Then, the numbers of songs danced by idols 1,2,3 are 1,1,2, respectively, and the conditions are satisfied. Here, the sum of excitement of the selected songs is 1+10=11.
It is impossible to select songs so that the sum of excitement becomes larger while satisfying the conditions, so output 11.
Sample Input 2
2 6 6 0 0 1000000000 0 1000000000 1 1000000000 1 1000000000 1 1000000000 2 1000000000
Sample Output 2
5000000000
For example, he can select songs 1,2,3,4,5 and choose the dancers as follows.
- In song 1, nobody dances.
- In song 2, nobody dances.
- In song 3, only idol 1 dances.
- In song 4, only idol 1 dances.
- In song 5, only idol 1 dances.
Then, the sum of excitement of the selected songs is 5000000000, and this is maximum.