AtCoder Beginner Contest 404（Promotion for Engineer Guild）

A - Not Found

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 100 点

問題文

英小文字からなる長さ 1 以上 25 以下の文字列 S が与えられます。
S に含まれない英小文字をひとつ出力してください。
但し、そのようなものが複数ある場合はどれを出力しても構いません。

制約

S は英小文字からなる長さ 1 以上 25 以下の文字列

入力

入力は以下の形式で標準入力から与えられる。

出力

S に含まれない英小文字をひとつ出力せよ。そのようなものが複数ある場合はどれを出力しても構わない。

入力例 1

出力例 1

S= a です。
a 以外の英小文字、 b, c, ..., z が正解となります。

入力例 2

abcdfhijklmnopqrstuvwxyz

出力例 2

S 中に含まれない英小文字は e と g です。

入力例 3

qazplwsxokmedcijnrfvuhbgt

出力例 3

Score : 100 points

Problem Statement

You are given a string S of length between 1 and 25 consisting of lowercase English letters.
Output one lowercase English letter that does not appear in S.
If there are multiple such letters, you may output any one of them.

Constraints

S is a string of length between 1 and 25 (inclusive) consisting of lowercase English letters.

Input

The input is given from Standard Input in the following format:

Output

Output one lowercase English letter that does not appear in S. If there are multiple such letters, you may output any one of them.

Sample Input 1

Sample Output 1

S= a.
Any lowercase English letter other than a (that is, b, c, …, or z) is a correct answer.

Sample Input 2

abcdfhijklmnopqrstuvwxyz

Sample Output 2

The lowercase English letters not included in S are e and g.

Sample Input 3

qazplwsxokmedcijnrfvuhbgt

Sample Output 3

B - Grid Rotation

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 250 点

問題文

縦 N 行横 N 列からなる 2 つのグリッド S,T があります。グリッドの上から i 行目、左から j 列目のマスをマス (i,j) と表します。

グリッド S,T の各マスは白または黒のいずれかに塗られています。S_{i,j} が . のとき S のマス (i,j) は白く、S_{i,j} が # のとき S のマス (i,j) は黒く塗られています。T についても同様です。

次の 2 種類の操作を好きな順序で好きな回数行うとき、グリッド S をグリッド T と一致させるために必要な操作回数の最小値を求めてください。

グリッド S のマスを 1 つ選び、色を変更する
グリッド S 全体を 90 度右に回転する

制約

1\leq N \leq 100
N は整数
S_{i,j},T_{i,j} は . または #

入力

入力は以下の形式で標準入力から与えられる。

N
S_{1,1}S_{1,2}\dots S_{1,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,N}
\vdots
T_{N,1}T_{N,2}\dots T_{N,N}

出力

答えを出力せよ。

入力例 1

4
###.
..#.
..#.
..#.
...#
...#
###.
....

出力例 1

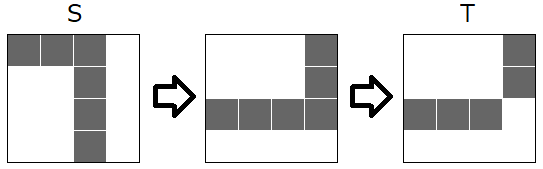
下図のようにして 2 回の操作で S を T と一致させることができます。

入力例 2

13
.#..###..##..
#.#.#..#.#.#.
#.#.###..#...
###.#..#.#.#.
#.#.###..##..
.............
..#...#....#.
.##..#.#..##.
#.#..#.#.#.#.
####.#.#.####
..#..#.#...#.
..#...#....#.
.............
.............
.#....#...#..
.#...#.#..#..
####.#.#.####
.#.#.###..#.#
.##....#..##.
.#....#...#..
.............
..##..###.#.#
.#.#.#..#.###
.#.#..###.#.#
.#.#.#..#.#.#
..##..###..#.

出力例 2

Score : 250 points

Problem Statement

There are two grids S and T, each with N rows and N columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.

Each cell of grids S and T is colored either white or black. Cell (i,j) of S is white if S_{i,j} is ., and black if S_{i,j} is #. The same applies to T.

You may perform the following two types of operations any number of times in any order. Find the minimum number of operations required to make grid S identical to grid T.

Choose one cell of grid S and change its color.
Rotate the entire grid S 90 degrees clockwise.

Constraints

1 \le N \le 100
N is an integer.
Each of S_{i,j} and T_{i,j} is . or #.

Input

The input is given from Standard Input in the following format:

N
S_{1,1}S_{1,2}\dots S_{1,N}
\vdots
S_{N,1}S_{N,2}\dots S_{N,N}
T_{1,1}T_{1,2}\dots T_{1,N}
\vdots
T_{N,1}T_{N,2}\dots T_{N,N}

Output

Output the minimum number of operations required.

Sample Input 1

4
###.
..#.
..#.
..#.
...#
...#
###.
....

Sample Output 1

You can match S to T in two operations as shown below.

Sample Input 2

13
.#..###..##..
#.#.#..#.#.#.
#.#.###..#...
###.#..#.#.#.
#.#.###..##..
.............
..#...#....#.
.##..#.#..##.
#.#..#.#.#.#.
####.#.#.####
..#..#.#...#.
..#...#....#.
.............
.............
.#....#...#..
.#...#.#..#..
####.#.#.####
.#.#.###..#.#
.##....#..##.
.#....#...#..
.............
..##..###.#.#
.#.#.#..#.###
.#.#..###.#.#
.#.#.#..#.#.#
..##..###..#.

Sample Output 2

C - Cycle Graph?

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 300 点

問題文

N 頂点 M 辺の単純無向グラフが与えられます。頂点には 1,2,\dots,N の番号が、辺には 1,2,\dots,M の番号がつけられており、辺 i は頂点 A_i と頂点 B_i を結んでいます。

このグラフがサイクルグラフであるか判定してください。

単純無向グラフとは

単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。

サイクルグラフとは

頂点に 1, 2, \dots, N の番号が付けられた N 頂点のグラフがサイクルグラフであるとは、(1, 2, \dots, N) を並べ変えて得られる数列 (v_1, v_2, \dots, v_N) であって、以下の条件を満たすものが存在することをいいます。

i = 1, 2, \dots, N-1 に対して、頂点 v_i と v_{i+1} を結ぶ辺が存在する
頂点 v_N と v_1 を結ぶ辺が存在する
それら以外の辺は存在しない

制約

3\leq N \leq 2\times 10^5
0 \leq M \leq 2\times 10^5
1 \leq A_i, B_i \leq N
与えられるグラフは単純
入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 B_1
\vdots
A_M B_M

出力

与えられたグラフがサイクルグラフであるなら Yes、そうでないなら No と出力せよ。

入力例 1

出力例 1

Yes

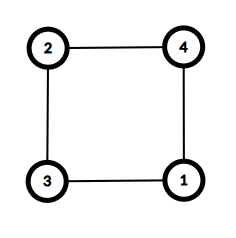
与えられたグラフは以下の通りであり、これはサイクルグラフです。

入力例 2

出力例 2

No

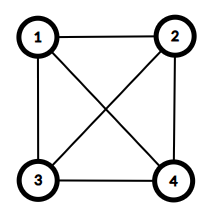
与えられたグラフは以下の通りであり、これはサイクルグラフではありません。

Score : 300 points

Problem Statement

You are given a simple undirected graph with N vertices and M edges. The vertices are numbered 1,2,\dots,N and the edges are numbered 1,2,\dots,M. Edge i connects vertices A_i and B_i.

Determine whether this graph is a cycle graph.

Definition of simple undirected graph

A simple undirected graph is a graph with undirected edges without self-loops or multi-edges.

Definition of cycle graph

An N-vertex graph with vertices labeled 1,2,\dots,N is a cycle graph when there exists a permutation (v_1,v_2,\dots,v_N) of (1,2,\dots,N) such that:

For each i = 1,2,\dots,N-1, there is an edge between vertices v_i and v_{i+1}.
There is an edge between vertices v_N and v_1.
No other edges exist.

Constraints

3 \le N \le 2\times 10^5
0 \le M \le 2\times 10^5
1 \le A_i, B_i \le N
The given graph is simple.
All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 B_1
\vdots
A_M B_M

Output

Output Yes if the given graph is a cycle graph; otherwise, print No.

Sample Input 1

Sample Output 1

Yes

The given graph is as follows, and this is a cycle graph.

Sample Input 2

Sample Output 2

No

The given graph is as follows, and this is not a cycle graph.

D - Goin' to the Zoo

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 400 点

問題文

AtCoder 国には動物園が N 園あり、1 から N の番号がついています。動物園 i の入園料は C_i 円です。

鈴木さんは M 種類の動物、動物 1,\ldots,M が好きです。
動物 i は K_i 園の動物園 A_{i,1},\dots, A_{i,K_i} で見ることができます。

M 種類の動物全てを 2 度以上ずつ見るために必要な入園料の合計の最小値を求めてください。
なお、同じ動物園を複数回訪れた場合、その動物園の動物は訪れた回数だけ見たとみなします。

制約

1\leq N \leq 10
1\leq M \leq 100
0\leq C_i \leq 10^9
1\leq K_i \leq N
1 \leq A_{i,j} \leq N
j \neq j' \Longrightarrow A_{i,j}\neq A_{i,j'}
入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
C_1 \dots C_N
K_1 A_{1,1} \dots A_{1,K_1}
\vdots
K_M A_{M,1} \dots A_{M,K_M}

出力

答えを出力せよ。

入力例 1

4 3
1000 300 700 200
3 1 3 4
3 1 2 4
2 1 3

出力例 1

以下のようにすることで、1800 円で動物 1,2,3 を 2 度以上ずつ見ることができます。

動物園 3 に行く。入園料 700 円を払い、動物 1,3 を見る。
動物園 3 に行く。入園料 700 円を払い、動物 1,3 を見る。
動物園 4 に行く。入園料 200 円を払い、動物 1,2 を見る。
動物園 4 に行く。入園料 200 円を払い、動物 1,2 を見る。

入力例 2

7 6
500 500 500 500 500 500 1000
3 1 2 7
3 2 3 7
3 3 4 7
3 4 5 7
3 5 6 7
3 6 1 7

出力例 2

動物園 7 に 2 度行くことで、合計 2000 円で動物 1,2,3,4,5,6 を 2 度ずつ見ることができます。

Score : 400 points

Problem Statement

In the country of AtCoder there are N zoos, numbered 1 to N. The admission fee for zoo i is C_i yen.

Mr. Suzuki likes M kinds of animals, animals 1,\dots,M.
Animal i can be seen at K_i zoos, namely zoos A_{i,1},\dots,A_{i,K_i}.

Find the minimum total admission fee required to see all M kinds of animals at least twice each.
If you visit the same zoo multiple times, the animals there are considered seen once per every visit.

Constraints

1 \le N \le 10
1 \le M \le 100
0 \le C_i \le 10^9
1 \le K_i \le N
1 \le A_{i,j} \le N
j \neq j' \Longrightarrow A_{i,j} \neq A_{i,j'}
All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
C_1 \dots C_N
K_1 A_{1,1} \dots A_{1,K_1}
\vdots
K_M A_{M,1} \dots A_{M,K_M}

Output

Output the minimum total admission fee.

Sample Input 1

4 3
1000 300 700 200
3 1 3 4
3 1 2 4
2 1 3

Sample Output 1

For example, the following schedule achieves seeing animals 1,2,3 at least twice each for a total of 1800 yen:

Go to zoo 3. Pay 700 yen and see animals 1 and 3.
Go to zoo 3. Pay 700 yen and see animals 1 and 3.
Go to zoo 4. Pay 200 yen and see animals 1 and 2.
Go to zoo 4. Pay 200 yen and see animals 1 and 2.

Sample Input 2

7 6
500 500 500 500 500 500 1000
3 1 2 7
3 2 3 7
3 3 4 7
3 4 5 7
3 5 6 7
3 6 1 7

Sample Output 2

By visiting zoo 7 twice, you can see animals 1,2,3,4,5,6 twice each for a total of 2000 yen.

E - Bowls and Beans

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 475 点

問題文

N 個の大きな茶碗が横一列に並んでおり、左から茶碗 0,1,\dots,N-1 と番号付けされています。
茶碗 i ( 1 \le i \le N-1 ) には整数 C_i が書かれており、初めに中には A_i 個の豆が入っています。
茶碗 0 に整数は書かれておらず、初めは豆も入っていません。

以下の操作を繰り返すことを考えます。

ひとつの茶碗 i ( 1 \le i \le N-1 ) を選び、そこから 1 個以上の豆を取り出す。
取り出した豆を、茶碗 i-C_i,i-C_i+1,\dots,i-1 に自由に振り分けて入れる。
- 厳密には、豆を k 個取り出した際、茶碗 i-C_i,i-C_i+1,\dots,i-1 に合計 k 個の豆を入れる。このとき、どの茶碗にいくつ豆を入れるかの振り分け方を任意に指定して入れる。

全ての豆が茶碗 0 にある状態にするために必要な最小の操作回数を求めてください。

制約

入力は全て整数
2 \le N \le 2000
1 \le C_i \le i
0 \le A_i \le 1
\displaystyle \sum_{i=1}^{N-1} A_i > 0

入力

入力は以下の形式で標準入力から与えられる。

N
C_1 C_2 \dots C_{N-1}
A_1 A_2 \dots A_{N-1}

出力

答えを整数として出力せよ。

入力例 1

5
1 1 2 1
1 0 0 1

出力例 1

例えば以下の 3 回の操作で全ての豆が茶碗 0 にある状態にすることができ、これが最小です。

茶碗 4 を選択する。この茶碗の中には豆が 1 つ入っている。
- 豆のうち 1 つを茶碗 3 に入れる。
茶碗 3 を選択する。この茶碗の中には豆が 1 つ入っている。
- 豆のうち 1 つを茶碗 1 に入れる。
茶碗 1 を選択する。この茶碗の中には豆が 2 つ入っている。
- 豆のうち 2 つを茶碗 0 に入れる。

入力例 2

6
1 2 1 3 1
1 1 0 1 1

出力例 2

例えば以下の 4 回の操作で全ての豆が茶碗 0 にある状態にすることができ、これが最小です。

茶碗 5 を選択する。この茶碗の中には豆が 1 つ入っている。
- 豆のうち 1 つを茶碗 4 に入れる。
茶碗 4 を選択する。この茶碗の中には豆が 2 つ入っている。
- 豆のうち 1 つを茶碗 1 に入れる。
- 豆のうち 1 つを茶碗 2 に入れる。
茶碗 1 を選択する。この茶碗の中には豆が 2 つ入っている。
- 豆のうち 2 つを茶碗 0 に入れる。
茶碗 2 を選択する。この茶碗の中には豆が 2 つ入っている。
- 豆のうち 2 つを茶碗 0 に入れる。

入力例 3

16
1 1 1 2 5 1 1 3 4 1 4 3 1 1 2
1 0 0 0 1 0 0 1 1 0 0 0 0 0 1

出力例 3

Score : 475 points

Problem Statement

There are N large bowls arranged in a row, numbered 0,1,\dots,N-1 from the left.
For each bowl i ( 1\le i\le N-1 ), an integer C_i is written on it, and initially it contains A_i beans.
Bowl 0 has no integer written on it and initially contains no beans.

Consider repeating the following operation any number of times:

Choose one bowl i (1\le i\le N-1) and take out one or more beans from it.
Distribute the taken beans freely among bowls i-C_i,i-C_i+1,\dots,i-1.
- Formally, when you take out k beans, you must put a total of k beans into bowls i-C_i,i-C_i+1,\dots,i-1, and you may choose how many beans go into each bowl.

Find the minimum number of operations required to put all the beans into bowl 0.

Constraints

All input values are integers.
2 \le N \le 2000
1 \le C_i \le i
0 \le A_i \le 1
\displaystyle \sum_{i=1}^{N-1} A_i > 0

Input

The input is given from Standard Input in the following format:

N
C_1 C_2 \dots C_{N-1}
A_1 A_2 \dots A_{N-1}

Output

Output the answer as an integer.

Sample Input 1

5
1 1 2 1
1 0 0 1

Sample Output 1

For example, the following three operations put all the beans into bowl 0, and this is the minimum:

Choose bowl 4. It has 1 bean.
- Put 1 bean into bowl 3.
Choose bowl 3. It has 1 bean.
- Put 1 bean into bowl 1.
Choose bowl 1. It has 2 beans.
- Put 2 beans into bowl 0.

Sample Input 2

6
1 2 1 3 1
1 1 0 1 1

Sample Output 2

For example, the following four operations put all the beans into bowl 0, and this is the minimum:

Choose bowl 5. It has 1 bean.
- Put 1 bean into bowl 4.
Choose bowl 4. It has 2 beans.
- Put 1 bean into bowl 1.
- Put 1 bean into bowl 2.
Choose bowl 1. It has 2 beans.
- Put 2 beans into bowl 0.
Choose bowl 2. It has 2 beans.
- Put 2 beans into bowl 0.

Sample Input 3

16
1 1 1 2 5 1 1 3 4 1 4 3 1 1 2
1 0 0 0 1 0 0 1 1 0 0 0 0 0 1

Sample Output 3

F - Lost and Pound

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 550 点

問題文

N 個の押しボタンがあります。このうち 1 個が当たりで、残りの N-1 個はハズレです。

青木君はどのボタンが当たりであるか知っており、高橋君は知りません。また高橋君には N 個のボタンの区別はつきません。

このボタンを使って青木君と高橋君がゲームを行います。ゲームは以下の一連の流れの T 回の繰り返しからなります。

青木君が N 個のボタンをランダムな順序に並べる
高橋君が「ボタンを 1 つ選び、そのボタンを押す」という操作を M 回行う。同じボタンを複数回選んでもよい
ゲーム開始時からこれまでに当たりのボタンが何回押されたかを青木君が高橋君に教える

T 回の繰り返しで、当たりのボタンを合計 K 回以上押すことができたとき、かつ、そのときに限り高橋君の勝ちです。

勝つ確率が最大になるように高橋君が行動したときの、高橋君の勝率を求めてください。

制約

1 \leq N \leq 2\times 10^5
1 \leq T \leq 30
1 \leq M \leq 30
1 \leq K \leq 30
入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N T M K

出力

答えを出力せよ。真の解との絶対誤差または相対誤差が 10^{-6} 以下のとき正解と判定される。

入力例 1

3 2 2 3

出力例 1

0.222222222222222

ゲームは例えば次のように進行します。（最適な行動とは限りません）

1回目の繰り返し
- 青木君がボタンをランダムに並び替え、当たりのボタンが 1 番目、ハズレのボタンが 2,3 番目となる
- 高橋君が 1 番目のボタンを押す
- 高橋君が 2 番目のボタンを押す
- 当たりのボタンが 1 度押されたことを青木君が高橋君に伝える
2回目の繰り返し
- 青木君がボタンをランダムに並び替え、当たりのボタンが 3 番目、ハズレのボタンが 1,2 番目となる
- 高橋君が 3 番目のボタンを押す
- 高橋君が 3 番目のボタンを押す
- 当たりのボタンが 3 度押されたことを青木君が高橋君に伝える
当たりのボタンを 3 回以上押したため、高橋君の勝ちです

なお、このケースの真の解は \frac{2}{9} であるため、0.222222 や 0.222223141592 などの出力でも正解と判定されます。

入力例 2

10 1 10 1

出力例 2

1.000000000000000

入力例 3

100 10 10 2

出力例 3

0.401263060761621

Score : 550 points

Problem Statement

There are N push buttons. One of them is the winning button, and the other N-1 are losing buttons.

Aoki knows which button is winning, but Takahashi does not. Also, Takahashi cannot distinguish the N buttons.

They play a game using these buttons. The game consists of repeating the following sequence T times:

Aoki arranges the N buttons in a random order.
Takahashi performs the operation “choose a button and press it” M times. He may choose the same button multiple times.
Aoki tells Takahashi the number of times the winning button has been pressed so far since the start of the game.

Takahashi wins if and only if the winning button has been pressed a total of at least K times throughout the T repetitions.

Find Takahashi’s probability of winning when he plays to maximize his win probability.

Constraints

1 \le N \le 2\times 10^5
1 \le T \le 30
1 \le M \le 30
1 \le K \le 30
All input values are integers.

Input

The input is given from Standard Input in the following format:

N T M K

Output

Output the answer. Your output is considered correct if its absolute or relative error from the true answer is at most 10^{-6}.

Sample Input 1

3 2 2 3

Sample Output 1

0.222222222222222

The game can proceed as follows (not necessarily optimally):

1st repetition
- Aoki randomly arranges the buttons so that the winning button is at position 1, and the losing buttons are at positions 2 and 3.
- Takahashi presses button 1.
- Takahashi presses button 2.
- Aoki tells him the winning button has been pressed 1 time.
2nd repetition
- Aoki randomly arranges the buttons so that the winning button is at position 3, and the losing buttons are at positions 1 and 2.
- Takahashi presses button 3.
- Takahashi presses button 3.
- Aoki tells him the winning button has been pressed 3 times.
Since the winning button has been pressed not less than 3 times, Takahashi wins.

The true answer in this case is \tfrac{2}{9}, so outputs like 0.222222 or 0.222223141592 are also accepted.

Sample Input 2

10 1 10 1

Sample Output 2

1.000000000000000

Sample Input 3

100 10 10 2

Sample Output 3

0.401263060761621

G - Specified Range Sums

実行時間制限: 2 sec / メモリ制限: 1024 MiB

配点 : 600 点

問題文

整数 N と長さ M の整数列 L=(L_1,L_2,\dots,L_M),R=(R_1,R_2,\dots,R_M),S=(S_1,S_2,\dots,S_M) が与えられるので、次の問題を解いてください。

以下の条件を満たす長さ N の 正整数列 A が存在するか判定し、存在する場合は A の総和としてありうる最小値を求めてください。

全ての i ( 1 \le i \le M ) について、 \displaystyle \sum_{j=L_i}^{R_i} A_j = S_i を満たす。

制約

入力は全て整数
1 \le N,M \le 4000
1 \le L_i \le R_i \le N
1 \le S_i \le 10^9

入力

入力は以下の形式で標準入力から与えられる。

N M
L_1 R_1 S_1
L_2 R_2 S_2
\vdots
L_M R_M S_M

出力

問題文中の条件を満たす長さ N の正整数列 A が存在しない場合、 -1 と出力せよ。
そうでない場合、 A の総和としてありうる最小値を整数として出力せよ。

入力例 1

出力例 1

例えば、 A=(1,3,2,1,5) は問題文中の条件を満たします。
このとき A の総和は 12 で、これがありうる最小値です。

入力例 2

1 2
1 1 1
1 1 2

出力例 2

-1

問題文中の条件を満たす A が存在しないこともあります。

入力例 3

出力例 3

Score : 600 points

Problem Statement

You are given an integer N and length-M integer sequences L=(L_1,L_2,\dots,L_M), R=(R_1,R_2,\dots,R_M), and S=(S_1,S_2,\dots,S_M).

Determine whether there exists a length-N positive integer sequence A satisfying the following condition. If such a sequence exists, find the minimum possible sum of A.

\displaystyle \sum_{j=L_i}^{R_i} A_j = S_i for all i ( 1 \le i \le M ).

Constraints

All input values are integers.
1 \le N,M \le 4000
1 \le L_i \le R_i \le N
1 \le S_i \le 10^9

Input

The input is given from Standard Input in the following format:

N M
L_1 R_1 S_1
L_2 R_2 S_2
\vdots
L_M R_M S_M

Output

If there does not exist a length-N positive integer sequence A satisfying the condition, print -1.
Otherwise, print the minimum possible sum of A as an integer.

Sample Input 1

Sample Output 1

For example, A=(1,3,2,1,5) satisfies the condition.
Its sum is 12, which is the minimum possible.

Sample Input 2

1 2
1 1 1
1 1 2

Sample Output 2

-1

Sometimes no such A exists.

Sample Input 3