Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
以下の条件を全て満たす長さ N の文字列を求めてください。
- 各文字は
-または=である - 回文である
- 文字列中に
=は 1 個または 2 個含まれる。 2 個含まれる場合、それらの=は隣接している
なお、そのような文字列はちょうど 1 つ存在します。
制約
- 1 \leq N \leq 100
- N は整数である
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを出力せよ。
入力例 1
4
出力例 1
-==-
入力例 2
7
出力例 2
---=---
Score : 100 points
Problem Statement
Find a length-N string that satisfies all of the following conditions:
- Each character is
-or=. - It is a palindrome.
- It contains exactly one or exactly two
=s. If it contains two=s, they are adjacent.
Such a string is unique.
Constraints
- 1 \leq N \leq 100
- N is an integer.
Input
The input is given from Standard Input in the following format:
N
Output
Print the answer.
Sample Input 1
4
Sample Output 1
-==-
Sample Input 2
7
Sample Output 2
---=---
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 250 点
問題文
7 枚のカードがあります。i 番目 (i=1,\ldots,7) のカードには整数 A_i が書かれています。
これらのカードから 5 枚を選び、フルハウスとできるか判定してください。
ただし、 5 枚組のカードは以下の条件を満たすとき、またそのときに限って、フルハウスであると呼ばれます。
- 異なる整数 x,y について、 x が書かれたカード 3 枚と y が書かれたカード 2 枚からなる。
制約
- A_i は 1 以上 13 以下の整数
入力
入力は以下の形式で標準入力から与えられる。
A_1 A_2 A_3 A_4 A_5 A_6 A_7
出力
5 枚カードを選んでフルハウスとできるなら Yes 、そうでないなら No と出力せよ。
入力例 1
1 4 1 4 2 1 3
出力例 1
Yes
例えば、 (1,1,1,4,4) とカードを選択することでフルハウスとできます。
入力例 2
11 12 13 10 13 12 11
出力例 2
No
7 枚のカードからどのように 5 枚を選んでもフルハウスとはできません。
入力例 3
7 7 7 7 7 7 7
出力例 3
No
同じカード 5 枚組はフルハウスではないことに注意してください。
入力例 4
13 13 1 1 7 4 13
出力例 4
Yes
Score : 250 points
Problem Statement
We have seven cards. The i-th card (i=1,\ldots,7) has an integer A_i written on it.
Determine whether it is possible to choose five of them so that the chosen cards form a full house.
A set of five cards is called a full house if and only if the following conditions are satisfied:
- For different integers x and y, there are three cards with x and two cards with y.
Constraints
- A_i is an integer between 1 and 13, inclusive.
Input
The input is given from Standard Input in the following format:
A_1 A_2 A_3 A_4 A_5 A_6 A_7
Output
If a full house can be formed by choosing five cards, print Yes; otherwise, print No.
Sample Input 1
1 4 1 4 2 1 3
Sample Output 1
Yes
For example, by choosing the cards (1,1,1,4,4), we can form a full house.
Sample Input 2
11 12 13 10 13 12 11
Sample Output 2
No
No five cards chosen from the seven cards form a full house.
Sample Input 3
7 7 7 7 7 7 7
Sample Output 3
No
Note that five identical cards do not form a full house.
Sample Input 4
13 13 1 1 7 4 13
Sample Output 4
Yes
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
1 から N の番号がついた N 人の人がいます。人 i は数 A_i を持っています。
「自分と同じ数を持っている人が自分以外の N-1 人の中に存在しない」という条件を満たす人のうち、持っている数が最大である人の番号を求めてください。
条件を満たす人が存在しない場合、代わりにそのことを報告してください。
制約
- 1 \leq N \leq 3\times 10^5
- 1 \leq A_i \leq 10^9
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
「自分と同じ数を持っている人が自分以外の N-1 人の中に存在しない」という条件を満たす人が存在しない場合、-1 と出力せよ。
条件を満たす人が存在する場合、そのうち、持っている数が最大である人の番号を出力せよ。
入力例 1
9 2 9 9 7 9 2 4 5 8
出力例 1
9
「自分と同じ数を持っている人が自分以外の N-1 人の中に存在しない」という条件を満たすのは人 4,7,8,9 の 4 人です。
これらの人が持っている数はそれぞれ 7,4,5,8 であり、最大の数を持っているのは人 9 です。
よって答えは 9 となります。
入力例 2
4 1000000000 1000000000 998244353 998244353
出力例 2
-1
条件を満たす人が存在しない場合、-1 を出力してください。
Score : 300 points
Problem Statement
There are N people, labeled 1 to N. Person i has an integer A_i.
Among the people who satisfy the condition "None of the other N-1 people has the same integer as themselves," find the one with the greatest integer, and print that person's label.
If no person satisfies the condition, report that fact instead.
Constraints
- 1 \leq N \leq 3\times 10^5
- 1 \leq A_i \leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
If no person satisfies the condition "None of the other N-1 people has the same integer as themselves," print -1.
Otherwise, among those who satisfy it, print the label of the person whose integer is the largest.
Sample Input 1
9 2 9 9 7 9 2 4 5 8
Sample Output 1
9
Those who satisfy the condition are the persons labeled 4, 7, 8, and 9.
Their integers are 7, 4, 5, and 8, respectively, and the person with the largest integer is the person labeled 9.
Thus, the answer is 9.
Sample Input 2
4 1000000000 1000000000 998244353 998244353
Sample Output 2
-1
If no person satisfies the condition, print -1.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
無限に広い 2 次元グリッドがあり、このグリッドの座標 (0,0) に焚き火があります。
時刻 t=0 では、マス (0,0) にのみ煙が存在します。
N, W, S, E からなる長さ N の文字列 S が与えられ、時刻 t=1,2,\dots,N では次の現象が順番に発生します。
- 風が吹き、現時点で存在する全ての煙が以下の通りに移動する。
- S の t 文字目が
Nであるとき、マス (r,c) にある煙がマス (r-1,c) に移動する。 - S の t 文字目が
Wであるとき、マス (r,c) にある煙がマス (r,c-1) に移動する。 - S の t 文字目が
Sであるとき、マス (r,c) にある煙がマス (r+1,c) に移動する。 - S の t 文字目が
Eであるとき、マス (r,c) にある煙がマス (r,c+1) に移動する。
- S の t 文字目が
- マス (0,0) に煙が存在しない場合、新たな煙がマス (0,0) に生成される。
高橋君はマス (R,C) に立っています。
整数 1 \le t \le N について、時刻 t+0.5 においてマス (R,C) に煙が存在するか判定し、出力欄の形式に従って出力してください。
制約
- N は 1 以上 200000 以下の整数
- S は
N,W,S,Eからなる長さ N の文字列 - R,C は -N 以上 N 以下の整数
- (R,C) \neq (0,0)
入力
入力は以下の形式で標準入力から与えられる。
N R C S
出力
答えを N 文字の 0, 1 からなる文字列として出力せよ。
出力する文字列のうち t 文字目 (1 \le t \le N) は次の通りにせよ。
- 時刻 t+0.5 においてマス (R,C) に煙が存在するなら
1 - 時刻 t+0.5 においてマス (R,C) に煙が存在しないなら
0
入力例 1
6 -2 1 NNEEWS
出力例 1
001010
時刻 1.5,2.5,4.5,6.5 ではマス (-2,1) には煙が存在せず、時刻 3.5,5.5 ではマス (-2,1) に煙が存在します。
よって、 001010 と出力します。
図では焚き火のあるマス (0,0) を基準として、マス (r,c) を
- r < 0 なら -r マス上に
- r \ge 0 なら r マス下に
- c < 0 なら -c マス左に
- c \ge 0 なら c マス右に
描画します。
時刻 0.5 でのグリッドの状態は次の通りです。
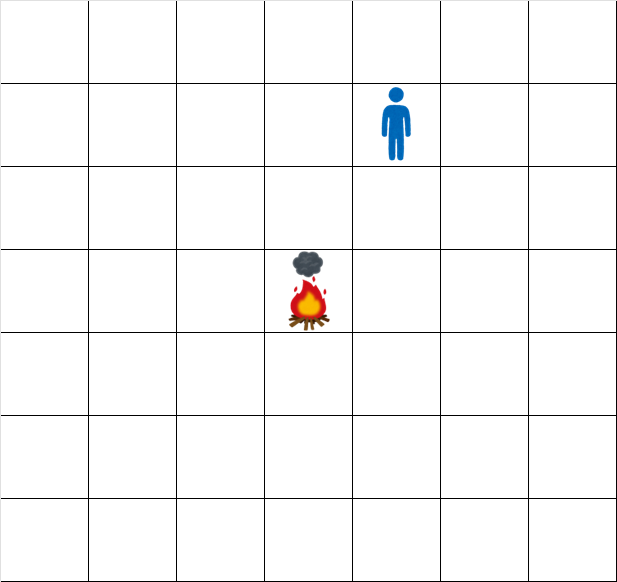
時刻 1.5 でのグリッドの状態は次の通りです。
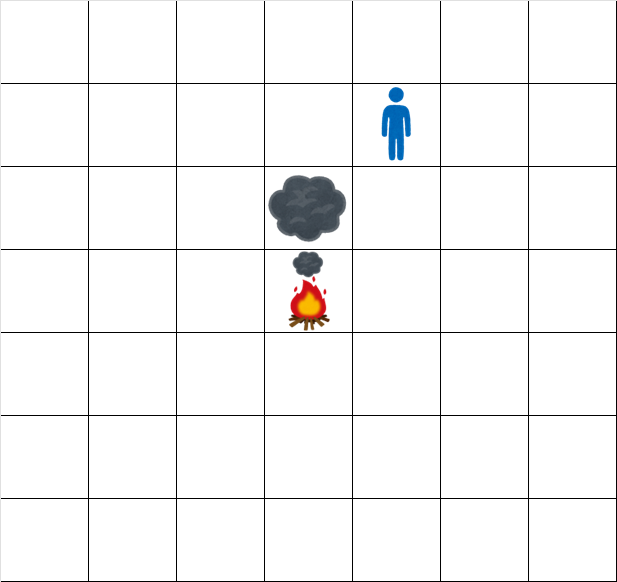
時刻 2.5 でのグリッドの状態は次の通りです。
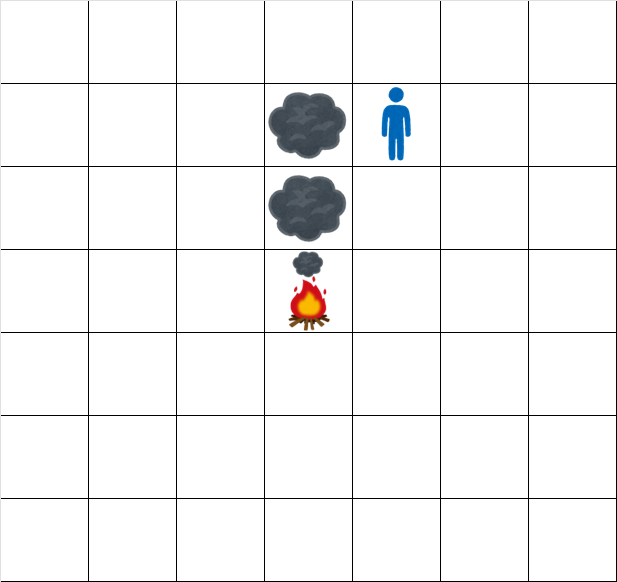
時刻 3.5 でのグリッドの状態は次の通りです。
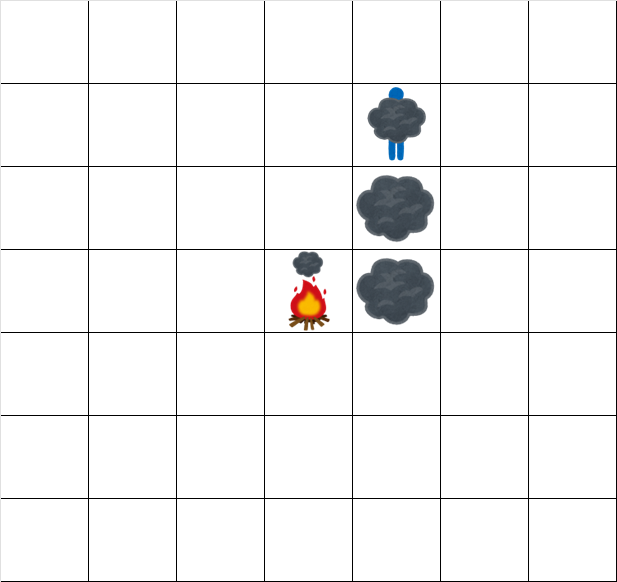
時刻 4.5 でのグリッドの状態は次の通りです。
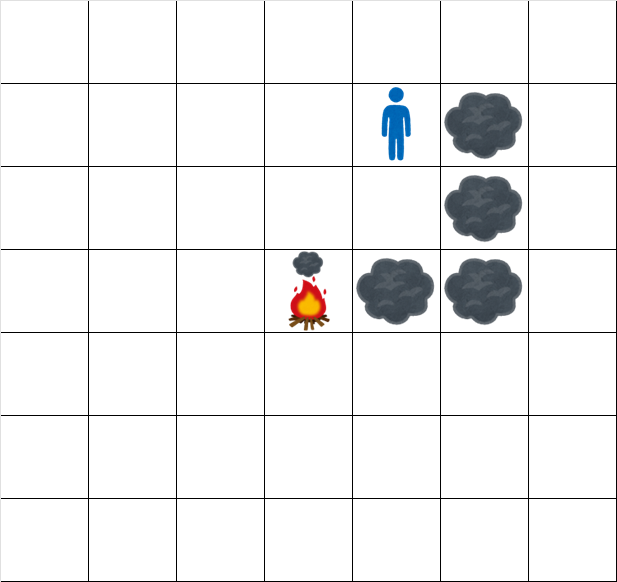
時刻 5.5 でのグリッドの状態は次の通りです。
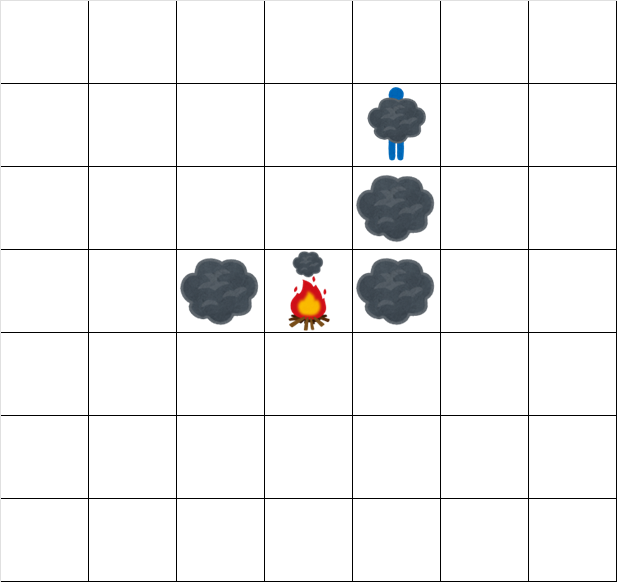
時刻 6.5 でのグリッドの状態は次の通りです。
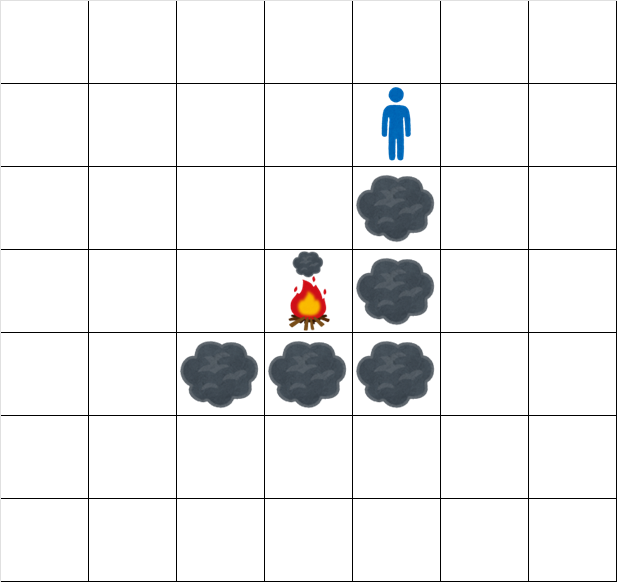
入力例 2
10 1 2 NEESESWEES
出力例 2
0001101011
入力例 3
20 -1 -2 WWNNWSWEWNSWWENSNWWN
出力例 3
00100111111000101111
Score : 425 points
Problem Statement
There is an infinitely large two-dimensional grid, with a campfire at coordinate (0,0).
At time t=0, smoke exists only at cell (0,0).
You are given a length-N string S consisting of N, W, S, E. At times t=1,2,\dots,N, the following happen in order:
- Wind blows, and all the smoke present at that time moves as follows:
- If the t-th character of S is
N, smoke in cell (r,c) moves to cell (r-1,c). - If it is
W, smoke in cell (r,c) moves to cell (r,c-1). - If it is
S, smoke in cell (r,c) moves to cell (r+1,c). - If it is
E, smoke in cell (r,c) moves to cell (r,c+1).
- If the t-th character of S is
- If there is no smoke in cell (0,0), new smoke is generated at cell (0,0).
Takahashi is standing at cell (R,C).
For each integer 1 \le t \le N, determine if smoke exists at cell (R,C) at time t+0.5, and print the response according to the required format.
Constraints
- N is an integer between 1 and 200000, inclusive.
- S is a length N string consisting of
N,W,S,E. - R and C are integers between -N and N, inclusive.
- (R,C) \neq (0,0)
Input
The input is given from Standard Input in the following format:
N R C S
Output
Print an N-character string consisting of 0 and 1.
The t-th character (1 \le t \le N) should be:
1if smoke exists at cell (R,C) at time t+0.5, and0otherwise.
Sample Input 1
6 -2 1 NNEEWS
Sample Output 1
001010
At times 1.5,2.5,4.5,6.5, there is no smoke at cell (-2,1). At times 3.5,5.5, there is smoke at cell (-2,1).
Hence, output 001010.
In the figures below, taking cell (0,0) with the campfire as a reference, cell (r,c) is drawn:
- -r cells up if r < 0,
- r cells down if r \ge 0,
- -c cells left if c < 0,
- c cells right if c \ge 0.
The grid at time 0.5 looks like:

The grid at time 1.5 looks like:

The grid at time 2.5 looks like:

The grid at time 3.5 looks like:

The grid at time 4.5 looks like:

The grid at time 5.5 looks like:

The grid at time 6.5 looks like:

Sample Input 2
10 1 2 NEESESWEES
Sample Output 2
0001101011
Sample Input 3
20 -1 -2 WWNNWSWEWNSWWENSNWWN
Sample Output 3
00100111111000101111
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
この問題は インタラクティブな問題 (あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題)です。
1 から N の番号がついた N 頂点からなる木 G が与えられます。i 番目の辺は頂点 U_i と頂点 V_i を結んでいます。
この木 G を使って、あなたと高橋君がゲームをします。まず、あなたは先手後手を決めます。その後、先手から順に交互に以下の操作を行います。
- 1 \leq i < j \leq N を満たす整数の組 (i,j) であって、以下の条件をともに満たすものを選び、頂点 i と頂点 j を結ぶ辺を G に追加する。
- G は頂点 i と頂点 j を結ぶ辺を持たない
- 頂点 i と頂点 j を結ぶ辺を G に追加しても、奇閉路ができない
操作を行えなくなった方が負けであり、負けでない方が勝ちです。実際に高橋君とゲームをして勝ってください。
奇閉路とは?
G の頂点の列 (v_0,v_1,\ldots,v_k) が以下の条件を全て満たすとき、かつ、そのときに限りこの列を G の奇閉路といいます。
- k は奇数である。
- v_0=v_k である。
- 全ての 1\leq i \leq k に対して、v_{i-1} と v_{i} を結ぶ辺が存在する。
制約
- 2 \leq N \leq 100
- 1 \leq U_i < V_i \leq N
- 与えられるグラフは木である
- 入力は全て整数である
入出力
この問題はインタラクティブな問題(あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題)です。
最初に、N および G の情報を標準入力から受け取ってください。以下の形式で与えられます。
N
U_1 V_1
U_2 V_2
\vdots
U_{N-1} V_{N-1}
次に、あなたが先手と後手のどちらを選ぶか決めてください。先手を選ぶ場合 First、後手を選ぶ場合 Second と標準出力に出力してください。
その後ゲームが始まります。
あなたの手番では、操作のために選んだ整数の組 (i,j) を、i,j の順に空白区切りで標準出力に出力してください。
i j
高橋君の手番では、2 つの整数 i,j が順に空白区切りで標準入力に与えられます。
i j
(i,j)=(-1,-1) のとき、あなたがゲームに勝利しゲームが終了したことを意味します。この場合、直ちにプログラムを終了してください。
それ以外のとき、(i,j) は高橋君が操作のために選んだ整数の組を表します。
注意点
- 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
- 対話の途中で誤った出力形式による出力を行った、あるいはプログラムが途中で終了した場合のジャッジ結果は不定です。
- ゲームが終了したらただちにプログラムを終了してください。そうしない場合、ジャッジ結果は不定です。
入出力例
| 入力 | 出力 | 説明 |
|---|---|---|
41 22 33 4 | まず整数 N および G の情報が与えられます。 | |
First | あなたは先手を選びました。 | |
1 4 | あなたは (1,4) に対して操作を行いました。 | |
-1 -1 | 高橋君が操作を行えなくなったためゲームを終了します。ジャッジ結果は になります。 |
Score : 425 points
Problem Statement
This problem is an interactive problem (in which your program and the judge system communicate via input and output).
You are given a tree G with N vertices numbered 1 to N. The i-th edge connects vertices U_i and V_i.
You will play a game with Takahashi using this tree G. First, you decide who is first and who is second. Then, starting from the first player, take turns performing the following operation:
- Choose a pair of integers (i,j) with 1 \leq i < j \leq N that satisfies both of the following conditions, then add an edge connecting vertices i and j to G.
- G does not already have an edge connecting vertices i and j.
- Adding an edge connecting vertices i and j does not create an odd cycle.
A player who cannot perform this operation loses, and the other player wins. Play this game against Takahashi and win.
What is an odd cycle?
A sequence of vertices (v_0,v_1,\ldots,v_k) of G is called an odd cycle if and only if all of the following conditions are satisfied:
- k is odd.
- v_0=v_k.
- For every 1\leq i \leq k, there is an edge connecting v_{i-1} and v_{i}.
Constraints
- 2 \leq N \leq 100
- 1 \leq U_i < V_i \leq N
- The given graph is a tree.
- All input values are integers.
Interaction
This is an interactive problem (in which your program and the judge system communicate via input and output).
First, read N and the edges of G from Standard Input, given in the following format:
N
U_1 V_1
U_2 V_2
\vdots
U_{N-1} V_{N-1}
Then, decide whether you go first or second. If you choose first, print First; if second, print Second.
Then, the game begins.
On your turn, output the chosen pair (i,j) by printing two integers i and j in this order, separated by a space:
i j
On Takahashi's turn, two integers i,j will be given in order, separated by a space, via Standard Input:
i j
If (i,j)=(-1,-1), it means he can no longer make a move and you win. Immediately terminate your program in this case.
Otherwise, (i,j) is the pair of integers he has chosen.
Notes
- After each output, be sure to print a newline and flush Standard Output. Otherwise, you may get TLE.
- If you produce output in an incorrect format or your program ends prematurely, the judge result is indeterminate.
- Once the game finishes, terminate your program immediately. Otherwise, the judge result is indeterminate.
Sample Interaction
| Input | Output | Explanation |
|---|---|---|
41 22 33 4 |
First, you receive N and the edges of G. | |
First |
You choose to go first. | |
1 4 |
You add an edge between vertices 1 and 4. | |
-1 -1 |
Takahashi can no longer move, so you win. The judge result will be . |
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
S を接頭辞に持つ最短の回文を 1 つ求めてください。
制約
- S は英大文字からなる長さ 1 以上 500000 以下の文字列
入力
入力は以下の形式で標準入力から与えられる。
S
出力
答えを出力せよ。
解が複数存在する場合、どれを出力しても正解とみなされる。
入力例 1
ABC
出力例 1
ABCBA
ABCBA は S= ABC を接頭辞に持つ最短の回文です。
入力例 2
Z
出力例 2
Z
Z は S= Z を接頭辞に持つ最短の回文です。
入力例 3
TREE
出力例 3
TREERT
TREERT は S= TREE を接頭辞に持つ最短の回文です。
Score : 500 points
Problem Statement
Find one shortest palindrome that has S as its prefix.
Constraints
- S is a string of length between 1 and 500000, inclusive, consisting of uppercase English letters.
Input
The input is given from Standard Input in the following format:
S
Output
Print the answer.
If multiple solutions exist, any of them is accepted.
Sample Input 1
ABC
Sample Output 1
ABCBA
ABCBA is a shortest palindrome that has S= ABC as its prefix.
Sample Input 2
Z
Sample Output 2
Z
Z is a shortest palindrome that has S= Z as its prefix.
Sample Input 3
TREE
Sample Output 3
TREERT
TREERT is a shortest palindrome that has S= TREE as its prefix.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
頂点に 1 から N の番号が、辺に 1 から M の番号がついた N 頂点 M 辺からなる単純無向グラフが与えられます。 i 番目の辺は頂点 U_i と頂点 V_i を結んでいます。最初、 G は奇閉路を持ちません。
このグラフ G を使って、青木君と高橋君がゲームをします。先手の青木君から順に交互に以下の操作を行います。
- 1 \leq i < j \leq N を満たす整数の組 (i,j) であって、以下の条件をともに満たすものを選び、頂点 i と頂点 j を結ぶ辺を G に追加する。
- G は頂点 i と頂点 j を結ぶ辺を持たない
- 頂点 i と頂点 j を結ぶ辺を G に追加しても、奇閉路ができない
操作を行えなくなった方が負けであり、負けでない方が勝ちです。
両者が最適に行動したとき、どちらが勝つか判定してください。
奇閉路とは?
G の頂点の列 (v_0,v_1,\ldots,v_k) が以下の条件を全て満たすとき、かつ、そのときに限りこの列を G の奇閉路といいます。
- k は奇数である。
- v_0=v_k である。
- 全ての 1\leq i \leq k に対して、v_{i-1} と v_{i} を結ぶ辺が存在する。
制約
- 1 \leq N \leq 2\times 10^5
- 0 \leq M \leq 2\times 10^5
- 1 \leq U_i < V_i \leq N
- 与えられるグラフは奇閉路を持たない
- 与えられるグラフは多重辺を持たない
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 U_2 V_2 \vdots U_M V_M
出力
先手の青木君が勝つならば Aoki、後手の高橋君が勝つならば Takahashi と出力せよ。
入力例 1
4 3 1 2 2 3 3 4
出力例 1
Aoki
先手の青木君が (1,4) を選んで辺を追加すると、後手の高橋君は操作を行うことができません。よって青木君が勝ちます。
入力例 2
4 2 1 2 3 4
出力例 2
Takahashi
青木君がどのように操作を行っても、高橋君が勝ちます。
入力例 3
9 5 2 9 2 3 4 6 5 7 1 8
出力例 3
Aoki
Score : 600 points
Problem Statement
You are given a simple undirected graph with N vertices and M edges, with vertices labeled 1 to N and edges labeled 1 to M. The i-th edge connects vertices U_i and V_i. Initially, G does not contain an odd cycle.
Takahashi and Aoki will play a game using this graph G. With Aoki going first, they take turns performing the following operation:
- Choose a pair of integers (i,j) with 1 \leq i < j \leq N that satisfies both of the following conditions, then add an edge connecting vertices i and j to G.
- G does not already have an edge connecting vertices i and j.
- Adding an edge connecting vertices i and j does not create an odd cycle.
A player who cannot perform this operation loses, and the other player wins.
Determine who wins when both players play optimally.
What is an odd cycle?
A sequence of vertices (v_0,v_1,\ldots,v_k) of G is called an odd cycle if and only if all of the following conditions are satisfied:
- k is odd.
- v_0=v_k.
- For every 1\leq i \leq k, there is an edge connecting v_{i-1} and v_{i}.
Constraints
- 1 \leq N \leq 2\times 10^5
- 0 \leq M \leq 2\times 10^5
- 1 \leq U_i < V_i \leq N
- The given graph does not contain an odd cycle.
- The given graph does not contain multi-edges.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M U_1 V_1 U_2 V_2 \vdots U_M V_M
Output
If Aoki (the first player) wins, print Aoki; otherwise, if Takahashi (the second player) wins, print Takahashi.
Sample Input 1
4 3 1 2 2 3 3 4
Sample Output 1
Aoki
If Aoki (the first player) adds the edge (1,4), Takahashi (the second player) cannot move. Thus, Aoki wins.
Sample Input 2
4 2 1 2 3 4
Sample Output 2
Takahashi
No matter how Aoki plays, Takahashi wins.
Sample Input 3
9 5 2 9 2 3 4 6 5 7 1 8
Sample Output 3
Aoki