実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 100 点
問題文
ナオヒロ君はモンスターを飼っています。モンスターの現在の体力は H です。
また、ナオヒロ君は N 種類の傷薬を持っています。傷薬は効き目の弱い順に 1 から N までの番号がついています。
傷薬 n をモンスターに与えると、モンスターの体力が P_n 増加します。ここで、P_1 \lt P_2 \lt \dots \lt P_N が成り立ちます。
ナオヒロ君は傷薬を 1 つモンスターに与えることで、モンスターの体力を X 以上にしたいです。
目標を達成できる傷薬のうち最も効き目の弱いものの番号を出力してください。(制約下においてそのような傷薬が存在することが保証されています。)
制約
- 2 \leq N \leq 100
- 1 \leq H \lt X \leq 999
- 1 \leq P_1 \lt P_2 \lt \dots \lt P_N = 999
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N H X P_1 P_2 \dots P_N
出力
目標を達成できる傷薬のうち最も効き目の弱いものの番号を出力せよ。
入力例 1
3 100 200 50 200 999
出力例 1
2
それぞれの傷薬をモンスターに 1 つ与えたときのモンスターの体力の変化は以下の通りです。
- 傷薬 1 をモンスターに与えるとモンスターの体力は 100 + 50 = 150 になります。
- 傷薬 2 をモンスターに与えるとモンスターの体力は 100 + 200 = 300 になります。
- 傷薬 3 をモンスターに与えるとモンスターの体力は 100 + 999 = 1099 になります。
与えた後に体力が X = 200 以上になっている傷薬は、傷薬 2 と傷薬 3 です。このうち最も効き目の弱い傷薬である傷薬 2 が答えになります。
入力例 2
2 10 21 10 999
出力例 2
2
入力例 3
10 500 999 38 420 490 585 613 614 760 926 945 999
出力例 3
4
Score : 100 points
Problem Statement
Naohiro has a monster. The monster's current health is H.
He also has N kinds of potions, numbered from 1 to N in ascending order of effectiveness.
If you give the monster potion n, its health will increase by P_n. Here, P_1 \lt P_2 \lt \dots \lt P_N.
He wants to increase the monster's health to X or above by giving it one of the potions.
Print the number of the least effective potion that can achieve the purpose. (The constraints guarantee that such a potion exists.)
Constraints
- 2 \leq N \leq 100
- 1 \leq H \lt X \leq 999
- 1 \leq P_1 \lt P_2 \lt \dots \lt P_N = 999
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N H X P_1 P_2 \dots P_N
Output
Print the number of the least effective potion that can achieve the purpose.
Sample Input 1
3 100 200 50 200 999
Sample Output 1
2
Below is the change in the monster's health when one of the potions is given to the monster.
- If potion 1 is given, the monster's health becomes 100 + 50 = 150.
- If potion 2 is given, the monster's health becomes 100 + 200 = 300.
- If potion 3 is given, the monster's health becomes 100 + 999 = 1099.
The potions that increase the monster's health to at least X = 200 are potions 2 and 3. The answer is the least effective of them, which is potion 2.
Sample Input 2
2 10 21 10 999
Sample Output 2
2
Sample Input 3
10 500 999 38 420 490 585 613 614 760 926 945 999
Sample Output 3
4
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 200 点
問題文
ナオヒロ君は N+1 個の連続する整数を 1 個ずつ持っていましたが、そのうち 1 個をなくしてしまいました。
残っている N 個の整数が順不同で A_1,\ldots,A_N として与えられるので、なくした整数を求めてください。
なお、なくした整数が一意に定まるような入力のみが与えられます。
制約
- 2 \leq N \leq 100
- 1 \leq A_i \leq 1000
- 入力は全て整数である
- なくした整数は一意に定まる
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
答えを出力せよ。
入力例 1
3 2 3 5
出力例 1
4
ナオヒロ君は初め 2,3,4,5 の 4 個の整数を持っており、4 をなくし、2,3,5 が残っていました。
なくした整数である 4 を出力します。
入力例 2
8 3 1 4 5 9 2 6 8
出力例 2
7
入力例 3
16 152 153 154 147 148 149 158 159 160 155 156 157 144 145 146 150
出力例 3
151
Score : 200 points
Problem Statement
Naohiro had N+1 consecutive integers, one of each, but he lost one of them.
The remaining N integers are given in arbitrary order as A_1,\ldots,A_N. Find the lost integer.
The given input guarantees that the lost integer is uniquely determined.
Constraints
- 2 \leq N \leq 100
- 1 \leq A_i \leq 1000
- All input values are integers.
- The lost integer is uniquely determined.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
Print the answer.
Sample Input 1
3 2 3 5
Sample Output 1
4
Naohiro originally had four integers, 2,3,4,5, then lost 4, and now has 2,3,5.
Print the lost integer, 4.
Sample Input 2
8 3 1 4 5 9 2 6 8
Sample Output 2
7
Sample Input 3
16 152 153 154 147 148 149 158 159 160 155 156 157 144 145 146 150
Sample Output 3
151
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 300 点
問題文
ある地方に、1 から N の番号がついた N 個の街と、1 から M の番号がついた M 本の道路があります。
i 番目の道路は街 A_i と街 B_i を双方向に結び、長さは C_i です。
好きな街からスタートして同じ街を二度以上通らずに別の街へ移動するときの、通る道路の長さの和としてありえる最大値を求めてください。
制約
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1\leq A_i < B_i \leq N
- (A_i,B_i) は相異なる
- 1\leq C_i \leq 10^8
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 C_1 \vdots A_M B_M C_M
出力
答えを出力せよ。
入力例 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
出力例 1
1110
4\to 1\to 3\to 2 と移動すると、通る道路の長さの和は 1110 となります。
入力例 2
10 1 5 9 1
出力例 2
1
道路と繋がっていない街が存在するかもしれません。
入力例 3
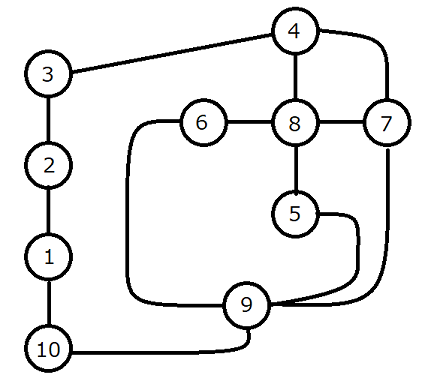
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
出力例 3
20
Score : 300 points
Problem Statement
A region has N towns numbered 1 to N, and M roads numbered 1 to M.
The i-th road connects town A_i and town B_i bidirectionally with length C_i.
Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.
Constraints
- 2 \leq N \leq 10
- 1 \leq M \leq \frac{N(N-1)}{2}
- 1 \leq A_i < B_i \leq N
- The pairs (A_i,B_i) are distinct.
- 1\leq C_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A_1 B_1 C_1 \vdots A_M B_M C_M
Output
Print the answer.
Sample Input 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
Sample Output 1
1110
If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.
Sample Input 2
10 1 5 9 1
Sample Output 2
1
There may be a town that is not connected to a road.
Sample Input 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
Sample Output 3
20

実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 400 点
問題文
高橋君と青木君が選挙で戦っています。
選挙区は N 個あります。i 番目の選挙区には X_i + Y_i 人の有権者がいて、そのうち X_i 人が高橋派、Y_i 人が青木派です。(X_i + Y_i はすべて奇数です)
それぞれの区では、多数派がその区の Z_i 議席を全て獲得します。そして、N 個の選挙区全体として過半数の議席を獲得した方が選挙に勝利します。(\displaystyle \sum_{i=1}^N Z_i は奇数です)
高橋君が選挙で勝利するには最低で何人を青木派から高橋派に鞍替えさせる必要がありますか?
制約
- 1 \leq N \leq 100
- 0 \leq X_i, Y_i \leq 10^9
- X_i + Y_i は奇数
- 1 \leq Z_i
- \displaystyle \sum_{i=1}^N Z_i \leq 10^5
- \displaystyle \sum_{i=1}^N Z_i は奇数
入力
入力は以下の形式で標準入力から与えられる。
N X_1 Y_1 Z_1 X_2 Y_2 Z_2 \vdots X_N Y_N Z_N
出力
答えを出力せよ。
入力例 1
1 3 8 1
出力例 1
3
選挙区が 1 個しかないので、1 番目の選挙区で議席を獲得した人が選挙に勝利します。
1 番目の選挙区の青木派 3 人を高橋派に鞍替えさせると、1 番目の選挙区にいる有権者のうち高橋派は 6 人、青木派は 5 人になり、高橋君は議席を獲得できます。
入力例 2
2 3 6 2 1 8 5
出力例 2
4
1 番目の選挙区の議席数よりも 2 番目の選挙区の議席数の方が多いため、高橋君が選挙に勝つには 2 番目の選挙区で高橋派を多数派にする必要があります。
2 番目の選挙区の青木派の 4 人を鞍替えさせると高橋君は 5 議席を獲得できます。このとき青木君の獲得する議席は 2 議席なので、高橋君は選挙に勝利できます。
入力例 3
3 3 4 2 1 2 3 7 2 6
出力例 3
0
青木派から高橋派に鞍替えする人が 0 人でも高橋君が選挙で勝つ場合は 0 人が答えになります。
入力例 4
10 1878 2089 16 1982 1769 13 2148 1601 14 2189 2362 15 2268 2279 16 2394 2841 18 2926 2971 20 3091 2146 20 3878 4685 38 4504 4617 29
出力例 4
86
Score : 400 points
Problem Statement
Takahashi and Aoki are competing in an election.
There are N electoral districts. The i-th district has X_i + Y_i voters, of which X_i are for Takahashi and Y_i are for Aoki. (X_i + Y_i is always an odd number.)
In each district, the majority party wins all Z_i seats in that district. Then, whoever wins the majority of seats in the N districts as a whole wins the election. (\displaystyle \sum_{i=1}^N Z_i is odd.)
At least how many voters must switch from Aoki to Takahashi for Takahashi to win the election?
Constraints
- 1 \leq N \leq 100
- 0 \leq X_i, Y_i \leq 10^9
- X_i + Y_i is odd.
- 1 \leq Z_i
- \displaystyle \sum_{i=1}^N Z_i \leq 10^5
- \displaystyle \sum_{i=1}^N Z_i is odd.
Input
The input is given from Standard Input in the following format:
N X_1 Y_1 Z_1 X_2 Y_2 Z_2 \vdots X_N Y_N Z_N
Output
Print the answer.
Sample Input 1
1 3 8 1
Sample Output 1
3
Since there is only one district, whoever wins the seat in that district wins the election.
If three voters for Aoki in the district switch to Takahashi, there will be six voters for Takahashi and five for Aoki, and Takahashi will win the seat.
Sample Input 2
2 3 6 2 1 8 5
Sample Output 2
4
Since there are more seats in the second district than in the first district, Takahashi must win a majority in the second district to win the election.
If four voters for Aoki in the second district switch sides, Takahashi will win five seats. In this case, Aoki will win two seats, so Takahashi will win the election.
Sample Input 3
3 3 4 2 1 2 3 7 2 6
Sample Output 3
0
If Takahashi will win the election even if zero voters switch sides, the answer is 0.
Sample Input 4
10 1878 2089 16 1982 1769 13 2148 1601 14 2189 2362 15 2268 2279 16 2394 2841 18 2926 2971 20 3091 2146 20 3878 4685 38 4504 4617 29
Sample Output 4
86
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
H 行 W 列のグリッド状に分割されたフィールドがあります。
北 (上側) から i 行目、西 (左側) から j 列目のマスは文字 A_{i, j} で表されます。各文字の意味は次の通りです。
.: 空きマス。進入できる。#: 障害物。進入できない。>,v,<,^: それぞれ東・南・西・北を向いている人がいるマス。進入できない。人の視線は 1 マス分の幅を持ち、人が向いている方向にまっすぐ伸び、障害物や別の人に遮られる。(入出力例 1 にある説明も参考にしてください。)S: スタート地点。進入できる。ちょうど 1 ヵ所だけ存在する。人の視線に入っていないことが保証される。G: ゴール地点。進入できる。ちょうど 1 ヵ所だけ存在する。人の視線に入っていないことが保証される。
ナオヒロくんはスタート地点にいて、東西南北への 1 マス分の移動を好きな回数行えます。ただし、進入できないマスへの移動やフィールドの外への移動はできません。
彼が人の視線に一度も入らずにゴール地点に到達できるか判定して、できる場合はそのために最小で何回の移動が必要か求めてください。
制約
- 2 \leq H, W \leq 2000
- A_{i,j} は
.,#,>,v,<,^,S,Gのいずれかである S,Gは A_{i, j} の中にちょうど 1 回ずつ現れる- スタート地点・ゴール地点はともに人の視線に入っていない
入力
入力は以下の形式で標準入力から与えられる。
H W
A_{1,1}A_{1,2}\dots A_{1,W}
A_{2,1}A_{2,2}\dots A_{2,W}
\vdots
A_{H,1}A_{H,2}\dots A_{H,W}
出力
ナオヒロ君が人の視線に一度も入らずにゴール地点に到達できる場合は、そのために必要な(最小の)移動回数を出力せよ。できない場合は -1 を出力せよ。
入力例 1
5 7 ....Sv. .>..... ....... >..<.#< ^G....>
出力例 1
15
入力例 1 について、1 人以上の視線に入っている空きマスを ! で表すと次の図のようになります。

いくつかのマスについて具体的に説明すると次のようになります。(ここで、北から i 行目、西から j 列目のマスを (i, j) と表します。)
- (2, 4) は (2, 2) にいる東を向いている人からの視線に入っているマスである。
- (2, 6) は (2, 2) にいる東を向いている人と (1, 6) にいる南を向いている人の 2 人の視線に入っているマスである。
- (4, 5) は誰の視線にも入っていないマスである。(4, 7) にいる西を向いている人の視線は (4, 6) の障害物に遮られていて、(4, 1) にいる東を向いている人の視線は (4, 4) の人に遮られている。
ナオヒロ君は進入できないマス・視線に入っているマスのどちらも通らずにゴール地点へ行く必要があります。
入力例 2
4 3 S.. .<. .>. ..G
出力例 2
-1
ナオヒロ君がゴール地点に到達できない場合は -1 を出力してください。
Score : 425 points
Problem Statement
There is a field divided into a grid of H rows and W columns.
The square at the i-th row from the north (top) and the j-th column from the west (left) is represented by the character A_{i, j}. Each character represents the following.
.: An empty square. Passable.#: An obstacle. Impassable.>,v,<,^: Squares with a person facing east, south, west, and north, respectively. Impassable. The person's line of sight is one square wide and extends straight in the direction the person is facing, and is blocked by an obstacle or another person. (See also the description at Sample Input/Output 1.)S: The starting point. Passable. There is exactly one starting point. It is guaranteed not to be in a person's line of sight.G: The goal. Passable. There is exactly one goal. It is guaranteed not to be in a person's line of sight.
Naohiro is at the starting point and can move one square to the east, west, south, and north as many times as he wants. However, he cannot enter an impassable square or leave the field.
Determine if he can reach the goal without entering a person's line of sight, and if so, find the minimum number of moves required to do so.
Constraints
- 2 \leq H, W \leq 2000
- A_{i,j} is
.,#,>,v,<,^,S, orG. - Each of
SandGoccurs exactly once among A_{i, j}. - Neither the starting point nor the goal is in a person's line of sight.
Input
The input is given from Standard Input in the following format:
H W
A_{1,1}A_{1,2}\dots A_{1,W}
A_{2,1}A_{2,2}\dots A_{2,W}
\vdots
A_{H,1}A_{H,2}\dots A_{H,W}
Output
If Naohiro can reach the goal without entering a person's line of sight, print the (minimum) number of moves required to do so. Otherwise, print -1.
Sample Input 1
5 7 ....Sv. .>..... ....... >..<.#< ^G....>
Sample Output 1
15
For Sample Input 1, the following figure shows the empty squares that are in the lines of sight of one or more people as !.

Let us describe some of the squares. (Let (i, j) denote the square in the i-th row from the north and the j-th column from the west.)
- (2, 4) is a square in the line of sight of the east-facing person at (2, 2).
- (2, 6) is a square in the lines of sight of two people, one facing east at (2, 2) and the other facing south at (1, 6).
- The square (4, 5) is not in anyone's line of sight. The line of sight of the west-facing person at (4, 7) is blocked by the obstacle at (4, 6), and the line of sight of the east-facing person at (4, 1) is blocked by the person at (4, 4).
Naohiro must reach the goal without passing through impassable squares or squares in a person's line of sight.
Sample Input 2
4 3 S.. .<. .>. ..G
Sample Output 2
-1
Print -1 if he cannot reach the goal.
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
整数 N,A_1,A_2,A_3 が与えられます。以下の 3 つの条件を全て満たすような正整数の組 (X_1,X_2,X_3) の個数を 998244353 で割ったあまりを求めてください。
- 全ての i で 1\leq X_i \leq N である。
- 全ての i で X_i は A_i の倍数である。
- (X_1 \oplus X_2) \oplus X_3 = 0 である。ただし、\oplus はビット単位の xor を表す。
ビット単位 xor とは
非負整数 A, B のビット単位 xor 、A \oplus B は、以下のように定義されます。- A \oplus B を二進表記した際の 2^k (k \geq 0) の位の数は、A, B を二進表記した際の 2^k の位の数のうち一方のみが 1 であれば 1、そうでなければ 0 である。
制約
- 1 \leq N \leq 10^{18}
- 1 \leq A_i \leq 10
- 入力は全て整数である
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 A_3
出力
答えを出力せよ。
入力例 1
13 2 3 5
出力例 1
4
(X_1,X_2,X_3) が (6,3,5),(6,12,10),(12,6,10),(12,9,5) のときの 4 通りが条件を満たします。
入力例 2
1000000000000000000 1 1 1
出力例 2
426724011
入力例 3
31415926535897932 3 8 4
出力例 3
759934997
Score : 500 points
Problem Statement
You are given integers N,A_1,A_2,A_3. Find the number, modulo 998244353, of triples of positive integers (X_1,X_2,X_3) that satisfy all of the following three conditions.
- 1\leq X_i \leq N for every i.
- X_i is a multiple of A_i for every i.
- (X_1 \oplus X_2) \oplus X_3 = 0, where \oplus denotes bitwise xor.
What is bitwise xor?
The bitwise xor of non-negative integers A and B, A \oplus B, is defined as follows.- When A \oplus B is written in binary, the 2^ks place (k \geq 0) is 1 if exactly one of the 2^ks places of A and B is 1, and 0 otherwise.
Constraints
- 1 \leq N \leq 10^{18}
- 1 \leq A_i \leq 10
- All input values are integers.
Input
The Input is given from Standard Input in the following format:
N A_1 A_2 A_3
Output
Print the answer.
Sample Input 1
13 2 3 5
Sample Output 1
4
Four triples (X_1,X_2,X_3) satisfy the conditions: (6,3,5),(6,12,10),(12,6,10),(12,9,5).
Sample Input 2
1000000000000000000 1 1 1
Sample Output 2
426724011
Sample Input 3
31415926535897932 3 8 4
Sample Output 3
759934997
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
N 行 M 列のグリッドがあります。上から i 行目左から j 列目のマスには整数 A_{i,j} が書かれています。
ここで、グリッドのマスに書かれている計 NM 個の整数は 1,\ldots,N をちょうど M 個ずつ含みます。
あなたは次の手順でマスに書かれた数を入れ替える操作を行います。
- i=1,\ldots,N の順に次を行う。
- i 行目に書かれた数を自由に並び替える。すなわち、1,\ldots,M の並び替えである長さ M の数列 P=(P_{1},\ldots,P_{M}) を自由に選び、A_{i,1},\ldots,A_{i,M} を 同時に A_{i,P_{1}},\ldots,A_{i,P_{M}} に置き換える。
あなたの目的は、操作後に全ての列が 1,\ldots,N を 1 つずつ含むようにすることです。そのようなことが可能であるか判定し、可能であれば操作後のグリッドの状態を出力してください。
制約
- 1 \leq N,M \leq 100
- 1 \leq A_{i,j} \leq N
- 入力は全て整数である
- NM 個の数 A_{1,1},\ldots,A_{N,M} は 1,\ldots,N をそれぞれちょうど M 個ずつ含む
入力
入力は以下の形式で標準入力から与えられる。
N M
A_{1,1} \ldots A_{1,M}
\vdots
A_{N,1} \ldots A_{N,M}
出力
操作により全ての列が 1,\ldots,N を 1 つずつ含むようにするのが不可能ならば No と出力せよ。
可能であるとき、1 行目に Yes と出力し、続く N 行に、全ての列が 1,\ldots,N を 1 つずつ含むように操作したあとのグリッドの状態を次の形式で出力せよ。
グリッドの上から i 行目左から j 列目のマスに書かれた数を B_{i,j} とする。各 1\leq i \leq N について i+1 行目に B_{i,1},\ldots,B_{i,M} をこの順に空白区切りで出力せよ。
答えが複数存在する場合、どれを出力しても正解とみなされる。
入力例 1
3 2 1 1 2 3 2 3
出力例 1
Yes 1 1 3 2 2 3
この他、以下の出力も正解とみなされる。
Yes 1 1 2 3 3 2
入力例 2
4 4 1 2 3 4 1 1 1 2 3 2 2 4 4 4 3 3
出力例 2
Yes 1 4 3 2 2 1 1 1 4 2 2 3 3 3 4 4
Score : 600 points
Problem Statement
There is a grid with N rows and M columns. The square at the i-th row from the top and the j-th column from the left contains the integer A_{i,j}.
Here, the squares contain M occurrences of each of 1,\ldots,N, for a total of NM integers.
You perform the following operations to swap the numbers written on the squares.
- For i=1,\ldots,N in this order, do the following.
- Freely rearrange the numbers written in the i-th row. That is, freely choose a permutation P=(P_{1},\ldots,P_{M}) of 1,\ldots,M, and replace A_{i,1},\ldots,A_{i,M} with A_{i,P_{1}},\ldots,A_{i,P_{M}} simultaneously.
Your goal is to perform the operations so that each column contains each of 1,\ldots,N once. Determine if this is possible, and if so, print such a resulting grid.
Constraints
- 1 \leq N,M \leq 100
- 1 \leq A_{i,j} \leq N
- All input values are integers.
- The NM numbers A_{1,1},\ldots,A_{N,M} contain exactly M occurrences of each of 1,\ldots,N.
Input
The Input is given from Standard Input in the following format:
N M
A_{1,1} \ldots A_{1,M}
\vdots
A_{N,1} \ldots A_{N,M}
Output
If it is impossible to perform the operations so that each column contains each of 1,\ldots,N once, print No.
Otherwise, print Yes in the first line, and in the subsequent N lines, print a resulting grid where each column contains each of 1,\ldots,N once, in the following format.
Let B_{i,j} be the number written in the square at the i-th row from the top and j-th column from the left of the grid. For each 1\leq i \leq N, the (i+1)-th line should contain B_{i,1},\ldots,B_{i,M} in this order, with spaces in between.
If multiple solutions exist, any of them is accepted.
Sample Input 1
3 2 1 1 2 3 2 3
Sample Output 1
Yes 1 1 3 2 2 3
Also, the following output is accepted.
Yes 1 1 2 3 3 2
Sample Input 2
4 4 1 2 3 4 1 1 1 2 3 2 2 4 4 4 3 3
Sample Output 2
Yes 1 4 3 2 2 1 1 1 4 2 2 3 3 3 4 4
実行時間制限: 8 sec / メモリ制限: 1024 MiB
配点 : 650 点
問題文
頂点に 1 から N までの番号がついた N 頂点の有向グラフがあります。グラフに多重辺は存在しませんが自己ループは存在する可能性があります。また、グラフに含まれる全ての辺は次の条件を満たします。
- 辺が頂点 s から頂点 t に向けて張られているとする。このとき s, t は 0 \leq t - s\leq 2 と t = 1 の少なくとも一方を満たす。
グラフの辺の有無は長さ N の数列 A,B,C,D によって表されます。A, B, C, D の各要素は次の意味を持ちます。(以下では A の n 番目の要素を A_n と表します。B_n, C_n, D_n も同様です)
- A_n は頂点 n から頂点 n に向けて辺が張られていたら 1 、そうでなければ 0
- B_n は頂点 n から頂点 n+1 に向けて辺が張られていたら 1 、そうでなければ 0 (ただし B_N = 0)
- C_n は頂点 n から頂点 n+2 に向けて辺が張られていたら 1 、そうでなければ 0 (ただし C_{N-1} = C_N = 0)
- D_n は頂点 n から頂点 1 に向けて辺が張られていたら 1 、そうでなければ 0 (ただし D_1 = A_1)
与えられたグラフにおいて、頂点 1 が始点、頂点 N が終点であり K 辺からなる walk の個数を 998244353 で割った余りを求めてください。
ここで「頂点 1 が始点、頂点 N が終点であり K 辺からなる walk 」とは、頂点の列 v_0 = 1, v_1, \dots, v_K = N であって、各 i (0 \leq i \lt K) について頂点 v_i から頂点 v_{i + 1} へ向かう辺があるものを言います。2 つの walk は列として異なる時に別々に数えます。
制約
- 2 \leq N \leq 5 \times 10^4
- 1 \leq K \leq 5 \times 10^5
- A_i, B_i, C_i, D_i \in \lbrace 0, 1 \rbrace
- A_1 = D_1
- B_N = C_{N-1} = C_N = 0
入力
入力は以下の形式で標準入力から与えられる。
N K A_1 A_2 \dots A_N B_1 B_2 \dots B_N C_1 C_2 \dots C_N D_1 D_2 \dots D_N
出力
頂点 1 が始点、頂点 N が終点であり K 辺からなる walk の個数を 998244353 で割った余りを出力せよ。
入力例 1
3 3 1 0 1 1 1 0 1 0 0 1 0 1
出力例 1
6
与えられるグラフを図示すると次のようになります。

条件を満たす walk は次の 6 個です。
- 1, 1, 1, 3
- 1, 1, 2, 3
- 1, 1, 3, 3
- 1, 2, 3, 3
- 1, 3, 1, 3
- 1, 3, 3, 3
入力例 2
4 6 1 1 1 1 1 1 1 0 1 1 0 0 1 0 0 0
出力例 2
50
入力例 3
10 500000 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 1 0 0 0 1 1 1 1 1 0 1 1 0
出力例 3
866263864
Score : 650 points
Problem Statement
We have a directed graph with N vertices numbered 1 to N. The graph has no multi-edges but can have self-loops. Also, every edge in the graph satisfies the following condition.
- If the edge goes from vertex s to vertex t, then s and t satisfy at least one of 0 \leq t - s\leq 2 and t = 1.
The presence or absence of an edge in the graph is represented by sequences A, B, C, D, each of length N. Each element of A, B, C, D has the following meaning. (Let A_n denote the n-th element of A; the same applies to B_n, C_n, D_n.)
- A_n is 1 if there is an edge from vertex n to vertex n, and 0 otherwise.
- B_n is 1 if there is an edge from vertex n to vertex n+1, and 0 otherwise. (Here, B_N = 0.)
- C_n is 1 if there is an edge from vertex n to vertex n+2, and 0 otherwise. (Here, C_{N-1} = C_N = 0.)
- D_n is 1 if there is an edge from vertex n to vertex 1, and 0 otherwise. (Here, D_1 = A_1.)
In the given graph, find the number, modulo 998244353, of walks with K edges starting at vertex 1 and ending at vertex N.
Here, a walk with K edges starting at vertex 1 and ending at vertex N is a sequence of vertices v_0 = 1, v_1, \dots, v_K = N such that for each i (0 \leq i \lt K) there is an edge from vertex v_i to vertex v_{i + 1}. Two walks are distinguished when they differ as sequences.
Constraints
- 2 \leq N \leq 5 \times 10^4
- 1 \leq K \leq 5 \times 10^5
- A_i, B_i, C_i, D_i \in \lbrace 0, 1 \rbrace
- A_1 = D_1
- B_N = C_{N-1} = C_N = 0
Input
The input is given from Standard Input in the following format:
N K A_1 A_2 \dots A_N B_1 B_2 \dots B_N C_1 C_2 \dots C_N D_1 D_2 \dots D_N
Output
Print the number, modulo 998244353, of walks of length K starting at vertex 1 and ending at vertex N.
Sample Input 1
3 3 1 0 1 1 1 0 1 0 0 1 0 1
Sample Output 1
6
The following figure shows the graph.

The following six walks satisfy the conditions.
- 1, 1, 1, 3
- 1, 1, 2, 3
- 1, 1, 3, 3
- 1, 2, 3, 3
- 1, 3, 1, 3
- 1, 3, 3, 3
Sample Input 2
4 6 1 1 1 1 1 1 1 0 1 1 0 0 1 0 0 0
Sample Output 2
50
Sample Input 3
10 500000 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 1 0 0 0 1 1 1 1 1 0 1 1 0
Sample Output 3
866263864