Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
小学生のたかはし君は、遠足で林にきています。遠足を楽しんでいる彼は、木が一直線に並んでいることに気づきました。 そして、授業で、「植木算」というものを習ったことを思い出しました。彼が授業で習った植木算の問題は、「木が 4 本 一直線に並んでいるとき、隣り合う木の"間"は何箇所存在するか。」というもので、その答えは図1の通り 3 箇所です。
今回、遠足中の彼が見ている光景は、その問題のシチュエーションとよく似通っていて、隣り合う木の間の数を数えたくなりました。 彼は遠足パンフレットに、一直線に生えている木々の本数が書かれていることに気づきました。しかし、彼は実際に木の間を数える手段しか知らないので、本数によってはとても時間がかかってしまうかもしれません。
そこで、あなたにお願いがあります。 一直線に並んでいる木々が n 本あるという情報が与えられるので、隣り合う木の間の数を出力するプログラムをたかはし君のために作ってあげてください。
入力
入力は以下の形式で標準入力から与えられる。
n
- 1 行目には、一直線に並んでいる木々の本数を表す整数 n (1 ≦ n ≦ 10,000) が与えられる。
出力
隣り合う木の間の数を 1 行に出力せよ。出力の末尾に改行をいれること。
入力例1
4
出力例1
3
問題文中で説明したケースであり、彼が授業で習った時の値設定です。
入力例2
100
出力例2
99
100本並んでいるので、間は99箇所あります。
入力例3
1
出力例3
0
1 本の木しかないので、0 と出力してください。

Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
文字列 A が与えられる。小文字アルファベット(a-z)のみを使って辞書順比較したとき文字列 A より小さいものを1つ何でも良いので出力せよ。ただし、文字列は 1 文字以上 100 文字以下でなければならない。もし存在しない場合は "-1" を出力せよ。
ただし、ある文字列 S=S_1S_2...S_n と T=T_1T_2...T_m について、辞書順比較した際に S<T であるとは、次のどちらか一方の状態が成り立っていることを言う。
- ある整数 i (1≦i≦{\rm min}(n,m)) に関して、 1≦j≦i−1 を満たすどの整数 j に関しても S_j=T_j が成立し、かつ S_i<T_i が成立する
- 任意の整数 i (1≦i≦{\rm min}(n,m)) に関して、 常に S_i=T_i が成立し、かつ |S|<|T| である。ただし |X| は文字列 X の長さを表すものとする。
なにやら頭が痛くなる記述だが、言い換えると次の通りである。
- それぞれの文字列の同じ位置同士を先頭から比較していって、初めて不一致になったら、その文字同士の(アルファベットでの)比較結果が文字列の全体の比較結果である。 例えば、"abcd" と "ax" を比較すると、2 文字目で、'b'<'x' となるので、"abcd"<"ax" である。
- もし、比較している途中で片方の文字列が尽きてしまったら、文字列の長さが短い方が小さい。例えば "ab" < "abc"である。
入力
入力は以下の形式で標準入力から与えられる。
A
- 1 行目には、文字列 A (1 ≦ |A| ≦ 11) が与えられる。|A|は文字列 |A| の長さを表す。Aは小文字アルファベット(a-z)のみから成る。
出力
文字列 A より小さい文字列を 1 つ 1 行に出力せよ。ただし、小文字アルファベット(a-z)のみを用いており、長さは1以上100以下でなければならない。解が複数ある場合はどれを出力しても良い。存在しない場合は、代わりに "-1" を出力すること。出力の末尾に改行をいれること。
入力例1
xyz
出力例1
xy
もちろん、"xy" の他に、"abcd" 等を出力しても正答として扱われる。
入力例2
c
出力例2
b
"a" もしくは "b" が正答として扱われる。
入力例3
a
出力例3
-1
"a" より小さい文字列は存在しない。出力する文字列は長さ1以上でなければならないため、""(空文字列)は不適切であることに注意せよ。
入力例4
aaaaa
出力例4
aaaa
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
たかはし君は迷路が好きです。今、上下左右に移動できる二次元盤面上の迷路を解こうとしています。盤面は以下のような形式で与えられます。
- まず、盤面のサイズと、迷路のスタート地点とゴール地点の座標が与えられる。
- 次に、それぞれのマスが通行可能な空きマス(
.)か通行不可能な壁マス(#)かという情報を持った盤面が与えられる。盤面は壁マスで囲まれている。スタート地点とゴール地点は必ず空きマスであり、スタート地点からゴール地点へは、空きマスを辿って必ずたどり着ける。具体的には、入出力例を参考にすると良い。
今、彼は上記の迷路を解くのに必要な最小移動手数を求めたいと思っています。どうやって求めるかを調べていたところ、「幅優先探索」という手法が効率的であることを知りました。幅優先探索というのは以下の手法です。
- スタート地点から近い(たどり着くための最短手数が少ない)マスから順番に、たどり着く手数を以下のように確定していく。説明の例として図1の迷路を利用する。
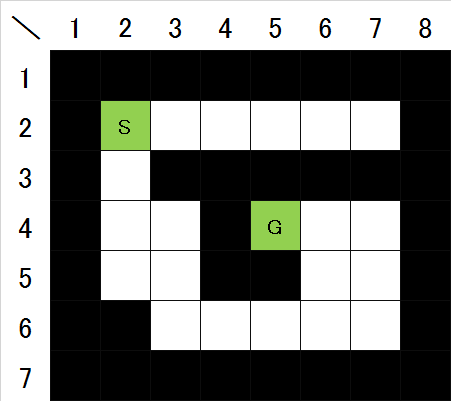
- 最初に、スタート地点は、スタート地点から手数0でたどり着ける(当然)ので、最短手数0で確定させる(図2)。
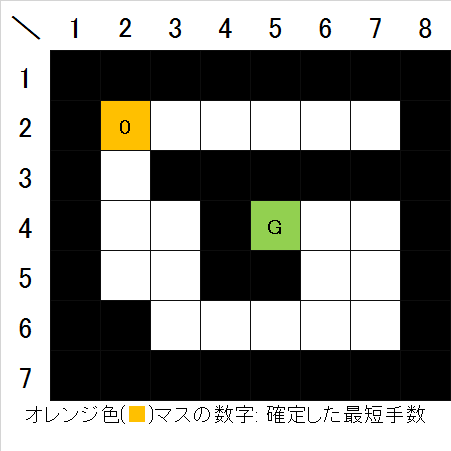
- 次に、スタート地点の四近傍(上下左右)の空きマスについて、手数1で確定させる(図3)。
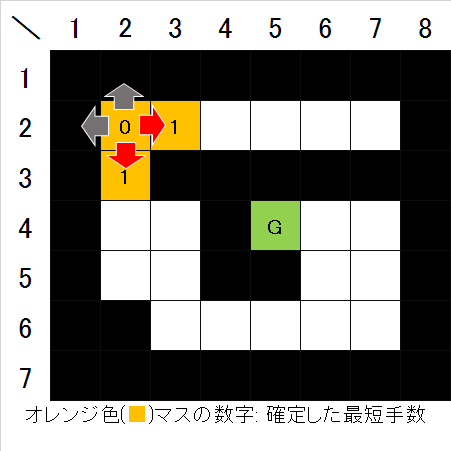
- 次に、手数1で確定したそれぞれのマスの4近傍を見て、まだ確定していない空きマスがあればそのマスを手数2で確定させる(図4)。
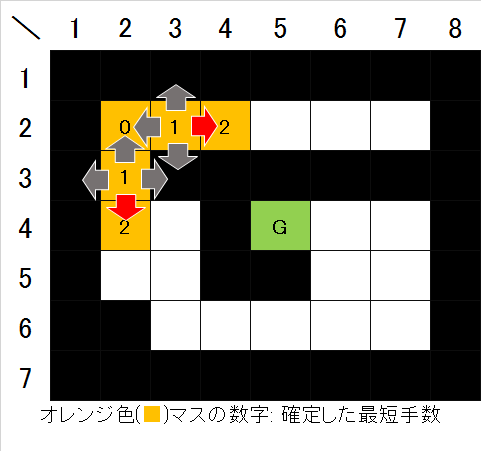
- 次に、手数2で確定したそれぞれのマスの4近傍を見て、まだ確定していない空きマスがあればそのマスを手数3で確定させる(図5)。
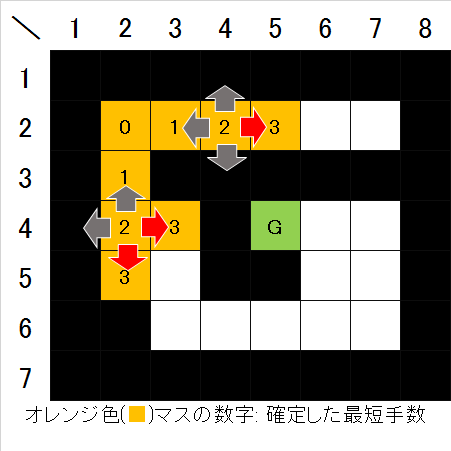
- 次に、手数3で確定したそれぞれのマスの4近傍を見て、まだ確定していない空きマスがあればそのマスを手数4で確定させる(図6)。
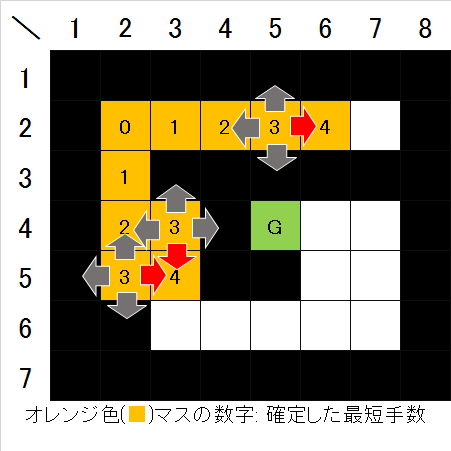
- 上記の手順を確定の更新が無くなるまで繰り返すと、スタート地点からたどり着ける全ての空きマスについて最短手数が確定する(図7)。スタートとゴールは必ず空きマスを辿ってたどり着けるという制約があるので、ゴール地点への最短手数も分かる。

さて、この処理をスマートに実装するためには、先入れ先出し(FIFO)のキュー(Queue)というデータ構造を用いると良いことが知られています。もちろん、使わなくても解くことは可能です。今回、よく分からなければ思いついた方法で解くことをおすすめします。先入れ先出しのキューとは以下のような機能を持つデータ構造です。
- 追加(Push): キューの末尾にデータを追加する。
- 取り出し(Pop): キューの先頭のデータを取り出す。
このデータ構造を使うと、先ほどの幅優先探索の説明における「マスの最短手数の確定」のタイミングでその確定マスをキューに追加し、追加操作が終わればPopを行い、取り出したマスの4近傍を調べるということを繰り返せば(つまり先に追加されたものから順番に処理していけば)、簡潔に処理ができることが分かります。
入力
入力は以下の形式で標準入力から与えられる。
R\ C
sy\ sx
gy\ gx
c_{(1,1)}c_{(1,2)}\ …\ c_{(1,C)}
c_{(2,1)}c_{(2,2)}\ …\ c_{(2,C)}
:
c_{(R,1)}c_{(R,2)}\ …\ c_{(R,C)}
- 1 行目には、行数 R(1≦R≦50)と列数 C(1≦C≦50)がそれぞれ空白区切りで与えられる。
- 2 行目には、スタート地点の座標 (sy,sx) が空白区切りで与えられる。スタート地点が sy 行 sx 列にあることを意味する。 1≦sy≦R かつ 1≦sx≦C である。
- 3 行目には、ゴール地点の座標 (gy,gx) が空白区切りで与えられる。ゴール地点が gy 行 gx 列にあることを意味する。 1≦gy≦R かつ 1≦gx≦C であり、(gy,gx)≠(sy,sx)であることが保障されている。
- 4 行目から R 行、長さ C の文字列が 1 行ずつ与えられる。各文字は
.もしくは#のいずれかであり、i 回目 (1≦i≦R) に与えられられる文字列のうち j 文字目 (1≦j≦C) について、その文字が.なら、マス (i,j) が空きマスであり、#なら、マス (i,j) が壁マスであることをあらわす。 - 盤面は壁マスで囲まれている。つまり、i=1,i=R,j=1,j=C のうちいずれか1つでも条件を満たすマス (i,j) について、c_{(i,j)} は
#である。また、スタート地点とゴール地点は必ず空きマスであり、スタート地点からゴール地点へは、空きマスを辿って必ずたどり着ける。
出力
- スタート地点からゴール地点に移動する最小手数を 1 行に出力せよ。最後に改行を忘れないこと。
入力例1
7 8 2 2 4 5 ######## #......# #.###### #..#...# #..##..# ##.....# ########
出力例1
11
問題文中の例です。
入力例2
5 8 2 2 2 4 ######## #.#....# #.###..# #......# ########
出力例2
10
図8のように進めば 10 手でたどり着くことが進むことができます(※Sはスタート、Gはゴールをあらわす)。

入力例3
50 50 2 2 49 49 ################################################## #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# #................................................# ##################################################
出力例3
94
もはやただの広い空間であり、迷路と呼んで良いのかは分からないがこの問題でこのような盤面も迷路として扱う。兎にも角にも、スタートからゴールへの最短手数は 94 である。
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
たかはし王国の国王であるたかはし君主は数字の 4 と 9 が大嫌いです。それらの数字を国内で目にするだけで気分が悪いので、それらを使ってはいけないという法律を定めました。この法律を破ってしまうと罰せられます。数字が禁止されているので、ある数の10進表現を考えたとき、いずれかの桁に禁止された数字が1つでも含まれている場合、その数を使うことはできません。
今まで使っていた数字を使えなくなったあなたは、うっかり使ってしまって罰せられては困るので、使う可能性がある数の区間 [A,B]=\{A,A+1,A+2,...,B\} に、いくつ禁止された数が含まれているかを確かめることにしました。そのためのプログラムを作ってください。
部分点
この問題には2つのデータセットがあり、データセット毎に部分点が設定されている。
- 1 ≦ A ≦ B ≦ 10,000 を満たすデータセット 1 に正解した場合は 30 点が与えられる。
- 追加制約のないデータセット 2 に正解した場合は、上記のデータセットとは別に 70 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
A B
- 1 行目には、整数 A,B (1≦A≦B≦10^{18}) が空白区切りで与えられる。
出力
区間 [A,B] に含まれる禁止された数がいくつ含まれているかを 1 行に出力せよ。出力の末尾に改行をいれること。
入力例1
1 9
出力例1
2
4 と 9 が禁止されています。
入力例2
40 49
出力例2
10
40 ~ 49 は全て禁止された数です。
入力例3
1 1000
出力例3
488
入力例4
1 1000000000000000000
出力例4
981985601490518016