Time Limit: 20 sec / Memory Limit: 1024 MiB
配点 : 100 点
うさぎは昨年や一昨年や一昨々年のように,Xmas Contest 2021 を記念した看板を作ろうとしている.
うさぎがアバンギャルドなデザインを考えたところで,きつね 0 ときつね 1 がやってきて「今年は自分たちも看板作りに携わりたい」と言ってきたので,うさぎはきつねたちと一緒に面白い看板を作ることにした.
問題文
この問題は interactive である.採点用プログラムが最大で 実行時間 100 ms / メモリ 8 MB 程度を使用する.
横 500 px,縦 500 px のキャンバスがあり,画素の位置は整数の組 (x, y) (0 \leq x < 500,0 \leq y < 500) で表される.x 座標が増える方向が左から右へ,y 座標が増える方向が上から下であることに注意せよ.各画素は白か黒かのいずれかである.はじめ,キャンバスのどの画素も白である.
いま,きつね 0 ときつね 1 がともに巨大な鉛筆を抱えた状態で画素 (0, 0) にいる.以下の操作を高々 10\,000 回行うことで,与えられる目標のデザインに沿った画像を作り上げたい.
- 操作: 画素 (x, y) を指定し,「きつねさんは画素 (x, y) へ移動してください」と声をかける.すると,きつね 0 ときつね 1 のうち等確率でランダムに選ばれた一方が画素 (x, y) へ移動する.すでに (一方または双方の) きつねがいる画素を指定して操作を行っても構わない.
きつねは移動するときに,移動前の画素から移動後の画素へと黒い線分を引く.厳密には,ブレゼンハムのアルゴリズムによって線分の通る画素を求め,そのすべての画素を黒へと変える.(詳細は配布されるローカル用テスターの実装も参考にせよ)

今年の看板のデザイン
達成条件
目標のデザインは横 500 px,縦 500 px の白黒画像として与えられる.操作によって作られた画像が以下の 2 条件をどちらも満たしていれば「デザインに沿った」とみなされる:
- 目標のデザインにおいて黒であるような画素のうち,作られた画像においても黒であるような画素の割合が 85% 以上であること.
- 目標のデザインにおいて白であるような画素のうち,作られた画像においても白であるような画素の割合が 70% 以上であること.
データ
この問題を解くために必要なデータをまとめた zip ファイルがこちらからダウンロードできる.zip 内には以下のファイルが入っている.
atrandom/input.png: 目標デザインを表す画像.画像サイズは横 500 px,縦 500 px である.atrandom/input.txt: 目標デザインを下記の入出力の仕様に合わせてテキストファイル化したもの.実際の採点時に提出されたプログラムに最初に与えられる入力と同一である.atrandom/interactive_tester.py: この問題における interactive なやりとりをローカルでテストするための Python 3 製ツール.python3 interactive_tester.py <input_file> <seed> -- <cmd_line_solution>として使用する.<input_file>は目標デザインをテキスト化したもののファイルパス.実際の採点と同様のケースでテストするには,同梱されているinput.txtを指定すればよい.<seed>は移動するきつねを決める際に用いられる乱数のシード.本ツールで用いられている乱数生成方法は実際の採点時に用いられるものとは必ずしも一致しない.<cmd_line_solution>はあなたの提出するプログラムを実行するためのコマンドを表す文字列.
- たとえば C++ で書かれた解答を本ツールと同じディレクトリでコンパイルして
solver.outという実行可能ファイルを作った場合,python3 interactive_tester.py input.txt 0 -- ./solver.outなどとして実行できる. - 同様にたとえば Python で書かれた
solver.pyという解答を本ツールと同じディレクトリに置いた場合,python3 interactive_tester.py input.txt 0 -- python solver.pyなどとして実行できる. - なお,このツール内にある
drawline関数はブレゼンハムのアルゴリズムを実装したものとなっている.解答の作成時などに参考にしてもよい.
atrandom/visualize.html: ローカル用のテストツールが出力した詳細な画像データを見るためのビジュアライザ.- ローカル用テストツールが正しく実行されると,
interactive_tester.dumpというファイルが同じ階層に生成される.このファイルをビジュアライザに与えることで,あなたのプログラムが作った画像を可視化し,画像として保存することができる.
- ローカル用テストツールが正しく実行されると,
入出力
- 整数 W,H,T が空白区切りで標準入力に与えられる.
- これは目標のデザインおよびキャンバスが横 W px,縦 H px からなり,高々 T 回の操作を行ってよいことを表す.
- すなわち,この問題の入力においては W = 500,H = 500,T = 10\,000 を満たす.
.および#のみからなる W 文字の文字列が H 行にわたって標準入力に与えられる.- このうち y 行目 (0 \leq y < H) の文字列の x 文字目 (0 \leq x < W) は,目標のデザインにおける画素 (x, y) の色を表す.白は
.,黒は#によって表される.
- このうち y 行目 (0 \leq y < H) の文字列の x 文字目 (0 \leq x < W) は,目標のデザインにおける画素 (x, y) の色を表す.白は
- 以下を (最大で) T 回繰り返す.
- あなたのプログラムは 2 つの整数 x, y を空白区切りで標準出力に出力しなければならない.
- (x, y) = (-1, -1) のとき,これ以上操作を行わないことを示し,繰り返しを終了する.これ以降,入力が与えられることはない.
- そうでないとき,0 \leq x < W かつ 0 \leq y < H でなければならず,画素 (x, y) を指定して操作を行うことを示す.
- 操作の結果,きつね k (k = 0, 1) が動いたとすると,整数 k が標準入力に与えられる.
- あなたのプログラムは 2 つの整数 x, y を空白区切りで標準出力に出力しなければならない.
入出力例も参考にせよ.
注意点
すべての操作を終えた後,あなたのプログラムは直ちに終了しなければならない.終了しなかった場合のジャッジ結果は不定である.また,条件を満たさない不正な出力をした場合の結果も不定である (必ずしも WA になるとは限らない).
すべての操作を終えてあなたのプログラムが終了した後,作られた画像が達成条件を満たしていれば正答とみなされる.
出力した後に,出力を flush しなければならないことに注意せよ.flush しなかった場合,TLE となることがある.
各言語での入出力の方法は過去の AtCoder で出題されている問題 (リンク: ABC 019 D: 高橋くんと木の直径) を参考にするとよい。
入出力例
W=5,\ H=5,\ T=10 のときの入出力例を示す.
実際のテストケースとして与えられる入力データは配布データに含まれるものと同一な 1 ケースのみであり,以下は入出力の具体例を示すための説明であることに注意せよ.
| 入力 | 出力 | 説明 |
|---|---|---|
5 5 10 |
W, H, T が与えられている. | |
..##. |
目標のデザインが与えられている. | |
2 4 |
(x, y) = (2, 4) として操作を行う. | |
1 |
操作の結果,動いたのはきつね 1 であるという情報が与えられる. | |
3 3 |
(x, y) = (3, 3) として操作を行う. | |
1 |
操作の結果,動いたのはきつね 1 であるという情報が与えられる. | |
3 0 |
(x, y) = (3, 0) として操作を行う. | |
0 |
操作の結果,動いたのはきつね 0 であるという情報が与えられる. | |
-1 -1 |
これ以上の操作は行わない (操作を 3 回で終える) ことを示す. |
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
ごきげんななめというパズルがうまく解けずごきげんななめになってしまったうなぎは,パズルの盤面に自身や友達の魚を描いて遊んでいました.
問題文
正の整数 M, N が与えられる.M 行 N 列のマス目があり,各マスは正方形である.
これから,各マスに対角線のうちちょうど 1 つを書き込む.このとき,無向グラフであって,いずれかのマスの頂点であるような (M + 1) (N + 1) 個の点をグラフの頂点とし,書き込まれた対角線をグラフの辺とするものを考え,その連結成分の個数を書き込み方の得点と呼ぶ.得点としてあり得る最小値と最大値を求めよ.

得点が 10 となる例
制約
- 1 \le M \le 10^9.
- 1 \le N \le 10^9.
入力
入力は以下の形式で標準入力から与えられる.
M N
出力
得点としてあり得る最小値 a と最大値 b を以下の形式で出力せよ.
a b
入力例 1
2 3
出力例 1
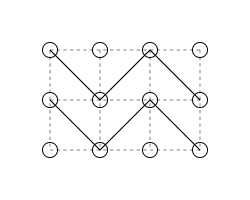
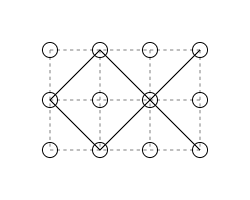
6 7
得点が 6 となる例と得点が 7 となる例を以下の図に示す.
Time Limit: 5 sec / Memory Limit: 1024 MiB
配点 : 100 点
シマウマの縞は一世代ごとに一か所が増えるという伝説があるので,その変化の過程を数えてください.
問題文
文字 0, 1, ? からなる長さ N の文字列 S が与えられる.文字列の N + 1 個組 (t_0, t_1, \ldots, t_N) であって以下の条件をすべて満たすものの個数を 998244353 で割った余りを求めよ:
- t_0 は空文字列である.
- 各 i = 0, 1, \ldots, N - 1 に対し,t_{i+1} は,t_i に
0または1を 1 個いずれかの場所に挿入して得られる文字列である. - t_N は,S に現れる
?をそれぞれ0または1で置き換えて得られる文字列である.
制約
- 1 \le N \le 250\,000.
- S は
0,1,?からなる長さ N の文字列である.
部分点
- N \le 5\,000 を満たすデータセットに正解した場合は,10 点が与えられる.
- 追加制約のないデータセットに正解した場合は,上記とは別に 90 点が与えられる.
入力
入力は以下の形式で標準入力から与えられる.
N S
出力
個数を 998244353 で割った余りを出力せよ.
入力例 1
3 01?
出力例 1
8
条件を満たす組 (t_0, t_1, t_2, t_3) は以下の 8 個である:
- t_0 が空文字列,t_1 が
0,t_2 が00,t_3 が010. - t_0 が空文字列,t_1 が
0,t_2 が01,t_3 が010. - t_0 が空文字列,t_1 が
0,t_2 が01,t_3 が011. - t_0 が空文字列,t_1 が
0,t_2 が10,t_3 が010. - t_0 が空文字列,t_1 が
1,t_2 が01,t_3 が010. - t_0 が空文字列,t_1 が
1,t_2 が01,t_3 が011. - t_0 が空文字列,t_1 が
1,t_2 が10,t_3 が010. - t_0 が空文字列,t_1 が
1,t_2 が11,t_3 が011.
入力例 2
9 0??001011
出力例 2
32400
入力例 3
40 1111111111111111111100000000000000000000
出力例 3
88808106
Time Limit: 5 sec / Memory Limit: 1024 MiB
配点 : 100 点
昨年の問題に味を占めて行列式の問題を考えていたうさぎは,あるとき行列の成分に行列を入れてしまい……
問題文
整数を成分とする N 個の K \times K 行列 A_1, \ldots, A_N が与えられる.A_h の (i, j) 成分は A_{h,i,j} である (1 \le h \le N,1 \le i \le K,1 \le j \le K).
\mathfrak{S}_N を N 次対称群とする.K \times K 行列 \sum_{\sigma\in\mathfrak{S}_N} \operatorname{sgn}(\sigma) A_{\sigma(1)} \cdots A_{\sigma(N)} の各成分を 998244353 で割った余り (0 以上 998244353 未満) を求めよ.
(すなわち,A_1, \ldots, A_N の並べ替え N! 通りについて,その順の行列積に置換の符号をかけて足したものについて,各成分を 998244353 で割った余りを求めよ.)
制約
- 1 \le N \le 32.
- 1 \le K \le 8.
- 0 \le A_{h,i,j} < 998244353 (1 \le h \le N,1 \le i \le K,1 \le j \le K).
入力
入力は以下の形式で標準入力から与えられる.
N K
A_{1,1,1} \cdots A_{1,1,K}
\vdots
A_{1,K,1} \cdots A_{1,K,K}
\vdots
\vdots
\vdots
A_{N,1,1} \cdots A_{N,1,K}
\vdots
A_{N,K,1} \cdots A_{N,K,K}
出力
求める和の (i, j) 成分を 998244353 で割った余りを b_{i,j} として (1 \le i \le K,1 \le j \le K),以下の形式で出力せよ.
b_{1,1} \cdots b_{1,K}
\vdots
b_{K,1} \cdots b_{K,K}
入力例 1
2 3 2 7 1 8 2 8 1 8 2 8 4 5 9 0 4 5 2 3
出力例 1
31 998244259 998244344 100 998244306 55 61 998244298 16
A_1 A_2 - A_2 A_1 = \begin{bmatrix} 31 & -94 & -9 \\ 100 & -47 & 55 \\ 61 & -55 & 16 \end{bmatrix} となる.
入力例 2
3 2 30 10 40 10 50 90 20 60 50 30 50 80
出力例 2
155000 122000 67000 364000
A_1 A_2 A_3 - A_1 A_3 A_2 - A_2 A_1 A_3 + A_2 A_3 A_1 + A_3 A_1 A_2 - A_3 A_2 A_1 = \begin{bmatrix} 155000 & 122000 \\ 67000 & 364000 \end{bmatrix} となる.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
ハムスターは,滑車を回して等間隔に印をつけるのが趣味なので,永遠に続けられるようにしました.
問題文
e = 2.718\cdots を自然対数の底,\pi = 3.141\cdots を円周率とする.
正の整数 n に対し,実数 f(n) を以下のように定める.座標平面上の中心 (0, 0) 半径 1 の円 C を考える.C 上の点 P_0, P_1, \ldots, P_{n-1} を,P_j の座標を (\cos(2 \pi e j), \sin(2 \pi e j)) として定める (j = 0, 1, \ldots, n - 1).P_0, P_1, \ldots, P_{n-1} は相異なることが証明できるので,C はこれらの点によって n 個の弧に分かれる.それらの長さのうちの最大値を f(n) とする.
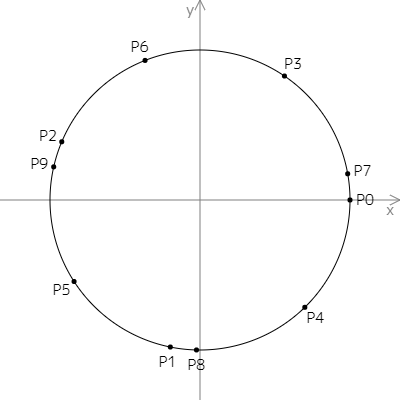
n = 10 のときの様子
f(n) > f(n + 1) を満たす正の整数 n は無限個存在することが証明できる.それらを昇順に n_1, n_2, \ldots とする.
正の整数 K が与えられる.f(n_K) = 2 \pi (a + e b) を満たす整数 a, b が一意に存在することが証明できる.n_K, a, b をそれぞれ 998244353 で割った余り (0 以上 998244353 未満) を求めよ.
制約
- 1 \le K \le 10^{11}.
入力
入力は以下の形式で標準入力から与えられる.
K
出力
n_K, a, b をそれぞれ 998244353 で割った余りを順に出力せよ.
入力例 1
1
出力例 1
1 1 0
n_1 = 1,f(1) = 2 \pi である.
入力例 2
2
出力例 2
2 998244351 1
n_2 = 2,f(2) = 2 \pi (-2 + e) である.
入力例 3
5
出力例 3
10 998244345 3
n_5 = 10,f(10) = 2 \pi (-8 + 3 e) である.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
シマウマ氏は,迷路に迷い込みました.迷路の中には,迷路と迷路がありました.
問題文
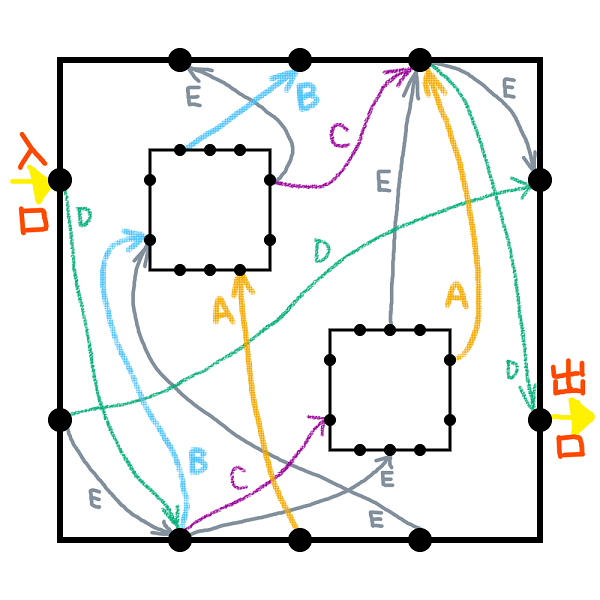
迷路
上図の迷路を解き,入口から出口への道筋で通った道に書かれた文字を順に並べた文字列を出力せよ.さらに,この文字列から E をすべて除いたものが回文となるようにせよ (この条件を満たさない場合は部分点が与えられる).
詳細を以下に示す.
- 黒丸で示された地点の間を,矢印で表された一方通行の道によって移動できる.
- 図において交差していても,黒丸以外で他の道に移ることはできない.
- 内側の 2 個の正方形の中には,再帰的に外側の正方形の中と同じ構造が同じ向きに入っている.
- 最も外側の入口の頂点から最も外側の出口の頂点へ (すなわち,図に直接示された入口から図に直接示された出口へ) 辿り着かなければならない.
- 道に書かれた文字は,矢印の傍に矢印と同じ色で示されており,
A,B,C,D,Eのいずれかである. - 1 個の黒丸から出ている道に書かれた文字はすべて異なることが (内側,その内側,……の黒丸についても) 証明できる.
- 出力する文字列の長さは 1 以上 10^5 以下でなければならない.
部分点
- 正しく迷路を解いた文字列を出力した場合は,10 点が与えられる.
- さらに,その文字列から
Eをすべて除いたものが回文となる場合は,上記とは別に 90 点が与えられる.
入力
入力は空である.
出力
入口から出口への道筋で通った道に書かれた文字を順に並べた文字列を出力せよ.
形式が正しいが不正解となる出力例を以下に示す.
ABACABADABACABAEABACABADABACABA
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
うさぎたちは黒板の整数を書き換えるときも美しさにこだわります.
問題文
1 個の入力ファイルにつき T 個のテストケースが与えられる.各テストケースで整数 N と整数 A_1, A_2, \ldots, A_N が与えられるので,以下の問に答えよ.
黒板に N 個の相異なる非負整数が書かれており,そのうち i 個目の値は A_i である (1 \le i \le N).
今から,くろうさとしろうさがゲームをする.くろうさが先手で,交互に以下の行動をする.
行動.黒板に書かれている数の中から 1 個を選び,それをより小さい別の非負整数に書き換える.ただし,書き換えた後も,黒板に書かれている N 個の数は相異なる必要がある.
行動ができなくなった方が負けで,負けなかった方が勝ちである.くろうさとしろうさのどちらに必勝法があるか?
制約
- 1 \le T \le 50.
- 2 \le N \le 50.
- 0 \le A_1 < A_2 < \cdots < A_N \le 10^{18}.
入力
標準入力の 1 行目にテストケースの個数 T が与えられる.その後,T 個のテストケースがそれぞれ以下の形式で与えられる.
N A_1 A_2 \cdots A_N
出力
各テストケースについて,くろうさに必勝法がある場合は Black,しろうさに必勝法がある場合は White を 1 行に出力せよ.
入力例 1
4 2 1 2 2 2 3 3 2 4 5 3 3 6 7
出力例 1
Black White White Black
1 番目のテストケースでは,くろうさが最初の行動で 2 を 0 に書き換えると,次のターンでしろうさが行動できないため,くろうさが勝つ.よってくろうさに必勝法がある.
Time Limit: 5 sec / Memory Limit: 1024 MiB
配点 : 100 点
昨年の問題を見て,無向グラフだけでなく有向グラフの積についても勉強したパンダは,合宿で出された宿題のことを思い出しました.
問題文
M \times N 頂点の有向グラフ G が次のように与えられる.G の頂点は整数の組 (i, j) (1 \le i \le M,1 \le j \le N) で表される.G の辺は以下の通りである:
- 各 i, j, k (1 \le i, k \le M,1 \le j \le N) について,頂点 (i, j) から頂点 (k, j) へ向かう辺が A_{i,k} 本存在する.
- 各 i, j, l (1 \le i \le M,1 \le j, l \le N) について,頂点 (i, j) から頂点 (i, l) へ向かう辺が B_{j,l} 本存在する.
G の各頂点について,それを根とする全域木の個数を 998244353 で割った余りを求めよ.ただし,頂点 v を根とする全域木とは,G の辺集合の大きさ (M \times N - 1) の部分集合であって,頂点 v から他のすべての頂点へ,それらの辺を辿って到達できるようなものを指す.また,すべての辺は互いに区別できるものとする.
制約
- 2 \le M \le 500.
- 2 \le N \le 500.
- 0 \le A_{i,k} < 998244353 (1 \le i, k \le M).
- A_{i,i} = 0 (1 \le i \le M).
- 0 \le B_{j,l} < 998244353 (1 \le j, l \le N).
- B_{j,j} = 0 (1 \le j \le N).
入力
入力は以下の形式で標準入力から与えられる.
M N
A_{1,1} A_{1,2} \cdots A_{1,M}
A_{2,1} A_{2,2} \cdots A_{2,M}
\vdots
A_{M,1} A_{M,2} \cdots A_{M,M}
B_{1,1} B_{1,2} \cdots B_{1,N}
B_{2,1} B_{2,2} \cdots B_{2,N}
\vdots
B_{N,1} B_{N,2} \cdots B_{N,N}
出力
G の頂点 (i, j) を根とする全域木の個数を 998244353 で割った余りを c_{i,j} として (1 \le i \le M,1 \le j \le N),以下の形式で出力せよ.
c_{1,1} c_{1,2} \cdots c_{1,N}
c_{2,1} c_{2,2} \cdots c_{2,N}
\vdots
c_{M,1} c_{M,2} \cdots c_{M,N}
入力例 1
2 2 0 1 0 0 0 0 1 0
出力例 1
0 2 0 0
入力例 2
3 4 0 1 1 1 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0
出力例 2
5647152 5647152 5647152 5647152 5647152 5647152 5647152 5647152 5647152 5647152 5647152 5647152
入力例 3
8 7 0 135281516 667138242 534705053 894609006 363845551 983263711 368399563 706521153 0 205503439 17581194 48971395 248346723 723069160 809331769 95374102 177083480 0 966474089 652931117 138712346 184755987 158919475 378114185 853217671 858087623 0 385823507 528768155 637814125 154972838 19176284 943976794 592288689 814797836 0 36241010 768079008 314765803 951276099 885340801 394097671 282385830 497465585 0 69878345 741774067 106863220 613773019 880926179 252272587 687103226 598098347 0 464666892 209619802 423789973 917284938 456850501 156569668 254002916 550388735 0 0 374063803 312003894 140142446 439797362 925129489 698118121 224246820 0 481191147 684671827 698236806 587586359 495418696 389630714 220172615 0 865126951 43296181 113977262 779586506 686309670 840140432 20859844 0 68039199 899714832 282973414 779591352 625690436 674759197 529126191 0 797360620 123804494 621741551 994747737 802674384 746120527 131201061 0 390573239 715533801 898645859 794564126 102532744 421471382 705169995 0
出力例 3
131557205 340211781 754428084 483092626 214955141 879575978 855361045 154851590 609864261 593925945 419466834 304837127 133113507 736477090 54632615 194927386 72101830 731318386 879946775 993433194 425542545 482048637 5880376 457649402 761233161 514923047 377996184 873772583 675269156 634883332 185904773 77524684 888694113 590920163 138406866 935188259 349594389 150776180 792068517 879123091 904461829 898840329 950638863 89008070 933320378 534103502 190891412 830891397 981135229 848888881 417544354 637718293 793237398 440680172 52239789 963945205
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
くろうさ「今年は一緒に遊ぼう!」
しろうさ「これって左手と右手にハンマー持てばひとりでできない?」
くろうさ「手だとねじれっちゃったりしてよくないからね」
しろうさ「かしこい」
もぐらたたき神「わしの速さの半分も出せんとは情けない」
くろうさ・しろうさ「……」
問題文
この問題は interactive である.採点用プログラムが最大で 実行時間 100 ms / メモリ 16 MB 程度を使用する.
2 行 100 列のマス目がある.i 行 j 列のマスを (i, j) と表す (1 \le i \le 2,1 \le j \le 100).
くろうさとしろうさがマス目にいて,最初にいるマスがそれぞれ (A, B), (C, D) として与えられる.
続いて,もぐらたたきが始まる.クエリにオンラインで応答せよ.各クエリは以下のいずれかである:
- もぐらがマス (e, f) に現れる.あなたはくろうさかしろうさを選ぶ.選ばれたうさぎがもぐらが現れたマスに移動する.うさぎがマス (i, j) からマス (e, f) に移動した場合,\lvert i - e \rvert + \lvert j - f \rvert のコストがかかる.
- もぐらたたきを終了する.このとき,今までにかかったコストの合計は,「もぐらが現れたマスの列を事前に知っていたと仮定したときのかかるコストの合計の最小値」を z として 2 z + \lvert A - C \rvert + \lvert B - D \rvert 以下でなければならない.
どの時点においても,くろうさ・しろうさ・もぐらのうち複数が同じマスにいることは認められる.
また,ジャッジは adaptive である.すなわち,あなたの選択によって,もぐらたたきが終了するかどうかやもぐらが現れるマスが変化する可能性がある.
制約
- 1 \le A \le 2.
- 1 \le B \le 100.
- 1 \le C \le 2.
- 1 \le D \le 100.
- もぐらが現れるマス (e, f) は 1 \le e \le 2,1 \le f \le 100 を満たす.
- もぐらが現れるクエリの回数は 1 以上 10\,000 以下である.
入出力
- 整数 A, B, C, D が空白区切りで標準入力に与えられる.
- 以下を繰り返す.
- 整数 e, f が空白区切りで標準入力に与えられる.
- e = f = 0 の場合,もぐらたたきを終了することを表す.プログラムを終了せよ.
- そうでない場合,もぐらがマス (e, f) に現れることを表す.標準出力に
1または2を 1 行で出力し,標準出力を flush せよ.1はくろうさを選ぶこと,2はしろうさを選ぶことを表す.
これに従わない入出力を行った場合のジャッジ結果は不定である (必ずしも WA になるとは限らない).
入出力例
| 入力 | 出力 | 説明 |
|---|---|---|
1 12 2 24 |
最初,くろうさがマス (1, 12) に,しろうさがマス (2, 24) にいる. | |
1 1 |
もぐらがマス (1, 1) に現れる. | |
2 |
しろうさを選んでいる.マス (2, 24) からマス (1, 1) へ動き,24 のコストがかかる. | |
2 100 |
もぐらがマス (2, 100) に現れる. | |
1 |
くろうさを選んでいる.マス (1, 12) からマス (2, 100) へ動き,89 のコストがかかる. | |
0 0 |
もぐらたたきを終了する.合計コストは 113 であり,z = 87 より 2 z + \lvert A - C \rvert + \lvert B - D \rvert = 187 なので,正解となる. |
実際のジャッジデータにおいて,この入出力例と一致する対話が生じ得るとは限らない.