A - Array Similarity

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

長さが等しい数列 a=(a_1,a_2,\dots,a_n) と b=(b_1,b_2,\dots,b_n) について、以下が成り立つとき、a と b は似ているといいます。

  • 任意の i=1,2,\dots,n について、a_i = \max(a_1,a_2,\dots,a_i) が成り立つとき、またそのときに限り、b_i = \max(b_1,b_2,\dots,b_i) が成り立つ。

数列 (A_1,A_2,\dots,A_N) が与えられます。Q 個のクエリに答えてください。クエリ i では整数 L_{i,1}, R_{i,1}, L_{i,2}, R_{i,2} が与えられるので、数列 (A_{L_{i,1}}, A_{L_{i,1} + 1}, \dots, A_{R_{i,1}}) と (A_{L_{i,2}}, A_{L_{i,2} + 1}, \dots, A_{R_{i,2}}) が似ているかどうか答えてください。

制約

  • 入力は全て整数
  • 1 \leq N \leq 2 \times 10^5
  • 1 \leq Q \leq 2 \times 10^5
  • 1 \leq A_i \leq 10^9
  • 1 \leq L_{i,1} \leq R_{i,1} \leq N
  • 1 \leq L_{i,2} \leq R_{i,2} \leq N
  • R_{i,1}-L_{i,1} = R_{i,2}-L_{i,2}

入力

入力は以下の形式で標準入力から与えられる。

N Q
A_1 A_2 \dots A_N
L_{1,1} R_{1,1} L_{1,2} R_{1,2}
L_{2,1} R_{2,1} L_{2,2} R_{2,2}
\vdots
L_{Q,1} R_{Q,1} L_{Q,2} R_{Q,2}

出力

Q 行出力せよ。i 行目には、数列 (A_{L_{i,1}}, A_{L_{i,1} + 1}, \dots, A_{R_{i,1}}) と (A_{L_{i,2}}, A_{L_{i,2} + 1}, \dots, A_{R_{i,2}}) が似ているなら Yes を、そうでないなら No を出力せよ。

入力例 1

10 6
3 1 4 1 5 9 2 6 5 3
1 3 3 5
1 5 6 10
1 1 9 9
1 9 1 9
1 3 6 8
5 8 7 10

出力例 1

Yes
No
Yes
Yes
No
Yes

1 つ目のクエリについて、(3,1,4) と (4,1,5) は似ています。したがって、Yes を出力します。

2 つ目のクエリについて、(3, 1, 4, 1, 5) と (9, 2, 6, 5, 3) は似ていません。したがって、No を出力します。

3 つ目のクエリについて、L_{i, 1} = R_{i, 1}, L_{i, 2} = R_{i, 2} を満たすクエリが与えられることがある点に注意してください。

4 つ目のクエリについて、L_{i, 1} = L_{i, 2}, R_{i, 1} = R_{i, 2} を満たすクエリも与えられることがある点に注意してください。
B - Bracket Character Frequency

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

(, ) のみからなる文字列 S について以下のいずれかの条件を満たすとき、かつそのときに限り S を正しい括弧列といいます。

  • S は空文字列である。
  • ある正しい括弧列 A が存在して、S は (, A, ) をこの順につなげた文字列である。
  • ある空でない正しい括弧列 A, B が存在して、S は A, B をこの順につなげた文字列である。

整数 N,K と長さ 2K の整数列 A=(A_1,A_2,\dots,A_{2K}) が与えられます。

以下の条件を満たす N 個の正しい括弧列の組が存在するか判定してください。

  • N 個の正しい括弧列の長さはいずれも 2K である。
  • 各 i=1, 2, \dots, 2K について、 N 個の正しい括弧列のうち、 i 文字目が ( であるものはちょうど A_i 個である。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

  • 入力は全て整数
  • 1 \leq T \leq 10^{5}
  • 1 \leq N \leq 10^{12}
  • 1 \leq K \leq 2\times 10^{5}
  • 0 \leq A_i \leq N
  • 1 つの入力に含まれるテストケースについて、K の総和は 5 \times 10^{5} 以下

入力

入力は以下の形式で標準入力から与えられる。

T
\mathrm{case_1}
\mathrm{case_2}
\vdots
\mathrm{case_T}

各ケースは以下の形式で与えられる。

N K
A_1 A_2 \ldots A_{2K}

出力

T 行出力せよ。i 行目には i 番目のテストケースについて、条件を満たす正しい括弧列の組が存在する場合は Yes を、 存在しない場合は No を出力せよ。

入力例 1

2
3 3
3 2 2 0 2 0
3 3
3 0 2 3 1 0

出力例 1

Yes
No

1 番目のテストケースについて、 ()()(), ((())), (())() の 3 つ組が条件を満たします。 2 番目のテストケースについて、条件を満たす正しい括弧列の組は存在しません。
C - Card Deck

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

1 から 10^{100} の番号がついた 10^{100} 枚のカードがあり、カード i が 上から i 番目になるように積まれています。 また、空の袋が 1 個あります。以下の操作をちょうど M 回行うことを考えます。

上から K 枚のカードを見て、カードを 0 枚以上好きな枚数選び、それらを袋に入れる。選ばれなかったカードは相対順序を保ったまま戻す。

操作終了後に袋に入っているカードの集合として考えられるもの全てに対する要素数の総和を 998244353 で割った余りを求めてください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

  • 入力は全て整数
  • 1 \leq T \leq 10^5
  • 1 \leq K <998244353
  • 1 \leq M < 998244353

入力

入力は以下の形式で標準入力から与えられる。

T
\mathrm{case}_1
\vdots
\mathrm{case}_T

各ケースは以下の形式で与えられる。

K\ M

出力

T 行出力せよ。i 行目には i 番目のテストケースに対する答えを出力せよ。

入力例 1

3
2 1
3 2
20250308 410338673

出力例 1

4
81
509595821

1 番目のテストケースについて、袋の中に入ったカードの集合としてありうるものは \lbrace \rbrace, \lbrace 1 \rbrace, \lbrace 2\rbrace, \lbrace 1,2 \rbrace で、要素数の総和は 4 です。
D - Digits of Prefix Product

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

この問題は output-only です。入力は与えられません。

以下の条件を全て満たす長さ 10 の正整数列 (a_1, a_2, \dots, a_{10}) を 1 つ出力してください。ただし、整数は先頭に 0 のない十進表記で考えるものとします。

  • a_1, a_2, \dots, a_{10} はそれぞれどの桁も 0 でない
  • a_1, a_2, \dots, a_{10} はそれぞれ 100 桁以上
  • a_1, a_2, \dots, a_{10} の桁数の和は 10^5 以下
  • 各 i (1 \le i \le 10) について、b_i = a_1 \times a_2 \times \dots \times a_i とするとき、b_i の隣り合う 2 桁は相異なる

入力

入力は与えられない。

出力

条件を満たす a_1, a_2, \dots, a_{10} を、（先頭に 0 のない十進表記で）この順に改行区切りで出力せよ。

出力例

28
19
2
19
15
3
14
14
29
27

(a_1, a_2, \dots, a_{10}) をこのように定めると、

  • b_1 = 28
  • b_2 = 532
  • b_3 = 1064
  • b_4 = 20216
  • b_5 = 303240
  • b_6 = 909720
  • b_7 = 12736080
  • b_8 = 178305120
  • b_9 = 5170848480
  • b_{10} = 139612908960

となるため、1, 3, 4 番目の条件を満たします。しかし 2 番目の条件を満たさないため、この出力は不正解と判定されます。
E - Edge Coloring Problem

Time Limit: 3 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

N 頂点 \frac{N(N-3)}{2} 辺からなる単純無向グラフが与えられます。グラフは 0,1 のみからなる N 個の文字列 S_1, S_2, \dots, S_{N} で表され、S_i の j 文字目が 1 の場合頂点 i, j を結ぶ辺が存在することを、 0 の場合存在しないことを表します。特に、S_i の i 文字目は必ず 0 です。

このグラフの各頂点の次数はいずれも N-3 です。

これからグラフの各辺に 1 以上の整数を割り当てることを考えます。このとき、共通の頂点を端点にもつどの 2 辺についても互いに相異なる整数が割り当てられているような割当を辺彩色といい、辺彩色に用いられる整数の最大値として考えられる値の最小値を辺彩色数といいます。

グラフの辺彩色数を求め、実際にそれを達成する辺彩色を 1 つ求めてください。

制約

  • 4 \leq N \leq 300
  • S_1,S_2,\dots,S_N は 0,1 のみからなる長さ N の文字列
  • 与えられるグラフは各頂点の次数が N-3 であるような単純無向グラフ

入力

入力は以下の形式で標準入力から与えられる。

N
S_1
S_2
\vdots
S_{N}

出力

辺彩色数 C と頂点 i,j を結ぶ辺に割り当てる整数 c_{i,j} について、以下の形式で出力せよ。

C
c_{1,1} c_{1,2} \dots c_{1,N}
c_{2,1} c_{2,2} \dots c_{2,N}
\vdots
c_{N,1} c_{N,2} \dots c_{N,N}

ただし、頂点 i,j を結ぶ辺が存在しないような i,j に対しては c_{i,j}=-1 として出力せよ。とくに c_{i,i} については c_{i,i}=-1 として出力せよ。

条件を満たす出力が複数存在する場合、いずれの出力も正当とみなされる。

入力例 1

6
011100
101010
110001
100011
010101
001110

出力例 1

3
-1 2 3 1 -1 -1
2 -1 1 -1 3 -1
3 1 -1 -1 -1 2
1 -1 -1 -1 2 3
-1 3 -1 2 -1 1
-1 -1 2 3 1 -1

頂点 1 は頂点 2,3,4 と結ばれており、これらの辺には互いに相異なる整数を割り当てなければならないので、辺彩色数は 3 以上です。

出力のように整数を割り当てると、例えば頂点 1 と頂点 2,3,4 を結ぶ辺にはそれぞれ整数 2,3,1 が割り当てられており、互いに相異なります。他の頂点 v についても同様に v を端点とする辺には互いに相異なる整数が割り当てられていることが確認できます。よって出力は辺彩色になっており、辺彩色数は 3 であるとわかります。

入力例 2

5
01001
10100
01010
00101
10010

出力例 2

3
-1 2 -1 -1 1
2 -1 3 -1 -1
-1 3 -1 1 -1
-1 -1 1 -1 3
1 -1 -1 3 -1
F - Fourier Coefficients

Time Limit: 8 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

この問題はインタラクティブな問題（あなたの作成したプログラムとジャッジプログラムが標準入出力を介して対話を行う形式の問題）です。ジャッジプログラムの実行は最大で 1.3 秒程度を要します。

整数 N が与えられます。ジャッジプログラムは関数 f(x) \coloneqq \sum_{k=0}^{N-1} A_k \cos{kx} を隠し持っています。ここで、A_0, \dots, A_{N - 1} は 0 以上 998244353 未満の整数です。

以下の対話により、整数 A_0, \dots, A_{N - 1} を特定してください。

  • あなたは N 個の整数組 (X_1, Y_1), \dots, (X_N, Y_N) を出力する。各整数組 (X_i, Y_i) は 0 \le X_i \le Y_i < 998244353 および Y_i \neq 0 を満たす必要がある。
  • ジャッジプログラムは N 個の整数 Z_1, \dots, Z_N を返答する。各整数 Z_i は Z_i \coloneqq f(\arccos(X_i / Y_i)) \bmod 998244353 と定められる。
Z_i の厳密な定義 X_i, Y_i の制約下で、f(\arccos(X_i / Y_i)) が有理数になり、特に既約分数 P_i / Q_i と表したときに Q_i \not\equiv 0 \pmod{998244353} となることが示せます。 このとき Z_i を、0 以上 998244353 未満の整数であって、Z_i Q_i \equiv P_i \pmod{998244353} を満たす整数として定義します。なお、このような Z_i は常に存在して一意であることが示せます。

制約

  • 入力は全て整数
  • 1 \leq N \leq 5 \times 10^{5}

入出力

この問題はインタラクティブな問題（あなたの作成したプログラムとジャッジプログラムが標準入出力を介して対話を行う形式の問題）です。

最初に、N を標準入力から受け取ってください。

N

その後、条件を満たすような (X_1, Y_1), \dots, (X_N, Y_N) を標準出力に以下の形式で出力してください。

X_1 Y_1
X_2 Y_2
\vdots
X_N Y_N

出力が正当な場合、返答が以下の形式で標準入力から与えられます。

Z_1
Z_2
\vdots
Z_N

出力が不正な場合、返答の代わりに -1 が与えられます。

-1

-1 が入力に与えられた場合、直ちにプログラムを終了してください。

その後、答えを標準出力に以下の形式で出力してください。

A_0
A_1
\vdots
A_{N-1}

注意点

  • 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
  • 対話の途中で不正な出力を行った、あるいはプログラムが途中で終了した場合のジャッジ結果は不定です。
  • 答えを出力したら（または -1 を受け取ったら）直ちにプログラムを正常終了してください。そうしなかった場合、ジャッジ結果は不定です。
  • 特に、余計な改行も不正なフォーマットの出力とみなされるので注意してください。
  • ジャッジは適応的ではありません。つまり、整数 A_0, \dots, A_{N - 1} は対話の開始時に固定され、対話の途中で変更されることはありません。

入出力例

以下は N = 2 および (A_0, A_1) = (3, 2) の場合の入出力例です。

入力 出力 説明
2 N が与えられます。
0 1
1 1		 条件を満たす (X_i, Y_i) をクエリします。
3
5 		f(\arccos(X_i / Y_i)) の値が返答として与えられます。
3
2 		答えである (A_0, A_1) = (3, 2) を出力します。
G - Guarding Plan

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

2 次元座標平面上に N 人の警備員が立っています。i 人目の警備員は点 (x_i, y_i) に立っています。あなたは次の操作を 0 回以上好きな回数繰り返すことができます。

  • 警備員の立っている点を 2 つ選び、その 2 点を端点とする線分上の点を 1 つ選ぶ。その点に警備員が立っていない場合、そこに新しく警備員を立たせる。

点 (a, b) に立っている警備員は、x 座標が a 以下かつ y 座標が b 以下の領域にいる警備員を監視します。自分以外の警備員に監視されていない警備員を「必要な警備員」と呼びます。

最終的な警備員の配置における「必要な警備員」の人数の最小値を求めてください。さらに、「必要な警備員」の人数を最小にするために必要な操作回数の最小値を求めてください。

制約

  • 入力は全て整数
  • 1 \leq N \leq 2\times 10^5
  • 0 \leq x_i, y_i \leq 10^9 (1\leq i\leq N)
  • (x_i, y_i)\neq (x_j, y_j) (i\neq j)

入力

入力は以下の形式で標準入力から与えられる。

N
x_1 y_1
\vdots
x_N y_N

出力

2 行にわたり出力せよ。1 行目には、達成できる「必要な警備員」の人数の最小値を出力せよ。2 行目には、その最小値を達成するために必要な操作回数の最小値を出力せよ。

入力例 1

5
1 6
2 4
3 3
4 2
6 1

出力例 1

4
1

点 (1,6) と点 (6,1) の警備員の間の点 (3,4) を選び、ここに新たに警備員を立たせます。この操作の後で、「必要な警備員」は (1,6),(3,4),(4,2),(6,1) に立っている 4 人になります。

入力例 2

3
0 0
1 2
2 1

出力例 2

2
0

入力例 3

7
10 49
9 27
59 8
19 22
0 50
25 23
33 13

出力例 3

4
1
H - Hidden Sequence Rotation

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

この問題はインタラクティブな問題（あなたの作成したプログラムとジャッジプログラムが標準入出力を介して対話を行う形式の問題）です。

整数 N が与えられます。ジャッジは 1 以上 10^5 以下の整数からなる長さ N の数列 A = (A_{0}, \dots, A_{N-1}) を隠し持っています。以降を含め、添え字が 0 から始まっていることに注意してください。

整数 s = 0, \dots, N-1 および l = 1, \dots, N に対し、数列 A(s, l) を以下のように定義します。

  • 長さ l の数列であって、i=0,\dots,l-1 番目の要素がそれぞれ A_{(s+i) \bmod N} であるようなもの

あなたはジャッジに以下の形式の質問を 20 回まで行うことができます。

  • あなたは整数の組からなる列 ((s_0,l_0),\dots,(s_{k-1},l_{k-1})) であって以下の制約を満たすものを出力する。
    • 1 \le k \le N
    • 0 \le s_i < N
    • 1 \le l_i \le N
    • \sum_{i = 0}^{k - 1} l_i \leq N
  • それに対しジャッジは i = 0, \dots, k - 1 の中で A(s_i, l_i) が辞書順最小を与えるような i を全て返答する。つまり、A_{\mathrm{tmpmin}} = \min_{0 \le i < k} A(s_i, l_i) としたとき、集合 \lbrace i_0, \dots, i_{k'-1} \rbrace \coloneqq \lbrace i \mid 0 \le i < k, \, A(s_i,l_i) = A_{\mathrm{tmpmin}} \rbrace を返答する。

上記の質問により、s = 0, \dots, N - 1 の中で A(s, N) が辞書順最小を与えるような s を全て特定してください。つまり、A_{\mathrm{min}} = \min_{0 \leq s < N} A(s,N) としたとき、集合 \lbrace s_0, \dots, s_{n-1} \rbrace \coloneqq \lbrace s \mid 0 \le s < N, \, A(s, N) = A_{\mathrm{min}} \rbrace を特定してください。

制約

  • 入力は全て整数
  • 1 \leq N \leq 10^{5}

入出力

この問題はインタラクティブな問題（あなたの作成したプログラムとジャッジプログラムが標準入出力を介して対話を行う形式の問題）です。

最初に、N を標準入力から受け取ってください。

N

その後、あなたは質問を行うことができます。質問は標準出力に以下の形式で出力してください。

? k
s_0 l_0
s_1 l_1
\vdots
s_{k-1} l_{k-1}

ここで、出力は問題文に記載された質問の条件を満たす必要があります。

質問が正当な場合、その質問への答えが以下の形式で標準入力から与えられます。

k'
i_0
i_1
\vdots
i_{k'-1}

ここで、入力は 0 \le i_0 < \dots < i_{k'-1} < k という条件を満たします。

質問の形式が間違っている、質問を規定の回数より多く行った、などの理由から質問が不正と判定された場合、質問への答えの代わりに -1 が与えられます。

-1

-1 が入力に与えられた場合、ただちにプログラムを終了してください。

答えが分かったら、標準出力に以下の形式で出力してください。

! n
s_0
s_1
\vdots
s_{n-1}

ここで、s_i は 0 以上 N 未満の相異なる整数である必要があります。

注意点

  • 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
  • 対話の途中で不正な出力を行った、あるいはプログラムが途中で終了した場合のジャッジ結果は不定です。
  • 答えを出力したら（または -1 を受け取ったら）直ちにプログラムを正常終了してください。そうしなかった場合、ジャッジ結果は不定です。
  • 特に、余計な改行も不正なフォーマットの出力とみなされるので注意してください。
  • ジャッジは適応的ではありません。つまり、数列 A は対話の開始時に固定され、対話の途中で変更されることはありません。

入出力例

以下は N = 6, A=(1, 2, 3, 1, 2, 4) の場合の入出力例です。

入力 出力 説明
6 N が与えられます。
? 3
0 1
1 1
3 1		 A(0, 1) = (1), A(1, 1) = (2), A(3, 1) = (1) をクエリします。
2
0
2 		0 番目、2 番目の数列が辞書順最小です。
? 2
0 3
3 3		 A(0, 3) = (1, 2, 3), A(3, 3) = (1, 2, 4) をクエリします。
1
0 		0 番目の数列が辞書順最小です。
! 1
0 		A(s, N) が辞書順最小となる s は 0 のみなので、それを答えとして出力します。
I - Insert AB or BA

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

A と B からなる文字列 S と T が与えられます。

以下の 2 種類の操作を、0 回以上の好きな回数、好きな順番で行うことを考えます。

  • S の任意の位置に AB を挿入する。コストが X かかる。
  • S の任意の位置に BA を挿入する。コストが Y かかる。

なお、挿入は先頭・末尾に対して行うこともできます。

S を T と一致させることが可能かを判定し、可能な場合は必要な合計コストの最小値を求めてください。

制約

  • X, Y は整数
  • S, T は A と B からなる文字列
  • 1 \le |S| \le |T| \le 8000
  • 1 \le X \le 10^9
  • 1 \le Y \le 10^9

入力

入力は以下の形式で標準入力から与えられる。

S T
X Y

出力

S を T と一致させることが可能な場合は、必要な合計コストの最小値を 1 行に出力せよ。不可能な場合は -1 を出力せよ。

入力例 1

AB ABAABB
5 3

出力例 1

8

はじめ、S = AB です。以下のように操作を行うことで、S を T= ABAABB に一致させることができます。

  • S = AB の 1 文字目と 2 文字目の間に BA を挿入する。S = ABAB となる。
  • S = ABAB の 3 文字目と 4 文字目の間に AB を挿入する。S = ABAABB となる。

この場合、かかるコストの合計は 3 + 5 = 8 となります。実はこれが必要な合計コストの最小値でもあります。

入力例 2

AAAAAA AAAAAA
2 3

出力例 2

0

入力例 3

AAAAA BBBBBBB
9982 44353

出力例 3

-1

入力例 4

AAABBABABBBBBBABBABBA AAABABBABABBABBBBBABBBBBAAAAABBABABBAABBA
1 100000

出力例 4

300007
J - Journey through the Fractal

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

1 辺の長さが 2^{i-1} の正三角形を、レベル i の三角形と呼びます。また、次の規則にしたがって生成される図形を、レベル i のフラクタルと呼びます。

  • レベル 1 のフラクタルは、レベル 1 の三角形である
  • レベル i + 1 (i \geq 1) のフラクタルは、レベル i の三角形の 3 辺のそれぞれにぴったり接するように、レベル i のフラクタルを配置した図形である（詳しくは、図を参照してください）

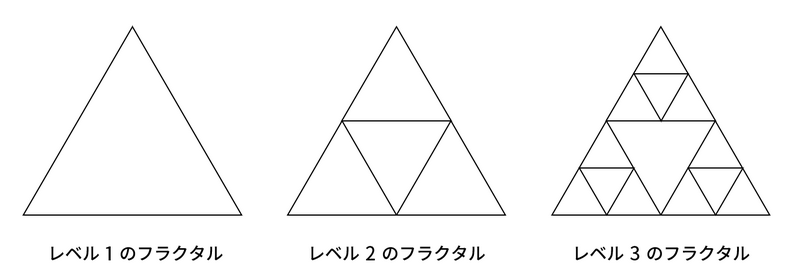
ここに、レベル L のフラクタルがあります。

Alice は、まず初めに、フラクタルを構成する三角形のうち好きなものを 1 つ選び、その三角形からスタートします。その後、まだ訪れていない三角形であって、今いる三角形に辺で隣接するものがあれば 1 つ選び、移動します。

Alice は移動を K 回まで行うことができます。Alice が訪れた三角形（スタートした三角形も含む）のレベルの総和を、スコアと定めます。

スコアとしてありうる値の最大値を 998244353 で割った余りを求めてください。なお、998244353 で割った余りの最大値を求めるのではないことに注意してください。

制約

  • 入力は全て整数
  • 1 \leq L \leq 10^9
  • 1 \leq K \leq 10^{18}

入力

入力は以下の形式で標準入力から与えられる。

L K

出力

スコアの最大値を 998244353 で割った余りを出力せよ。

入力例 1

3 4

出力例 1

6

図のように移動することで、レベル 1 の三角形を 4 つ、レベル 2 の三角形を 1 つ訪れることができます。

なお、図の三角形の中に書かれている数は、その三角形を何番目に訪れたかを表します。

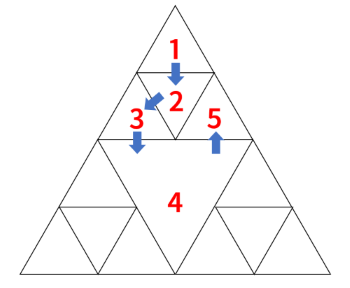
入力例 2

998244353 100000000000000007

出力例 2

756221200

スコアの最大値を 998244353 で割った余りを出力してください。
K - K-rep Array

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

正整数 K について、正整数からなる数列 V が K-rep であるとは以下の条件を満たすこととします。

  • 正整数からなる長さ K の数列 B が存在して、B を 10^{100} 回繰り返した数列 B' が連続部分列として V を含む。

各要素が正整数または -1 である、長さ N の数列 A = (A_1, A_2, \ldots, A_N) が与えられます。K = 1, 2, \ldots, N について、以下の問題を解いてください。

正整数からなる長さ N の数列 V = ( V_1, V_2, \dots, V_N ) であって、A_i \neq -1 ならば V_i = A_i を満たすもののうち、K-rep であるものが存在するか判定してください。

制約

  • 入力は全て整数
  • 1 \leq N \leq 2\times 10^5
  • 1 \leq A_i \leq N または A_i = -1

入力

入力は以下の形式で標準入力から与えられる。

N
A_1 \ A_2 \ \dots \ A_N

出力

長さ N の文字列を出力せよ。i 文字目は K = i とした場合の問題について、条件を満たす数列が存在するとき 1 と、存在しないとき 0 とせよ。

入力例 1

5
1 2 -1 2 1

出力例 1

01011

正整数からなる長さ N の数列 V = ( V_1, V_2, \dots, V_N ) であって、A_i \neq -1 ならば V_i = A_i を満たすものの 1 つとして V = (1, 2, 3, 2, 1) があります。K = 4 について、B = (2, 3, 2, 1) とすると B' は連続部分列として (1, 2, 3, 2, 1) を含むため (1, 2, 3, 2, 1) は K-rep です。
L - LIS Triangle

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

正整数 N,K,L が与えられます。次の条件を全て満たす長さ N の整数列 P が存在するか判定し、存在する場合は 1 つ示してください。

  • P は整数列 (K, K + 1, \dots, K + N - 1) の順列
  • P の最長増加部分列の長さは L
  • 1 \leq i \leq N - 2 を満たす i に対して、P_i, P_{i+1}, P_{i+2} を 3 辺の長さとする（非退化な）三角形が存在する

T 個のテストケースが与えられるので、それぞれについて答えてください。

最長増加部分列とは 数列 P の部分列とは、P の要素をいくつか抜き出して元の順に並べてできる列のことを指します。 数列 P の最長増加部分列とは、P の狭義単調増加な部分列であって、長さが最大のものを指します。
非退化な三角形とは 非退化な三角形とは、3 つの頂点が同一直線上に並ばないような三角形のことを指します。

制約

  • 入力は全て整数
  • 1 \leq T \leq 50000
  • 3 \leq N \leq 2 \times 10^5
  • 1 \leq K \leq 2 \times 10^5
  • 1 \leq L \leq N
  • 1 つの入力に含まれるテストケースについて、N の総和は 2 \times 10^5 以下

入力

入力は以下の形式で標準入力から与えられる。

T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T

各ケースは以下の形式で与えられる。

N K L

出力

各テストケースに対する答えを順に改行区切りで出力せよ。

あるテストケースについて、条件を全て満たす P が存在しない場合は No を出力せよ。存在する場合は、条件を全て満たす整数列 P のうち 1 つを、以下の形式で出力せよ。条件を全て満たす整数列 P が複数存在する場合は、いずれを出力しても正解となる。

Yes
P_1 P_2 \dots P_N

入力例 1

3
6 3 4
5 5 5
7 1 2

出力例 1

Yes
3 6 4 7 5 8
Yes
5 6 7 8 9
No

1 つ目のテストケースについて、条件を満たす整数列の 1 つに、P=(3, 6, 4, 7, 5, 8) があります。条件を満たす整数列は他にも存在します。

2 つ目のテストケースについて、P=(5, 6, 7, 8, 9) が条件を満たす唯一の整数列です。

3 つ目のテストケースについて、条件を満たす整数列 P は存在しません。
M - Minimum Distance Tree

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

頂点に 1 から N の番号がついた N 頂点 M 辺からなる重み付き単純連結無向グラフ G があります。 i 番目の辺は頂点 u_i,v_i を結ぶ重み w_i の辺です。

頂点に 1 から N の番号がついた N 頂点の重み付き木 T であって、任意の 2 頂点 u,v に対し、 G 上の u-v 最短経路長が T 上の u-v 最短経路長に等しいようなものが存在するか判定してください。

制約

  • 入力は全て整数
  • 2 \leq N \leq 5 \times 10^5
  • N-1 \leq M \leq 5 \times 10^5
  • 1 \leq u_i, v_i \leq N
  • 1 \leq w_i \leq 10^9
  • 与えられるグラフは単純かつ連結

入力

入力は以下の形式で標準入力から与えられる。

N M
u_1 v_1 w_1
u_2 v_2 w_2
\vdots
u_M v_M w_M

出力

上記のような T が存在する場合は Yes を、存在しない場合は No を出力せよ。

入力例 1

3 3
1 2 3
2 3 4
3 1 100

出力例 1

Yes

T として、頂点 1,2 間に重み 3 の辺、頂点 2,3 間に重み 4 の辺がある 3 頂点の木が条件を満たします。

入力例 2

3 3
1 2 3
2 3 4
3 1 2

出力例 2

No

条件を満たす T は存在しません。例えば、頂点 1,2 間に重み 2 の辺、頂点 1,3 間に重み 2 の辺がある 3 頂点の木は、G 上での 1-2 最短経路長が 3 であるのに対して、この木上での 1-2 最短経路長が 2 であり等しくないため条件を満たしません。
N - Nice Bouquets

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

花の販売を行う Universal Tropical Plant Center (UTPC) 社が所有する農園は、東西に一列に N 本の木が植えられており、西から順に 1,2,\dots,N の番号が付いています。

UTPC 社の農園ではこれから、K 日間の収穫期に入ります。収穫期の間、それぞれの木は毎日、赤、緑、青のいずれかの色の花を 1 つだけ咲かせます。木 i が今後 K 日間で咲かせる花の色の情報は文字列 S_i で表され、j 日目に咲かせる花の色について、S_i の j 文字目 S_{i,j} が R の場合は赤色、 G の場合は緑色、 B の場合は青色であることを表します。

UTPC 社では毎日、その日に咲いた全ての花を収穫し、3 つずつ花束にして販売します。この花束は必ず、3 つの花が全て同じ色か、全て異なる色になるようにします。 本来は、毎日収穫した花が 1 つも余らないように花束を作りたいのですが、現状ではこのような花束の作り方が存在するとは限りません。そこで、収穫期に入る前に、次の操作をそれぞれ好きな回数繰り返すことにしました。

  • 1 以上 N 以下の整数 i を選び、木 i を切る。切った木からは花が収穫できなくなる。
  • 1 以上 N 以下の整数 i を選び、木 i に促進剤をかける。促進剤をかけると、今後 K 日間は 2 つの花を咲かせるようになる。つまり、j 日目には S_{i,j} の色の花を 2 つ咲かせることになる。

なお、同じ木に対して 2 回以上操作を行うことはできません。また、この操作は収穫期に入った後に行うことはできません。

UTPC 社の事務所は農園の西端にあるので、東に植えられている木に対してはなるべく操作を行いたくないです。そこで、一連の操作のコストを、操作した木のうち最も東側にあるものの番号によって定義します。どの木に対しても操作を行わない場合のコストは 0 とします。

収穫期の間どの日も花が 1 つも余らなくなるような操作方法の中での、コストの最小値を求めてください。なお、全ての木を切った場合、花は 1 つも余らないと考えるものとします。

制約

  • N, K は整数
  • 1 \leq N,K
  • NK \leq 10^5
  • |S_i|=K
  • S_i の各文字は R, G, B のいずれかである

入力

入力は以下の形式で標準入力から与えられる。

N K
S_1
S_2
\vdots
S_N

出力

答えを 1 行に出力せよ。

入力例 1

4 5
RGBGR
BGGBR
RBGBR
RRRRR

出力例 1

2

2 番目の木を切ると、咲く花の色は

  • 1 日目：RRR
  • 2 日目：GBR
  • 3 日目：BGR
  • 4 日目：GBR
  • 5 日目：RRR

となり、どの日も条件を満たします。この場合のコストは 2 です。コスト 1 で目標を達成することはできません。

入力例 2

3 3
RGB
BGG
GGR

出力例 2

0

操作を行う必要はありません。

入力例 3

3 4
GGGG
BGGG
GGGR

出力例 3

3

全ての木を切る必要があります。

入力例 4

6 4
BGGB
BGGB
RGBG
RRRR
GGGG
BBBB

出力例 4

3

1 番目の木に促進剤をかけ、3 番目の木を切ると、咲く花の色は

  • 1 日目：BBBRGB
  • 2 日目：GGGRGB
  • 3 日目：GGGRGB
  • 4 日目：BBBRGB

となり、どの日も条件を満たします。
O - One Different Inequality

Time Limit: 3 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

整数 N と、< または > からなる長さ N-1 の文字列 S が与えられます。

(1,2,\dots,N) の順列 P=(P_1,P_2,\dots,P_N) を考えます。

P が以下の条件を満たすとき、P は良い順列であるといいます。

  • 全ての i\ (1 \leq i \leq N-1) について、S の i 文字目が < ならば P_i < P_{i+1} 、> ならば P_i > P_{i+1} が成り立つ。

また、P が以下の条件をすべて満たすとき、P は素晴らしい順列であるといいます。

  • P は良い順列である。
  • |P_i-P_{i+1}|=1 を満たす i\ (1 \leq i \leq N-1) の個数が良い順列の中で最大である。

素晴らしい順列の個数を 998244353 で割った余りを求めてください。

制約

  • N は整数
  • 2 \leq N \leq 2 \times 10^5
  • S は < または > からなる長さ N-1 の文字列

部分点

  • 追加の制約 2 \leq N \leq 10000 を満たすデータセットに正解した場合は 20 点が与えられる。

入力

入力は以下の形式で標準入力から与えられる。

N
S

出力

答えを 1 行に出力せよ。

入力例 1

5
<<>>

出力例 1

2

良い順列の例としては (1,2,5,4,3) や (2,3,5,4,1) があげられます。|P_i-P_{i+1}|=1 を満たす i の個数はそれぞれ 3,2 個です。

良い順列における |P_i-P_{i+1}|=1 を満たす i の個数の最大値は 3 個であることが証明でき、素晴らしい順列は (1,2,5,4,3) と (3,4,5,2,1) の 2 つになります。

入力例 2

40
<<>><>><>>>><><<><><><<>><<<<>><><<<>><

出力例 2

535474657
P - Perfect Suika Game on a Tree

Time Limit: 5 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

1 から N までの番号が付いた N 頂点からなる木 T があります。 i 番目の辺は頂点 u_i,v_i を結びます。

各頂点にはレベルと呼ばれる正整数が割り当てられています。はじめ、各頂点 v = 1,2,\dots,N のレベルは A_v です。

木 T について、以下の問題を考えます。

木 T に対し以下のような操作をちょうど N-1 回行うことで、 T を 1 頂点のみからなる木にすることができるか判定してください。
  • 両端点の頂点のレベルが等しいような辺を 1 つ選び、選んだ辺について縮約を行う。両端点の頂点のレベルを l としたとき、縮約により生じる新たな頂点のレベルを l+1 とする。

クエリが Q 個与えられるので処理してください。 i 番目のクエリでは辺番号 e_i が与えられるので、木 T における頂点 u_{e_i},v_{e_i} のレベルをスワップした後（このスワップの影響は以降のクエリにも残存します）、上記の問題の答えを出力してください。

制約

  • 入力はすべて整数
  • 2 \leq N \leq 2 \times 10^5
  • 1 \leq u_i,v_i \leq N
  • 1 \leq A_i \leq N
  • 1 \leq Q \leq 2 \times 10^5
  • 1 \leq e_i \leq N-1
  • 与えられるグラフは木

部分点

  • 追加の制約 Q=1 を満たすデータセットに正解した場合は 20 点が与えられる。

なお、以下で与えられるサンプルケースはいずれも部分点のデータセットに含まれない。

入力

入力は以下の形式で標準入力から与えられる。

N 
u_1 v_1
u_2 v_2
\vdots
u_{N-1} v_{N-1}
A_1 A_2 \dots A_N
Q
e_1
e_2
\vdots
e_Q

出力

Q 行出力せよ。 i 行目には i 番目のクエリについてレベルのスワップを行った後、上記の問題について、T を 1 頂点のみからなる木にすることができる場合 Yes を、できない場合 No を出力せよ。

入力例 1

4
1 2
1 3
1 4
1 1 2 3
4
1
2
3
1

出力例 1

Yes
No
No
Yes

1 番目のクエリについて、頂点 u_1=1, v_1=2 のレベルのスワップを行った後、頂点 1,2,3,4 のレベルはそれぞれ 1,1,2,3 になります。

この場合、下図のように赤く表示されている辺を選んで操作を行うことで、レベル 4 の頂点 1 つからなる木にできます（下図において頂点に書かれている整数は頂点のレベルを示しています）。

縮約操作の例

よって 1 行目には Yes を出力します。

2 番目のクエリについて、頂点 u_2=1, v_2=3 のレベルのスワップを行った後、頂点 1,2,3,4 のレベルはそれぞれ 2,1,1,3 になります。

この場合、操作を 1 度も行うことができず、 1 つの頂点からなる木に変換することはできません。

よって 2 行目には No を出力します。

入力例 2

15
1 2
1 3
2 4
1 5
1 6
4 7
1 8
7 9
2 10
2 11
2 12
11 13
11 14
2 15
2 3 13 4 8 10 7 9 11 12 1 1 6 14 5
1
11

出力例 2

Yes

入力例 3

20
1 2
1 3
2 4
1 5
2 6
5 7
4 8
3 9
6 10
7 11
11 12
12 13
13 14
14 15
15 16
16 17
17 18
18 19
19 20
4 4 7 3 8 2 8 6 4 2 3 3 4 5 6 5 4 3 3 6
10
8
19
5
9
19
10
19
19
10
19

出力例 3

No
No
No
No
Yes
No
No
No
Yes
No
Q - Quadratic Pieces

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 100 点

問題文

長さ N の整数列 A = (A_1, A_2, \dots, A_N) が与えられます。

1 \le L \le R \le N を満たす整数 L, R によって定まる連続部分列 (A_L, A_{L + 1}, \dots, A_R) が以下の条件を満たすとき、その連続部分列は 2 次関数的であると定めます。

  • ある実数 a, b, c が存在し、L \le i \le R を満たす任意の整数 i が A_i = a i^2 + b i + c を満たす。

整数列 A をいくつかの 2 次関数的な連続部分列に分割することを考えます。分割後の連続部分列の個数としてありうる値のうち最小値を出力してください。

T 個のテストケースが与えられるので、それぞれについて答えてください。

制約

  • 入力は全て整数
  • 1 \le T \le 10^5
  • 1 \le N \le 2 \times 10^5
  • -10^{18} \le A_i \le 10^{18}
  • 1 つの入力に含まれるテストケースについて、N の総和は 2 \times 10^5 以下

入力

入力は以下の形式で標準入力から与えられる。

T
\mathrm{case}_1
\mathrm{case}_2
\vdots
\mathrm{case}_T

各ケースは以下の形式で与えられる。

N
A_1 A_2 \ldots A_N

出力

T 行出力せよ。i 行目には i 番目のテストケースに対する答えを出力せよ。

入力例 1

4
12
-16 -9 -4 -1 0 0 0 0 1 4 9 16
8
2 0 2 5 0 3 0 8
1
0
5
1000000000000000000 -500000000000000000 -1000000000000000000 -500000000000000000 1000000000000000000

出力例 1

3
3
1
1

1 つ目のテストケースについて、与えられた整数列は 3 つの 2 次関数的な連続部分列 (-16, -9, -4, -1), \,(0, 0, 0),\, (0, 1, 4, 9, 16) に分割できます。 実際、それぞれの連続部分列について、(a, b, c) = (-1, 10, -25), \, (0, 0, 0),\, (1, -16, 64) が条件を満たしていることがわかります。 2 つ以下の 2 次関数的な連続部分列に分割することはできないので、答えは 3 となります。

4 つ目のテストケースについて、入力値が 32 bit 整数型に収まらない場合があることに注意してください。