Time Limit: 1 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国の王様は,Unagi The synthesis Programming Contest(略称: UTPC)というコンテストを開催しようとしている.そこで,UTPCのかっこいいロゴを募集したのだが,王様はとても目が悪いので,アルファベットの穴の数の違いでしか文字列を区別できない.
課題
大文字アルファベットからなる長さ4の文字列 s が与えられる. s が文字列 "UTPC" と「穴の数の意味で等しい」かを答えよ.「穴の数の意味で等しい」とは,対応する各位置の2文字のアルファベットの穴の数が等しいことを意味する.ここで,穴の数が0個のアルファベットは CEFGHIJKLMNSTUVWXYZ であり,穴の数が1個のアルファベットは ADOPQR であり,穴の数が2個のアルファベットは B である.
配点
100
入力
入力は以下の形式で与えられる.
s1s2s3s4
s_iはそれぞれi番目の文字を表している.
制約
入力中の各変数は以下の制約を満たす.
- 各 si は 'A' から 'Z' のアルファベット1文字である
出力
与えられた文字列が文字列 "UTPC" と等しければ "yes" ,等しくなければ "no" を1行に出力せよ.
入力例1
KUPC
入力例1に対する出力例
yes
実は KUPC=UTPC だったのである.
入力例2
UTPC
入力例2に対する出力例
yes
入力例3
UTBC
入力例3に対する出力例
no
B には穴が2つあることに注意せよ.
Time Limit: 1 sec / Memory Limit: 256 MB
問題
背景
西暦2013年12月,うなぎ王国の王様は困っていた.年末までに片付けなければならない仕事が山ほど溜まっていたからである.このままでは年内に Unagi The synthesis Programming Contest(略称: UTPC)が開催できず部下たちに怒られてしまう.そこで,王様は新しい暦「うなぎ暦」を作って年末を先延ばしにしようと考えた.しかし,単に1年を13ヶ月にするだけでは翌年の年末にまた苦労することは目に見えている.そこで,王様は毎年1ヶ月ずつ月を増やすことにした.
課題
西暦の年月が与えられるので,対応するうなぎ暦での年月を答えよ.うなぎ暦の詳細は以下のとおりである.
うなぎ暦は西暦2013年12月から施行され,西暦2013年12月はうなぎ暦2013年12月に対応する.うなぎ暦では年によって月の数が異なり,うなぎ暦 Y 年は (Y−2000) ヶ月からなる.例えばうなぎ暦2013年には13月まで存在し,うなぎ暦2014年には14月まで存在する.西暦において月が変わると同時に,うなぎ暦でも月が変わるとする.つまり,うなぎ暦のある月の途中に西暦の月が変わったり,西暦のある月の途中にうなぎ暦が変わったりすることはない.以下の表に,西暦とうなぎ暦の対応の例を示す.
| 西暦 | 2013年12月 | 2014年1月 | 2014年2月 | ... | 2014年12月 | 2015年1月 | ... | 2015年3月 | 2015年4月 |
| うなぎ暦 | 2013年12月 | 2013年13月 | 2014年1月 | ... | 2014年11月 | 2014年12月 | ... | 2014年14月 | 2015年1月 |
配点
100
入力
入力は以下の形式で与えられる.
Y M
Y,M はそれぞれ西暦での年,月を表す整数である.
制約
入力中の各変数は以下の制約を満たす.
- 2013 \leq Y \leq 1017
- 1 \leq M \leq 12
- 西暦2013年12月以降の年月が与えられる
部分点
この問題には部分点が設定されている.この問題のテストケースのうち50点分は,追加で以下の制約も満たす.
- 1 \leq Y \leq 105
出力
うなぎ暦における年と月をスペース区切りで1行に出力せよ.
入力例1
2013 12
入力例1に対する出力例
2013 12
西暦2013年12月にうなぎ暦が施行された.
入力例2
2014 1
入力例2に対する出力例
2013 13
うなぎ暦2013年には13月まで存在する.
入力例3
12345 6
入力例3に対する出力例
2498 315
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国の隣にはうさぎ王国がある.各王国には沢山の都市があり,都市間には道路がひかれている.現在,うなぎ王国とうさぎ王国を行き来する道路は存在しない.そこで,うなぎ王国の王様はうさぎ王国と友好関係を築くため,2つの王国の都市間に道路を1本建設しようと考えている.建設候補となる道路は沢山あるため,運送コストに敏感な王様は都市間の最短距離の最大値がどのような値をとるかを知りたがっている.
課題
頂点数 n1,辺数 m1 の無向グラフ G1 と頂点数 n2,辺数 m2 の無向グラフ G2 が与えられる.各々のグラフは連結である.すなわち,各グラフについて,任意の2頂点を結ぶ経路が存在する.あなたは,1本の辺を追加して2つのグラフを連結にしようと思っている.辺はどのように追加しても構わない.出来上がるグラフ上で最も遠い2点間の距離(グラフの直径と呼ばれる)が最小・最大いくつになるか答えよ.
配点
100
入力
入力は以下の形式で与えられる.
n1 m1 a1 b1 a2 b2 ... am1 bm1 n2 m2 c1 d1 c2 d2 ... cm2 dm2
最初の行にはグラフ G1 の頂点数 n1 と辺数 m1 が与えられる.続く m1 行には辺の情報が与えられる. ai,bi は G1 において2頂点 ai,bi 間に辺があること意味する.次の行にはグラフ G2 の頂点数 n2 と辺数 m2 が与えられる.続く m2 行には辺の情報が与えられる. ci,di は G2 において2頂点 ci,di 間に辺があること意味する.
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq n1,n2 \leq 1000 (=103)
- 0 \leq m1,m2 \leq 10000 (=104)
- 0 \leq ai,bi \lt n1
- 0 \leq ci,di \lt n2
- 各グラフは連結である
- 各グラフは単純である,すなわち多重辺やループは含まれない
部分点
この問題には部分点が設定されている.この問題のテストケースのうち50点分は、追加で以下の制約も満たす.
- 1 \leq n1, n2 \leq 20
出力
2つのグラフの間に辺を1本追加してできあがるグラフの直径の最小値・最大値を空白スペース区切りで1行に出力せよ.
入力例1
4 5 0 1 0 2 0 3 1 2 2 3 4 5 0 1 0 2 0 3 1 2 2 3
入力例1に対する出力例
3 5
直径が3になる例と5になる例はそれぞれ以下の通り.
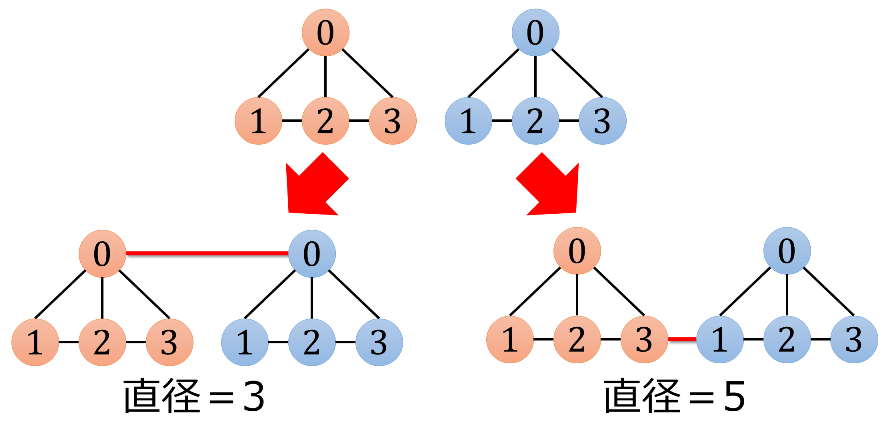
入力例2
6 5 0 1 1 2 2 3 3 4 4 5 6 5 0 1 1 2 2 3 3 4 4 5
入力例2に対する出力例
7 11
直径が7になる例と11になる例はそれぞれ以下の通り.
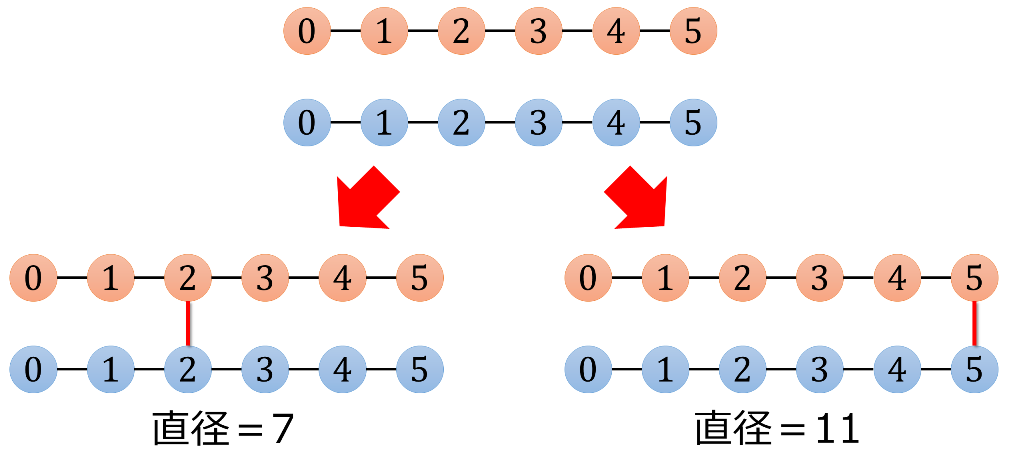
入力例3
7 6 0 1 1 2 2 3 3 4 4 5 5 6 2 1 0 1
入力例3に対する出力例
6 8
できあがるグラフの直径の最小値に注意せよ.
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国のお姫様は,データ構造が大好きだ.そこで王様は,お姫様の誕生日に「バイナリヒープを表現した配列」をたくさんプレゼントしようと準備していた.
「バイナリヒープを表現した配列」とは,配列の第 i 要素の値は,第2i+1要素が存在すればそれより真に小さく,同様に第2i+2要素が存在すればそれよりも真に小さい,という条件を全ての要素で満たす配列のことを言う.たとえば [0,1,4,2,3] はバイナリヒープを表現した配列である.なぜならば,第0要素である0は第1要素と第2要素である1と4よりも小さく,第1要素である1は第3要素と第4要素の2と3よりも小さい…,という条件がすべて成り立っている.このような配列は,第i要素の子が第2i+1要素と第2i+2要素であるようなツリー構造と考えると,親の方が常に値が小さいという特徴を持つ.お姫様は,この特徴を活用してソートなど様々なアルゴリズムの効率化をするのにご執心なのだ.
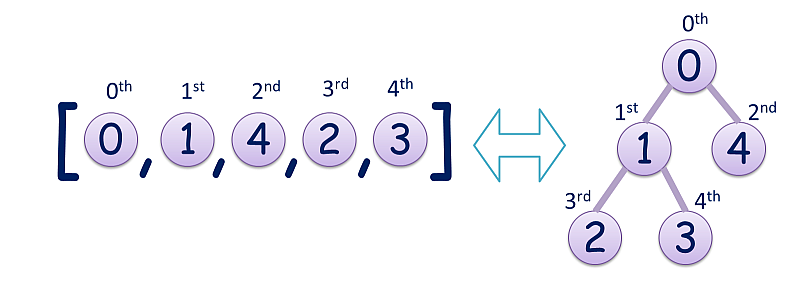
さて,ところが不運なことに,王様はせっかく作った「バイナリヒープを表現した配列」を落として壊してしまった!今や王様の手元には,「バイナリヒープを表現した配列」の後半部分しか手元に残っていない.一刻も早く元の「バイナリヒープを表現した配列」を復元しなくてはならない.王様は,元の配列の要素はすべて非負整数で,重複する値はなかったことを覚えている.この情報を手がかりに配列を復元して欲しい.
課題
すなわち,入力 A0 ... AN-1 に対し,次を満たす配列 H0 ... HM-1 を求め,その長さ M を答えとして出力して欲しい.
- Hi は全て 0 以上の整数
- 配列の要素は全て互いに異なる.つまり,i \neq j ならば Hi \neq Hj
- バイナリヒープを表現した配列となっている.つまり,常に Hi \lt H2i+1 かつ Hi \lt H2i+2
- A が H の接尾辞となっている.つまり,全ての 0 \leq k \lt N に対し,Ak = HM-N+k
複数の可能性がある場合は最小の M を答えること.条件を満たす H が存在しない場合は -1 と答えること.
配点
100
入力
入力は以下の形式で与えられる.
N A0 A1 ... AN-1
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq N \leq 100
- 0 \leq Ai \leq 109
- Ai は互いに相異なる非負整数
出力
問題の解を1行に出力せよ.
入力例1
3 4 2 3
入力例1に対する出力例
5
[4,2,3] は,4(第0要素)が2や3(第1,第2要素)よりも大きいので,条件を満たさない.[*,4,2,3] の形の配列も,4(第1要素)が3(第3 = 2 \times 1+1要素)よりも大きいので,*にどんな値を入れても条件を満たさない.[0,1,4,2,3] が,[4,2,3] を接尾辞に持ちバイナリヒープを表現した最短の配列である.
入力例2
3 3 1 2
入力例2に対する出力例
-1
[0,1,3,1,2] や [-1,0,3,1,2] は配列の要素に重複がないこと,非負整数であることなどに反するため,条件を満たさないことに注意せよ.
入力例3
4 10 20 40 30
入力例3に対する出力例
4
入力例4
4 9 2 3 6
入力例4に対する出力例
8
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国の王子様は,CNFが大好きだ.毎日,充足解を求め遊んでいた.そんな王子様もそろそろ充足可能性問題に飽きてきた.そこで王子様は,王様に変わった問題を出してもらうことにした.今度の問題は論理式だけでなく,変数の割り当ても入力されるようだ.
課題
2-SAT(satisfiability)とは,節の長さが(高々)2の乗法標準形で表された論理式(2-CNF)が与えられた時に,各変数にtrue/falseに適切に割り当てることで,論理式が充足可能であるかを判定する問題である.今,あなたは2-CNFと各変数へのtrue/falseの割り当てが与えられる.しかし,残念ながらこの変数割り当ては充足解ではないかもしれない.割り当てが充足解となるために必要な変数の割り当ての変更回数の最小値を求めよ.ただし,答えが11以上であるか論理式が充足不可能である場合には "TOO LARGE" と出力せよ.
配点
200
入力
入力は以下の形式で与えられる.
n m cnf a1a2...an
n は変数の数,m は節の数を表す. a1a2...an は変数の割当を表し,ai=T ならば変数 i の割当がtrueであり,ai=F ならば変数 i の割当がfalseであることを意味する.2-CNFは以下のBNFで与えられる.
- "^" は論理積,"v" は論理和,"~" は否定演算子を表す
- 各変数は 1,2,...,n-1,n で表される
<cnf> ::= <clause> | <clause>"^"<cnf>
<clause> ::= "("<literal>"v"<literal>")"
<literal> ::= <var> | "~"<var>
<var> ::= [1-9] | <var>[0-9]
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq n \leq 10000 (=104)
- 1 \leq m \leq 100000 (=105)
- BNF中の <var> の値は 1 から n である
出力
割り当てが充足解となるために必要な変数の割り当ての変更回数の最小値を一行に出力せよ.ただし,答えが11以上であるか論理式が充足不可能である場合には "TOO LARGE" と出力せよ.
入力例1
4 2 (~1v2)^(3v~4) TTFF
入力例1に対する出力例
0
この割り当てはすでに与えられた2-CNFを充足している.
入力例2
3 4 (~1v~2)^(1v3)^(2v~1)^(~3v1) FFT
入力例2に対する出力例
TOO LARGE
この2-CNFは充足解を持たない.
入力例3
22 11 (1v2)^(3v4)^(5v6)^(7v8)^(9v10)^(11v12)^(13v14)^(15v16)^(17v18)^(19v20)^(21v22) FFFFFFFFFFFFFFFFFFFFFF
入力例3に対する出力例
TOO LARGE
最低でも11個の変数の割当を変更しなければ,この2-CNFを充足させることはできない.
Time Limit: 2 sec / Memory Limit: 256 MB
問題文に修正があります (14:04)
問題に関して追記があります (13:25)
問題
背景
うなぎ王国では長らく通信の手段として伝書うなぎが使われてきたが,近年一瞬で声を伝達することができる魔法の糸が発明された.そこで王様は,この魔法の糸で町の間を繋ぐことによって通信網を整備することにした.魔法の糸の生産には時間がかかるので,はじめは親交の深い町同士でグループを作りその中でのみ通信できるようにし,徐々にグループを合併して広い範囲で通信できるようにするという計画を立てた.あるグループに含まれる町同士を魔法の糸で繋ぐにはどれだけの長さの魔法の糸が必要だろうか.
課題
頂点数 N ,辺数 M の連結な無向グラフ G が与えられる.それぞれの頂点には 0 ,..., N-1 の番号が対応している.辺には整数の長さが付いている. G 上の頂点を分割するグループについて考える. はじめは,頂点 0 , 1 ,..., N-1(14:04修正) はそれぞれ自身のみを含むグループに属しているとする.
2 つのグループを合併して新たなグループとする「合併クエリ」が Q 回与えられる.それぞれの合併クエリに対して,合併されてできた新たなグループに含まれる頂点のみ(13:25追記)を連結にするために必要な辺の集合で,その長さの和が最小となるものを求め,その和を出力せよ.
配点
200
入力
入力は以下の形式で与えられる.
N M u1 v1 w1 ... uM vM wM Q p1 q1 ... pQ qQ
N , M はそれぞれグラフの頂点数,辺数を表す.続く M 行は辺の情報を表す.ui, vi, wi は 頂点ui と 頂点viの間に長さ wi の辺があることを表す.Qは合併クエリの数を表す.続く Q 行は,頂点 pi を含むグループと頂点 qi を含むグループの合併クエリを表す.
制約
入力中の各変数は以下の制約を満たす.
- 2 \leq N \leq 2,000
- 1 \leq M \leq 200,000 (=2\times 105)
- 0 \leq ui, vi \lt N
- 1 \leq w_i \leq 100,000 (=105)
- 1 \leq Q \lt N
- 0 \leq pi, qi \lt N
- 与えられるグラフは連結であり,多重辺やループを含まない
- 既に同じグループに属している2点がクエリとして与えられることはない
出力
出力は Q 行からなる. i 行目には,i 番目の合併クエリで合併されたグループを連結にするために必要な辺の長さの和の最小値を出力せよ.ただし,そのような辺の集合が存在しない場合は "IMPOSSIBLE" と出力せよ.
入力例1
3 3 0 1 2 0 2 1 1 2 1 2 0 1 1 2
入力例1に対する出力例
2 2
はじめは,それぞれの頂点は自身のみを含むグループに属している.最初のクエリで頂点 0 を含むグループと頂点 1 を含むグループが合併される.合併したグループは頂点 0 と頂点 1 からなる.この 2 つの頂点を連結にするためには 1 本辺が必要であり,そのような辺の長さの最小値は 2 である.次のクエリで頂点 1 の属するグループと頂点 2 の属するグループが合併され,すべての頂点が 1 つのグループになる.このグループを連結にするような辺の長さの和の最小値は 2である.
入力例2
5 7 0 1 3 0 4 3 1 2 2 1 3 1 1 4 4 2 3 3 3 4 3 4 0 1 2 4 1 3 3 4
入力例2に対する出力例
3 IMPOSSIBLE 4 9
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国の学生たちはいつも学校の地下にある学生室で勉強している.学生室にはいつも学生がいるため普段はきれいに掃除されているが,夏休みになると学生が学校に来なくなるため,学生室は埃だらけになってしまう.そこで学生たちは夏休みの間も学校にやってきて学生室の掃除をすることにした.しかし学生たちは学校に来られる日が限られており,かつあまり学校に来たがらない.とりあえず各学生には一度ずつ掃除を頼むことにしたが,それでは十分ではないので何人かには毎日学校に来てもらおう.どういう割り当てにすれば学生室をきれいに保てるだろうか.
課題
最も長く掃除が行われない期間が最小になるように掃除の担当を割り当てたときに,その期間が何日になるかを答えよ.
学生の人数 N,夏休みの日数 M,パラメータ K が与えられる. i 番目の学生は ai から bi の間の日にしか学校に来ることはできない.また各学生に対して一度しか掃除を頼むことはできない.ただし K 人の学生を好きなように選んで,その学生には学校に来ることのできる期間に毎日学校に来てもらうように頼むことができる.
配点
200
入力
入力は以下の形式で与えられる.
N M K a1 b1 ... aN bN
N は学生の数,M は夏休みの日数,K は毎日学校に来る学生の数,ai,bi は i 番目の学生が学校に来ることのできる期間を表す.
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq N \leq 105
- 1 \leq M \leq 109
- 0 \leq K \leq N
- 1 \leq ai \leq bi \leq M
部分点
この問題には部分点が設定されている.この問題のテストケースのうち50点分は,追加で以下の制約も満たす.
- K=0
出力
問題の解を1行に出力せよ.
入力例1
1 2 0 1 2
入力例1に対する出力例
2
1日目に当番になっても2日目に当番になっても最長の間隔は2日になる.
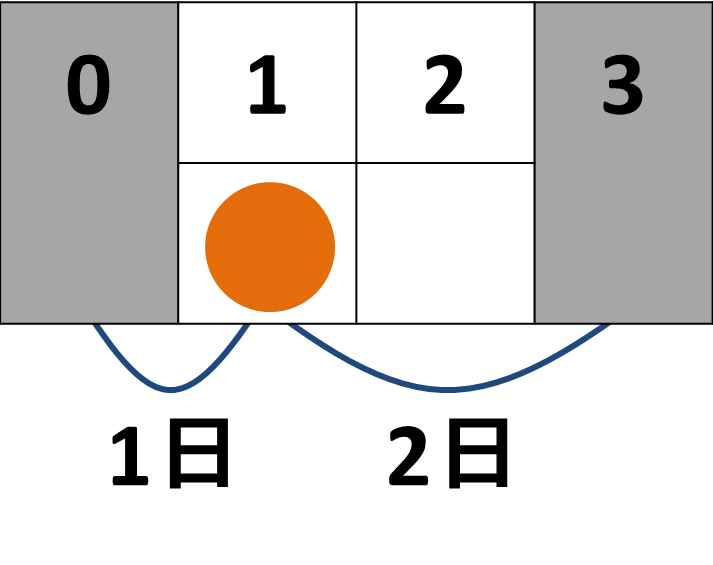
入力例2
1 2 1 1 2
入力例2に対する出力例
1
毎日学校に来ることができるので,最長の間隔は1日になる.
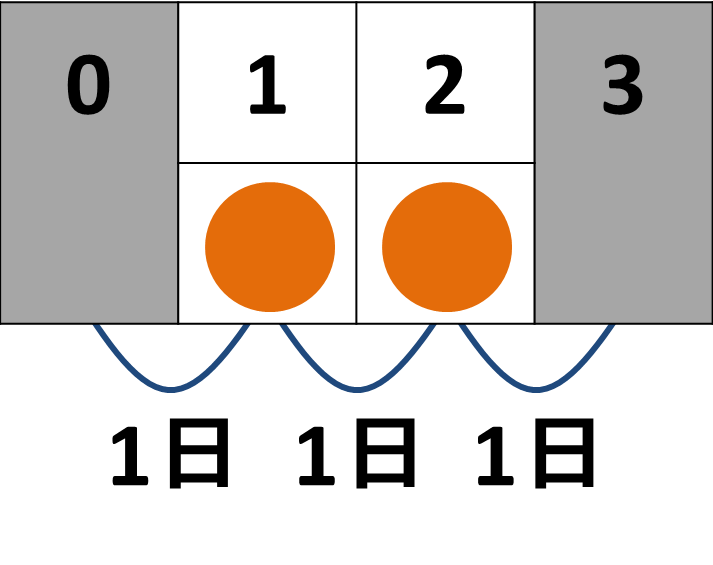
入力例3
2 6 1 2 2 4 5
入力例3に対する出力例
2
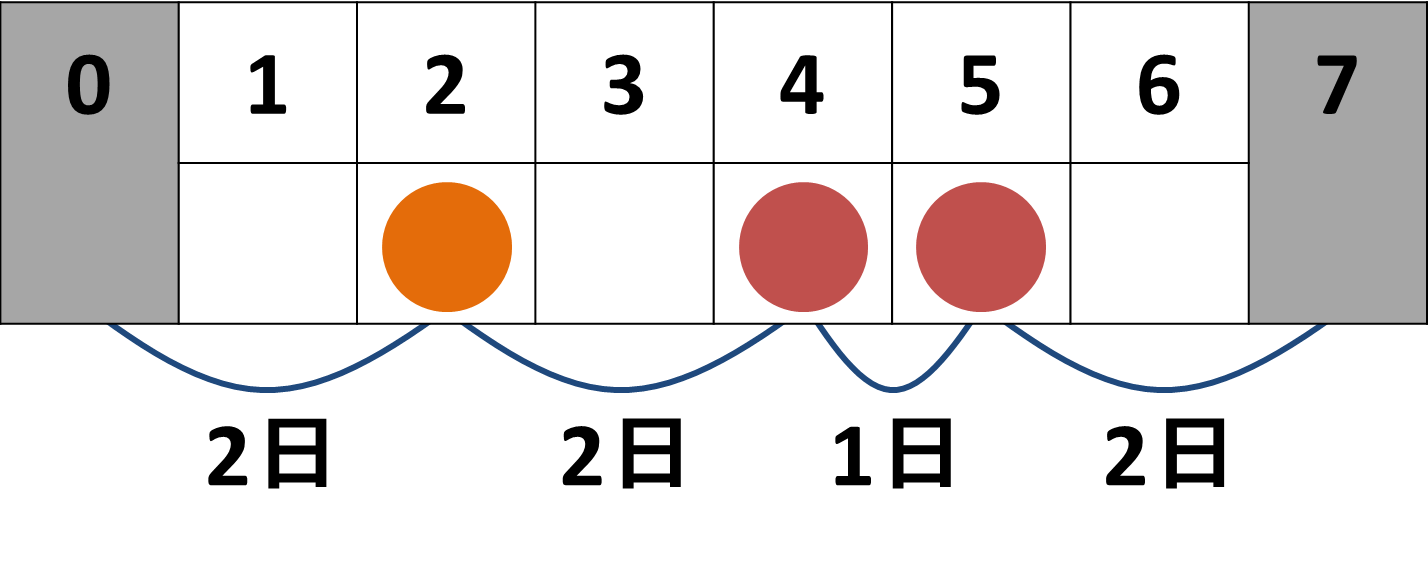
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うさぎ王国と友好関係を築いたうなぎ王国は,今度は宇宙に進出することにした.目標はうなぎ宇宙ステーションの建設である.しかしながら,無数の小惑星に邪魔をされ,広大な空間を占有することができない.そこで王様はレーザー砲を使い,邪魔な小惑星を破壊し尽くすことにした.
課題
N \times N の二次元格子上に M 個の小惑星がある.縦方向(x軸に垂直)もしくは横方向(y軸に垂直)にレーザーを打つことで全ての小惑星を破壊したい.発射されたレーザーは一直線に進み,途中の小惑星を全て貫通してダメージを与える.全てのレーザーは同時に発射され,その出力には,x軸に垂直に直線(x=i)に沿って最大で pi,y軸に垂直に直線(y=j)に沿って最大で qj の非負整数値を設定することが出来る.小惑星 k は,位置 (xk,yk) にあり,合計出力が ak 以上あれば破壊されるが,合計出力が bk より大きくなると爆発して非常に危険である.どの小惑星も爆発させることなく,全ての小惑星を破壊できるか判定せよ.
配点
200
入力
入力は以下の形式で与えられる.
N M p1 ... pN q1 ... qN x1 y1 a1 b1 ... xM yM aM bM
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq N \leq 1000 (=103)
- 1 \leq M \leq 100000 (=105)
- 1 \leq pi, qi \leq 1000000 (=106)
- 1 \leq xi, yi \leq N
- (xi, yi) \neq (xj, yj) (i \neq j)
- 1 \leq ak \leq bk \leq 2000000 (=2 \times 106)
出力
どの小惑星も爆発させることなく,全ての小惑星を破壊することが可能ならば "yes" ,不可能ならば "no" を一行に出力せよ.
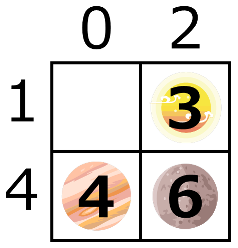
入力例1
2 3 1 2 3 4 2 1 3 5 1 2 3 4 2 2 6 6
入力例1に対する出力例
yes
下図のようにレーザーの出力を設定すれば,全ての小惑星を安全に破壊できる.
入力例2
2 3 1 2 3 4 2 1 1 1 1 2 2 3 2 2 5 7
入力例2に対する出力例
no
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国にはたくさんの町があり,これらの町は支配関係にあるが,その関係は木構造になっていることが知られている.それぞれの町はどこか別の町と友好関係を結びたいと考えているが,町同士が支配関係にある場合は友好関係を結ぶことができない.またそれぞれの町はその町とできるだけ人口が近い町と友好関係を結びたいと考えている.それぞれの町がどこの町と友好関係を結べばいいのかを考えよう.
課題
各頂点が値を持つ根付き木が与えられたときに,各頂点に対してその頂点の子孫でも祖先でもない頂点の中で,その頂点の持つ値に最も近い値を持つ頂点の値を答えよ.
最も近い値を持つ頂点が複数ある場合は,その中で最も小さい値を持つ頂点の値を答えよ.またその頂点の子孫でも祖先でもない頂点が存在しない頂点に対しては -1 を出力せよ.
配点
200
入力
入力は以下の形式で与えられる.
N a1 ... aN s1 t1 ... sN-1 tN-1
N は頂点の数,ai は i 番目の頂点が持つ値,si と ti は ti が si の子供であることを表す.
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq N \leq 105
- 1 \leq ai \leq 109
- 0 \leq si, ti \lt N
グラフは根付き木になっていることが保証される.
出力
出力は N 行からなる. i(1 \leq i \leq N) 行目には i 番目の頂点の子孫でも祖先でもない頂点の中で,その頂点の持つ値に最も近い値を持つ頂点の値を出力せよ.ただしその頂点の子孫でも祖先でもない頂点が存在しない頂点に対しては -1 を出力せよ.
入力例1
7 1 2 3 4 5 6 7 0 1 1 2 1 3 0 4 4 5 4 6
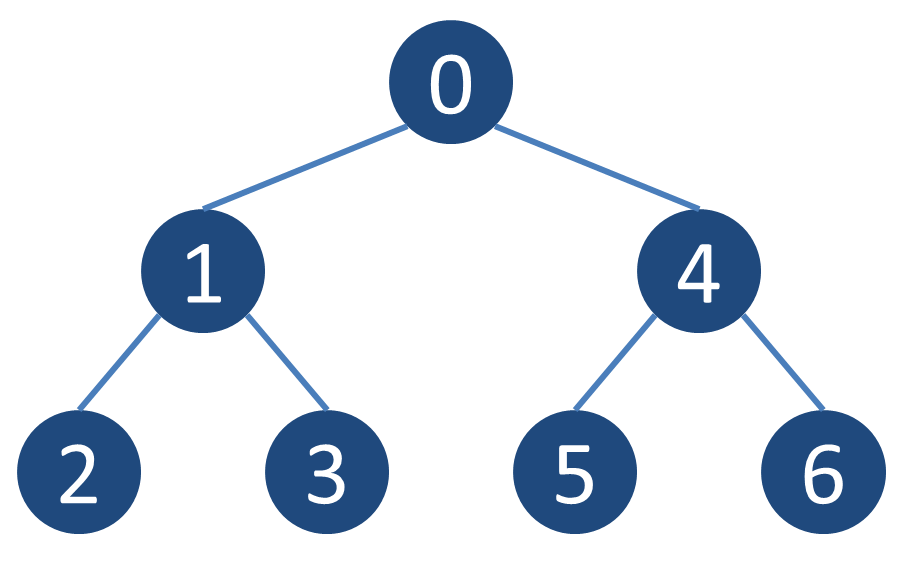
入力例1に対する出力例
-1 5 4 3 4 7 6
各頂点の子孫でも祖先でもない頂点がどのようになるかの一例を示す.例えば頂点1の子孫でも祖先でもない頂点は4,5,6であり,頂点2の子孫でも祖先でもない頂点は3,4,5,6のようになる.
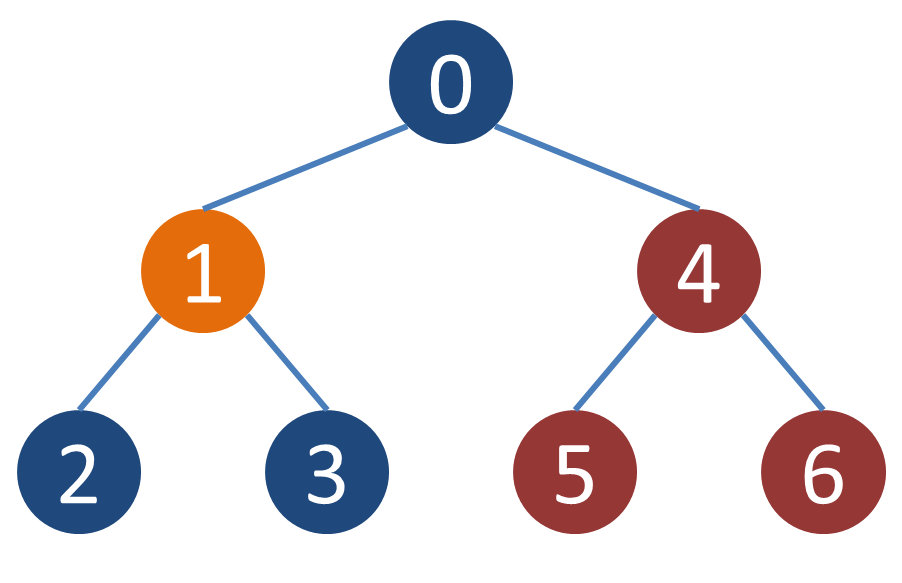
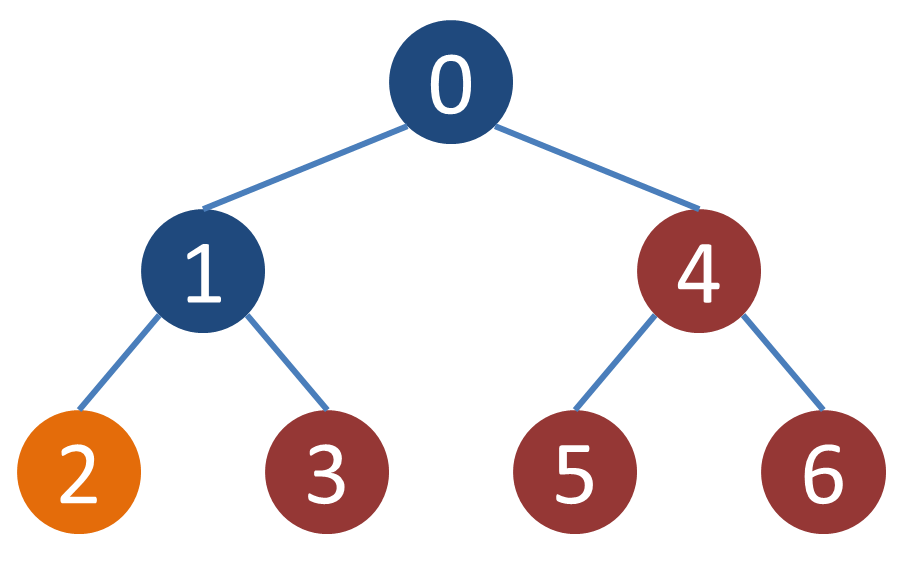
入力例2
4 1 2 3 4 0 1 1 2 2 3
入力例2に対する出力例
-1 -1 -1 -1
すべての頂点にその頂点の子孫でも祖先でもない頂点が存在しない.
入力例3
5 1 1 2 3 4 0 1 0 2 0 3 0 4
入力例3に対する出力例
-1 2 1 2 3
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国の王子様は運動不足であると王様や部下たちに指摘されている.そのため,うなぎ王国の王子様はお城の近辺を散歩したいと考えており,その経路を検討している.うなぎ王国の王子様は運動を極めて嫌うため,出来るだけ短い経路が良い.しかし,うなぎ王国の王子様はうなぎであるため体がとても長く,短すぎる経路では末尾がお城から出る前に頭部がお城に戻ってきてしまい,お城から出かけたということを認めてもらえなくなるかもしれない.そこで,適度に短い散歩のための経路を知りたい.
課題
あなたの仕事は,グラフが与えられたとき頂点 0 を出発し頂点 0 へ戻る経路であって 1, 2, ..., K 番目に短いものの長さをそれぞれ求めるプログラムを作成することである.
グラフは単純とは限らない(即ち自己閉路や多重辺は存在し得る). 経路中で同じ頂点を何度通っても構わない.特に,最初と最後以外で頂点 0 を通過してもよい. 経路は,通過した辺の列として区別される. 即ち,通過する頂点の列が等しくとも通過した辺が異なれば異なる経路とみなす. 経路の長さは通過した辺の重みの和として定義する. 本問題では,少なくとも辺を1本以上通過する経路のみを考える(即ち長さ 0 の経路は除外して考える). 長さが同じである2つの経路には任意に異なる順位を与えることとする. 即ち,頂点 0 を出発し頂点 0 へ戻る全ての経路を長さの昇順に並べた時の先頭 K 個の経路の長さを出力せよ.
ただし,軍事機密の都合上,うなぎ王国の地図は公開されない. 従って,本日のコンテストでは,以下のように乱数を用いて生成されたグラフによりプログラムの正誤判定を行う. グラフの M 本の辺は独立に生成される. 各辺について始点・終点がそれぞれ N 個の頂点から一様に選択される. 各辺の重みも 1 から 1,000,000,000 の整数として一様に選択される. 実際には,入力はこのプログラムを用いて生成された. 擬似乱数生成器の初期化に用いられるプログラムの第四引数の値は 1 以上 1,000,000 以下のいずれかの整数を用いた.
配点
200
入力
入力は以下の形式で与えられる.
N M K U1 V1 C1 U2 V2 C2 ... UM VM CM
最初の行の N,M はグラフの頂点数,枝数を表す.K は求める経路の数を表す.続く M 行はグラフの辺を表す. 各 i 行目は頂点 Ui,Vi 間に重み Ci の辺があることを表す.
制約
入力中の各変数は以下の制約を満たす.
- N = 25,000
- M = 105
- K = 105
- 入力は指定された方法によって生成されている(詳細は上記の通り)
- 0 \leq Ui,Vi \lt N
出力
出力は K 行からなる.i (1 \leq i \leq K) 行目には i 番目に短い経路の長さを出力せよ.ただし,そのような経路が存在しない場合は代わりに -1 を出力せよ.
入力例1
3 3 5 0 1 1 1 2 1 2 0 1
入力例1に対する出力例
3 6 9 12 15
この入力は N,M,K 及びグラフの生成法に関する制約を守っていないことに注意せよ. 以下に続く入力例も同様である.
入力例2
2 4 5 0 0 2 0 0 3 0 1 1000 0 1 10000
入力例2に対する出力例
2 3 4 5 5
グラフは単純とは限らず,自己閉路や多重辺が存在するかもしれない.
入力例3
3 3 3 0 1 1 0 2 1 1 2 1
入力例3に対する出力例
-1 -1 -1
経路の数が i 個より少ない場合,i 行目には -1 を出力する.グラフの辺は有向であることに注意せよ.
Time Limit: 2 sec / Memory Limit: 256 MB
問題
うなぎ王国のきたまさ君は今, Unagi The synthesis Programming Contest(略称: UTPC)で出題された次のような問題を解いている.
うさぎ王国には n 羽の若いオスのうさぎと n 羽の若いメスのうさぎが暮らしている. 各うさぎには 1〜2n までの番号が付いており,奇数番目がオスのうさぎ,偶数番目がメスのうさぎである. m 個の組 (a_1, b_1), ..., (a_m, b_m) が与えられ,これらは a_i 番(奇数)のオスと b_i 番(偶数)のメスが交際していることを表している. (一羽のうさぎが複数のうさぎと交際していることもある.これはうさぎの世界では常識である.) うさぎ王国のお姫様は最近うなぎ王国の王子様に振られたショックから,交際しているペアを見ていると無性に腹が立ってくる. そこで,何羽かのうさぎを国外追放することにより国内から交際しているペアを消滅させることを考えた. もちろん,国外追放するうさぎはできるだけ少ないほうが良い. そのような方法をひとつ求め,追放すべきうさぎの番号の列を出力せよ.
離散数学を極めたきたまさ君は,これは「二部グラフの最小頂点被覆」を求める問題であると瞬時に理解した. きたまさ君によると,この問題は次のようにして解くことができるらしい.
- 各うさぎをグラフの頂点だと思い,始点から各オスのうさぎに向かって容量1の辺を,各メスのうさぎから終点に向かって容量1の辺を張る.
- 各ペア (a_i,b_i) について a_i 番の頂点から b_i 番の頂点に向かって容量1の辺を張る.
- 始点から終点に向かう最大流を求める.
- 流量のある辺を除去して逆向きに付け替えたグラフ(残余グラフ)を考え,そのグラフ上で始点から到達不能なオスと到達可能なメスからなる集合が求めたい最小解.
きたまさ君はこのアルゴリズムを一瞬で実装し,提出したところ,Wrong Answer の判定を食らってしまった. きたまさ君は「天才である僕がプログラムにバグを埋め込むはずがない.出題側がなにかミスをしているのだろう.」と疑ったところ,複数の最小解がありうるにも関わらず, UTPCで使われている KMCoder というジャッジシステムでは完全一致でしか正誤が判定できない仕様になっていることに気がついた. 出題者の気持ちをエスパーしたきたまさ君は,おそらく複数ありうる解のうちで辞書順最小のものを答えれば良いはずだと考えたが,天才であるきたまさ君をもってしても辞書順最小頂点被覆はどうやって求めればいいのか分からなかった. きたまさ君のプログラムの続きを手伝ってあげよう.
※本東京大学プログラミングコンテスト(UTPC)で使われているジャッジシステム AtCoder では,KMCoder と違い,完全一致以外での正誤判定も行うことが出来る.配点
300
入力
入力は以下の形式で与えられる.
n m a1 b1 f1 ... am bm fm
n, m, a_i, b_i は文中で記された通りであり,a_iは奇数,b_iは偶数である. f_iはきたまさ君のプログラムにより求めた最大流において,頂点 a_i から頂点 b_i への辺に流れている流量 (0 もしくは 1) を表す. きたまさ君の求めた最大流が本当に最大流であることは保証されているが,どうしても信じられない場合は各自で最大流を求めても構わない.
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq n,m \leq 105
出力
追放すべきうさぎの集合のうちで辞書順最小のものを求め,一行目にその大きさ C ,続く C 行にうさぎの番号を小さい順に一つずつ出力せよ. ただし,集合 X が集合 Y より辞書順で小さいとは,それぞれ番号を小さい順に x_1,x_2,...,x_C と y_1,y_2,...,y_C とした時,ある kが存在して i=1,2,...,k-1についてx_i=y_iかつx_k\lt y_kとなることと定義する.
入力例1
4 6 1 2 1 3 4 1 3 6 0 5 2 0 7 2 0 7 8 1
入力例1に対する出力例
3 2 3 7
入力例2
4 8 1 2 1 1 4 0 3 4 1 3 6 0 5 2 0 5 6 1 5 8 0 7 8 1
入力例2に対する出力例
4 1 3 5 7
入力例3
2 2 1 4 1 3 2 1
入力例3に対する出力例
2 1 2
Time Limit: 2 sec / Memory Limit: 256 MB
問題
背景
うなぎ王国の隣国うさぎ王国の前国王は,道路に関所を作るのが大好きだった.王国の至る所に,通るたびに 1 ウサドル(ウサドルはうさぎ王国の通貨単位)の通行税が取られる道が残っている.
現在のうさぎ国王はこれを廃止し国民の負担を減らしたいと考えたが,前国王派の勢力は根強く,なかなか関所を取り潰すことができない.相談を受けたうなぎ王国の王様は,この問題を解決する画期的な提案を行った.前国王派の勢力の弱い関所のない道に,通るたびに 1 ウサドルの報奨金が手渡される「逆関所」を設置してしまうのだ.こうすることで通行人の収支のバランスがとれるようになり,うさぎ王国には平和が訪れた.
さて,うさぎ王国に住まう青年うさぎ Jiro は潔癖な性格であった.国王の善意に甘えて逆関所ばかりを通りお金を稼ぐような行為は,彼には考えられない.例え遠回りになっても,同じ道を何度も回ることになろうとも,Jiro はどこへ行くにも関所と逆関所による収支がトータルで ±0 になるようなルートをとることにしている.
しかし一方で,Jiro はその潔癖な性格が災いしたため,貧乏である.どこかに出かけようとする時は,いつも所持金は 0 ウサドルなのである.あなたには,そんな Jiro のための最短経路計算プログラムを書いて欲しい.
課題
0 から N-1 の番号のついた N 頂点からなる有向グラフが与えられる.このグラフの辺は正整数の長さを持ち,また,以下の3種類の文字で表されるタイプに分類される.
- '-': 「関所」.一回通るたびに所持金が 1 減る.所持金 0 の時はこのタイプの辺は通れない.
- '+': 「逆関所」.一回通るたびに所持金が必ず 1 増える.
- '=': なにもない普通の道.所持金は変化しない.
うさぎの Jiro は所持金 0 で頂点 0 を出発し,最終的に所持金 0 で頂点 N-1 に到達したい.このような経路の最短の長さを求めよ.経路中で同じ頂点や辺を何度通っても構わない.特に,最初と最後以外で頂点 0 と N-1 を通過してもよい.
配点
300
入力
入力は以下の形式で与えられる.
N G0 ... GN-1 L0,0 ... L0,N-1 ... LN-1,0 ... LN-1,N-1
N は頂点数,Gi=Gi,0Gi,1...Gi,N−1 は長さ N の文字列で Gi,j は頂点 i から頂点 j への辺のタイプを表す. Gi,j='x' ならば頂点 i から頂点 j には辺は存在しない.Li,j は自然数で,0 ならば頂点 i から頂点 j への辺が存在しないこと,そうでなければ頂点 i から頂点 j への辺の長さを示す.
制約
入力中の各変数は以下の制約を満たす.
- 2\leq N\leq 250
- すべての i について Gi,i='x'
- すべての i, j について Gi,j='x' ならば Li,j=0 ,それ以外の場合 0\lt Li,j \lt 10,000
部分点
この問題には部分点が設定されている.この問題のテストケースのうち50点分は,追加で以下の制約も満たす.
- 2 \leq N \leq 50
出力
問題の解を1行に出力せよ.条件を満たす経路が存在しない場合は -1 と出力せよ.
入力例1
5 x+x=x xx-xx x+x+- xxxx- xxxxx 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0
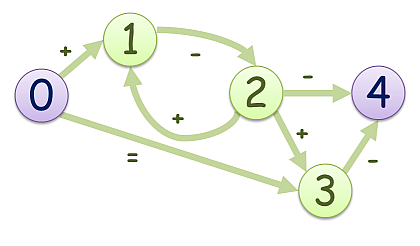
入力例1に対する出力例
4
頂点0(所持金0) → 頂点1(所持金1) → 頂点2(所持金0) → 頂点3(所持金1) → 頂点4(所持金0) という経路が解となる.これより短い経路では終点に到達したときの所持金が0にならない.
入力例2
4 x+=x +xxx =xx- xx-x 0 1 1 0 1 0 0 0 1 0 0 1 0 0 1 0
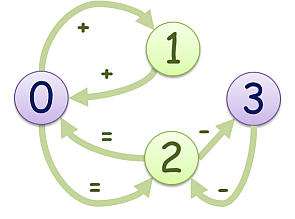
入力例2に対する出力例
-1
始点から終点への経路は存在するが,所持金がちょうど0の状態で終点に到達することはできない.
入力例3
3 x-- =x+ ==x 0 58 58 42 0 58 42 42 0
入力例3に対する出力例
-1
頂点1から出る辺はすべて '-' であるため,所持金0では動くことができない.
入力例4
8 x+xxxxxx xx+x=xxx +xxxxxxx xxxx-xxx xxxxx-xx xxxxxx-x xxxxxxx- xxx-xxxx 0 1 0 0 0 0 0 0 0 0 2 0 3 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 2 0 0 0 1 0 0 0 0
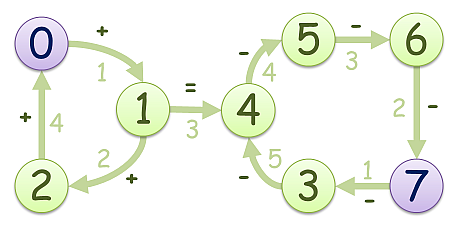
入力例4に対する出力例
71
始点や終点,またそれぞれの辺を何度も繰り返し通ってもよい.