Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given a graph G consisting of N vertices numbered 1, 2, \ldots, N. Initially, G has no edges.
You will add M undirected edges to G. The final shape of the graph is predetermined, and the i-th edge to be added (1 ≤ i ≤ M) connects vertices u_i and v_i. We will refer to this as edge i.
It is guaranteed that the resulting graph will be simple.
Determine if there exists a permutation (P_1, P_2, \ldots, P_M) of (1, 2, \ldots, M) that satisfies the following conditions, and if such a permutation exists, show an example.
Conditions
You must be able to add all M edges to G by following this procedure:
- For i = 1, 2, \dots, M, repeat the following:
- If there is already a cycle in G containing either vertex u_{P_i} or vertex v_{P_i}, the condition is not satisfied, and the procedure ends.
- Add edge P_i (the undirected edge connecting u_{P_i} and v_{P_i}) to G.
You are given T test cases; solve each of them.
What is a cycle?
A cycle in G is defined as a sequence of vertices (v_0, \dots, v_{L - 1}) and a sequence of edges (e_0, \dots, e_{L - 1}) that satisfy the following conditions:
- L \ge 1
- i \neq j \implies v_i \neq v_j, e_i \neq e_j
- For 0 \le i \le L - 2, edge e_i connects vertices v_i and v_{i+1}
- Edge e_{L-1} connects vertices v_{L-1} and v_0
What does it mean for a graph to be simple?
A graph G is simple if it contains no self-loops or multiple edges.Constraints
- All input values are integers.
- 1 \le T \le 2000
- For each test case:
- 2 \le N \le 4000
- 1 \le M \le 4000
- 1 \le u_i, v_i \le N\ (1 ≤ i ≤ M)
- The graph formed by adding all given edges is simple.
- The sum of N over all test cases is at most 4000.
- The sum of M over all test cases is at most 4000.
Subtasks
30 points will be awarded for passing the test set satisfying:
- T \le 50
- For each test case:
- N \le 100
- M \le 100
- The sum of N over all test cases is at most 100.
- The sum of M over all test cases is at most 100.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Here, \text{case}_i\ (1 ≤ i ≤ T) represents the i-th test case. Each test case is given in the following format:
N M u_1 v_1 u_2 v_2 \vdots u_M v_M
Output
For each test case, if a permutation (P_1, P_2, \ldots, P_M) satisfying the conditions exists, output such a P separated by spaces. If no such permutation exists, output -1.
Sample Input 1
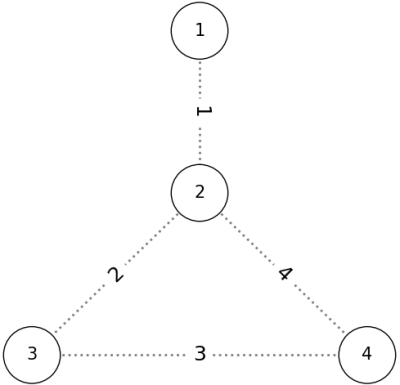
1 4 4 1 2 2 3 3 4 4 2
Sample Output 1
2 4 1 3
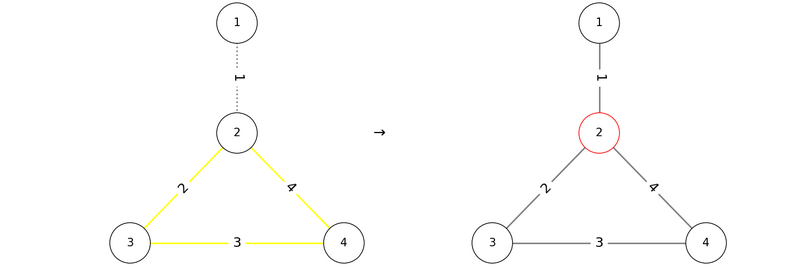
The given graph has the following shape:
If we add the edges in the order P = (1, 2, 3, 4), the conditions are satisfied as shown below:
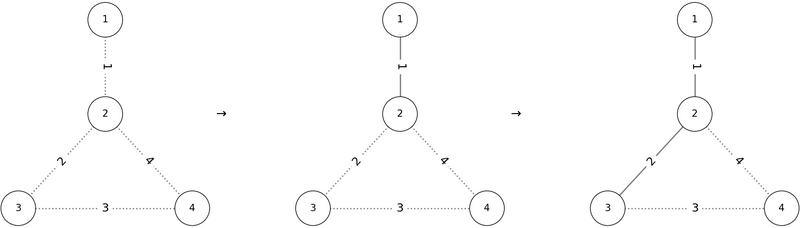
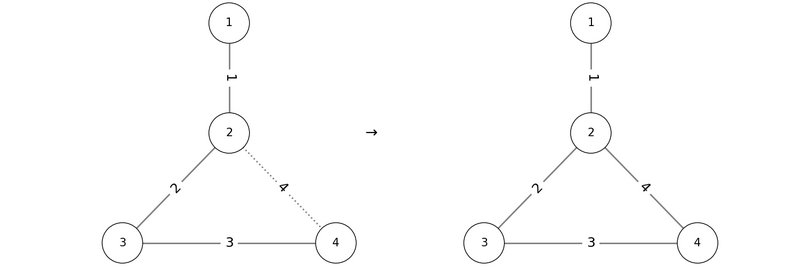
Thus, 1 2 3 4 is one valid output.
However, if we add edges in the order P = (2, 3, 4, 1), a cycle containing vertex 2 is created before edge 1 can be added, so the conditions are not satisfied.
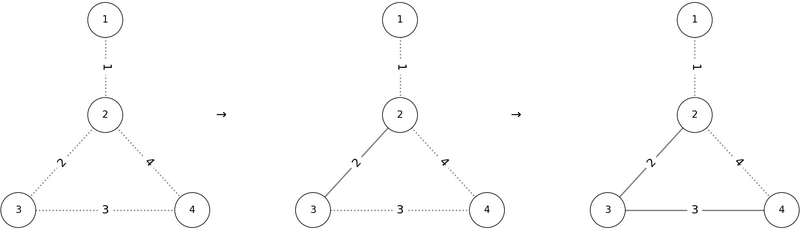
Other valid outputs include P = (1, 4, 3, 2) or P = (2, 4, 1, 3).
Sample Input 2
4 4 5 1 2 2 3 3 4 3 1 1 4 5 3 1 2 2 3 3 4 9 10 3 5 1 8 5 8 4 9 6 7 7 9 1 2 1 4 2 4 4 6 8 10 1 4 3 8 2 5 3 4 1 5 5 8 2 8 5 7 4 5 3 7
Sample Output 2
-1 3 2 1 4 10 2 8 7 9 6 5 3 1 -1
If no valid P exists, output -1. Note that the graph is not necessarily connected.
配点 : 100 点
問題文
N 頂点からなるグラフ G があり、頂点には 1, 2, \ldots, N の番号がついています。はじめ、G には辺がありません。
これから、G に M 本の無向辺を追加します。追加後のグラフの形は決まっており、追加する辺のうち i 番目の辺 (1 ≤ i ≤ M) は頂点 u_i と頂点 v_i を結ぶ辺です。これを辺 i と呼ぶことにします。
追加後のグラフは単純であることが保証されます。
(1, 2, \ldots, M) の順列 (P_1, P_2, \ldots, P_M) であって以下の条件を満たすようなものが存在するかどうか判定し、存在する場合はその一例を示してください。
条件
以下の手順を行って、G に M 本の辺をすべて追加することができる。
- i = 1, 2, \dots, M の順に以下を繰り返す:
- G に頂点 u_{P_i} または頂点 v_{P_i} を含むサイクルが存在するとき、条件は満たされないものとして手順を終了する。
- G に辺 P_i(頂点 u_{P_i} と頂点 v_{P_i} を結ぶ無向辺)を追加する。
T 個のテストケースが与えられるので、それぞれについて解いて下さい。
サイクルとは?
G におけるサイクルとは、頂点の列 (v_0, \dots, v_{L - 1}) と 辺の列 (e_0, \dots, e_{L - 1}) であって以下の条件を満たすもののことを言います。
- L \ge 1
- i \neq j \implies v_i \neq v_j, e_i \neq e_j
- 0 \le i \le L - 2 に対して、辺 e_i は頂点 v_i と頂点 v_{i+1} を結ぶ
- 辺 e_{L-1} は頂点 v_{L-1} と頂点 v_0 を結ぶ
グラフが単純とは?
グラフ G が単純であるとは、G が自己ループ及び多重辺を含まない事を言います。制約
- 入力はすべて整数
- 1 \le T \le 2000
- 各テストケースについて:
- 2 \le N \le 4000
- 1 \le M \le 4000
- 1 \le u_i, v_i \le N\ (1 ≤ i ≤ M)
- 与えられるすべての辺を追加したグラフは単純
- 各入力ファイルについて、N, M の総和はそれぞれ 4000 を超えない
部分点
以下の制約を満たすデータセットに正解した場合は 30 点が与えられる。
- T \le 50
- 各テストケースについて:
- N \le 100
- M \le 100
- 各入力ファイルについて、N, M の総和はそれぞれ 100 を超えない
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
ここで、\text{case}_i\ (1 ≤ i ≤ T) は i 番目のテストケースを表す。各テストケースは以下の形式で与えられる。
N M u_1 v_1 u_2 v_2 \vdots u_M v_M
出力
各テストケースについて、条件を満たす順列 (P_1, P_2, \ldots, P_M) が存在する場合は、そのような P を空白区切りで出力せよ。存在しない場合は、-1 を出力せよ。
入力例 1
1 4 4 1 2 2 3 3 4 4 2
出力例 1
2 4 1 3
与えられたグラフは以下の図のような形をしています。

これに対し、P = (1, 2, 3, 4) の順で辺を追加すると、以下の図のように条件を満たします。


したがって、1 2 3 4 は正しい出力の 1 つです。
しかし、P = (2, 3, 4, 1) の順で辺を追加すると、辺 1 を追加する際に頂点 2 を含むサイクルが存在するため、条件を満たしません。


他にも、P = (1, 4, 3, 2) や P = (2, 4, 1, 3) などが条件を満たします。
入力例 2
4 4 5 1 2 2 3 3 4 3 1 1 4 5 3 1 2 2 3 3 4 9 10 3 5 1 8 5 8 4 9 6 7 7 9 1 2 1 4 2 4 4 6 8 10 1 4 3 8 2 5 3 4 1 5 5 8 2 8 5 7 4 5 3 7
出力例 2
-1 3 2 1 4 10 2 8 7 9 6 5 3 1 -1
条件を満たす P が存在しない場合、-1 を出力して下さい。また、グラフは連結とは限らないことに注意してください。
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given a sequence S of length N, consisting of integers 1, 2, and 3. Determine the number of sequences A consisting of integers 1 and 2 such that the sequence T obtained after performing the following procedure matches S. Output the answer modulo 998244353. It can be proven that the number of such sequences A is finite.
Start with an empty sequence T. Given a sequence A consisting of integers 1 and 2, perform the following process to obtain the sequence T:
- Set a variable C = 0.
- If A contains at least one 1, remove the first occurrence of 1 from A and add 1 to C.
- If A is not empty, remove the first element x of A and add x to C.
- Append C to the end of T.
- If A is empty, terminate the process. Otherwise, return to step 1.
Constraints
- All input values are integers.
- 1 \le N \le 10^6
- 1 \le S_i \le 3
Input
The input is given from Standard Input in the following format:
N S_1 S_2 \dots S_N
Output
Output the number of sequences A that satisfy the conditions, modulo 998244353.
Sample Input 1
2 3 2
Sample Output 1
5
There are 5 possible sequences A that result in T = (3, 2): A = (1, 2, 2), (2, 1, 2), (2, 2, 1), (2, 1, 1, 1), (1, 2, 1, 1).
For example, for A = (2, 1, 1, 1), the process proceeds as follows:
- Remove the first occurrence of 1 in A, which is A_2 = 1. Now A = (2, 1, 1) and C = 1.
- Remove the first element of A, which is A_1 = 2. Now A = (1, 1) and C = 3.
- Append C to the end of T. Now T = (3).
- Remove the first occurrence of 1 in A, which is A_1 = 1. Now A = (1) and C = 1.
- Remove the first element of A, which is A_1 = 1. Now A = () and C = 2.
- Append C to the end of T. Now T = (3, 2).
Sample Input 2
6 3 2 2 3 2 1
Sample Output 2
4
Sample Input 3
5 3 2 1 3 2
Sample Output 3
0
Note that there may be cases where no sequence A produces S, in which case the answer is 0.
配点 : 100 点
問題文
1, 2, 3 からなる長さ N の数列 S が与えられます。1, 2 からなる数列 A であって、以下の問題の答えが S になるようなものの個数を 998244353 で割ったあまりを求めてください。ここで、求める数列 A の個数は有限となることが示せます。
空の数列 T があります。 1, 2 からなる数列 A が与えられます。次の処理を行った後の数列 T を求めてください。
- 変数 C を C = 0 として初期化する。
- A に 1 が含まれるならば、1 のうち最も先頭に近いものを A から取り除き、C に 1 を加算する。
- A が空でないならば、先頭の要素 x を A から取り除き、C に x を加算する。
- T の末尾に C を追加する。
- A が空ならば処理を終了する。そうでないなら 1. に戻る。
制約
- 入力はすべて整数
- 1 \le N \le 10^6
- 1 \le S_i \le 3
入力
入力は以下の形式で標準入力から与えられる。
N S_1 S_2 \dots S_N
出力
条件を満たす数列 A の個数を 998244353 で割ったあまりを出力せよ。
入力例 1
2 3 2
出力例 1
5
問題の答えが (3,2) となる数列 A は (1,2,2), (2,1,2), (2,2,1), (2,1,1,1), (1,2,1,1) の 5 通りです。
例えば (2,1,1,1) の場合は、以下のように問題は処理されます。
- A の 1 のうち最も先頭に近いものである A_2 = 1 を削除する。A = (2,1,1), C = 1 となる。
- A の先頭の要素である A_1 = 2 を削除する。 A = (1,1), C = 3 となる。
- C を T の末尾に追加する。 T = (3) となる。
- A の 1 のうち最も先頭に近いものである A_1 = 1 を削除する。 A = (1), C = 1 となる。
- A の先頭の要素である A_1 = 1 を削除する。 A = (), C = 2 となる。
- C を T の末尾に追加する。 T = (3, 2) となる。
入力例 2
6 3 2 2 3 2 1
出力例 2
4
入力例 3
5 3 2 1 3 2
出力例 3
0
問題の答えが S となる数列 A の個数が 0 個の場合もあります。
Time Limit: 6 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given an undirected graph G with 2^N + 1 vertices and 2^{N+1} - 1 edges. The vertices are numbered 0, 1, \dots, 2^N, and the edges are numbered 1, 2, \dots, 2^{N+1}-1.
Each edge in G belongs to one of N+1 types, ranging from type 0 to type N.
For type i (0 \le i \le N), there are exactly 2^i edges, which are numbered 2^i+0, 2^i+1, \dots, 2^i+(2^i-1). The edge numbered 2^i + j (0 \leq j \leq 2^i - 1) is an undirected edge of length C_{2^i + j} that connects vertex j \times 2^{N-i} and vertex (j+1) \times 2^{N-i}.
For example, when N = 3, G looks like the following graph:
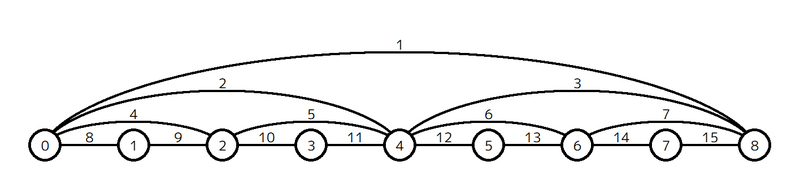
You are given Q queries to process. There are two types of queries:
1 j x: Change the length of edge j to x.2 s t: Find the shortest path length from vertex s to vertex t.
Constraints
- All input values are integers.
- 1 \le N \le 18
- 1 \le C_j \le 10^7 (1 \le j \le 2^{N+1}-1)
- 1 \le Q \le 2 \times 10^5
- In the query
1 j x, 1 \le j \le 2^{N+1}-1 and 1 \le x \le 10^7. - In the query
2 s t, 0 \le s < t \le 2^N. - There is at least one
2 s tquery.
Partial Score
30 points will be awarded for passing the testset satisfying the additional constraint: There is no 1 j x query.
Input
The input is given in the following format. Note that vertex numbering starts from 0, while edge numbering starts from 1.
N
C_1 C_2 \cdots C_{2^{N+1}-1}
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
Here, \text{query}_i represents the i-th query. Each query is given in one of the following formats:
1 j x
2 s t
Output
Let m be the number of queries of type 2 s t. Output m lines, where the i-th line contains the answer to the i-th 2 s t query.
Sample Input 1
3 7 1 14 3 9 4 8 2 6 5 5 13 8 2 3 10 2 0 1 2 0 4 2 4 6 2 4 8 2 3 5 1 6 30 2 3 5 2 4 6 1 1 10000000 2 0 8
Sample Output 1
2 1 4 8 17 18 13 15
- In the 1st query, using edge 8, the path 0 \to 1 results in a total distance of 2.
- In the 2nd query, using edge 2, the path 0 \to 4 results in a total distance of 1.
- In the 3rd query, using edge 6, the path 4 \to 6 results in a total distance of 4.
- In the 4th query, using edges 2, 1, the path 4 \to 0 \to 8 results in a total distance of 8.
- In the 5th query, using edges 11, 6, 13, the path 3 \to 4 \to 6 \to 5 results in a total distance of 17.
- In the 6th query, the length of edge 6 is updated from 4 to 30.
- In the 7th query, using edges 11, 12, the path 3 \to 4 \to 5 results in a total distance of 18.
- In the 8th query, using edges 2, 1, 15, 14, the path 4 \to 0 \to 8 \to 7 \to 6 results in a total distance of 13.
- In the 9th query, the length of edge 1 is updated from 7 to 10000000.
- In the 10th query, using edges 2, 3, the path 0 \to 4 \to 8 results in a total distance of 15.
配点 : 100 点
問題文
2^N + 1 頂点 2^{N+1} - 1 辺の無向グラフ G が与えられます。頂点には 0, 1, \dots, 2^N の番号が、辺には 1, 2, \dots, 2^{N+1}-1 の番号が割り振られています。
G の辺にはタイプ 0 からタイプ N までの N+1 個の種類があります。
タイプ i (0 \le i \le N) の辺は全部で 2^i 本あり、番号 2^i+0, 2^i+1, \dots, 2^i+(2^i-1) が割り当てられています。番号 2^i + j (0 \le j \le 2^i-1) の辺は、頂点 j \times 2^{N-i} と頂点 (j+1) \times 2^{N-i} を結ぶ長さ C_{2^i + j} の無向辺です。
例えば N = 3 の場合、G は以下のようなグラフになります。

Q 個のクエリが与えられるので、順に処理してください。与えられるクエリには以下の 2 種類があります。
1 j x: 辺 j の長さを x に変更する。2 s t: 頂点 s から頂点 t への最短経路の長さを求める。
制約
- 入力はすべて整数
- 1 \le N \le 18
- 1 \le C_j \le 10^7 (1 \le j \le 2^{N+1}-1)
- 1 \le Q \le 2 \times 10^5
1 j xのクエリにおいて、1 \le j \le 2^{N+1}-1 かつ 1 \le x \le 10^7 である2 s tのクエリにおいて、0 \le s < t \le 2^N である2 s tのクエリが 1 つ以上存在する
部分点
以下の制約を満たすデータセットに正解した場合は 30 点が与えられる。
1 j xのクエリが存在しない
入力
入力は以下の形式で与えられる。頂点番号は 0 から始まるのに対し、辺番号は 1 から始まることに注意せよ。
N
C_1 C_2 \cdots C_{2^{N+1}-1}
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
ここで、\text{query}_i は i 個目のクエリを表す。各クエリは以下のいずれかの形式で与えられる。
1 j x
2 s t
出力
2 s t のクエリの個数を m として、m 行出力せよ。そのうち i 行目には、i 個目の 2 s t のクエリの答えを出力せよ。
入力例 1
3 7 1 14 3 9 4 8 2 6 5 5 13 8 2 3 10 2 0 1 2 0 4 2 4 6 2 4 8 2 3 5 1 6 30 2 3 5 2 4 6 1 1 10000000 2 0 8
出力例 1
2 1 4 8 17 18 13 15
- 1 個目のクエリでは、辺 8 を用いて 0 \to 1 と移動することで最短距離 2 を達成できます。
- 2 個目のクエリでは、辺 2 を用いて 0 \to 4 と移動することで最短距離 1 を達成できます。
- 3 個目のクエリでは、辺 6 を用いて 4 \to 6 と移動することで最短距離 4 を達成できます。
- 4 個目のクエリでは、辺 2, 1 を用いて 4 \to 0 \to 8 と移動することで最短距離 8 を達成できます。
- 5 個目のクエリでは、辺 11, 6, 13 を用いて 3 \to 4 \to 6 \to 5 と移動することで最短距離 17 を達成できます。
- 6 個目のクエリでは、辺 6 の長さを 4 から 30 に変更します。
- 7 個目のクエリでは、辺 11, 12 を用いて 3 \to 4 \to 5 と移動することで最短距離 18 を達成できます。
- 8 個目のクエリでは、辺 2, 1, 15, 14 を用いて 4 \to 0 \to 8 \to 7 \to 6 と移動することで最短距離 13 を達成できます。
- 9 個目のクエリでは、辺 1 の長さを 7 から 10000000 に変更します。
- 10 個目のクエリでは、辺 2, 3 を用いて 0 \to 4 \to 8 と移動することで最短距離 15 を達成できます。
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given two sequences of non-negative integers A and B, each of length N. Initially, A=(A_1, A_2, \ldots, A_N) and B=(B_1, B_2, \ldots, B_N).
You will be given Q queries. Process them in the order they are given.
Each query is one of the following two types:
- Type 1: Given in the format
1 i a b. Update the value of A_i to a and the value of B_i to b. - Type 2: Given in the format
2 Y 0 0. Solve the following problem:For a non-negative integer S, define a sequence of non-negative integers X = (X_0, X_1, \dots, X_N) using the following recurrence:
- X_0 = S
- For each 1 \le i \le N, X_i = \begin{cases} X_{i - 1} \oplus A_i & \text{if } X_{i - 1} \equiv 1 \pmod{2} \\ X_{i - 1} \oplus B_i & \text{if } X_{i - 1} \equiv 0 \pmod{2} \end{cases}
Determine whether it is possible to set a non-negative integer S such that X_N = Y. If possible, output the smallest such S.
If no such S exists, output-1.
Constraints
- All inputs are integers.
- 1 \le N \le 2 \times 10^5
- 1 \le Q \le 2 \times 10^5
- 0 \le A_i, B_i < 2^{60} \ (1 \le i \le N)
- For a Type 1 query, 1 \le i \le N, 0 \le a, b < 2^{60}
- For a Type 2 query, 0 \le Y < 2^{60}
- There is at least one Type 2 query.
Partial Score
30 points will be awarded for passing the test set satisfying the additional constraint Q=1.
Input
The input is given in the following format:
N Q
A_1 A_2 \ldots A_N
B_1 B_2 \ldots B_N
\mathrm{query}_1
\vdots
\mathrm{query}_Q
Here, \mathrm{query}_i represents the i-th query and is given in one of the following formats:
1 i a b
2 Y 0 0
Output
Let q be the number of Type 2 queries. Output q lines, where the i-th line contains the answer to the i-th Type 2 query.
Sample Input 1
1 3 0 1 2 5 0 0 2 6 0 0 2 7 0 0
Sample Output 1
4 -1 6
Given A = (0),\ B = (1), the value of X_N is:
- X_N = S if S is odd.
- X_N = S \oplus 1 if S is even.
For the first query with Y = 5, both S = 4 and S = 5 result in X_N = 5, so the smallest S is 4.
For the second query with Y = 6, there is no S such that X_N = 6, so output -1.
For the third query with Y = 7, both S = 6 and S = 7 result in X_N = 7, so the smallest S is 6.
Sample Input 2
10 1 310214852498133736 505276263682091678 273987911350501637 317207700241861186 878845869214220663 722059890180131902 597424946894933345 74297940232615233 969543184238991085 567669635596262039 760374976835769237 114205047640377864 975115657391620675 659404150340533368 514313531921108960 255579815636209538 1042405225853490071 891193105039531117 1032475514675208675 968262176137127595 2 942999108116930288 0 0
Sample Output 2
494185924924343867
Sample Input 3
10 5 20 19 18 17 16 15 14 13 12 11 11 12 13 14 15 16 17 18 19 20 2 8 0 0 1 6 100 200 2 12 0 0 1 10 32 662 2 100 0 0
Sample Output 3
8 103 -1
Sample Input 4
10 5 464468010685205695 652469322679259637 207750579744900414 551282264132274959 477385551779769369 457669217633528368 1124978699497706079 993018743713584412 347799342391956023 253839229959865684 43481420251962425 913779804742334221 721829783836314668 643562100144275666 148532568860178532 348780722732705987 905040003050597634 962374691997649953 160408954061784257 6313574278114070 2 942999108116930288 0 0 1 7 911289147093700219 315969390490734880 2 570806468566359262 0 0 1 5 865153057674787555 127079554510737035 2 71991180131886804 0 0
Sample Output 4
167766290121628811 833427363106128513 657636533261400102
配点 : 100 点
問題文
長さ N の非負整数列 A,B があります。はじめ、A=(A_1,A_2,\ldots,A_N),B=(B_1,B_2,\ldots,B_N) です。
Q 個のクエリが与えられるので、与えられた順に処理してください。
各クエリは次の 2 種類のどちらかです。
- タイプ 1 :
1 i a bの形式で与えられる。A_i の値を a に、B_i の値を b に変更する。 - タイプ 2 :
2 Y 0 0の形式で与えられる。次の問題を解く。非負整数 S に対し、非負整数列 X = (X_0, X_1, \dots, X_N) を次の漸化式で定義します。
- X_0 = S
- 各 1 \le i \le N について、X_i = \begin{cases} X_{i - 1} \oplus A_i & \text{if } X_{i - 1} \equiv 1 \pmod{2} \\ X_{i - 1} \oplus B_i & \text{if } X_{i - 1} \equiv 0 \pmod{2} \end{cases}
適切に非負整数 S を設定したとき X_N=Y とすることができるか判定し、可能な場合は、X_N=Y となるような S の最小値を出力してください。
X_N=Y となるような S が存在しない場合は、-1を出力してください。
制約
- 入力はすべて整数
- 1 \le N \le 2 \times 10^5
- 1 \le Q \le 2 \times 10^5
- 0 \le A_i,B_i < 2^{60} \ (1 \le i \le N)
- タイプ 1 のクエリにおいて、1 \le i \le N , 0 \le a ,b < 2^{60}
- タイプ 2 のクエリにおいて、0 \le Y \lt 2^{60}
- タイプ 2 のクエリが 1 つ以上存在する
部分点
追加の制約 Q=1 を満たすデータセットに正解した場合は 30 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N Q
A_1 A_2 \ldots A_N
B_1 B_2 \ldots B_N
\mathrm{query}_1
\vdots
\mathrm{query}_Q
ただし、\mathrm{query}_i は i 番目のクエリであり、以下のいずれかの形式で与えられる。
1 i a b
2 Y 0 0
出力
タイプ 2 のクエリの個数を q として、q 行出力せよ。i 行目には i 個目のタイプ 2 のクエリに対する答えを出力せよ。
入力例 1
1 3 0 1 2 5 0 0 2 6 0 0 2 7 0 0
出力例 1
4 -1 6
A = (0),\ B = (1) であるので、S が奇数なら X_N = S、S が偶数なら X_N = S \oplus 1 となります。
1 個目のクエリでは、Y = 5 です。S が 4 または 5 であれば X_N = 5 となるので、最小値の 4 を出力します。
2 個目のクエリでは、Y = 6 です。X_N = 6 となるような S は存在しないので、-1 を出力します。
3 個目のクエリでは、Y = 7 です。S が 6 または 7 であれば X_N = 7 となるので、最小値の 6 を出力します。
入力例 2
10 1 310214852498133736 505276263682091678 273987911350501637 317207700241861186 878845869214220663 722059890180131902 597424946894933345 74297940232615233 969543184238991085 567669635596262039 760374976835769237 114205047640377864 975115657391620675 659404150340533368 514313531921108960 255579815636209538 1042405225853490071 891193105039531117 1032475514675208675 968262176137127595 2 942999108116930288 0 0
出力例 2
494185924924343867
入力例 3
10 5 20 19 18 17 16 15 14 13 12 11 11 12 13 14 15 16 17 18 19 20 2 8 0 0 1 6 100 200 2 12 0 0 1 10 32 662 2 100 0 0
出力例 3
8 103 -1
入力例 4
10 5 464468010685205695 652469322679259637 207750579744900414 551282264132274959 477385551779769369 457669217633528368 1124978699497706079 993018743713584412 347799342391956023 253839229959865684 43481420251962425 913779804742334221 721829783836314668 643562100144275666 148532568860178532 348780722732705987 905040003050597634 962374691997649953 160408954061784257 6313574278114070 2 942999108116930288 0 0 1 7 911289147093700219 315969390490734880 2 570806468566359262 0 0 1 5 865153057674787555 127079554510737035 2 71991180131886804 0 0
出力例 4
167766290121628811 833427363106128513 657636533261400102
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
On the xy-plane, there are N points labeled 1, 2, \dots, N. The coordinates of point i (1 \le i \le N) are (X_i, Y_i).
There is a robot at the origin of this plane. Your task is to control the robot to visit all the points 1, 2, \dots, N in this order.
The robot has a string variable S, which is initially an empty string.
You can move the robot using the following four types of operations:
- Operation 1: Increase the robot's x coordinate by 1 and append
Xto the end of S. This operation costs 1. - Operation 2: Increase the robot's y coordinate by 1 and append
Yto the end of S. This operation costs 1. - Operation 3: Decrease the robot's x coordinate by 1 and remove the last character of S. This operation can only be performed if the last character of S is
X. This operation costs 0. - Operation 4: Decrease the robot's y coordinate by 1 and remove the last character of S. This operation can only be performed if the last character of S is
Y. This operation costs 0.
Find the minimum cost required for the robot to visit all points 1, 2, \dots, N in this order.
Constraints
- All input values are integers.
- 1 \le N \le 500
- 0 \le X_i, Y_i \le 10^9
Input
The input is given from Standard Input in the following format:
N X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
Output
Output the minimum cost required for the robot to visit all points in order.
Sample Input 1
2 3 3 1 2
Sample Output 1
6
By performing Operation 1 once, Operation 2 three times, and Operation 1 twice, you can reach point 1.
Then, by performing Operation 3 twice and Operation 4 once, you can reach point 2.
The total cost of this sequence of operations is the sum of the number of times Operations 1 and 2 are performed, which is 6.
Sample Input 2
3 2 2 3 3 1 3
Sample Output 2
7
配点 : 100 点
問題文
xy 平面上に 1, 2, \dots, N の番号が付けられた N 個の点があります。点 i (1 \le i \le N) の座標は (X_i, Y_i) です。
この平面上の原点にロボットがあります。あなたはこのロボットを操縦して、点 1, 2, \dots, N を この順にすべて 訪れなければなりません。
ロボットは文字列変数 S を持っています。はじめ、S は空文字列です。
あなたは以下の 4 種類の操作でロボットを動かすことができます。
- 操作 1 : ロボットの x 座標を 1 増やし、S の末尾に
Xを追加する。この操作には 1 のコストがかかる。 - 操作 2 : ロボットの y 座標を 1 増やし、S の末尾に
Yを追加する。この操作には 1 のコストがかかる。 - 操作 3 : ロボットの x 座標を 1 減らし、S の末尾の文字を削除する。この操作は S の末尾の文字が
Xであるときのみ行える。この操作にコストはかからない。 - 操作 4 : ロボットの y 座標を 1 減らし、S の末尾の文字を削除する。この操作は S の末尾の文字が
Yであるときのみ行える。この操作にコストはかからない。
点 1, 2, \dots, N をこの順に訪れるのにかかるコストの最小値を求めてください。
制約
- 入力はすべて整数
- 1 \le N \le 500
- 0 \le X_i, Y_i \le 10^9
入力
入力は以下の形式で標準入力から与えられる。
N X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
出力
ロボットが点 1, 2, \dots, N をこの順に訪れるのにかかるコストの最小値を出力せよ。
入力例 1
2 3 3 1 2
出力例 1
6
操作 1 を 1 回、操作 2 を 3 回、操作 1 を 2 回することで、点 1 を訪れることができ、 続けて、操作 3 を 2 回、操作 4 を 1 回することで、点 2 を訪れることができます。
上記の一連の操作のコストは、操作 1, 2 を行った回数の合計である 6 になります。
入力例 2
3 2 2 3 3 1 3
出力例 2
7
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given a string S, T of length N consisting of only uppercase English letters. You can perform the following operation 0 or more times:
- If there exists a substring of S such that
TIOT, choose one and replace it withISCT. (More precisely, if there exists 1 \le i \le N-3 such that S_{i}={}T, S_{i+1}={}I, S_{i+2}={}O, S_{i+3}={}T, choose one and replace it with S_{i}={}I, S_{i+1}={}S, S_{i+2}={}C, S_{i+3}={}T.)
Can you make S equal to T by performing the operation?
You have Q test cases to answer.
Constraints
- 1 \leq Q \leq 5 \times 10^4
- 4 \le N \le 2 \times 10^5
- S and T are strings of length N consisting of uppercase English letters.
- The sum of N across the test cases is at most 2 \times 10^5.
Input
The input is given in the following format:
Q
{case}_1
{case}_2
\vdots
{case}_Q
Each test cases is given in the following format:
N S T
Output
Print Q lines. On the i-th line, print the answer to the i-th test case as either Yes or No.
Sample Input 1
3 10 ETIOTROPIC EISCTROPIC 6 BTIEOT BISECT 10 TIOTIOTIOT TIOISCISCT
Sample Output 1
Yes No Yes
For the first test case, you can match ETIOTROPIC to EISCTROPIC by performing the operation once as follows:
- The substring from the 2 nd to 5 th characters in
ETIOTROPICisTIOT, so replace it withISCT.
For the second test case, you cannot match two strings through the operation.
配点 : 100 点
問題文
英大文字のみからなる長さ N の文字列 S, T が与えられます。あなたは S に次の操作を 0 回以上行うことができます。
- S の連続部分文字列が
TIOTである部分が存在すれば一つ選ぶ。その部分をISCTに置換する。(より正確には、1 \leq i \leq N-3 を満たす整数 i であって S_{i}={}T, S_{i+1}={}I, S_{i+2}={}O, S_{i+3}={}Tを満たすものが存在するなら一つ選び、S_{i}={}I, S_{i+1}={}S, S_{i+2}={}C, S_{i+3}={}Tに置換する。)
操作によって S を T に一致させることはできますか?
Q 個のテストケースが与えられるので、それぞれについて答えてください。
制約
- 1 \leq Q \leq 5 \times 10^4
- 4 \leq N \leq 2 \times 10^5
- S,T は英大文字からなる長さ N の文字列
- ひとつの入力について、含まれるテストケースの N の総和は 2 \times 10^5 を超えない
入力
入力は以下の形式で与えられる。
Q
{case}_1
{case}_2
\vdots
{case}_Q
各テストケースは以下の形式で与えられる。
N S T
出力
全体で Q 行出力せよ。 i 行目には i 個目のテストケースに対する答えを Yes または No で出力せよ。
入力例 1
3 10 ETIOTROPIC EISCTROPIC 6 BTIEOT BISECT 10 TIOTIOTIOT TIOISCISCT
出力例 1
Yes No Yes
1 個目のテストケースでは次のように操作を 1 回行うことで ETIOTROPIC を EISCTROPIC に一致させることができます。
ETIOTROPICの 2 文字目から 5 文字目がTIOTであるので、この部分をISCTに置き換える。
一方 2 個目のテストケースでは操作によって 2 つの文字列を一致させることはできません。
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given a rooted tree with N vertices. The vertices are numbered from 1 to N, with vertex 1 being the root. The i-th edge connects vertex A_i and vertex B_i.
Assign a color to each vertex such that the following condition is satisfied:
- Let the color of vertex i be c_i. For any three distinct vertices u, v, and w, if w = \mathrm{lca}(u, v) and c_u = c_v, then c_u \neq c_w.
Find the minimum possible number of distinct colors used.
Here, \mathrm{lca}(u, v) denotes the lowest common ancestor of vertices u and v.
Constraints
- All input values are integers.
- 3 \leq N \leq 2 \times 10^5
- 1 \leq A_i, B_i \leq N
- The input graph is a tree.
Input
The input is given in the following format:
N
A_1 B_1
A_2 B_2
\vdots
A_{N-1} B_{N-1}
Output
Print the minimum number of distinct colors required.
Sample Input 1
8 1 2 1 3 2 4 2 5 3 6 3 7 6 8
Sample Output 1
3
For example, the coloring shown below satisfies the given conditions.
Since there is no way to satisfy the conditions using two or fewer colors, the minimum number of colors needed is 3.
Sample Input 2
4 1 2 2 3 3 4
Sample Output 2
1
配点 : 100 点
問題文
N 頂点からなる根付き木が与えられます。この木の頂点には 1 から N までの番号が振られており、頂点 1 が根です。i 番目の辺は、頂点 A_i と頂点 B_i を結んでいます。
木の各頂点に対し、次の条件を満たすように色を塗ります。
- 頂点 i の色を c_i とする。任意の相異なる 3 頂点 u, v, w について、「 w = \mathrm{lca}(u, v) かつ c_u = c_v ならば c_u \neq c_w 」 が成り立つ。
このとき、使用した色の種類数としてありうる最小値を求めてください。
ここで、\mathrm{lca}(u, v) は頂点 u と頂点 v の最小共通祖先を表します。
制約
- 入力はすべて整数
- 3 ≤ N ≤ 2 \times 10^5
- 1 ≤ A_i, B_i ≤ N
- 入力されるグラフは木
入力
入力は以下の形式で与えられる。
N
A_1 B_1
A_2 B_2
\vdots
A_{N-1} B_{N-1}
出力
答えを出力せよ。
入力例 1
8 1 2 1 3 2 4 2 5 3 6 3 7 6 8
出力例 1
3
例えば、下図のように色を塗ると、与えられた条件を満たします。
2 色以下で条件を満たすように頂点を塗り分ける方法は存在しないため、使う色の種類数の最小値は 3 となります。
入力例 2
4 1 2 2 3 3 4
出力例 2
1
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Let’s consider abbreviating a programming contest held once a year using a sequence of four uppercase English letters. This year's abbreviation is
TTPC!
Problem Statement
The abbreviation-deciding machine \mathrm{M} for a programming contest has a string S of length N consisting of uppercase English letters and an integer sequence A = (A_1, A_2, \dots, A_N) of length N.
Additionally, machine \mathrm{M} has four cursors numbered from 1 to 4 for pointing at characters in S. Initially, for each i = 1, 2, 3, 4, cursor i points to the x_i-th character of S.
The machine \mathrm{M} has two buttons: the Abbreviation Button and the Update Button. Pressing these buttons triggers the following actions:
- Abbreviation Button: Machine \mathrm{M} outputs a string of length 4 formed by concatenating the characters pointed to by cursors 1, 2, 3, 4 in this order.
- Update Button: For each i = 1, 2, 3, 4, the following happens:
- Let y be the current position of cursor i. Cursor i moves from the y-th character of S to the A_y-th character of S.
This year's programming contest abbreviation was determined by pressing the Abbreviation Button, resulting in TTPC. Here, "this year" refers to 0 years from now.
Starting from next year, the abbreviation for the programming contest each year will be obtained through the following steps:
- Press the update button.
- Press the abbreviation button to determine the abbreviation.
How many years from now will the abbreviation return to TTPC for the last time? Will the end of TTPC come?
Constraints
- N, A_i, x_1, x_2, x_3, x_4 are integers.
- 3 \leq N \leq 50
- S is a string of length N consisting of uppercase English letters.
- 1 \leq A_i \leq N\ (1 \leq i \leq N)
- 1 \leq x_1, x_2, x_3, x_4 \leq N
- S_{x_1} = {}
T - S_{x_2} = {}
T - S_{x_3} = {}
P - S_{x_4} = {}
C
Input
The input is given in the following format:
N S A_1 A_2 \dots A_N x_1 x_2 x_3 x_4
Output
Output a non-negative integer k satisfying the following conditions. If such a k does not exist, output NeverEnds instead.
- The abbreviation becomes
TTPCk years from now. - For any integer l > k, the abbreviation does not become
TTPCl years from now.
Sample Input 1
5 TTTPC 2 3 4 4 5 1 2 4 5
Sample Output 1
1
- 0 years from now, the abbreviation is
TTPC, and the cursor positions are (1,2,4,5). - 1 year from now, the abbreviation is
TTPC, and the cursor positions are (2,3,4,5). - 2 years from now, the abbreviation is
TPPC, and the cursor positions are (3,4,4,5). - 3 years from now, the abbreviation is
PPPC, and the cursor positions are (4,4,4,5).
The last time the abbreviation becomes TTPC is 1 year from now.
Sample Input 2
4 TTPC 2 3 4 1 1 2 3 4
Sample Output 2
NeverEnds
The abbreviation becomes TTPC at years 0, 4, 8, 12, \dots and so on. TTPC never ends.
Sample Input 3
6 TTPCZT 5 3 2 6 4 4 1 2 3 4
Sample Output 3
0
配点 : 100 点
1 年に 1 回行われるプログラミングコンテストの略称を、英大文字を 4 つ並べて得ることを考えましょう。今年の略称は
TTPCです!
問題文
プログラミングコンテストの略称決めマシーン \mathrm{M} は、英大文字からなる長さ N の文字列 S と長さ N の整数列 A = (A_1, A_2, \dots, A_N) を持っています。 また、マシーン \mathrm{M} は S の中の文字を指し示すためのカーソルを 4 つ持っており、それぞれ 1 から 4 までの番号がついています。 はじめ、i = 1, 2, 3, 4 のそれぞれについて、カーソル i は S の x_i 文字目を指しています。
\mathrm{M} には 2 つのボタン 略称決めボタン と 更新ボタン がついています。このボタンを押すと、それぞれ以下のことが起こります。
- 略称決めボタン: マシーン \mathrm{M} は、カーソル 1, 2, 3, 4 が指している文字をこの順につなげた長さ 4 の文字列を出力する。
- 更新ボタン: i = 1, 2, 3, 4 のそれぞれについて以下が起こる。
- 現在カーソル i が指している文字を S の y 文字目とする。カーソル i が指す文字が、S の y 文字目から S の A_y 文字目に変わる。
略称決めボタンを押して得た文字列を今年のプログラミングコンテストの略称としたところ、TTPC に決まりました。ただし、今年とは今から 0 年後のことです。
来年以降毎年行われるプログラミングコンテストの略称は、次の手順で得ることにします。
- 更新ボタンを押す。
- 略称決めボタンを押して得た文字列を略称とする。
最後に略称が TTPC になるのは今から何年後のことでしょうか?それとも TTPC の終わりは来ないのでしょうか?
制約
- N,A_i,x_1,x_2,x_3,x_4 は整数
- 3\le N\le 50
- S は英大文字からなる長さ N の文字列
- 1\le A_i\le N\ (1\le i\le N)
- 1\le x_1,x_2,x_3,x_4\le N
- S_{x_1}={}
T - S_{x_2}={}
T - S_{x_3}={}
P - S_{x_4}={}
C
入力
入力は以下の形式で標準入力から与えられる。
N S A_1 A_2 \dots A_N x_1 x_2 x_3 x_4
出力
以下の条件を満たす非負整数 k を出力せよ。そのような k が存在しない場合は、代わりに NeverEnds と出力せよ。
- k 年後に略称が
TTPCとなる。 - k より大きい任意の整数 l について、l 年後の略称は
TTPCではない。
入力例 1
5 TTTPC 2 3 4 4 5 1 2 4 5
出力例 1
1
- 今から 0 年後の略称は
TTPCで、カーソルの位置は (1,2,4,5) です。 - 今から 1 年後の略称は
TTPCで、カーソルの位置は (2,3,4,5) です。 - 今から 2 年後の略称は
TPPCで、カーソルの位置は (3,4,4,5) です。 - 今から 3 年後の略称は
PPPCで、カーソルの位置は (4,4,4,5) です。
最後に略称が TTPC になるのは 1 年後です。
入力例 2
4 TTPC 2 3 4 1 1 2 3 4
出力例 2
NeverEnds
0,4,8,12,\dots 年後に略称が TTPC となります。TTPC は終わりません。
入力例 3
6 TTPCZT 5 3 2 6 4 4 1 2 3 4
出力例 3
0
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
This is an interactive problem, where your program interacts with the judge system via Standard Input and Output.
You are given integers N, K, and Q.
The judge holds a hidden permutation (a_1, a_2, \dots, a_N) of (1, 2, \dots, N).
You may ask up to Q queries to the judge, where each query is as follows:
- Choose a subset S from \lbrace 1, 2, \dots, N \rbrace. The judge will return the number of distinct pairs (i, j) such that i < j and |a_i - a_j| \leq K where i, j \in S.
Let x be the index t where a_t = 1, and y be the index t where a_t = N. Your task is to identify the set \lbrace x, y \rbrace. (You do not need to distinguish which is x and which is y.)
The judge is non-adaptive, that means the permutation (a_1, a_2, \dots, a_N) is fixed before any interaction begins.
Constraints
- All input values are integers.
- N = 20000
- 1 \leq K \leq 10
- Q = 30(K + 1)
Partial Score
30 points will be awarded for passing the test set satisfying the additional constraint K = 10.
Input and Output
This is an interactive problem.
First, read integers N, K, and Q from the Standard Input:
N K Q
Then, repeat the following process until you identify the set \lbrace x, y \rbrace:
For a query, output the following format to the Standard Output:
? s_1s_2 \dots s_N
Here, s_1 s_2 \dots s_N is a binary string of length N representing the subset S, where s_i = {}1 if i \in S, and s_i = {}0 otherwise.
The response to your query will be provided in the Standard Input in the following format:
T
Here, T is the answer to the query, representing the number of distinct pairs (i, j) such that i < j and |a_i - a_j| \leq K where i, j \in S.
Once you identify the set \lbrace x, y \rbrace, output the two elements in the following format (order does not matter) and terminate your program immediately:
! x y
Notes
- Print a newline and flush Standard Output at the end of each message. Otherwise, you may get a TLE verdict.
- If your query format is invalid or you exceed the number of queries, the judge will respond with T = -1. If you receive this response, you should immediately terminate your program. Otherwise, you may get a TLE verdict.
- Beware that unnecessary newlines are considered as malformed.
Sample Interaction
The following is a sample interaction for N = 5, K = 2, Q = 90. Note that this example does not meet the constraints and will not appear in the test cases.
| Input | Output | Explanation |
|---|---|---|
| The judge holds the permutation (3, 5, 2, 1, 4). | ||
5 2 90 |
First, integers N, K, and Q are provided. | |
? 11000 |
You query with S = \lbrace 1, 2 \rbrace. | |
1 |
Only the pair (1, 2) satisfies the condition, so the judge responds with 1. |
|
? 10011 |
You query with S = \lbrace 1, 4, 5 \rbrace. | |
2 |
The pairs (1, 4) and (1, 5) satisfy the condition, so the judge responds with 2. |
|
! 2 4 |
You output \lbrace 2, 4 \rbrace as the answer. Since a_4 = 1 and a_2 = N, this output is correct. |
配点 : 100 点
問題文
この問題は インタラクティブな問題(あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題)です。
整数 N, K, Q が与えられます。 ジャッジシステムは (1, 2, \dots, N) の順列 (a_1, a_2, \dots, a_N) を隠し持っています。 あなたはジャッジに Q 回まで次のような質問をすることが出来ます。
- \lbrace 1, 2, \dots, N \rbrace の部分集合 S を選ぶ。S の異なる 2 元の組 (i,j) であって、 i<j かつ |a_i-a_j|\leq K であるような組の個数を聞く。
a_t=1 となるような t を x とし、 a_t=N となるような t を y とします。 集合 \lbrace x,y \rbrace を特定してください。(どちらが x でどちらが y かを特定する必要はありません。)
なお、ジャッジは適応的 (adaptive) ではなく、順列 (a_1, a_2, \dots, a_N) はやりとりの前から固定されています。
制約
- 入力はすべて整数
- N = 20000
- 1 \leq K \leq 10
- Q = 30(K + 1)
部分点
追加の制約 K = 10 を満たすデータセットに正解した場合は 30 点が与えられる。
入出力
この問題はインタラクティブな問題です。
最初に、整数 N,K,Q を標準入力から受け取ってください。
N K Q
次に、集合 \lbrace x, y \rbrace を特定できるまで質問を繰り返してください。
質問は、以下の形式で標準出力に出力してください。
? s_1s_2 \dots s_N
ここで、s_1 s_2 \dots s_N は部分集合 S を表す長さ N の文字列で、i \in S ならば s_i = {}1、i \notin S ならば s_i = {}0 としてください。
これに対する応答は、以下の形式で標準入力から与えられます。
T
ここで、T は質問に対する答えで、S の異なる 2 元の組 (i,j) であって、 i<j かつ |a_i-a_j|\leq K であるような組の個数を表します。
答えとなる集合 \lbrace x, y \rbrace を特定出来たら、特定した 2 つの要素を以下の形式で出力してください。(順番はどちらが先でも構いません。)その後、ただちにプログラムを終了してください。
! x y
注意点
- 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
- 質問の形式が間違っている場合、および、質問回数を超過した場合、ジャッジの応答は T = -1 となります。これを受け取った場合、ただちにプログラムを終了してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
- 余計な改行は不正なフォーマットの出力とみなされることに注意してください。
入出力例
以下は N = 5, K = 2, Q = 90 の場合の入出力例です。この例は入力の制約を満たさないので、テストケースには含まれないことに注意してください。
| 入力 | 出力 | 説明 |
|---|---|---|
| ジャッジは順列 (3, 5, 2, 1, 4) を隠し持っています。 | ||
5 2 90 |
まず整数 N,K,Q が与えられます。 | |
? 11000 |
S = \lbrace 1, 2 \rbrace として質問を行います。 | |
1 |
組 (1, 2) のみが条件を満たすので、標準入力に 1 が与えられます。 |
|
? 10011 |
S = \lbrace 1, 4, 5 \rbrace として質問を行います。 | |
2 |
(1, 4) と (1, 5) の 2 組が条件を満たすので、標準入力に 2 が与えられます。 |
|
! 2 4 |
答えとして \lbrace 2, 4 \rbrace を出力します。a_4 = 1 かつ a_2 = N であるので、この出力は正解です。 |
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given positive integers H and W. You aim to draw an H-row by W-column grid on the coordinate plane using several "U-shapes."
To draw one U-shape, perform the following operation:
- Choose integers 1 \le x \le H and 1 \le y \le W.
- From the following four line segments, select any three distinct ones:
- The line segment connecting (x-1, y-1) and (x-1, y)
- The line segment connecting (x-1, y-1) and (x, y-1)
- The line segment connecting (x, y) and (x-1, y)
- The line segment connecting (x, y) and (x, y-1)
- Draw the selected three line segments on the coordinate plane.
However, the line segments you draw must not share any points (other than endpoints) with any line segments drawn previously.
Is it possible to draw all the length-1 line segments connecting grid points with 0 \le x \le H and 0 \le y \le W by repeating this operation? If possible, provide an example.
Constraints
- All input values are integers.
- 1 \le H, W \le 1000
Partial Score
10 points will be awarded for passing the testset satisfying the additional constraint H,W\le 5.
Input
The input is given from Standard Input in the following format:
H W
Output
If it is impossible to draw the grid by repeating the operation, output No.
If it is possible, output such an operation sequence in the following format:
Yes S_1 \vdots S_H
Here, S_1, \dots, S_H are strings of length W, and the j-th character of S_i (1 \le i \le H, 1 \le j \le W) is defined as follows:
- If there is no operation with (x, y) = (i, j), the j-th character of S_i is
.. - Otherwise, there is exactly one operation with (x, y) = (i, j). In that operation:
- If the three selected line segments are those excluding "the line segment connecting (x-1, y-1) and (x-1, y)," then the j-th character of S_i is
v. - If the three selected line segments are those excluding "the line segment connecting (x-1, y-1) and (x, y-1)," then the j-th character of S_i is
>. - If the three selected line segments are those excluding "the line segment connecting (x, y) and (x-1, y)," then the j-th character of S_i is
<. - If the three selected line segments are those excluding "the line segment connecting (x, y) and (x, y-1)," then the j-th character of S_i is
^.
- If the three selected line segments are those excluding "the line segment connecting (x-1, y-1) and (x-1, y)," then the j-th character of S_i is
Note that the judge is case-insensitive for Yes and No.
Refer to the sample inputs and the visualizer for further clarification.
Visualizer
You can use the visualizer via the following link:
https://img.atcoder.jp/ttpc2024_1/grid_construction_visualizer_9cdb863ae8b195d0a47d8d6e2c9e05cd.html
Sample Input 1
3 3
Sample Output 1
Yes <<^ v.^ v>>
As shown in the figure, you can draw a 3 \times 3 grid by drawing U-shapes. Note that no U-shape is drawn at the location corresponding to the center cell. (For clarity, the U-shapes are colored, but this is irrelevant to the problem.)
Sample Input 2
4 4
Sample Output 2
No
Sample Input 3
4 5
Sample Output 3
No
配点 : 100 点
問題文
正整数 H,W が与えられます。あなたは座標平面にいくつかの「コの字」を用いて H 行 W 列のグリッドを描こうとしています。
1 つのコの字を描くには、次の操作を行います。
- 1\le x\le H, 1\le y\le W なる整数 x,y を選ぶ。
- 次の 4 本の線分のうち、異なる 3 本を選ぶ。
- (x-1,y-1) と (x-1,y) を端点に持つ線分
- (x-1,y-1) と (x,y-1) を端点に持つ線分
- (x,y) と (x-1,y) を端点に持つ線分
- (x,y) と (x,y-1) を端点に持つ線分
- 選んだ 3 本の線分を座標平面に描く。
ただし、描いた線分は、それまでに描いた線分と端点以外で共有点を持ってはいけません。
0 \le x \le H, 0 \le y \le W の範囲にある格子点同士を結ぶ長さ 1 の線分すべてを、この操作を繰り返すことで描くことは可能でしょうか?可能である場合は一例を示してください。
制約
- 入力はすべて整数
- 1\le H,W\le 1000
部分点
追加の制約 H, W \le 5 を満たすデータセットに正解した場合は 10 点が与えられる。
入力
入力は以下の形式で与えられる。
H W
出力
操作を繰り返してグリッドを描くことが不可能である場合は、No を出力せよ。
操作を繰り返してグリッドを描くことが可能である場合は、そのような操作列を以下の形式で出力せよ。
Yes S_1 \vdots S_H
ここで、S_1, \dots, S_H はそれぞれ長さ W の文字列であり、S_i の j 文字目 (1 ≤ i ≤ H,\ 1 ≤ j ≤ W) は次のように定義される。
- (x, y) = (i, j) であるような操作が存在しない場合、S_i の j 文字目は
.である。 - そうでない場合、(x, y) = (i, j) であるような操作はちょうど 1 回存在する。その操作において、
- 「(x-1,y-1) と (x-1,y) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
vである。 - 「(x-1,y-1) と (x,y-1) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
>である。 - 「(x,y) と (x-1,y) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
<である。 - 「(x,y) と (x,y-1) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
^である。
- 「(x-1,y-1) と (x-1,y) を端点に持つ線分」以外 の 3 本を選んだ場合、S_i の j 文字目は
なお、ジャッジは Yes と No の大文字・小文字を区別しない。
入出力例やビジュアライザも参考にせよ。
ビジュアライザ
以下のリンクからビジュアライザを利用できます。
https://img.atcoder.jp/ttpc2024_1/grid_construction_visualizer_9cdb863ae8b195d0a47d8d6e2c9e05cd.html
入力例 1
3 3
出力例 1
Yes <<^ v.^ v>>
図のようにコの字を描くことで、 3 \times 3 のグリッドを描くことができます。中央のマスに対応する場所にはコの字を描いていないことに注意してください。(見やすさのため、コの字に色をつけていますが、問題には関係ありません。)
入力例 2
4 4
出力例 2
No
入力例 3
4 5
出力例 3
No
Time Limit: 8 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given a sequence A = (A_1, A_2, \cdots, A_N) of length N, consisting of 0, 1, and -1.
There are 2^q ways to replace all -1s in A with either 0 or 1, where q is the number of -1s in A. Among these, for all sequences that contain both 0 and 1, calculate the sum of the answers to the following problem modulo 998244353:
Let \alpha and \beta be the number of 0s and 1s in A, respectively.
Also, let X = (X_0, X_1, \cdots, X_{\alpha-1}) be the sequence of indices of A_i = 0, arranged in increasing order, and let Y = (Y_0, Y_1, \cdots, Y_{\beta-1}) be the sequence of indices of A_i = 1, arranged in increasing order (note that the indices of X and Y start from 0).
Calculate the value of the above expression.\displaystyle\sum_{i=0}^{\mathrm{LCM}(\alpha, \beta)-1} |X_{(i \bmod \alpha)} - Y_{(i \bmod \beta)}|
Here, \mathrm{LCM}(x, y) represents the least common multiple of x and y, and x \bmod y denotes the remainder when x is divided by y.
Constraints
- All input values are integers.
- 2 \leq N \leq 2250
- Each A_i is either 0, 1, or -1 (i = 1, 2, \cdots, N).
Partial Score
- 30 points will be awarded for passing the test set satisfying the additional constraint N \leq 100.
Input
The input is given in the following format:
N A_1 A_2 \cdots A_N
Output
Output the answer.
Sample Input 1
4 1 1 -1 -1
Sample Output 1
14
For A = (1, 1, 0, 0), |3 - 1| + |4 - 2| = 4.
For A = (1, 1, 0, 1), |3 - 1| + |3 - 2| + |3 - 4| = 4.
For A = (1, 1, 1, 0), |4 - 1| + |4 - 2| + |4 - 3| = 6.
Thus, the answer is 4 + 4 + 6 = 14.
Sample Input 2
3 0 0 0
Sample Output 2
0
Since it is not possible to form a sequence containing both 0 and 1, the answer is 0.
Sample Input 3
10 -1 -1 0 -1 -1 1 -1 -1 -1 -1
Sample Output 3
10152
配点 : 100 点
問題文
0, 1, -1 からなる長さ N の数列 A=(A_1,A_2,\cdots,A_N) が与えられます。
A に含まれる −1 をすべて 0 または 1 で置き換える方法は、A に含まれる −1 の個数を q とすると 2^q 通りあります。このうち A に 0 と 1 を両方含むものすべてに対して、以下の問題を解いたときの答えの和を 998244353 で割ったあまりを求めてください。
A に含まれる 0, 1 の個数をそれぞれ \alpha, \beta とします。
また、 A_i=0 となるような i を小さい順に並べた数列を X=(X_0,X_1,\cdots,X_{\alpha-1})とし、 A_i=1 となるような i を小さい順に並べた数列を Y=(Y_0,Y_1,\cdots,Y_{\beta-1}) とします( X と Y はともに添え字が 0 から始まることに注意してください)。の値を求めてください。\displaystyle\sum_{i=0}^{\mathrm{LCM}(\alpha,\beta)-1}|X_{(i\bmod \alpha)}-Y_{(i\bmod \beta)}|
ただし、 \mathrm{LCM}(x,y) は x と y の最小公倍数、 x\bmod y は x を y で割ったあまりを表すものとします。
制約
- 入力はすべて整数
- 2\leq N\leq 2250
- A_i は 0, 1, -1 のいずれか (i=1,2,\cdots,N)
部分点
- 追加の制約 N\leq 100 を満たすデータセットに正解した場合は 30 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \cdots A_N
出力
答えを出力せよ。
入力例 1
4 1 1 -1 -1
出力例 1
14
A=(1,1,0,0) のとき |3-1|+|4-2|=4
A=(1,1,0,1) のとき |3-1|+|3-2|+|3-4|=4
A=(1,1,1,0) のとき |4-1|+|4-2|+|4-3|=6
よって、答えは 4+4+6=14 となります。
入力例 2
3 0 0 0
出力例 2
0
0 と 1 を両方含むような数列を作れないため、答えは 0 となります。
入力例 3
10 -1 -1 0 -1 -1 1 -1 -1 -1 -1
出力例 3
10152
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
In this problem, when we refer to a "permutation of length K", we mean a permutation of (0, 1, \dots, K - 1). Also, we denote the k-th element (0-based) of a sequence X as X[k].
You are given a permutation P of length L, and L permutations of length B, denoted as V_{0}, V_{1}, \dots, V_{L - 1}.
We define a sequence A of length B^L as follows:
For each 0 ≤ n < B^L, when n is represented as an L-digit number in base B, let N[i] be the value at the B^i place (0 ≤ i < L). Then,\displaystyle A[n] = \sum_{i=0}^{L-1} V_i[N[i]] \cdot B^{P[i]}
Find the inversion number of the sequence A modulo 998244353.
Constraints
- All input values are integers
- 1 \leq L
- 2 \leq B
- L \times (B + 1) \leq 5 \times 10^{5}
- P is a permutation of length L
- For each 0 \leq i < L, V_{i} is a permutation of length B
Input
Input is given from standard input in the following format:
L B
P[0] P[1] \cdots P[L - 1]
V_{0}[0] V_{0}[1] \cdots V_{0}[B - 1]
\vdots
V_{L - 1}[0] V_{L - 1}[1] \cdots V_{L - 1}[B - 1]
Output
Print the answer.
Sample Input 1
3 2 2 0 1 1 0 1 0 0 1
Sample Output 1
14
For example, when n = 5, since N = (1, 0, 1), we have A[5] = V_{0}[1] \cdot 2^{P[0]} + V_{1}[0] \cdot 2^{P[1]} + V_{2}[1] \cdot 2^{P[2]}=3.
By calculating similarly, we get A = (5, 1, 4, 0, 7, 3, 6, 2). The inversion count of A is 14, so output 14.
Sample Input 2
2 4 1 0 2 0 3 1 1 2 3 0
Sample Output 2
60
A = (9, 1, 13, 5, 10, 2, 14, 6, 11, 3, 15, 7, 8, 0, 12, 4). The inversion count of A is 60, so output 60.
Sample Input 3
9 10 2 5 7 3 8 1 4 6 0 9 2 4 0 1 6 7 3 5 8 4 1 6 7 8 0 5 9 2 3 1 9 2 4 6 8 5 7 0 3 9 0 8 2 5 1 6 7 3 4 1 6 0 7 3 9 2 4 5 8 4 5 2 9 1 6 7 3 0 8 7 0 5 6 1 9 2 4 3 8 3 2 1 6 7 0 8 9 4 5 9 2 4 3 5 8 0 6 7 1
Sample Output 3
138876070
Output the answer modulo 998244353.
配点 : 100 点
問題文
この問題で「長さ K の順列」と言った際は「(0, 1, \dots, K - 1) の順列」を指すものとします。また、数列 X の k 番目の要素(最初の要素を 0 番目とする)を X[k] と表すこととします。
長さ L の順列 P と、L 個の長さ B の順列 V_{0}, V_{1}, \dots, V_{L - 1} が与えられます。
長さ B^L の数列 A を以下のように定義します。
各 0 ≤ n < B^L に対し、n を B 進 L 桁で表した際の B^i の位 (0 ≤ i < L) の値を N[i] とすると、\displaystyle A[n] = \sum_{i=0}^{L-1} V_i[N[i]] \cdot B^{P[i]}である。
数列 A の転倒数を 998244353 で割ったあまりを求めてください。
制約
- 入力はすべて整数
- 1 \leq L
- 2 \leq B
- L \times (B + 1) \leq 5 \times 10^{5}
- P は長さ L の順列である
- 各 0 \leq i < L について、V_{i} は長さ B の順列である
入力
入力は以下の形式で標準入力から与えられる。
L B
P[0] P[1] \cdots P[L - 1]
V_{0}[0] V_{0}[1] \cdots V_{0}[B - 1]
\vdots
V_{L - 1}[0] V_{L - 1}[1] \cdots V_{L - 1}[B - 1]
出力
答えを出力せよ。
入力例 1
3 2 2 0 1 1 0 1 0 0 1
出力例 1
14
例えば n = 5 のとき、N = (1, 0, 1) であるので、A[5] = V_{0}[1] \cdot 2^{P[0]} + V_{1}[0] \cdot 2^{P[1]} + V_{2}[1] \cdot 2^{P[2]}=3 です。
同様にして計算すると、A = (5, 1, 4, 0, 7, 3, 6, 2) となります。A の転倒数は 14 であるので、14 を出力します。
入力例 2
2 4 1 0 2 0 3 1 1 2 3 0
出力例 2
60
A = (9, 1, 13, 5, 10, 2, 14, 6, 11, 3, 15, 7, 8, 0, 12, 4) です。A の転倒数は 60 であるので、60 を出力します。
入力例 3
9 10 2 5 7 3 8 1 4 6 0 9 2 4 0 1 6 7 3 5 8 4 1 6 7 8 0 5 9 2 3 1 9 2 4 6 8 5 7 0 3 9 0 8 2 5 1 6 7 3 4 1 6 0 7 3 9 2 4 5 8 4 5 2 9 1 6 7 3 0 8 7 0 5 6 1 9 2 4 3 8 3 2 1 6 7 0 8 9 4 5 9 2 4 3 5 8 0 6 7 1
出力例 3
138876070
998244353 で割ったあまりを求めてください。
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
There are N \times M stones on a number line, with M colors labeled 1 through M, and N stones of each color. Here, N is an even number, and M is an odd number. Among the stones of color i, the j-th stone from the left (1 ≤ i ≤ M,\ 1 ≤ j ≤ N) is initially placed at the coordinate (j-1) \times M + i. Stones of the same color are indistinguishable.
You can perform the following operation up to (N+1) \times M times:
Pick two adjacent stones and move them, in the same order, to any unoccupied adjacent positions.
Specifically:
- Choose an integer x such that -10^9 \leq x \leq 10^9-1 and there are stones at both coordinates x and x+1. Let the stone at x be A and the stone at x+1 be B. Remove A and B from the number line.
- Choose an integer y such that -10^9 \leq y \leq 10^9-1 and there are no stones at both coordinates y and y+1. Place A at y and B at y+1.
Your goal is to rearrange the stones to satisfy the following two conditions:
- All stones are part of a single contiguous block. That is, there exists an integer n such that for all integers x satisfying n \leq x \leq n + NM - 1, there is exactly one stone at coordinate x.
- Additionally, the stones are sorted by color in ascending order. Specifically, among the stones of color i, the j-th stone from the left (1 ≤ i ≤ M,\ 1 ≤ j ≤ N) is at coordinate n + (i-1) \times N + (j-1).
Under the constraints of this problem, it can be shown that the goal is always achievable. Output one valid sequence of operations to achieve the goal. You do not need to minimize the number of operations.
Constraints
- 2 \leq N \leq 1000
- 3 \leq M \leq 999
- N is even
- M is odd
Input
The input is given in the following format:
N M
Output
Output the solution in the following format:
K x_1 y_1 x_2 y_2 \vdots x_K y_K
Here, K is the number of operations performed, and x_k, y_k\ (1 \leq k \leq K) represent the values of x and y chosen in the k-th operation.
The output must satisfy the following constraints:
- 0 \leq K \leq (N+1) \times M
- -10^9 \leq x_k, y_k \leq 10^9-1\ (1 \leq k \leq K)
If there are multiple valid solutions, output any one of them.
Sample Input 1
4 3
Sample Output 1
13 3 13 10 3 12 10 6 12 4 6 1 4 13 14 14 14 14 999999999 999999999 -1000000000 9 13 5 9 -1000000000 5
Initially, the stones are placed as follows (. indicates an unoccupied position). The coordinate of the leftmost . is 0, and the coordinate of the rightmost . is 15.
.123123123123...
After the first three operations, the stone arrangement changes as follows:
.123123123123... ↓ .12..2312312331. ↓ .121223123..331. ↓ .12122312333..1.
Finally, the stones are rearranged as follows:
...111122223333.
This arrangement satisfies the conditions of being a single contiguous block and sorted by color. Additionally, the number of operations is at most (N + 1) \times M = 15, so this output is valid.
配点 : 100 点
問題文
数直線上に色 1 から色 M までの M 色の石がそれぞれ N 個ずつ、合計 NM 個の石があります。ここで、N は 偶数 、M は 奇数 です。色 i の石のうち左から j 番目のもの (1 ≤ i ≤ M,\ 1 ≤ j ≤ N) は座標 (j-1) \times M + i に置かれています。同じ色の石同士には区別はありません。
あなたは以下の操作を (N+1)\times M 回まで行うことができます。
2 個並んでいる石を掴み取り、順番を変えずに空いている好きな場所に移す。
より正確には、以下の操作を行う。
- -10^9 ≤ x ≤ 10^9-1 を満たす整数 x であって、座標 x,x+1 の両方に石が置かれているようなものを選ぶ。座標 x に置かれている石を A 、座標 x+1 に置かれている石を B とする。A,B をいったん数直線上から取り除く。
- 次に、-10^9 ≤ y ≤ 10^9-1 を満たす整数 y であって、座標 y,y+1 の両方に石が置かれていないようなものを選ぶ。座標 y に A を、座標 y+1 に B をそれぞれ置く。
あなたの目標は、次の 2 つの条件を満たすように石を配置することです。
- 全ての石は連続した 1 つの塊になっている。すなわち、ある整数 n が存在して、n \le x \le n+NM-1 を満たすすべての整数 x に対して、座標 x に石がちょうど 1 個置かれている。
- さらに、石は色の昇順にソートされている。すなわち、色 i の石のうち左から j 番目のもの (1 ≤ i ≤ M,\ 1 ≤ j ≤ N) は座標 n + (i-1) \times N + (j-1) にある。
この問題の制約下で、目標は必ず達成可能であることが示せます。目標を達成する具体的な操作方法を 1 つ出力してください。操作回数を最小化する必要はないことに注意してください。
制約
- 2 \le N \le 1000
- 3 \le M \le 999
- N は偶数
- M は奇数
入力
入力は以下の形式で与えられる。
N M
出力
答えを以下の形式で出力せよ。
K x_1 y_1 x_2 y_2 \vdots x_K y_K
ここで、K は行う操作の回数であり、x_k, y_k\ (1 ≤ k ≤ K) は k 回目の操作において選ばれた x,y を表す。
出力は以下の制約を満たさなければならない。
- 0 \le K \le (N+1) \times M
- -10^9 \le x_k,y_k \le 10^9-1\ (1 ≤ k ≤ K)
条件を満たす解が複数存在する場合は、どれを出力しても正解とみなされる。
入力例 1
4 3
出力例 1
13 3 13 10 3 12 10 6 12 4 6 1 4 13 14 14 14 14 999999999 999999999 -1000000000 9 13 5 9 -1000000000 5
最初の状態では、以下のように石が置かれています。(. は石が置かれていないことを表します)。左端の . の座標は 0 、右端の . の座標は 15 です。
.123123123123...
最初の 3 回の操作により、石の配置は以下のように変化します。
.123123123123... ↓ .12..2312312331. ↓ .121223123..331. ↓ .12122312333..1.
最終的に、石の配置は以下のようになります。
...111122223333.
この配置は石が 1 つの塊になっていて、色の昇順にソートされています。操作回数も (N + 1) \times M = 15 回以下であるので、この出力は正解となります。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
N 頂点の木が与えられます。木の頂点には 1, 2, \dots, N の番号がついており、i 番目の辺 (1 ≤ i ≤ N-1) は頂点 u_i と頂点 v_i を結んでいます。
Alice と Bob は、頂点に自分の印をつけることを繰り返すゲームを行います。はじめ、どの頂点にも印はついていません。
まず、Alice が好きな頂点を選んで自分の印をつけます。次に、Bob から始めて交互に次の操作を行います。操作を行えなかった方の負けで、そうでない方の勝ちです。
- 次の条件を満たす頂点 v をひとつ選ぶ。
- 頂点 v には印がついていない。
- 頂点 v と辺で繋がれているある頂点 u が存在して、相手がつけた印がついている。
- 選んだ頂点 v に自分の印をつける。
両者が自身の勝ちを目指して最適に行動するとき、どちらが勝つかを求めてください。
制約
- 入力はすべて整数
- 1\le N\le 2\times 10^5
- 1\le u_i,v_i\le N
- 与えられるグラフは木である
入力
入力は以下の形式で標準入力から与えられる。
N
u_1 v_1
\vdots
u_{N-1} v_{N-1}
出力
Alice が勝つなら Alice を、Bob が勝つなら Bob を出力してください。
入力例 1
5 1 2 2 3 3 4 2 5
出力例 1
Alice
例えば、次のようなシナリオが考えられます。
- はじめに Alice が頂点 1 に自分の印をつける。
- Bob が頂点 2 に自分の印をつける(頂点 1 には相手の印がついており、頂点 2 と辺で繋がっている)。
- Alice が頂点 3 に自分の印をつける(頂点 2 には相手の印がついており、頂点 3 と辺で繋がっている)。
- Bob が頂点 4 に自分の印をつける(頂点 3 には相手の印がついており、頂点 4 と辺で繋がっている)。
- Alice が頂点 5 に自分の印をつける(頂点 2 には相手の印がついており、頂点 5 と辺で繋がっている)。
- Bob は操作を行うことができない。Alice の勝ちである。
この木では Alice に必勝法が存在するので、Alice を出力してください。
入力例 2
4 1 2 3 4 3 2
出力例 2
Bob
入力例 3
7 1 2 2 3 3 4 3 5 1 6 6 7
出力例 3
Alice
Score: 100 points
Problem Statement
You are given a tree with N vertices. The vertices of the tree are numbered 1, 2, \dots, N, and the i-th edge (1 \leq i \leq N-1) connects vertex u_i and vertex v_i.
Alice and Bob play a game where they alternately mark vertices with their own markers. Initially, no vertices are marked.
First, Alice chooses any vertex and marks it with her marker. Then, starting with Bob, the two players alternate performing the following operation. The player who cannot make a move loses, and the other player wins.
- Choose a vertex v that satisfies the following conditions:
- Vertex v is not marked.
- There exists a vertex u connected to v by an edge such that u is marked with the opponent's marker.
- Mark the chosen vertex v with their own marker.
Determine the winner when both players adopt the optimal strategy for their own victory.
Constraints
- All input values are integers.
- 1 \leq N \leq 2 \times 10^5
- 1 \leq u_i, v_i \leq N
- The given graph is a tree.
Input
The input is given in the following format:
N
u_1 v_1
\vdots
u_{N-1} v_{N-1}
Output
If Alice wins, output Alice. If Bob wins, output Bob.
Sample Input 1
5 1 2 2 3 3 4 2 5
Sample Output 1
Alice
For example, consider the following scenario:
- Alice starts by marking vertex 1 with her marker.
- Bob marks vertex 2 (vertex 1 is marked by the opponent and is connected to vertex 2 by an edge).
- Alice marks vertex 3 (vertex 2 is marked by the opponent and is connected to vertex 3 by an edge).
- Bob marks vertex 4 (vertex 3 is marked by the opponent and is connected to vertex 4 by an edge).
- Alice marks vertex 5 (vertex 2 is marked by the opponent and is connected to vertex 5 by an edge).
- Bob cannot make a move. Alice wins.
In this tree, Alice has a winning strategy, so you should output Alice.
Sample Input 2
4 1 2 3 4 3 2
Sample Output 2
Bob
Sample Input 3
7 1 2 2 3 3 4 3 5 1 6 6 7
Sample Output 3
Alice
Time Limit: 2 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
Shobon proposed the following problem:
Marunomi
You are given a sequence of positive integers W = (w_1, w_2, \dots, w_N).
There are N living slimes, named Slime 1, 2, \dots, N.
Initially, the weight of Slime i (1 \leq i \leq N) is w_i, and its number of victories is 0.You can perform the following operation on the slimes zero or more times:
- Choose two living slimes, say Slime i and Slime j (i \neq j).
- Let the current weight of Slime i be W_i and that of Slime j be W_j.
- If W_i \gt W_j, the number of victories of Slime i increases by 1, its weight becomes W_i + W_j, and Slime j dies.
- If this condition is not satisfied, nothing happens.
For each i = 1, 2, \dots, N, let S_i be the maximum number of victories Slime i can achieve through your actions.
Calculate the value of S_1 + S_2 + \dots + S_N.
However, since this problem is similar to ARC189 D - Takahashi is Slime, noya2 modified it as follows:
Marunomi for All Prefixes
You are given a sequence of positive integers A = (a_1, a_2, \dots, a_M).
For each i = 1, 2, \dots, M, compute the answer to the Marunomi problem when W = (a_1, a_2, \dots, a_i).
Solve this problem.
Constraints
- All input values are integers.
- 1 \leq M \leq 2 \times 10^5
- 1 \leq a_i \leq 10^9\ (1 \leq i \leq M)
Input
The input is given in the following format:
M a_1 a_2 \cdots a_M
Output
Output M lines. The i-th line (1 \leq i \leq M) should contain the answer to the Marunomi problem for W = (a_1, a_2, \dots, a_i).
Sample Input 1
5 1 2 3 5 20
Sample Output 1
0 1 3 7 11
Sample Input 2
3 1 1 1
Sample Output 2
0 0 0
Sample Input 3
10 17 3467 115 716 9070 32 12251 237 549 17
Sample Output 3
0 1 3 6 10 15 22 29 38 46
配点 : 100 点
問題文
Shobon さんは以下の問題を考えました。
Marunomi
正整数の列 W = (w_1, w_2, \dots, w_N) が与えられます。
N 体の生きているスライムがあり、スライム 1, 2, \dots, N と名付けられています。 最初、スライム i ( 1 \leq i \leq N ) の重さは w_i 、勝利数は 0 です。
これらのスライムに対して、あなたは次の操作を 0 回以上行うことができます。
- 生きているスライムを 2 体選び、それぞれ、スライム i 、スライム j\ (i \neq j) とする。
- 現在のスライム i の重さを W_i 、スライム j の重さを W_j とする。
- W_i \gt W_j を満たすとき、スライム i の勝利数が 1 増加し、重さが W_i + W_j となる。また、スライム j は死亡する。
- そうでないとき、なにも起こらない。
i=1,2,\dots,N のそれぞれについて、あなたがスライム i の勝利数を最大化するように行動した場合のスライム i の勝利数を S_i とします。
S_1 + S_2 + \dots + S_N の値を求めてください。
しかし、この問題は ARC189 D - Takahashi is Slime と似ているため、noya2 さんは以下のように改題しました。
Marunomi for All Prefixes
正整数の列 A = (a_1, a_2, \dots, a_M) が与えられます。
i = 1, 2, \dots, M のそれぞれについて、問題 Marunomi に W = (a_1, a_2, \dots, a_i) を入力したときの答えを求めてください。
この問題を解いてください。
制約
- 入力はすべて整数
- 1 \leq M \leq 2 \times 10^5
- 1 \leq a_i \leq 10^9\ (1 \leq i \leq M)
入力
入力は以下の形式で与えられる。
M a_1 a_2 \cdots a_M
出力
M 行出力せよ。i 行目 (1 ≤ i ≤ M) には、問題 Marunomi に W = (a_1, a_2, \dots, a_i) を入力したときの答えを出力せよ。
入力例 1
5 1 2 3 5 20
出力例 1
0 1 3 7 11
入力例 2
3 1 1 1
出力例 2
0 0 0
入力例 3
10 17 3467 115 716 9070 32 12251 237 549 17
出力例 3
0 1 3 6 10 15 22 29 38 46



