Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 100 点
問題文
天下一大学に入学したキノシタくんは、天下一プログラマーゲームで遊ぶことにしました。 天下一プログラマーゲームとは、整数を 1 から順に数えていき、 その整数が 3 で割り切れる場合には「天下一」、 5 で割り切れる場合には「プログラマー」、 3 でも 5 でも割り切れる場合には「天下一プログラマー」と発言するゲームです。 それ以外の場合には、その整数をそのまま発言します。
キノシタくんは天下一プログラマーゲームを遊んだときにそのまま発言した整数の総和を求めることにしました。
例えば、10 まで天下一プログラマーゲームを遊んだとき、 「1、2、天下一、4、プログラマー、天下一、7、8、天下一、プログラマー」と発言するので、 整数の総和は 1+2+4+7+8=22 となります。
100 まで天下一プログラマーゲームを遊んだときの、そのまま発言した整数の総和を求めてください。
入力
この問題では入力は与えられない。
出力
100 まで天下一プログラマーゲームを遊んだとき、そのまま発言した整数の総和を出力せよ。出力の末尾に改行を入れること。
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 300 点
問題文
ヤマモトくんは、通信環境の悪いネットワークでのアプリケーションの動作検証のために、PackDrop という、0.01 の確率でパケットを破棄する装置を発明しました。
ヤマモトくんは N 台の機器からなるネットワークに、いくつかのPackDropを取り付けて、以下の条件を満たす必要があります。ただし、使用する PackDrop の個数は最少にしたいです。
このネットワークの各機器には 0 から N - 1 の番号がふられています。
機器 0 以外の各機器には 1 台の親機器があり、機器 i の親機器は機器 P_i です。機器 P_i から見た機器 i を子機器といいます。
直接親子関係のある機器は直接つなぐか、PackDrop をいくつか直列にはさんでつなぐことができます。
親機器と子機器が n 個の PackDrop をはさんでつながっているとき、親機器から子機器へのパケットの到達率は 0.99^n となります。すなわち、直接つないだとき、パケットの到達率は 1 となります。
機器 x から 機器 y へのパケットの到達率を p、機器 y から 機器 z へのパケットの到達率を q としたとき、機器 x から 機器 z へのパケットの到達率は p × q となります。
PackDrop がパケットを破棄する以外の要因によりパケットの到達率が変化することはないものとします。
子機器を持たない機器は M 台あり、その番号は B_0, B_1, …, B_{M-1} です。各 i ( 0 \leq i \leq N-1 ) に対して、機器 0 から機器 B_i への到達率を 0.99^{C_i} にしたいとき、最少の PackDrop の個数を求めてください。
制約
- 2 \leq N \leq 1000
- 1 \leq M \leq N - 1
- 0 \leq P_i \leq i - 1
- 1 \leq B_i \leq N - 1
- 1 \leq C_i \leq 100000
- i \neq j ならば B_i \neq B_j である
- P_i = B_j となる i, j は存在しない
- 整数 k ( 1 \leq k \leq N-1 ) が P_1, P_2, …, P_{N-1} に含まれないならば k は B_0, B_1, …, B_{M-1} に含まれる
- N, M, P_i, B_i, C_i は整数である
入力
入力は以下の形式で標準入力から与えられる。
N M
P_1
:
P_{N-1}
B_0 C_0
:
B_{M-1} C_{M-1}
出力
最少の PackDrop の個数を出力せよ。
入力例 1
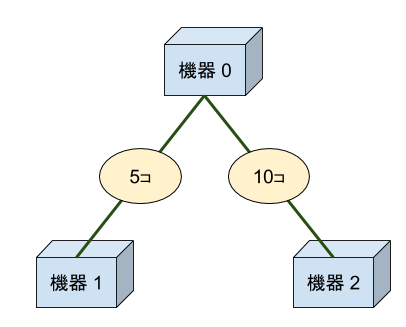
3 2 0 0 1 5 2 10
出力例 1
15
このネットワークに最少の PackDrop をつなぐと下図のようになります。
入力例 2
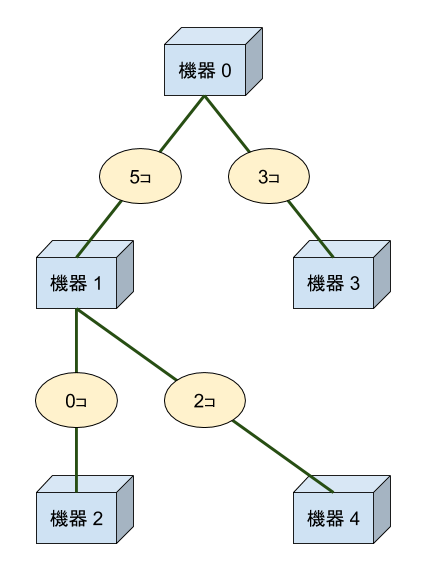
5 3 0 1 0 1 2 5 3 3 4 7
出力例 2
10
このネットワークに最少の PackDrop をつなぐと下図のようになります。
入力例 3
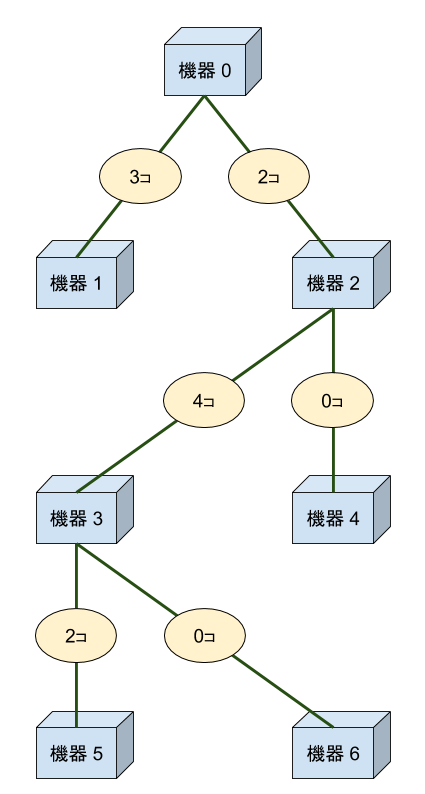
7 4 0 0 2 2 3 3 1 3 4 2 5 8 6 6
出力例 3
11
このネットワークに最少の PackDrop をつなぐと下図のようになります。
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 600 点
問題文
天下一株式会社に勤務するワタナベくんは、社内のコミュニケーションにチャットツールを使っています。 チャットツールには補完機能があり、@で始まるアカウント名を入力しようとすると、プレフィックスの一致するアカウント名の一覧を辞書順で補完候補として表示してくれます。
ところが、ワタナベくんは補完候補の中から @yamamoto を選ぼうとした時に、間違って @yamada を選択してしまうことが多々あります。
@yamada は @yamamoto より辞書順で小さく、 @yama まで入力した際に、候補の先頭に表示されてしまうためです。
ワタナベくんは不思議な特技を持っていて、アルファベットの順番を自由に並べ替えることができます。
例えば、ワタナベくんが特技を使ってアルファベットの順番を abcefghijklmdnopqrstuvwxyz にすると、
m は d より小さくなり、 @yamamoto を @yamada より辞書順で小さくすることができます。
アカウント名 A_i をアカウント名 B_i より辞書順で小さくしたいという要求が N 個与えられます。 与えられた要求をすべて満たすような、ワタナベくんの特技によって並べ替えられたアルファベットの順番を求めてください。 条件を満たすようなアルファベットの順番が複数存在する場合は、並べ替えられる前のアルファベットの順番での辞書順最小の順番を求めてください。
制約
- 1 \leq N \leq 1000
- A_i \neq B_i
- 1 \leq |A_i|, |B_i| \leq 1000
- A_i,B_iは英小文字で構成される
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 : A_N B_N
出力
条件を満たすようなアルファベットの順番のうち、辞書順最小のものを1行に出力せよ。
そのようなアルファベットの順番が存在しない場合は、-1を出力せよ。
入力例 1
1 yamamoto yamada
出力例 1
abcefghijklmdnopqrstuvwxyz
mdabcefghijklnopqrstuvwxyzやmabcefghijklnopqrstuvwxyzdも考えられるが、本来の辞書順で最も小さいabcefghijklmdnopqrstuvwxyzを出力する。
入力例 2
3 xx xy z w v w
出力例 2
abcdefghijklmnopqrstuvxyzw
入力例 3
2 a b b a
出力例 3
-1
条件を満たすようなアルファベットの並びは存在しない。
入力例 4
1 yamamoto yama
出力例 4
-1
yamamotoはyamaより常に大きくなる。
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1100 点
問題文
天下一株式会社では、グラフ理論におけるグラフを視覚的に表現するソフトウェアを開発しています。 特に、あまり複雑でないグラフをテキストベースで見やすく表示するツールが人気です。
N 頂点の無向木が与えられます。 各頂点には、大文字のアルファベットが重複なく割り振られています(頂点の個数は 26 以下です)。
N-1 本の辺のうち i 番目は、頂点 v_i と頂点 w_i を結びます。 ただし、任意の頂点について、その頂点に接続する辺の本数が 4 以下であることが保証されます。
与えられた木を以下のように視覚的に表示するプログラムを作ってください。 詳細は「出力」セクションに記します。
8 12 ............ ...D...E.... ...|...|.... .C-A---B---F .|.....|...| .|.....G.J-I .H.......... ............
制約
- 2≦N≦26
- v_i, w_i は、それぞれ英大文字の最初の N 文字のいずれかである。
- 与えられるグラフは木である。
- 任意の頂点について、その頂点に接続する辺の本数は 4 以下である。
入力
入力は以下の形式で標準入力から与えられる。
N
v_1 w_1
v_2 w_2
:
v_{N-1} w_{N-1}
出力
入力された木を、以下の形式で H+1 行に表示せよ。
H W
c_{1,1}c_{1,2} … c_{1,W}
c_{2,1}c_{2,2} … c_{2,W}
:
c_{H,1}c_{H,2} … c_{H,W}
ここで、
- H, W は以下に続く視覚表示の大きさを表し、半角スペース一つで区切られる。1≦H≦100, 1≦W≦100 を満たさなければならない。
- 視覚表示は、文字を縦 H 文字、横 W 文字の長方形状に並べたものである。
- 視覚表示を構成するそれぞれの文字 c_{i,j} は、英大文字の最初の N 文字および
.、-、|のいずれかであり、以下を満たす。- 木の各頂点は、対応する英大文字で表される。それぞれの頂点は、視覚表示にちょうど一度ずつ現れなければならない。
- 頂点を表す文字は、別の頂点を表す文字と縦または横に隣接してはならない。
- 二つの頂点 a, b が一本の辺で直接結ばれるなら、以下の条件 (A), (B) のうち一方を満たさなければならない。
- (A) 頂点 a, b を表す二つの文字が視覚表示の同じ行にあり、それらに挟まれた文字はすべて
-である。 - (B) 頂点 a, b を表す二つの文字が視覚表示の同じ列にあり、それらに挟まれた文字はすべて
|である。
- (A) 頂点 a, b を表す二つの文字が視覚表示の同じ行にあり、それらに挟まれた文字はすべて
- 二つの頂点 a, b が一本の辺で直接結ばれないなら、上記の条件 (A), (B) を満たすことはどちらも禁止される。
- 以上のように頂点や辺を表す文字以外の文字は、すべて
.でなければならない。
なお、制約を満たす入力に対し、これらの条件を満たす視覚表示が必ず存在することが示せる。そのような視覚表示のうち、どれを出力してもよい。
入力例 1
10 A B A C A D B E B F B G C H F I I J
出力例 1
8 12 ............ ...D...E.... ...|...|.... .C-A---B---F .|.....|...| .|.....G.J-I .H.......... ............
出力例は問題文中で示した例と同一です。
入力例 2
7 A B B C C D D E E F F G
出力例 2
5 4 .A-B E-F| |.|| |.G| D--C
頂点を表す文字が - や | と縦や横に隣接することは禁止されていません。
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1400 点
問題文
天下一研究所は、組合せ数学の研究拠点として様々な活動を行っています。 最近は、無限個の頂点を持つグラフに関する研究が盛んなようです。
正の整数 N と、0 以上 N-1 以下の整数のペア M 組 (A_1, B_1), (A_2, B_2), …, (A_M, B_M) が与えられます。
次のような、無限個の頂点を持つ無向グラフを考えます。
- 任意の整数 z に対し(負の整数も考える)、それに対応する頂点がただ一つ存在する。整数 z に対応する頂点を頂点 z と呼ぶ。どの整数にも対応しない頂点は存在しない。
- 任意の二つの整数 i, k (1 ≦ i ≦ M) に対し、頂点 A_i + k × N と頂点 B_i + (k + 1) × N は一本の辺で直接結ばれる。それらの辺以外に辺は存在しない。
(入力例・出力例のセクションの画像を参考にしてください)
このグラフの連結成分の個数が有限かどうかを判定し、有限ならその個数を求めてください。
制約
- 1 ≦ N ≦ 10^5
- 1 ≦ M ≦ 10^5
- 0 ≦ A_i, B_i ≦ N-1
- すべての組 (A_i, B_i) は異なる。
部分点
- 400 点分のデータセットは以下を満たす。
- 1 ≦ N ≦ 1000
- 1 ≦ M ≦ 1000
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 A_2 B_2 : A_M B_M
出力
与えられたグラフの連結成分の個数が有限なら、その個数を出力せよ。無限なら、代わりに -1 と出力せよ。
入力例 1
2 2 0 0 1 0
出力例 1
1
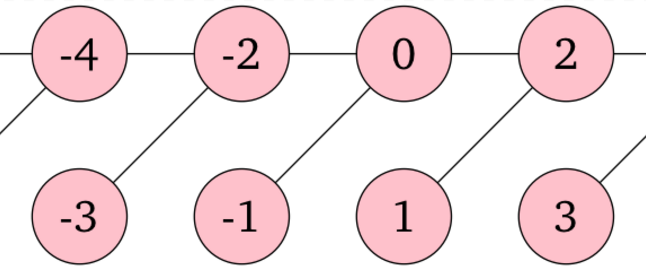
辺をたどって、任意の二頂点間を行き来できます。したがって、このグラフの連結成分の個数は 1 です。
入力例 2
2 2 0 1 1 0
出力例 2
2
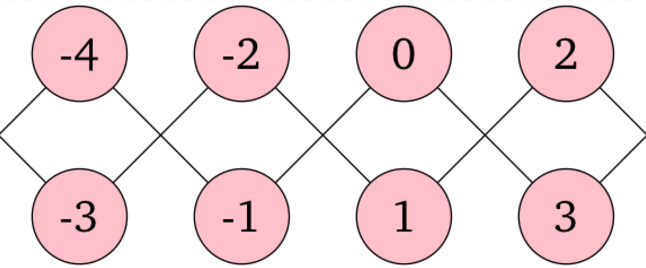
無限の長さを持つ直線状の連結成分が 2 個あります。
入力例 3
3 2 0 1 2 1
出力例 3
-1
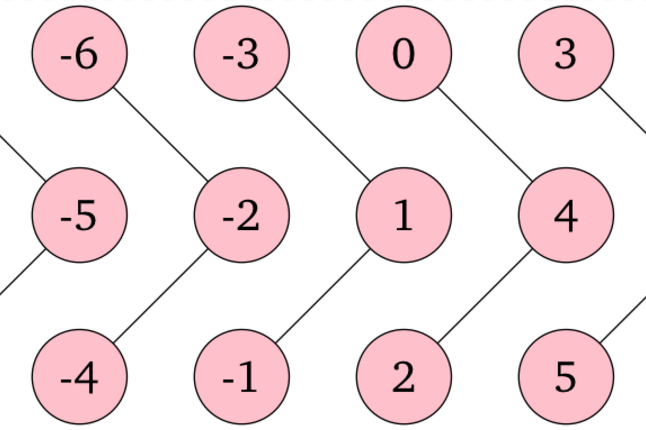
3 頂点からなる連結成分が無限個あります。
入力例 4
7 8 0 3 1 2 1 5 2 5 3 4 4 6 5 2 6 3
出力例 4
4