A - 天下一人力比較

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

天下一株式会社に勤めるカズキ君は、以下の文字列の中から辞書順比較で 7 番目に小さいものを選ぶという仕事を言い渡された。

あなたは唖然とするカズキ君を助けるためにプログラムを書いて、答えを見つけることにした。

  • ABGGEGBCFEBFBAF
  • FFGFACCCECDGCDGAFFFACGDA
  • EEDCAEAFBDDEEDGGA
  • GDCAGFFAACBGEDBAFBCDECGAE
  • EDB
  • GADGADEDBCGABDDCBBDBEAD
  • GADBB
  • DFCE
  • BFGCGCBEDC
  • EDGADBGGDDFEEGGFDGCAFBFGFAAD
  • DDAEBGACDFDGDAB
  • EEDCECFFAE
  • ADDBEEABFEAB
  • FEEBFDGAADAE
  • GB

辞書順比較について

文字列 A に対して、 A_i で i 番目の文字を表し、 |A| で文字列 A の文字数を表すことにすると、文字列 A と文字列 B を辞書順比較で比較するとは、

  • A_i \neq B_i となる最小の i (1 \leq i \leq {\rm min}(|A|,\ |B|)) に対して
    • A_i < B_i であれば、文字列 A は文字列 B より小さい
    • A_i > B_i であれば、文字列 A は文字列 B より大きい
  • そのような i が存在しなければ、文字数が少ない方を小さいとする

として文字列 A と文字列 B の大小関係を決めることである。

なお、アルファベットの大小関係は、 A \lt{} B \lt{} C \lt{} ... \lt{} Y \lt{} Z である。
例えば、 AA, B, BA, AB, A の中から辞書順比較で 3 番目に小さいものは ABである。(A \lt{} AA \lt{} AB \lt{} B \lt{} BA である。)

入力

下記の文字列が標準入力から与えられる。問題文においてカズキ君の渡された文字列と同じである。

ABGGEGBCFEBFBAF
FFGFACCCECDGCDGAFFFACGDA
EEDCAEAFBDDEEDGGA
GDCAGFFAACBGEDBAFBCDECGAE
EDB
GADGADEDBCGABDDCBBDBEAD
GADBB
DFCE
BFGCGCBEDC
EDGADBGGDDFEEGGFDGCAFBFGFAAD
DDAEBGACDFDGDAB
EEDCECFFAE
ADDBEEABFEAB
FEEBFDGAADAE
GB

出力

辞書順比較で 7 番目に小さい文字列を標準出力に 1 行で出力せよ。
なお、行の終端には改行が必要である。

Source Name

天下一プログラマーコンテスト2013 予選B
B - 天下一後入れ先出しデータ構造

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

スタックは最も基本的なデータ構造の1つであり、データを後入れ先出し (Last In First Out) の構造で保持するものである。スタックは最初は空で、要素の追加と取り出しができるが、取り出しは追加されたのが遅い順に行われる。

ある日、天下一株式会社に務めるユウヤ君は、スタックになりきるという仕事を言い渡された。唖然とするユウヤ君を心配するあなたは、以下の形式の入力で与えられる命令の列をユウヤ君の代わりに処理して、後述のような出力を行うプログラムを作成することにした。

入力

入力は以下の形式で標準入力から与えられる。 

Q L
query_1
query_2
...
query_Q
  • 1 行目は、与えられる命令の数 Q (1 \leq Q \leq 10^5) と スタックのサイズ L (1 \leq L \leq 2147483647) が空白区切りで与えられる。
  • 2 行目から Q+1 行目までの Q 行は、i (1 \leq i \leq Q) 番目の 命令が与えられる。

各命令は、以下 4 種類のうちいずれかに該当する。

  1. Push N M
    • スタックに要素 M を N 個追加する。出力は行わない。
  2. Pop N
    • スタックから要素を N 個取り出す。出力は行わない。
  3. Top
    • スタックの先頭要素を 1 行で出力する。この命令でスタックを構成する要素は変更されない。
  4. Size
    • スタックの要素数を 1 行で出力する。

N, M はそれぞれ整数で、 1 \leq N \leq 10^5, -2^{20} \leq M \leq 2^{20} をみたす。

ただし、スタックの先頭要素とは、スタックの要素のうちで最後に追加されたものであり、もしそのときPop 1を行ったとすると取り出される要素である。

部分点

  • Q \leq 50, N \leq 50 の入力に正解すると、60 点満点に対して部分点として、30 点が与えられる。

出力

上記のとおり、与えられた命令を順番に処理していき、Top、またはSizeの入力が与えられた際に出力を行う。

ただし、以下の 3 つの場合、スタックは例外を投げて止まってしまう。

  • Push N M を要素数が L-N より大きいスタックに対して行った場合
  • Pop Nを要素数が N 未満のスタックに対して行った場合
  • Top を空のスタックに対して行った場合

スタックが投げる例外は以下の通りである。

  • Push による例外でプログラムが終了した場合は FULL
  • Pop または Top による例外でプログラムが終了した場合は EMPTY

これらの例外は 1 行で出力され、例外を投げた後のスタックはそれ以降の命令を放棄する。
スタックは最後まで正常に命令を処理できた場合、 SAFE を 1 行で出力して終了する。

入力例 1

7 20
Push 2 3
Push 4 5
Top
Size
Pop 5
Top
Size

出力例 1

5
6
3
1
SAFE

入力例 2

1 10
Push 40 40

出力例 2

FULL

入力例 3

5 10
Push 1 2
Top
Pop 1
Top
Size

出力例 3

2
EMPTY

入力例 4

4 10
Top
Size
Push 1 1
Top

出力例 4

EMPTY

Source Name

天下一プログラマーコンテスト2013 予選B
C - 天下一ジグソーパズルふたたび

Time Limit: 3 sec / Memory Limit: 64 MB

問題文

高橋君のいたずらによりバラバラにされた天下一プログラマーコンテストのポスターを見て触発されたショウヘイ君は、天下一プログラマーコンテストのポスターを下図のようにN \times M のピースに分割したパズルを作ることにした。

上下左右に隣り合うピースの一辺は一方が凸に他方が凹になっており、外周の辺は直線になっている。このとき、一辺が直線で、残り三辺が凹になっているピースを「特殊なピース」とし、これを可能な限り多くなるように配置した時の「特殊なピース」の個数を答えよ。

ただし、四辺が凹のピースは A 個以上、四辺が凸のピースは B 個以下にするという条件が与えられる。

入力

入力は以下の形式で標準入力から与えられる。 

N M A B
  • パズルの縦幅 N、横幅 M ( 2 \leq N, M \leq 8 ) 、四辺が凹のピースの数の下限 A ( A \geq 0 ) 、 四辺が凸のピースの数の上限 B ( B \geq 0 ) が、スペースで区切られて、それぞれ整数で与えられる。
  • A + B \leq (N-2) \times (M-2)
  • 少なくとも 1 通りは条件を満たす分割方法が存在する。

部分点

  • A = 0, B = (N-2) \times (M-2) の入力に正解すると、120 点満点に対して部分点として、30 点が与えられる。
  • M, N \leq 4 の入力に正解すると、120 点満点に対して部分点として 40 点が与えられる。

出力

「特殊なピース」の数の最大値を標準出力に 1 行で出力せよ。
なお、行の終端には改行が必要である。

入力例 1

3 3 0 1

出力例 1

4

下図は4つの「特殊なピース」を持つ、条件を満たした分割方法である。

入力例 2

3 4 1 1

出力例 2

3

下図は3つの「特殊なピース」を持つ、条件を満たした分割方法の一例である。

Source Name

天下一プログラマーコンテスト2013 予選B
D - 天下一二三パズル リベンジ

Time Limit: 8 sec / Memory Limit: 256 MB

問題文

ユウタ君は15パズルと呼ばれるスライドパズルを遊んでいたが簡単すぎて飽きてしまったため、15パズルを大きいサイズに改造してしまった。それでも天下一級のプログラマのユウタ君には簡単すぎたらしく、唖然としてしまった。

改造されたパズルは、12 \times 12 マスの盤面に対して 1 ～ 123までの整数が書かれた 1 \times 1 マスの正方形のピースが 123 個と空白が 21 個配置されている123パズルだった。そして、整数の書かれたピースを、上下左右の空白のマスにスライドさせて、下記の初期配置から完成図にするのが目的である。

この123パズルを解く手順を答えなさい。

初期配置

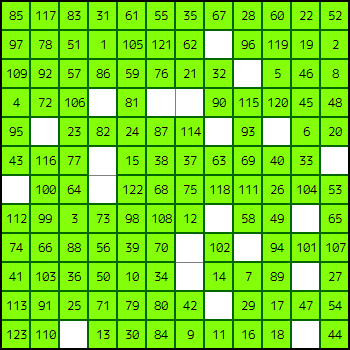
盤面の初期状態は以下の通りである（図 1）。

図 1 初期配置

完成図

盤面の完成図は以下の通りである（図 2）。

図 2 完成図

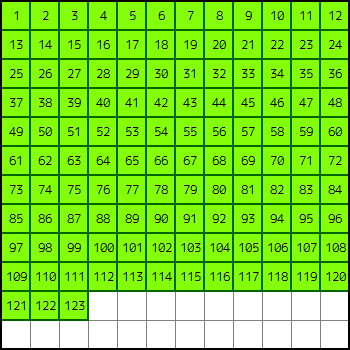
完成図において、i 行目の j 個目のマスは

  • 12 \times (i-1) + j \leq 123なら整数12 \times (i-1) + jが書かれたピースがある
  • 12 \times (i-1) + j > 123なら空白である

となる。

配点

1 つのピースの上下左右への 1 マス分の移動を 1 手として、移動にかかった手数 N によって得点 S を以下の式により決定する。

S = 200 - {\rm floor}(N / 40)
※{\rm floor}(x) でxを超えない最大の整数を意味する。

例えば 1999 手で完成図まで到達した場合、 151 点が与えられる。

ただし、

  • 上記の式が負になる場合
  • 実現できない出力が与えられた場合
  • 完成図に到達しない出力が与えられた場合

は 0 点とする。

入力

初期配置を表す、以下のテキストが標準入力から与えられる。
i 行目に書かれた j 番目の整数は、123パズルにおいて、i 行目の左から j 番目のマスにあるピースに書かれている整数を意味し、0 は空白を表す。 

85 117 83 31 61 55 35 67 28 60 22 52
97 78 51 1 105 121 62 0 96 119 19 2
109 92 57 86 59 76 21 32 0 5 46 8
4 72 106 0 81 0 0 90 115 120 45 48
95 0 23 82 24 87 114 0 93 0 6 20
43 116 77 0 15 38 37 63 69 40 33 0
0 100 64 0 122 68 75 118 111 26 104 53
112 99 3 73 98 108 12 0 58 49 0 65
74 66 88 56 39 70 0 102 0 94 101 107
41 103 36 50 10 34 0 14 7 89 0 27
113 91 25 71 79 80 42 0 29 17 47 54
123 110 0 13 30 84 9 11 16 18 0 44

出力

以下のフォーマットに従って、初期配置から完成図にたどり着くまでの手順を出力すること。 

N
P_1 D_1
P_2 D_2
...
P_N D_N

Nは手数を表し、 P_i, D_i は i手目に動かすピースと動かす方向を意味する。
1 \leq P_i \leq 123で、D_iはup, down, left, right のいずれかでなければならない。
また、出力された手順をN手行ったときに、盤面は完成図になっていなくてはならない。

例えば、 

0 1
2 3
の盤面に 
1 left
3 up
2 right
という手順の移動をさせると 
1 3
0 2
となる。

なお、出力の最後には改行をいれること。
また、あらかじめ計算して出力した結果を、そのまま提出しても良い。その場合は、使用言語にText(cat)を選択して提出すること。

Source Name

天下一プログラマーコンテスト2013 予選B
E - 天下一最短路コンテスト

Time Limit: 8 sec / Memory Limit: 256 MB

問題文

あなたは、天下一最短路コンテストの運営者です。
天下一最短路コンテストでは、以下のようなルールで開催されます。

  • 二次元平面上に N ( 1 ≦ N ≦ 100) 個の点 p_i ( 1 ≦ i ≦ N ) が与えられます
    • 点 p_i のx 座標は x_i で y 座標は y_i です
    • 点の数 N は最大 100 個です
    • 各座標の値 x_i, y_i は全て 10,000 以下の非負の整数です
    • 全ての点の座標は異なります。つまり、i ≠ j のとき、(x_i,\ y_i) ≠ (x_j,\ y_j) を満たします
  • p_1 から始まり、全ての点を通る経路を出力します
  • 経路の長さが最も短い人の勝ちです

高橋君は、天下一最短路コンテストに出場しようとしていますが、ライバルである、KLabのスーパープログラマー、タクヤ君に勝てる気がしません。タクヤ君のプログラムは、オープンソースとして公開されていたので、これを改造することで、コンテストに勝とうと考えました。

タクヤ君のプログラムは、以下のようなプログラムです。

  • 最初に点 p_1 を選び、まだ選んでいない点が存在する間、以下の手順で点を選ぶ
    • 最後に選んだ点から、最も近い、まだ選んでいない点を選ぶ
    • 最も近い点が複数ある場合は、その中でidが一番小さいものを選ぶ（点 p_i のidは i ）
  • 点を選ばれた順番に、線分で結んで、それを経路として出力する

このプログラムを、高橋君が改造した結果、以下のようになりました。

  • 最初に点 p_1 を選び、まだ選んでいない点が存在する間、以下の手順で点を選ぶ
    • まだ選んでいない点が 3 つ以上ある場合、最後に選んだ点から 2 番目に近い点を選ぶ
      • この際、最も近い点が、最後に選んだ点と 2 番目に近い点とを結ぶ線分の上にあったとしても、最も近い点は選ばれたとみなされない
    • まだ選んでいない点が 2 つ以下の場合、最後に選んだ点から最も近い点を選ぶ
      • 最も近い点が選ばれるのは、最後の 1 回ではなく、 2 回であることに注意してください
    • 同じ距離の点が複数ある場合は、idの小さいものほど近い点であるとみなす
  • 点を選ばれた順番に、線分で結んで、それを経路として出力する

この 2 つのプログラムを戦わせてみたところ、殆どの場合で、高橋君が負けてしまいます。ですが、このままだと高橋君が可哀想なので、高橋君が引き分け以上の結果を残せる入力を１つだけ用意することにしました。
あなたは、高橋君が引き分け以上の結果を出す、可能な限り頂点数の多いデータセットを作らなければいけません。

入力

入力は与えられない。

出力

高橋君が引き分け以上の結果を出すことができるデータセットを出力しなさい。出力は以下の形式で行う。
N
x_1 y_1
x_2 y_2
:
x_N y_N

  1. 1行目には、データセットの頂点数 N (1≦N≦100) を 1 行で出力する
  2. 2行目には、各点の x 座標 x_i、y 座標 y_iを、x_i y_iの順でスペース区切りに、N行で出力する ( 0 ≦ x_i, y_i ≦ 10,000)
  3. 条件を満たすデータセットであれば、N×2点の点数が得られます。
二つのプログラムの出力する経路の長さの、絶対的な差または相対的な差が 10^{-9}以下であれば、二つのプログラムは引き分けとみなす。
つまり、二つのプログラムの出力する経路の長さがそれぞれd_1, d_2であるとき、\frac{|d_1 - d_2|}{{\rm max}(1, d_1, d_2)} ≦ 10^{-9}であれば、引き分けとみなす。
また、出力の最後には改行をいれること。
なお、あらかじめ計算して出力した結果を、そのまま提出しても良い。その場合は、使用言語にText(cat)を選択して提出すること。

出力例 1

1
1 1
  • 点が 1 個の時、どちらのプログラムも出力する経路の長さは 0 となり、引き分けとなります
  • この出力を提出すると、 2 点を得ることが出来ます

出力例 2

5
4 6
2 5
6 10
1 2
1 6
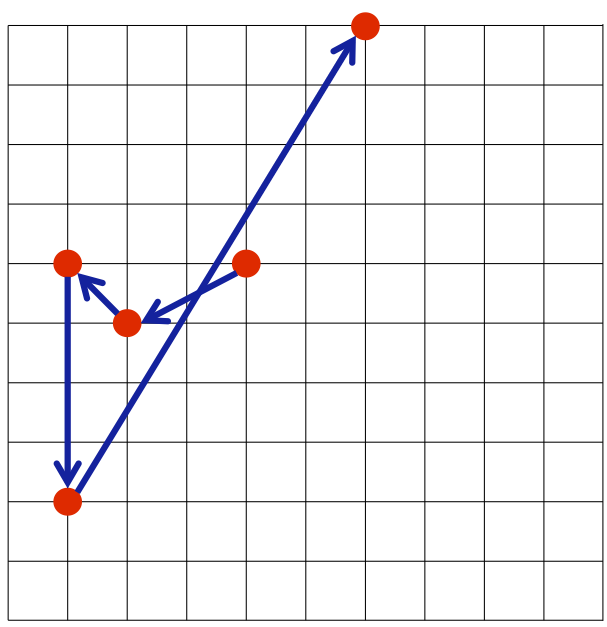
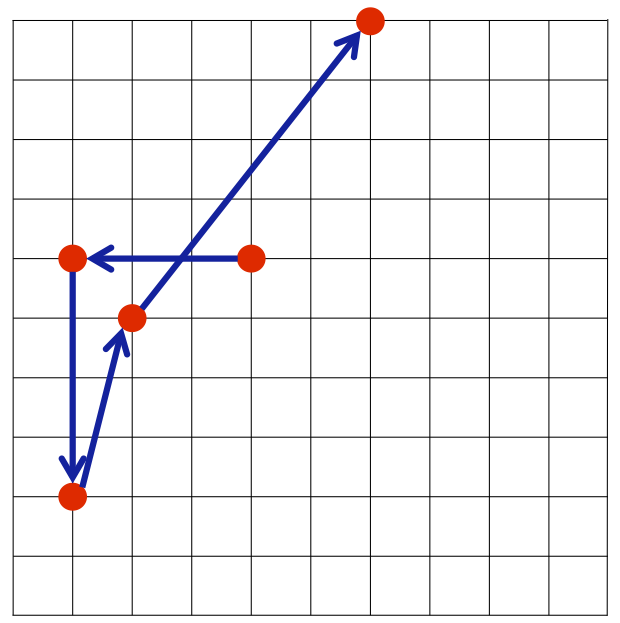
  • タクヤ君のプログラムが求める経路は、 (4,6) → (2,5) → (1,6) → (1,2) → (6,10)であり、この経路の長さは約17.084です
    • 図 1タクヤ君のプログラムの経路
  • 高橋君のプログラムが求める経路は、 (4,6) → (1,6) → (1,2) → (2,5) → (6,10)であり、この経路の長さは約16.565です
    • 図 2高橋君のプログラムの経路
  • この出力を提出すると、 10 点を得ることができます