A - ぶんたん

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

フィボナッチ数列は、以下のような漸化式で表される数列 F_0,\ F_1,\ F_2,\ …\ (=0,\ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ …) であり、フィボナッチ数はこの数列に現れる数 F_i\ (i \geq 0) です。

  • F_{0} = 0
  • F_{1} = 1
  • F_{i+2} = F_{i} + F_{i+1} (i \geq 0)

ある正整数 n をいくつかのフィボナッチ数の和として表すことを考えます。
このとき、和が正整数 n となるフィボナッチ数の個数として考えられる最小の値を答えなさい。
ただし、同じフィボナッチ数を複数回用いることもできるものとし、複数回用いた場合はそれぞれ別々に数えるものとします。

入力

入力は以下の形式で標準入力から与えられる。 
n
  • 正整数 n (1 \leq n \leq 10^{10}) が 1 行で与えられる。

部分点

与えられる数が小さい入力 (1 \leq N \leq 10^5) のみ正解すると、100 点満点に対して部分点として 50 点が与えられる。

出力

和が正整数 n となるフィボナッチ数の個数として考えられる最小の値を 1 行で出力せよ。
なお、行の終端には改行が必要である。

入力例 1

10

出力例 1

2
    10 は最小で 5 ,\ 5 の 2 個のフィボナッチ数の和で表すことができます。

入力例 2

11

出力例 2

2
    11 は最小で 3 ,\ 8 の 2 個のフィボナッチ数の和で表すことができます。

入力例 3

10000000000

出力例 3

16
B - よんてん

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

x 座標と y 座標がともに整数である平面上の点が N 個与えられます。

これらの点から、いずれの 3 点も一直線上に並ばない 4 点の選び方が何通りあるのかを、1,000,000,007 で割った余りで答えなさい。

入力

入力は以下の形式で標準入力から与えられる。 
N
x_1 y_1
:
x_N y_N
  • 1 行目には、与えられる点の数を表す N が与えられる。
  • 2 行目からの N 行には、i 番目の点の x 座標 x_i と y 座標 y_i が空白区切りで与えられる。
  • 4 \leq N \leq 10^4
  • 0 \leq x_i \leq 99\ (1 \leq i \leq N)
  • 0 \leq y_i \leq 99\ (1 \leq i \leq N)
  • i \neq j ならば、 x_i \neq x_j または y_i \neq y_j

部分点

与えられる点が 4 点の入力（N = 4）に正解すると、100 点満点に対して部分点として 4 点が与えられる。
与えられる点の数が 100 以下の入力（N \leq 100）に正解すると、100 点満点に対して部分点として、さらに 16 点が与えられる。
与えられる点の数が 1000 以下の入力（N \leq 1000）に正解すると、100 点満点に対して部分点として、さらに 30 点が与えられる。

出力

いずれの 3 点も一直線上に並ばない 4 点の選び方の数を 1,000,000,007 で割った余りを 1 行で出力せよ。
なお、行の終端には改行が必要である。

入力例 1

4
0 0
0 1
1 0
1 1

出力例 1

1

入力例 2

5
0 0
0 1
0 2
2 0
2 2

出力例 2

3
  • \{(0,0),\ (0,1),\ (2,0),\ (2.2)\}, \{(0,0),\ (0,2),\ (2,0),\ (2.2)\}, \{(0,1),\ (0,2),\ (2,0),\ (2.2)\} の 3 通りである。
C - Code Art Online

Time Limit: 2 sec / Memory Limit: 256 MB

問題文

Code Art Online は符号《コード》の世界のRPGです。 プレーヤーは符号《コード》を生成して戦います。 符号《コード》は文字《グラム》を連ねることで生成します。

このゲームには、あなたの操作する プレーヤー と、プレーヤーに立ちはだかる 敵 という2種類のキャラクターが登場します。
1 ターンは、敵の攻撃、プレーヤーの攻撃、敵の回復、プレーヤーの回復の順に行われます。

ゲーム開始時のプレーヤーの HP（体力）は 100 であり、これが 0 以下になるとゲームオーバーです。
あなたは、プレーヤーを以下の3種類の文字《グラム》を使って操作することができます。

  • A : 敵の HP に 5 ダメージを与える
  • B : B が連続した数だけ敵の HP にダメージを与える
  • C : プレーヤーの HP を 50 回復する
例えば、BBB と操作すると、1 ターン目に 1 ダメージ、2 ターン目に 2 ダメージ、3 ターン目に 3 ダメージを敵の HP に与えます。
プレーヤーの最大 HP は 100 であり、これを超えて回復しようとした場合には HP は 100 となります。
同一ターン内の被ダメージ処理と回復処理は被ダメージ処理の方が先に行われるので、被ダメージ処理が終わった段階で HP が 0 以下になった場合、その時点でゲームオーバーとなります。

敵には最大 HP と攻撃力と回復力のパラメーターがあります。
敵の HP は現れた時には最大 HP と同じ値です。
毎ターンに攻撃力の値だけプレーヤーの HP にダメージを与え、回復力の値だけ HP を回復します。
ただし、最大 HP を超えて回復しようとした場合は、HP は最大 HP と同じ値になります。
敵の回復処理はプレーヤーと同じく被ダメージ処理の後に行われるので、被ダメージ処理が終わった段階で HP が 0 以下になった場合、回復は行われずその敵は倒れます。
敵が複数存在する場合、戦っている敵を倒すと自動的に次の敵が現れ、次のターンにはその敵と戦うことになります。

例えば、敵が 2 体いて、1 体目の敵の HP が 10、攻撃力が 15、回復力が 1 であり、2 体目の敵の HP が 20、攻撃力が 10、回復力が 2 であるとします。
この時、AAACBBBBBB という符号《コード》で戦えば、次のように 2 体の敵を倒すことができます。 

ターン 符号 プレーヤーHP 敵HP
    1   A         85    6
    2   A         70    2
    3   A         55    0  # 一体目の敵を撃破
    4   C         95   20  # プレーヤーは10ダメージを受けた後に50回復する
    5   B         85   20  # 敵は1ダメージ受けた後に1回復する
    6   B         75   20  # 敵は2ダメージ受けた後に2回復する
    7   B         65   19
    8   B         55   17
    9   B         45   14
   10   B         35   10
   11   B         25    5
   12   B         15    0

敵の数とそれぞれの敵の HP、攻撃力、回復力を与えるので、すべての敵をゲームオーバーせずに最短ターン数で倒す符号《コード》の長さを答えなさい。

入力

入力は以下の形式で標準入力から与えられる。 
N
a_1 b_1 c_1
:
a_N b_N c_N
  • 1 行目には敵の数 N (1 \leq N \leq 30) が与えられます。
  • 2 行目から N+1 行目までには、それぞれの敵の HP a_i (1 \leq a_i \leq 100)、攻撃力 b_i (0 \leq b_i \leq 100)、回復力 c_i (0 \leq c_i \leq 100) がスペース区切りで与えられます。

出力

ゲームオーバーせずに最短ターン数で倒す符号《コード》の長さを出力せよ。
敵を倒すことが不可能であれば、 -1 を出力せよ。
なお、行の終端には改行が必要である。

入力例 1

2
10 15 1
20 10 2

出力例 1

10

入力例 2

5
63 15 11
15 5 3
67 17 11
21 4 5
43 8 10

出力例 2

-1

入力例 3

9
64 1 0
89 3 3
91 4 0
99 0 3
32 2 0
10 3 1
82 1 3
1 1 2
8 5 0

出力例 3

37
D - さんかく

Time Limit: 2 sec / Memory Limit: 256 MB

問題文

平面上に存在する N（N は 3 の倍数）個の点を用いて三角形を N/3 個作り、その面積の合計値を出来るだけ大きくするゲームがあります。
ただし、i（0≦i≦N-1）番目の点を示す X 座標の値 x_i と Y 座標の値 y_i はそれぞれ 0≦x_i≦100,000 と 0≦y_i≦100,000 を満たします。

高橋君はこのゲームをコンピュータを使って挑戦します。
しかし、彼は良いアルゴリズムが思いつかなかったため、ランダムで解くことにしました。

高橋君はランダムに 3 つずつ点を選び、N/3 個の三角形を作ります。
これを 1,000 万回行い、最も良かった答えを採用します。

貴方は、高橋君の解答と同じか、それよりより値が大きくなる解答を作りたいです。
そのような三角形の組み合わせを出力してください。

入力

入力は以下の形式で標準入力から与えられる。 
N
x_0 y_0
:
:
x_{N-1} y_{N-1}
  • 入力は N+1 行ある。
  • 1 行目には平面上の点の個数を表す整数 N\ (3≦N≦3,000) が与えられる。ただし、N は 3 の倍数である。
  • 2 行目から N+1 行目までの N 行は点の座標を示している。
    • i\ (0≦i≦N-1) 番目に与えられる座標 (x_i, y_i) は 0≦x_i≦100,000 かつ 0≦y_i≦100,000 の範囲でランダムに与えられる。
    • 0≦i≦N-1 と 0≦j≦N-1 を満たし、i≠j である 2 つの整数 i と j において、x_i≠x_j もしくは y_i≠y_j の少なくとも片方を満たすことが保証されている。

部分点

テストデータには以下に示す 4 種類のデータセットのいずれかが含まれており、それぞれ与えられる点の数である N の値が異なっている。
あるデータセットに対して、高橋君が選択した三角形の面積の合計値と等しい、もしくは大きい解答を出力できたとき、あなたはそのデータセットに対して 2 点を得ることができる。
  • level1 (各 2 点、10 個): N=9
  • level2 (各 2 点、10 個): N=18
  • level3 (各 2 点、15 個): N=300
  • level4 (各 2 点、15 個): N=3,000

出力

三角形の面積の合計値が高橋君の解答と同じか、もしくはそれより大きい解答となる三角形の組み合わせを、頂点となる番号で出力せよ。
各三角形の頂点となる番号を 1 行につき 1 つの三角形が構成されるように出力し、半角スペースで区切ること。
また各三角形を出力する順番、および 1 つの三角形における頂点の出力の順番は問わない。
なお、行の終端には改行が必要である。

入力例 1

9
0 0
1 0
2 0
0 1
1 1
2 1
0 2
1 2
2 2

出力例 1

3 7 2
4 8 1
6 0 5
  • 入力例 1 を図示すると、上図のようになります。
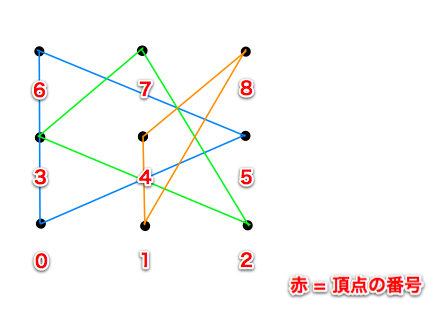
  • 入力例 1 に対して、高橋君のアルゴリズムでは、上図のように点を選択します。この例と同じ面積、もしくは面積の合計が大きい回答を出力してください。

入力例 2

18
0 0
1 0
2 0
0 1
1 1
2 1
0 2
1 2
2 2
0 3
1 3
2 3
0 4
1 4
2 4
0 5
1 5
2 5

出力例 2

11 0 15
3 7 10
6 16 5
2 17 9
12 14 1
8 13 4
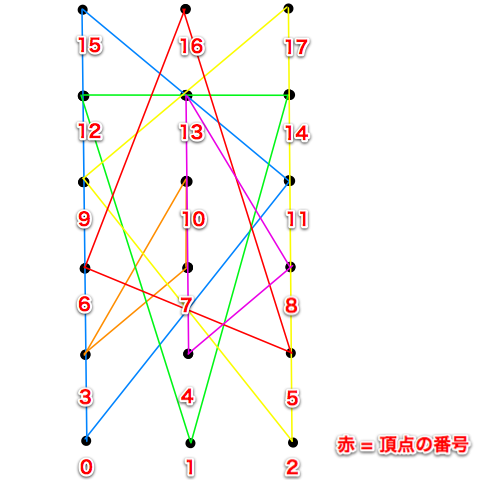
  • 入力例 2 に対して、高橋君のアルゴリズムでは、上図のように点を選択します。この例と同じ面積、もしくは面積の合計が大きい回答を出力してください。
E - GO!GO! サイコロ線路

Time Limit: 2 sec / Memory Limit: 256 MB

問題文

N × N 個のサイコロが XY 平面上に下図のように配置されています。
隣接している面の数字が同じサイコロに移動することができ、貴方は左上のサイコロから右下のサイコロへ移動したいです。
サイコロを 90° 回転させることができる回数が与えられたとき、経由しなければならないサイコロの最小数を出力しなさい。
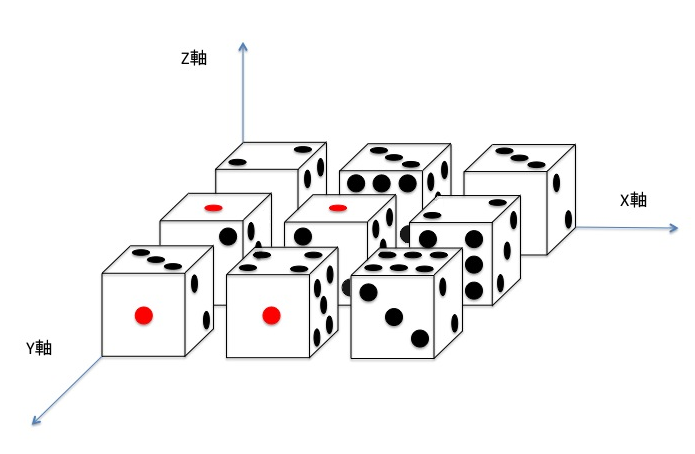
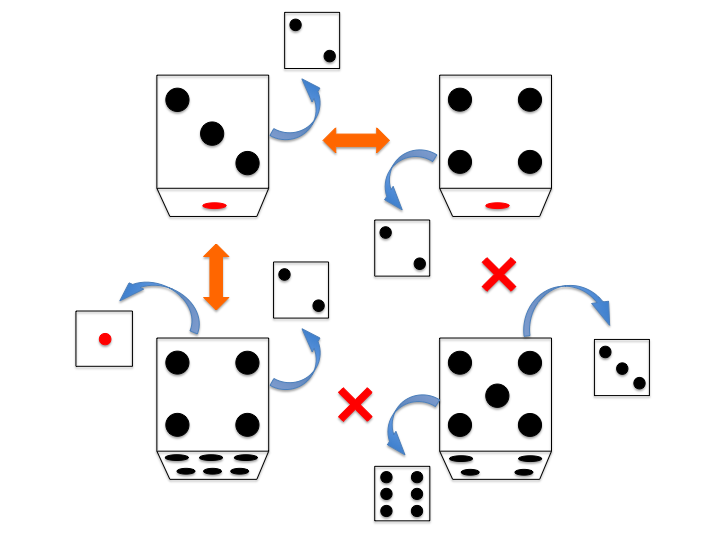
また、左上から右下へ移動できないときは -1 を出力しなさい。
なお、一度移動し始めたら、それ以降サイコロを回転することは出来ません。

入力

入力は以下の形式で標準入力から与えられる。 
N M
c_{00Z}c_{00X} c_{01Z}c_{01X} c_{02Z}c_{02X} … c_{0(N-1)Z}c_{0(N-1)X}
c_{10Z}c_{10X} c_{11Z}c_{11X} c_{12Z}c_{12X} … c_{1(N-1)Z}c_{1(N-1)X}
:
:
c_{(N-1)0Z}c_{(N-1)0X} c_{(N-1)1Z}c_{(N-1)1X} c_{(N-1)2Z}c_{(N-1)2X} … c_{(N-1)(N-1)Z}c_{(N-1)(N-1)X}
  • 入力は N+1 行ある。
  • 1 行目にはサイコロを敷き詰めたときの縦と横の長さ N\ (1≦N≦6) と、サイコロを回転させることのできる回数 M\ (0≦M≦1,000) が与えられる。
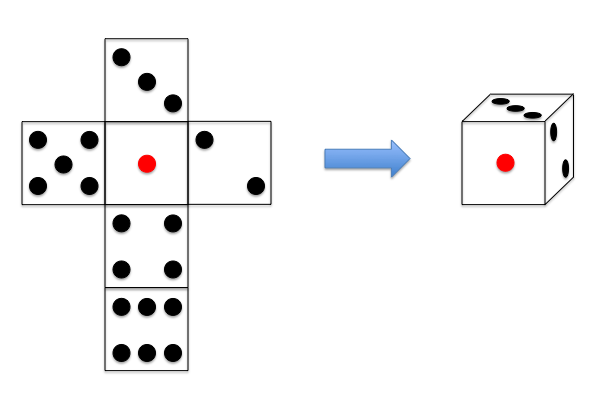
  • 2 行目から N+1 行目までの N 行はサイコロの情報を示し、1 から 6 までの整数 2 桁ごとに半角スペースで区切られている。
  • サイコロの情報は 2 つの整数 i\ (0≦i≦N-1)、j\ (0≦j≦N-1)を用いて以下のように示されている。
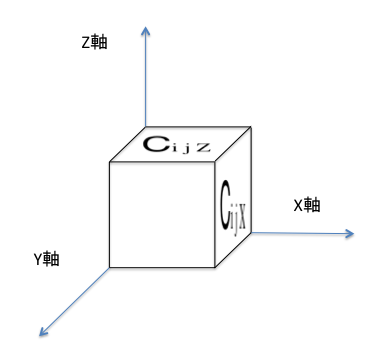
    1. c_{ijZ} … Z 軸正方向に面し、座標 (x_i,y_j) にあるサイコロの値
    2. c_{ijX} … X 軸正方向に面し、座標 (x_i,y_j) にあるサイコロの値
  • M はサイコロを回転させることができる回数で、サイコロの回転は以下のように定義されている。
    1. Z に対して 90° 回転することを 1 回とカウントする。
    2. X に対して 90° 回転することを 1 回とカウントする。
    3. Y に対して 90° 回転することを 1 回とカウントする。
    4. つまり、サイコロの回転軸は 3 つ存在する。

部分点

テストデータには以下に示す 4 種類のデータセットのいずれかが含まれており、それぞれサイコロを敷き詰めたときの縦と横の長さを表す N の範囲が異なっている。
あるデータセットに対して全て正しい解を出力すると、それ以外のデータセットで不正解を出力しても以下のように部分点が与えられる。
  • level1 (25 点) : N≦3
  • level2 (25 点) : N≦4
  • level3 (25 点) : N≦5
  • level4 (25 点) : N≦6

出力

サイコロ c_{00} からサイコロ c_{(N-1)(N-1)} へ移動するときに経由しなければならないサイコロの最小値。
サイコロ c_{00} からサイコロ c_{(N-1)(N-1)} へ到達不能な場合は、-1 を出力せよ。
なお、出力の終端には改行が必要である。

補足

この問題で使用するサイコロの展開図と、それを組み立てたものを以下に示す。

入力例 1

3 1
24 35 32
13 15 23
32 45 62

出力例 1

5
  • 入力例 1 を図示すると、上図のようになります。
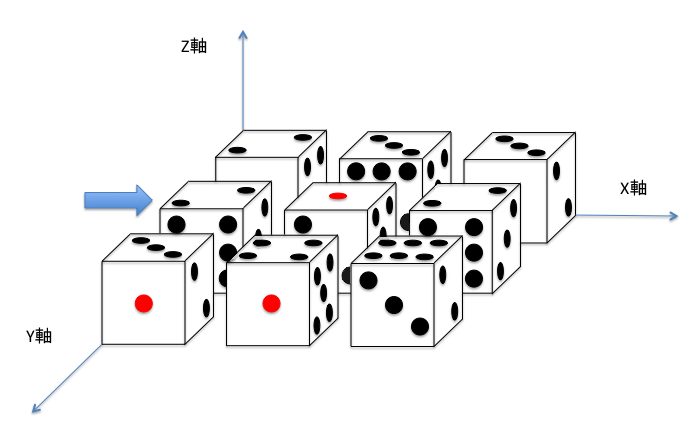
  • 座標 (0,1) のサイコロ（矢印で指しているサイコロ）を Y 軸負の方向に 90° 回転させると、上図のようになります。
  • このとき、左上のサイコロ c_{00} から右下のサイコロ c_{22} へ 5 つのサイコロを通過することで到達できます。

入力例 2

4 2
51 63 26 51
64 21 13 14
51 56 35 62
41 14 21 31

出力例 2

-1

入力例 3

4 3
51 63 26 51
64 21 13 14
51 56 35 62
41 14 21 31

出力例 3

9