問題文

正整数 N と (1,2,\dots ,N) の順列 P=(P_1,P_2,\dots ,P_N) が与えられます。

整数組 (L,R) に対して、f(L,R) を次のように再帰的に定めます。

• 1\le L\lt R\le N のとき、整数 a, b を P_L,P_{L+1},\dots, P_{R} のうち最も小さいものとその次に小さいものがそれぞれ P_a,P_b となるように定義する。f(L, R) = f(\min(a, b) + 1, \max(a, b) - 1) + 1 と定める。
• そうでないとき、f(L,R)=0 と定める。

k=1,2,\dots, N のそれぞれについて、整数組 (L,R) であって f(L,R)=k を満たすものの個数を求めてください。

制約

• 入力はすべて整数
• 2\le N\le 3\times 10^5
• (P_1,P_2,\dots, P_N) は (1,2,\dots, N) の順列

入力例 1

7
2 6 5 1 4 7 3

出力例 1

14
7
0
0
0
0
0

f(1,7) は次のように定められます。P_1,P_2,\dots, P_7 のうち最も小さいものとその次に小さいものはそれぞれ P_4,P_1 です。したがって f(1,7)=f(2,3)+1 です。

f(2,3) は次のように定められます。P_2,P_3 のうち最も小さいものとその次に小さいものはそれぞれ P_3,P_2 です。したがって f(2,3)=f(3,2)+1 です。

f(3,2)=0 なので f(2,3)=1 です。したがって f(1,7)=2 です。

入力例 2

5
1 2 3 4 5

出力例 2

10
0
0
0
0

入力例 3

9
8 6 2 4 9 7 3 5 1

出力例 3

25
8
3
0
0
0
0
0
0

問題文

(1, 2, \dots, N) の順列 P = (P_1, P_2, \dots, P_N) が与えられます。

長さ N - 1 の正整数列 T = (T_1, T_2, \dots, T_{N - 1}) に対して、f(T) を以下の問題で出力される値と定義します。

あなたは P に対する操作を好きな回数 (0 回でもよい) 行うことができます。t 番目の操作では、以下の操作を行います。

• T_i \le t を満たす i を昇順に並べた列を I とする。j = 1, 2, \dots, |I| の順に、P_{I_j} と P_{I_j + 1} をスワップする。（ P_{I_j + 1} は P_{I_{j + 1}} ではないことに注意すること。）

P を昇順にソートするのに必要な操作回数の最小値を出力してください。ただし、ソートできないならば {10}^{100} を出力してください。

すべての正整数列 T に対する f(T) の最小値を求めてください。なお、この問題の制約下で、f(T) < {10}^{100} を満たす T が必ず存在することが証明できます。

制約

• 入力はすべて整数
• 2 \le N \le 5000
• 1 \le P_i \le N
• P_i \ne P_j (i \ne j)

部分点

• 追加の制約 N \le 400 を満たすデータセットに正解した場合は 30 点が与えられる。

入力例 1

4
4 2 1 3

出力例 1

2

T=(2,1,2) とすると、1 番目の操作で P=(4,1,2,3) となり、2 番目の操作で P=(1,2,3,4) となるため、f(T) = 2 が成り立ちます。f(T) < 2 を満たす T は存在しないため答えは 2 となります。

入力例 2

20
15 13 7 3 4 8 16 12 2 5 1 17 11 18 9 19 20 10 6 14

出力例 2

39

問題文

整数 N, X, Y, K, M が与えられます。長さ N の整数列からなる 3 つ組 (A, B, C) であって、以下の条件をすべて満たす組の個数を M で割ったあまりを求めてください。ただし、数列 a の k 番目の要素を a_k と表すこととします。

• i = 1, 2, \dots, N について、(A_i, B_i, C_i) は (1, 2, 3) の順列である。
• A に含まれる 1, 2 の個数はそれぞれ X, Y である。
• A の転倒数と B の転倒数と C の転倒数の合計は K である。

制約

• 入力はすべて整数
• 2 \le N \le 50
• 0 \le X, Y \le N
• X + Y \le N
• 0 \le K \le \frac{3}{2}N(N - 1)
• {10}^8 \le M \le {10}^9

入力例 1

3 1 1 4 998244353

出力例 1

24

条件を満たす (A, B, C) は 24 通り存在します。例えば、A = (1, 2, 3), B = (3, 3, 2), C = (2, 1, 1) とすると、(A, B, C) は条件を満たします。

入力例 2

4 0 0 18 123456789

出力例 2

0

条件を満たす (A, B, C) は存在しません。

入力例 3

50 10 20 1000 1000000000

出力例 3

805988728

問題文

正整数 N, M が与えられます。

k = 1, 2, \dots, N + M - 1 に対して、以下の問題の答えを \mathrm{ans}_{k} とします。

長さ N + M - 1 の数列 a = (a_{1}, a_{2}, \dots , a_{N + M - 1}), b = (b_{1}, b_{2}, \dots, b_{N + M - 1}) の組 (a, b) であって、以下の条件をすべて満たすものを良い数列の組とします。

• (a_1,b_1)=(1, N+1)
• i=2,3,\dots, N+M-1 について、次のいずれかが成り立つ
  • (a_i, b_i) = (a_{i - 1} + 1, b_{i - 1})
  • (a_i, b_i) = (a_{i - 1}, b_{i - 1} + 1)
• (a_{N+M-1}, b_{N+M-1})=(N, N+M)

良い数列の組 (a, b) に対して、木 T(a, b) を以下の条件をすべて満たすものとして定めます。

• 頂点に 1 から N + M までの番号がついた N + M 頂点の木
• i = 1, 2, \dots, N + M - 1 について、頂点 a_{i} と頂点 b_{i} を結ぶ辺が存在する

木に対して頂点 i と頂点 j を結ぶ単純パスに含まれる辺の個数を \mathrm{dist}(i,j) とし、木のスコアを 1\leq i < j\leq N + M かつ \mathrm{dist}(i, j) = k を満たす整数の組 (i, j) の個数とします。

すべての良い数列の組 (a, b) に対する T(a, b) のスコアの総和を 998244353 で割ったあまりを求めてください。

\mathrm{ans}_1, \mathrm{ans}_2, \dots, \mathrm{ans}_{N+M-1} をすべて求め、\displaystyle \sum_{k = 1}^{N + M - 1} (\mathrm{ans}_{k}\oplus k) を出力してください。ここで、\oplus はビットごとの排他的論理和です。

制約

• 入力はすべて整数
• 1\leq N\leq 5\times 10^{6}
• 1\leq M\leq 5\times 10^{6}

入力例 1

2 2

出力例 1

14

(\mathrm{ans}_1,\mathrm{ans}_2,\mathrm{ans}_3) = (6, 4, 2) となるため、出力すべき値は、(6\oplus 1) + (4\oplus 2) + (2\oplus 3) = 7 + 6 + 1 = 14 です。

入力例 2

24 167

出力例 2

21925979855

入力例 3

4297614 4167924

出力例 3

4162418864110099

問題文

長さ N の正整数列 A=(A_1,A_2,\dots, A_N) が与えられます。

Q 個のクエリに答えてください。i 個目のクエリでは整数 L_i,R_i が与えられるので、次の問題に B = (A_{L_i},A_{L_i+1},\dots ,A_{R_i}) を与えたときの答えを求めてください。

正整数列 B=(B_1,B_2,\dots, B_{|B|}) が与えられます。正整数列 C=(C_1,C_2,\dots, C_k) が B の非空な部分列として 2 回以上現れるとき、形式的には、正整数 k と 2 つの添字の列 (i_1,i_2,\dots ,i_k),(j_1,j_2,\dots ,j_k) が存在して以下の条件をすべて満たすとき、 C を良い列とします。

• 1\le i_1\lt i_2\lt \dots \lt i_k\le |B|
• 1\le j_1\lt j_2\lt \dots \lt j_k\le |B|
• p=1,2,\dots ,k に対して B_{i_p}=B_{j_p}=C_p が成り立つ。
• ある p\ (1\le p\le k) が存在して i_p\neq j_p が成り立つ。

良い列が存在するかどうか判定し、存在する場合は良い列のうち辞書順で最大のものの ローリングハッシュ を答えてください。ただし、正整数列 a=(a_1,\dots, a_n) の ローリングハッシュ は \displaystyle \left(\sum_{i=1}^{n}a_i 3^{i-1}\right)\bmod 998244353 と定義します。存在しない場合は -1 を答えてください。

制約

• 入力はすべて整数
• 1\le N,Q\le 3\times 10^5
• 1\le A_i\le N\ (1\le i\le N)
• 1\le L_i\le R_i\le N\ (1\le i\le Q)

入力例 1

5 4
3 2 1 2 3
1 5
1 3
2 4
2 5

出力例 1

36
-1
2
11

1 個目のクエリについて説明します。 B=(3,2,1,2,3) の非空な部分列として 2 回以上現れるもののうち辞書順で最大のものは (3,2,3) です。これを与える 2 つの添字の列としては (1,2,5),(1,4,5) を取ることができます。

2 個目のクエリでは B=(3,2,1) で、非空な部分列として 2 回以上現れるものは存在しません。

3 個目のクエリでは B=(2,1,2) で、非空な部分列として 2 回以上現れるもののうち辞書順で最大のものは (2) です。

4 個目のクエリでは B=(2,1,2,3) で、非空な部分列として 2 回以上現れるもののうち辞書順で最大のものは (2,3) です。

入力例 2

5 1
3 2 1 4 1
1 5

出力例 2

18

入力例 3

10 10
1 4 5 2 5 3 4 2 5 4
1 10
1 9
2 10
1 8
2 9
3 10
1 7
2 8
3 9
4 10

出力例 3

56
20
56
35
20
56
17
35
20
17

問題文

1, 2, …, 9 の数字からなる長さ N の文字列 S が与えられます。

全部で \frac{N(N+1)}{2} 個のブロックからなる三角形のピラミッドがあります。

ピラミッドは N 個の層に分かれており、上から順に層 1, 2, \dots, N と番号付けられています。さらに、層 i (1 \le i \le N) には i 個のブロックが左右一列に並んでいます。各ブロックには文字列が書かれており、層 i の左から j 番目のブロック (1 \le j \le i) に書かれている文字列を C_{i,j} と表します。

C_{i,j} について、以下のことが成り立ちます。

• i = N ならば、C_{i, j} は S の j 番目の文字のみからなる長さ 1 の文字列である。
• 1 \le i < N ならば、C_{i, j} は C_{i+1,j} と C_{i+1,j+1} をこの順に結合したものである。

C_{1,1} を十進表記の整数として見たときの値を 998244353 で割ったあまりを求めてください。

制約

• N は整数
• 1 \le N \le 2 \times 10^5
• S は 1, 2, …, 9 からなる長さ N の文字列

入力例 1

4
8192

出力例 1

81191992

S = 8192 です。ピラミッドは下図の通りになり、C_{1,1} = 81191992 です。

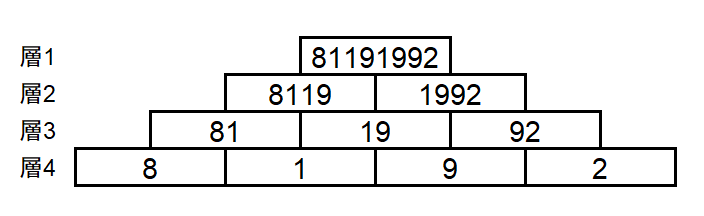
入力例 2

1
5

出力例 2

5

S = 5 です。ピラミッドは下図の通りになり、C_{1,1} = 5 です。

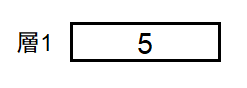
入力例 3

14
11123455678999

出力例 3

913063116

問題文

この問題は インタラクティブ問題 （あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題）です。

以下の条件を共に満たす整数列を non-zero 数列 と呼びます。

• どの 2 つの項も相異なる
• どの空でない (連続とは限らない) 部分列の総和も 0 でない

例えば、(5), (1,-2,3), (-3,7,5,-6) などは non-zero 数列ですが、(0), (1,-3,1), (2,3,-2), (1,2,3,-4) などは non-zero 数列ではありません。

正整数 N, X が与えられます。

-N 以上 N 以下の整数からなる長さ X(=2 \lfloor \sqrt N \rfloor - 1) の non-zero 数列 (A_1, A_2, \dots, A_X) を前から順に 1 項ずつ出力してください。ただし、各項の正負は直前に指定されます。

R 個のテストケースが与えられるので、それぞれについてやり取りを行ってください。

制約

• 1\leq R \leq 10^4
• 1\leq N \leq 10^4
• X=2 \lfloor \sqrt N \rfloor - 1
• R 個のテストケースにおける N の総和は 10^4 以下

入出力

この問題はインタラクティブ問題（あなたの作成したプログラムとジャッジシステムが入出力を介して対話を行う形式の問題）です。 最初に、テストケースの数 R を標準入力から受け取ってください。

R

その後、以下のやりとりを R 回繰り返してください。 各テストケースでは、まず正整数 N,X が与えられます。

N X

その後、各 i = 1, 2, \dots, X について、この順に次のやりとりを行ってください。

まず、A_i の符号 \text{op}_i が与えられます。

\text{op}_i

\text{op}_i は +, -, ! のいずれかで、それぞれ以下を表します。

• \text{op}_i = + のとき、A_i が正の整数でなければならないことを表します。
• \text{op}_i = - のとき、A_i が負の整数でなければならないことを表します。
• \text{op}_i = ! のとき、あなたのプログラムが不正解と判定されたことを表します。この場合、ただちにプログラムを終了してください。

その後、-N 以上 N 以下であって、指定された符号の整数 A_i を 1 行に出力してください。（正の整数の出力に符号を付ける必要はありません。）

A_i

出力した (A_1, A_2, \dots, A_X) は non-zero 数列になっていなければなりません。

注意点

• 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
• 実行時間・使用メモリはジャッジプログラムとあなたのプログラムの合計で計測されます。ジャッジプログラムは最大で 100 ms・ 5 MiB 程度を消費します。

入出力例

問題文

整数 H, W, A, B, C, D が与えられます。

H 行 W 列のマス目があります。上から i 行目、左から j 列目のマスをマス (i, j) と呼びます。

各マスは白または黒で塗られており、マス (i, j) の色は、A \le i \le B かつ C \le j \le D を満たすとき黒、そうでないとき白です。

このマス目のいくつかの白マスに照明を配置します。白マス (i, j) に置かれた照明は、以下の 2 つの条件を満たす白マスすべてを照らします。

• マス (i, j) と同じ行または同じ列にある
• マス (i, j) とそのマスの間に黒マスが存在しない

照明の配置は、以下の 2 つの条件を満たすとき valid であると言います。

• すべての白マスが、少なくとも 1 つの照明に照らされている
• 照明のあるマスはいずれも、他の照明によって照らされていない

valid な照明の配置の個数を 998244353 で割ったあまりを求めてください。

制約

• 入力はすべて整数
• 1 \leq A \leq B \leq H \leq 5 \times 10^{5}
• 1 \leq C \leq D \leq W \leq 5 \times 10^{5}
• (A, B) \neq (1, H)
• (C, D) \neq (1, W)

入力例 1

3 3 2 2 2 2

出力例 1

7

valid な照明の配置は以下の 7 通りです。

ただし、下図では照明及び照明に照らされている白マスは緑色で表しています。

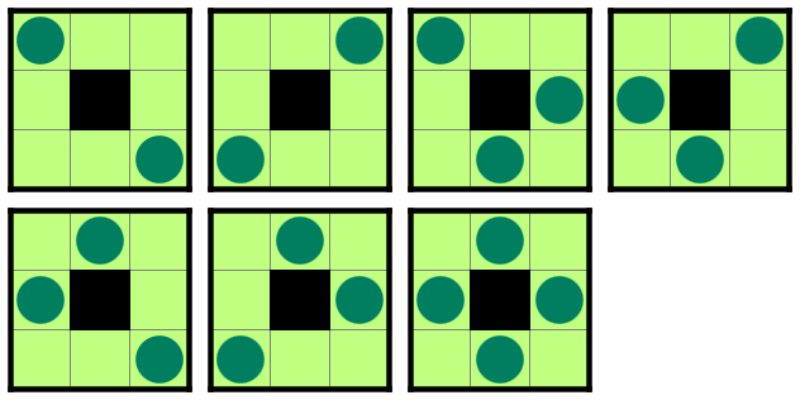
また、以下のような照明の配置は条件を満たしません。

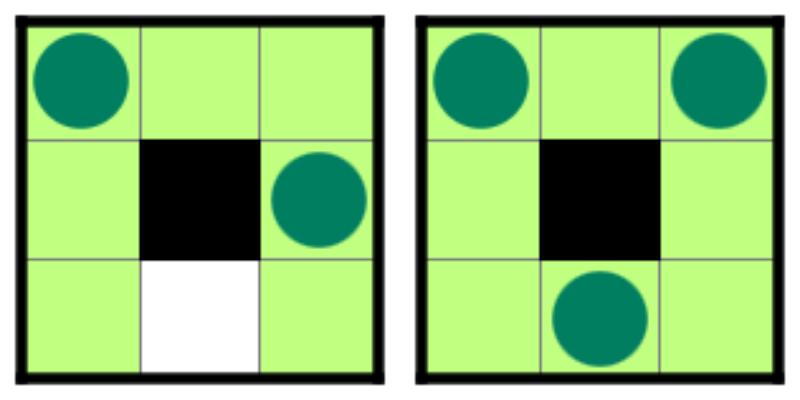
左図の場合、照明に照らされていない白マスがあるため、条件を満たしません。

右図の場合、照明のある白マスであって、他の照明によって照らされているものがあるため、条件を満たしません。

入力例 2

2 3 1 1 1 2

出力例 2

3

入力例 3

500000 500000 100000 200000 100000 250000

出力例 3

360665510

998244353 で割ったあまりを出力してください。

注意

この問題のメモリ制限は 384 MiB です。

問題文

2N+1 行 2N+1 列のグリッドが与えられます。ここで、 N は正整数です。グリッドの上から i 行目、左から j 列目のマス (1 \le i, j \le 2N + 1) をマス (i, j) と表記します。マス (i, j) には文字 S_{i,j} が書かれており、次の性質を満たします。

• i が奇数、 j が奇数であるとき、 S_{i, j} = o
• i が奇数、 j が偶数であるとき、 S_{i, j} = - または .
• i が偶数、 j が奇数であるとき、 S_{i, j} = | または .
• i が偶数、 j が偶数であるとき、 S_{i, j} = .

独立したクエリが Q 個与えられます。 i 個目 (1 \le i \le N) のクエリでは、奇数 U_i, D_i, L_i, R_i (1 \le U_i \le D_i \le 2N+1,\ 1 \le L_i \le R_i \le 2N+1) が与えられるので、次の問いに答えてください。

部分グリッド [U_i, D_i] \times [L_i, R_i] において、文字 o を頂点、文字 - と | を辺としたときにできる無向グラフの連結成分の個数を求めてください。

厳密には、次に問いに答えてください。

((D_i - U_i + 2) / 2) \times ((R_i - L_i + 2) / 2) 頂点の無向グラフ G があり、頂点は U_i 以上 D_i 以下の奇数 x と L_i 以上 R_i 以下の奇数 y のペア (x, y) で表されるとします。また、無向グラフ G には次の無向辺があるとし、これら以外の無向辺はないとします。

• 奇数 x, y が U_i \le x \le D_i,\ L_i \le y \le R_i - 2 かつ S_{x,y+1} = - を満たすならば、頂点 (x, y) と頂点 (x, y+2) との間に無向辺がある。
• 奇数 x, y が U_i \le x \le D_i - 2,\ L_i \le y \le R_i かつ S_{x+1,y} = | を満たすならば、頂点 (x, y) と頂点 (x+2, y) との間に無向辺がある。

無向グラフ G の連結成分の個数を求めてください。

制約

• N は整数
• 1 \le N \le 2000
• i が奇数、j が奇数であるとき、 S_{i, j} = o
• i が奇数、j が偶数であるとき、 S_{i, j} = - または .
• i が偶数、j が奇数であるとき、 S_{i, j} = | または .
• i が偶数、j が偶数であるとき、 S_{i, j} = .
• Q は整数
• 1 \le Q \le 7000
• 1 \le U_i \le D_i \le 2N+1
• 1 \le L_i \le R_i \le 2N+1
• U_i, D_i, L_i, R_i は奇数

入力例 1

3
o-o-o-o
|.....|
o-o.o.o
|.|....
o-o.o-o
....|.|
o.o-o-o
12
3 5 1 7
1 1 1 1
1 3 1 3
1 3 1 7
1 1 1 1
1 1 1 7
1 7 1 1
1 7 1 7
3 5 3 5
3 5 3 7
3 7 3 7
5 7 3 5

出力例 1

4
1
1
2
1
1
2
4
3
4
4
2

与えられるグリッドは次のようになっています。

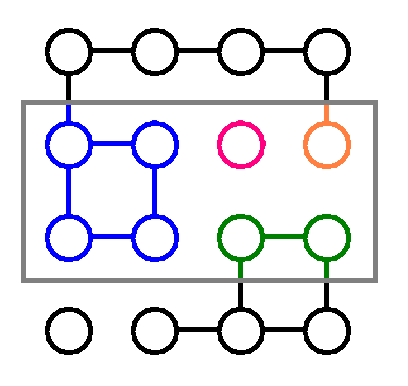
1 番目のクエリにおける答えは、次の図のように 4 となります。

問題文

正整数 N と、大きさ M の整数の集合 S = \lbrace S_{1}, S_{2}, \dots , S_{M} \rbrace が与えられます。

k = 0, 1, \dots , N - 3 について、以下の問題に答えてください。

頂点に 1, 2, \dots, N の番号が付けられた正 N 角形に、k 本の対角線を頂点以外で互いに交わらないように引きます。 このとき、対角線によって正 N 角形は k + 1 個の多角形に分割されます。これらの分割された多角形の辺の数をそれぞれ e_{1}, e_{2}, \dots, e_{k + 1} とします。

ここで、k 本の対角線の引き方が良い引き方であるとは、以下の条件を満たすことを言います。

• e_{1}, e_{2}, \dots ,e_{k + 1} がすべて S に含まれる。

k 本の対角線の良い引き方の個数を 998244353 で割ったあまりを求めてください。

制約

• 入力はすべて整数
• 3\leq N\leq 10^{5}
• 1\leq M\leq N - 2
• 3\leq S_{i}\leq N
• S_{i} < S_{i + 1}

入力例 1

5 2
3 4

出力例 1

0
5
5

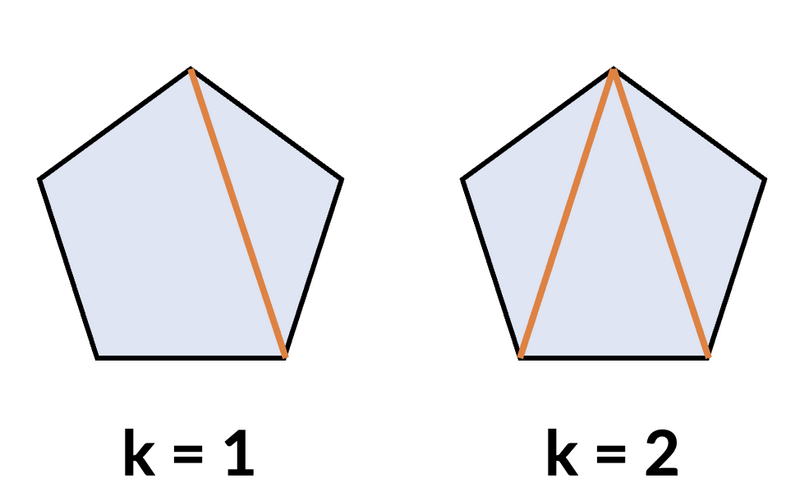
k = 0 のとき、必ず e_{1} = 5 となります。5 は S に含まれていないため、答えは 0 となります。

k = 1 のとき、必ず \{e_{1}, e_{2}\} = \{3, 4\} となり、どちらも S に含まれます。正 5 角形に対角線を 1 本引く方法が 5 通りあるので、答えは 5 となります。

k = 2 のとき、必ず e_{i} = 3 \;(1\leq i\leq 3) となります。正 5 角形に対角線を互いに交わらないように 2 本引く方法が 5 通りあるので、答えは 5 となります。

入力例 2

4 1
4

出力例 2

1
0

入力例 3

16 7
3 4 6 7 9 12 16

出力例 3

1
24
544
14280
120156
829464
3372120
10914816
24515700
40532624
52300160
42493880
17383860
2674440

問題文

2 つのプログラム Alice, Bob が協力して以下のゲームを行います。

0 以上 2^{64} 未満の整数 A, B があります。はじめ Alice のみが A を、Bob のみが B を知っています。

C := \min(A, B) とします。ゲームの目的は、Alice と Bob の両方が C の値を答えられるようにすることです。

そのために、Alice と Bob は以下の関数を何度でも呼び出して情報をやりとりすることができます。

• send(x) : 相手のプログラムが receive() を呼び出すまで待機する。その後、 1 bit の値 x を相手に送信する。
• receive() : 相手のプログラムが send() を呼び出すまで待機する。その後、 1 bit の値 x を相手から受け取って返り値とする。

情報のやり取りが終了した後、各プログラムは以下の関数を 1 度呼び出して C の値を回答する必要があります。

• answer(x) : C の値が x であると回答する。この関数を呼び出した後、ただちにプログラムを終了しなければならない。

Alice と Bob の両方が正しく C の値を回答したらゲームは成功となります。このとき、関数 send() の呼び出し回数の合計が少ないほど良い評価が得られます。

できるだけ少ない回数の関数の呼び出しでゲームを成功させるような 2 つのプログラム Alice, Bob を作成してください。

入出力

この問題はインタラクティブ問題（あなたの作成したプログラムとジャッジプログラムが入出力を介して対話を行う形式の問題）です。
Alice として振る舞うあなたのプログラムと、Bob として振る舞うあなたのプログラムが、ジャッジプログラムを介してゲームを行います。

プログラムの開始

あなたのプログラムは、まず以下の形式で入力を受け取ってください。

\text{Player}
X

ここで、\text{Player} は文字列 Alice または文字列 Bob であり、X は 0 以上 2^{64} 未満の整数です。

• \text{Player} = {}Alice である場合、A = X であることを表します。また、あなたのプログラムはこれ以降 Alice として振る舞わなければなりません。
• \text{Player} = {}Bob である場合、B = X であることを表します。また、あなたのプログラムはこれ以降 Bob として振る舞わなければなりません。

その後、以下に示す方法で send(), receive(), answer() の呼び出しを行ってください。

send

send 関数を呼び出すには、以下の形式で出力してください。

send x

ここで、x は 0 または 1 でなければなりません。
この関数は相手のプログラムが receive() を呼び出すまで待機しますが、待機中に相手のプログラムが停止したり、相手も send 関数を呼び出すと WA になります。

receive

receive 関数を呼び出すには、以下の形式で出力してください。

receive

その後、相手のプログラムから送られた値 x を以下の形式で読み取ってください。

x

この関数は相手のプログラムが send() を呼び出すまで待機しますが、待機中に相手のプログラムが停止したり、相手も receive 関数を呼び出すと WA になります。
やり取りの途中で WA となった場合、与えられる入力は -1 になります。この場合、ただちにプログラムを終了してください。

answer

answer 関数を呼び出すには、以下の形式で出力してください。

answer x

ここで、x は \min(A, B) と一致していなければなりません。この関数を呼び出した後は、ただちにプログラムを終了してください。

得点

あるテストケースにおける、2 つのプログラムの send() の呼び出し回数の合計を Q' とします。この問題のすべてのテストケースにわたる Q' の最大値を Q として、

• Q ≤ 76 のとき 100 点
• 76 < Q ≤ 128 のとき \left\lfloor 100 - 27 \cdot \ln(\frac{Q-74}{2})\right\rfloor 点
• Q > 128 のとき 0 点（WA になります）

が与えられます。

注意点

• 出力を行うたびに、末尾に改行を入れて標準出力を flush してください。そうしなかった場合、ジャッジ結果が TLE となる可能性があります。
• ジャッジプログラムと、Alice として振る舞うあなたのプログラムと、Bob として振る舞うあなたのプログラムが同時に実行されます。実行時間・使用メモリはこれらの合計で計測されるため、実行時間・使用メモリには余裕を持ってください。
  • ジャッジプログラムは最大で 50 ms・5 MiB 程度を消費します。
• この問題では、実行中にファイルを作成することができません。したがって、実行中にファイルを作成するような言語・プログラムでは AC を取ることができません。 例えば、C# では AC を取ることができないため、代わりに C# AOT を使用してください。
• 0 以上 2^{64} 未満の整数を扱います。オーバーフローには十分注意してください。

入出力例

問題文

2 次元平面上に相異なる N 個の点があり、それぞれ 1 から N までの番号が付けられています。点 i の座標は (x_i, y_i) です。

また、それぞれの点には色が付けられています。色の種類は N 個あり、それぞれ 1 から N までの番号が付けられています。点 i の色は c_i です。

あなたは、これらの点から色の相異なる 4 点を選び、任意の順でつないで 1 つの四角形を作ります。この四角形はちょうど 180 度の内角を持っていても構いませんが、連続しないどの 2 辺も共通部分を持ってはいけません。

そのように四角形を作ることができるかどうか判定し、できる場合はその四角形の面積としてあり得る最大値を S として 2S を出力してください。できない場合は 0 を出力してください。

T 個のテストケースが与えられるので、それぞれについて解いてください。

制約

• 入力はすべて整数
• 1\le T\le 10^4
• 4\le N\le 10^5
• |x_i|,|y_i|\le 10^8
• 1\le c_i\le N
• i\neq j ならば (x_i,y_i)\neq (x_j,y_j)
• T 個のテストケースに渡る N の総和は 10^5 以下

入力例 1

4
6
2 4 1
5 4 2
6 2 3
5 1 1
2 1 2
1 3 4
4
1 1 1
3 5 2
7 2 3
4 3 4
5
0 0 1
0 1 2
1 0 2
0 2 3
2 0 3
4
0 0 1
0 100000000 2
100000000 0 3
100000000 100000000 4

出力例 1

15
17
0
20000000000000000

1 番目のテストケースでは、点 1,2,3,6 をこの順でつないでできる四角形は条件を満たしており、その面積は 15/2 です。この四角形は条件を満たす四角形のうち面積が最大です。点 1,2,4,5 をこの順でつないでできる四角形の面積は 9 ですが、点 1,4 の色は同じなので、この四角形は条件を満たしていません。

2 番目のテストケースでは、条件を満たす四角形を作ることができますが、凸であるものを作ることはできません。

3 番目のテストケースでは、条件を満たす四角形を作ることはできません。

4 番目のテストケースのように、答えが非常に大きくなる場合があることに注意してください。

問題文

N 個の広場が左右一列に並んだ公園があり、広場には左から順に 0,1,\dots, N-1 の番号が付けられています。

公園の中に、0, 1, \dots, N-1 の番号が付けられた N 人の人がいます。あなたが 0 以上 N-1 以下の非負整数の列 X=(X_1,X_2,\dots, X_{|X|}) を宣言すると、これらの人々は次のように 行進 を行います。

1. 各 i = 0,1,\dots, N-1 について、人 i が広場 i に移動する。
2. 各 j = 1, 2, \dots, |X| について、この順に以下を行う。
   • 広場 X_j 以外の広場にいるすべての人は、自身のいる広場から広場 X_j に向けて広場 1 つ分だけ移動する。

0 以上 N-1 以下の非負整数からなる長さ M の列 A=(A_0,A_1,\dots, A_{M-1}) が与えられます。

Q 個のクエリにオンラインで答えてください。 i=1,2,\dots, Q について、 i 番目のクエリでは整数 t_i',L_i',R_i',P_i' が与えられます。まず、次の手順で t_i,L_i,R_i,P_i を復元してください。

• \mathrm{ans}_0=0 、\mathrm{ans}_i= ( i 番目のクエリの答え) とする。
• このとき、次のように t_i,L_i,R_i,P_i を復元する。
  • t_i=((t_i' + \mathrm{ans}_{i-1})\bmod 2)
  • a=((L_i' + \mathrm{ans}_{i-1})\bmod M)
  • b=((R_i' + \mathrm{ans}_{i-1})\bmod M)
  • L_i=\min(a,b)
  • R_i=\max(a,b)
  • P_i=((P_i' + \mathrm{ans}_{i-1})\bmod N)

ここで非負整数 a と正整数 b に対して (a\bmod b) は a を b で割ったあまりを表します。この値は 0 以上 b 未満です。

このようにして得られた t_i,L_i,R_i,P_i に対して、次のクエリに答えてください。

• t_i=0 の場合： X = (A_{L_i},A_{L_i+1}\dots, A_{R_i}) を宣言して行進を行うときの、最終的に人 P_i がいる広場の番号を答えてください。
• t_i=1 の場合： X = (A_{L_i},A_{L_i+1}\dots, A_{R_i}) を宣言して行進を行うときの、最終的に広場 P_i にいる人数を答えてください。

制約

• 入力はすべて整数
• 1\le N,M,Q\le 2\times 10^5
• 0\le A_i\le N-1\ (0\le i\le M-1)
• 0\le t_i',t_i\le 1\ (1\le i\le Q)
• 0\le L_i',R_i'\le M-1\ (1\le i\le Q)
• 0\le L_i\le R_i\le M-1\ (1\le i\le Q)
• 0\le P_i',P_i\le N-1\ (1\le i\le Q)

入力例 1

4 5 3
0 2 3 2 1
0 1 3 2
1 0 2 1
1 4 4 1

出力例 1

2
0
3

1 番目のクエリでは (t_i,L_i,R_i,P_i)=(0,1,3,2) です。 X = (A_1,A_2,A_3)=(2,3,2) を宣言して行進を行ったとき、人 2 は広場を 2\to 2\to 3\to 2 の順に移動します。よって答えは 2 です。

2 番目のクエリでは (t_i,L_i,R_i,P_i)=(1,2,4,3) です。 X = (A_2,A_3,A_4)=(3,2,1) を宣言して行進を行ったとき、最終的に各広場にいる人の人数は広場 0 から順に 0,4,0,0 です。よって答えは 0 です。

3 番目のクエリでは (t_i,L_i,R_i,P_i)=(1,4,4,1) です。 X = (A_4)=(1) を宣言して行進を行ったとき、最終的に各広場にいる人の人数は広場 0 から順に 0,3,1,0 です。よって答えは 3 です。

入力例 2

7 4 1
3 3 3 3
1 3 0 3

出力例 2

7