Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 9 点
問題文
うさぎとかめが競走をしています。先に X メートル走った方の勝ちです。
うさぎは秒速 A メートル、かめは秒速 B メートルで走ります。
しかし、うさぎはスタートしてから \frac{X}{2} メートル走った時点で、その場で C 秒間立ち止まって眠ってしまいます。C 秒間経過すると、うさぎは目を覚まして再び秒速 A メートルで走ります。
レースの勝者を求めてください。ただし、同時にゴールする場合はその旨を出力してください。
制約
- 1 \leq X \leq 10000
- 1 \leq A, B \leq 100
- 1 \leq C \leq 10000
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
X A B C
出力
うさぎが勝つなら Hare、かめが勝つなら Tortoise、両者が同時にゴールするなら Tie と出力せよ。
入力例 1
100 5 3 15
出力例 1
Tortoise
うさぎは 10 秒かけて 50 メートル走り、15 秒眠ったのち、再び 10 秒かけて 50 メートル走ります。合計 35 秒かけてゴールします。
かめは \frac{100}{3} 秒かけてゴールします。
\frac{100}{3} \lt 35 より、かめが勝利します。
入力例 2
240 6 2 80
出力例 2
Tie
両者は同時にゴールします。
入力例 3
10000 100 1 1000
出力例 3
Hare
Score : 9 points
Problem Statement
A hare and a tortoise are in a race. The first to run X meters wins.
The hare runs A meters per second, and the tortoise runs B meters per second.
However, at \frac{X}{2} meters from the start, the hare stops running and sleeps for C seconds. Then, it wakes up and continues running A meters per second.
Find the winner of the race. If the two finish simultaneously, report that fact.
Constraints
- 1 \leq X \leq 10000
- 1 \leq A, B \leq 100
- 1 \leq C \leq 10000
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
X A B C
Output
If the hare wins, print Hare; if the tortoise wins, print Tortoise; if the two finish simultaneously, print Tie.
Sample Input 1
100 5 3 15
Sample Output 1
Tortoise
The hare runs 50 meters in 10 seconds, sleeps for 15 seconds, and again runs 50 meters in 10 seconds, for a total of 35 seconds.
The tortoise finishes the race in \frac{100}{3} seconds.
We have \frac{100}{3} \lt 35, so the tortoise wins.
Sample Input 2
240 6 2 80
Sample Output 2
Tie
The two finish simultaneously.
Sample Input 3
10000 100 1 1000
Sample Output 3
Hare
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 8 点
問題文
英小文字のみからなる文字列 S が与えられます。
1 \le i \le |S|-1 を満たす全ての整数 i について、 S の i 文字目と i+1 文字目をこの順に連結した 2 文字の文字列を書き並べます。
このとき、最も多く書かれる文字列を求めてください。ただし、そのようなものが複数存在する場合、辞書順最小のものを求めてください。
制約
- 2 \le |S| \le 2 \times 10^5
- S は英小文字のみからなる。
入力
入力は以下の形式で標準入力から与えられる。
S
出力
答えを出力せよ。
入力例 1
abcab
出力例 1
ab
書き並べられる文字列は ab, bc, ca, ab です。
最も多く書かれる文字列は ab です。
入力例 2
zyxwv
出力例 2
wv
入力例 3
iiiiiiiiiiiiiiiiiiiiiiiiiiiiii
出力例 3
ii
Score : 8 points
Problem Statement
You are given a string S consisting of lowercase English letters.
Now you will write, for every integer i such that 1 \le i \le |S|-1, a two-letter string obtained by concatenating the i-th and the (i+1)-th characters of S.
Find the string that you will write the most times. If there are multiple such strings, find the lexicographically smallest one.
Constraints
- 2 \le |S| \le 2 \times 10^5
- S consists of lowercase English letters.
Input
Input is given from Standard Input in the following format:
S
Output
Print the answer.
Sample Input 1
abcab
Sample Output 1
ab
You will write ab, bc, ca, and ab.
Among them, ab is written the most times.
Sample Input 2
zyxwv
Sample Output 2
wv
Sample Input 3
iiiiiiiiiiiiiiiiiiiiiiiiiiiiii
Sample Output 3
ii
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 8 点
問題文
整数 N, M に対して、文字列 S_{N,M} を以下のように定義します。
- S_{N,M} は
oとxからなる長さ M の文字列である。 - S_{N,M} の前から k 文字目は、N^k≤10^9 であれば
o、そうでなければxである。
整数 N, M が与えられるので、S_{N,M} を出力してください。
制約
- N, M は整数である。
- 1≤N≤10^9
- 1≤M≤10^5
入力
入力は以下の形式で標準入力から与えられる。
N M
出力
S_{N,M} を出力せよ。
入力例 1
1000 5
出力例 1
oooxx
S_{1000,5} は以下のように求められます。
- 前から 1 文字目は、1000^1=10^3≤10^9 であるから、
oである。 - 前から 2 文字目は、1000^2=10^6≤10^9 であるから、
oである。 - 前から 3 文字目は、1000^3=10^9≤10^9 であるから、
oである。 - 前から 4 文字目は、1000^4=10^{12}>10^9 であるから、
xである。 - 前から 5 文字目は、1000^5=10^{15}>10^9 であるから、
xである。
入力例 2
2 30
出力例 2
ooooooooooooooooooooooooooooox
入力例 3
31622 30
出力例 3
ooxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Score : 8 points
Problem Statement
For integers N and M, let us define S_{N,M} as follows.
- S_{N,M} is a string of length M consisting of
oandx. - The k-th character from the beginning of S_{N,M} is
oif N^k≤10^9 andxotherwise.
Given the integers N and M, print S_{N,M}.
Constraints
- N and M are integers.
- 1≤N≤10^9
- 1≤M≤10^5
Input
Input is given from Standard Input in the following format:
N M
Output
Print S_{N,M}.
Sample Input 1
1000 5
Sample Output 1
oooxx
S_{1000,5} is found as follows.
- The 1-st character from the beginning is
obecause 1000^1=10^3≤10^9. - The 2-nd character from the beginning is
obecause 1000^2=10^6≤10^9. - The 3-rd character from the beginning is
obecause 1000^3=10^9≤10^9. - The 4-th character from the beginning is
xbecause 1000^4=10^{12}>10^9. - The 5-th character from the beginning is
xbecause 1000^5=10^{15}>10^9.
Sample Input 2
2 30
Sample Output 2
ooooooooooooooooooooooooooooox
Sample Input 3
31622 30
Sample Output 3
ooxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 7 点
問題文
英小文字の組 (a_1,b_1),(a_2,b_2),\dots,(a_N,b_N) があります。
英小文字 u,v が 似ている とは、(u,v)=(a_i,b_i) または (u,v)=(b_i,a_i) を満たす i が存在することを言います。
また、長さの等しい英小文字からなる文字列 U,V が 似ている とは、U,V が次の条件を満たすことを言います。
- U の文字を 1 つ選んで、似ている文字に置き換えることを好きなだけ繰り返したとき(操作をしなくてもよい)、V に一致させることができる。
長さの等しい文字列 S,T が与えらえるので、S と T が似ているか判定してください。
制約
- 1 \leq N \leq 325
- N は整数である。
- a_i,b_i は互いに異なる英小文字である。
- i \neq j ならば (a_i,b_i) \neq (a_j,b_j) かつ (a_i,b_i) \neq (b_j,a_j) が成り立つ。
- S,T は英小文字からなる長さ 1 以上 100 以下の文字列である。
- S の長さと T の長さは等しい。
入力
入力は以下の形式で標準入力から与えられる。
N a_1 b_1 a_2 b_2 \vdots a_N b_N S T
出力
S と T が似ているならば Yes を、そうでないならば No を出力せよ。
入力例 1
1 m n man nan
出力例 1
Yes
S の 1 文字目を m から n に置き換えて nan にすることで、S を T と一致させることができます。m と n は似ている文字なので、S と T は似ている文字列の条件を満たします。
入力例 2
1 m n man men
出力例 2
No
入力例 3
3 a b a e d e abc edc
出力例 3
Yes
入力例 4
1 a b xyz xyz
出力例 4
Yes
Score : 7 points
Problem Statement
We have pairs of lowercase English letters (a_1,b_1),(a_2,b_2),\dots,(a_N,b_N).
Two lowercase English letters u and v are said to be similar if there exists i such that (u,v)=(a_i,b_i) or (u,v)=(b_i,a_i).
Two strings U and V with the same length are said to be similar if U and V satisfy the following condition:
- You can make U equal V by repeatedly (possibly zero times) choosing one of the characters of U and replacing it with a similar character.
Given strings S and T with the same length, determine if S and T are similar.
Constraints
- 1 \leq N \leq 325
- N is an integer.
- a_i and b_i are distinct lowercase English letters.
- If i \neq j, then (a_i,b_i) \neq (a_j,b_j) and (a_i,b_i) \neq (b_j,a_j).
- S and T are strings of length between 1 and 100, inclusive.
- S and T have the same length.
Input
Input is given from Standard Input in the following format:
N a_1 b_1 a_2 b_2 \vdots a_N b_N S T
Output
If S and T are similar, print Yes; otherwise, print No.
Sample Input 1
1 m n man nan
Sample Output 1
Yes
We can make S equal T by replacing the 1-st character of S with n, making S nan. Since m and n are similar characters, S and T satisfy the condition of similar strings.
Sample Input 2
1 m n man men
Sample Output 2
No
Sample Input 3
3 a b a e d e abc edc
Sample Output 3
Yes
Sample Input 4
1 a b xyz xyz
Sample Output 4
Yes
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 7 点
問題文
以下の操作によって構成される数列 A の第 N 項を求めてください。
- 最初、数列 A は空である。
- 1 以上 10^{100} 以下の全ての整数 i について、以下の操作を i の小さい方から行う。
- もし i \ge 2 なら、 i,i-1,\dots,2 を数列の末尾にこの順に追加する。
- その後、 1,2,\dots,i を数列の末尾にこの順に追加する。
制約
- N は整数
- 1 \le N \le 10^{18}
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを整数として出力せよ。
入力例 1
10
出力例 1
4
A=(1,2,1,2,3,2,1,2,3,4,3,2,1,2,3,4,\dots) なので、第 10 項は 4 です。
入力例 2
1
出力例 2
1
入力例 3
123456789012345678
出力例 3
268452372
入力が 32bit 整数に収まらない場合もあります。
Score : 7 points
Problem Statement
Find the N-th term of the sequence A constructed as follows.
- Initially, A is empty.
- For every integer i from 1 through 10^{100} in ascending order, do the following.
- If i \ge 2, append i,i-1,\dots,2 in this order to the end of A.
- Then, append 1,2,\dots,i in this order to the end of A.
Constraints
- N is an integer.
- 1 \le N \le 10^{18}
Input
Input is given from Standard Input in the following format:
N
Output
Print the answer as an integer.
Sample Input 1
10
Sample Output 1
4
We have A=(1,2,1,2,3,2,1,2,3,4,3,2,1,2,3,4,\dots), where the 10-th term is 4.
Sample Input 2
1
Sample Output 2
1
Sample Input 3
123456789012345678
Sample Output 3
268452372
Input may not fit into a 32-bit integer.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 7 点
問題文
高橋君はシューティングゲームで遊んでいます。ゲーム画面は H 行 W 列のグリッドであり、上から i \, (1 \leq i \leq H) 行目、左から j \, (1 \leq j \leq W) のマスを (i, j) と表します。各マスは空マスまたはブロックマスであり、ブロックマスには正の整数で表される色が付けられています。
マス (i, j) の情報は非負整数 S_{i, j} で表されます。S_{i,j} = 0 ならそのマスは空マスであり、S_{i, j} が正の整数ならそのマスは色 S_{i, j} のブロックマスです。
また、H 行目以外に存在するブロックマスであって、下に隣接するマスが空マスであるようなものを空中ブロックと呼びます。はじめ、空中ブロックは存在しません。
高橋君はこれから N 回の操作を行います。i \, (1 \leq i \leq N) 回目の操作は以下の通りです。
- マス (r_i, c_i) を撃つ。そのマスが空マスなら何も起こらず、ブロックマスならそのマスは空マスに変化する。
- その後、全ての空中ブロックが落下する。厳密には、以下の操作を空中ブロックが存在しなくなるまで行う。
- 空中ブロックを一つ選び、そのマスと下に隣接するマスを入れ替える。
N 回の操作が終わった後の各マスの情報を S_{i, j} と同様の方法で出力してください。
制約
- 1 \leq H, W \leq 100
- 0 \leq S_{i, j} \leq 10^9 \, (1 \leq i \leq H, 1 \leq j \leq W)
- S_{i, j} > 0 ならば S_{i + 1, j} > 0 \, (1 \leq i \leq H - 1, 1 \leq j \leq W)
- 1 \leq N \leq 10^3
- 1 \leq r_i \leq H \, (1 \leq i \leq N)
- 1 \leq c_i \leq W \, (1 \leq i \leq N)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
H W
S_{1, 1} \ldots S_{1, W}
\vdots
S_{H, 1} \ldots S_{H, W}
N
r_1 c_1
\vdots
r_N c_N
出力
H 行にわたって出力せよ。各行には W 個の整数を、以下の条件を満たすように空白区切りで出力せよ。
- i \, (1 \leq i \leq H) 行目の j \, (1 \leq j \leq W) 個目の整数は、高橋君の N 回の操作が全て終了した後のマス (i, j) が空マスなら 0 であり、ブロックマスならその色を表す正の整数である。
入力例 1
3 3 0 1 0 1 2 0 3 4 4 1 3 2
出力例 1
0 0 0 1 1 0 3 2 4
マス (3, 2) を撃つと、ゲーム画面は次のように変化します。
0 1 0 \quad 0 1 0 \quad 0 1 0 \quad 0 0 0 1 2 0 \rightarrow 1 2 0 \rightarrow 1 0 0 \rightarrow 1 1 0 3 4 4 \quad 3 0 4 \quad 3 2 4 \quad 3 2 4
入力例 2
1 1 1 1 1 1
出力例 2
0
入力例 3
2 3 18459 0 35959 150312 573935 612940 3 2 3 1 2 1 1
出力例 3
0 0 0 150312 573935 35959
Score : 7 points
Problem Statement
Takahashi is playing with a shooter video game. The game screen has a grid with H horizontal rows and W vertical columns. The square at the i-th (1 \leq i \leq H) row from the top and j-th (1 \leq j \leq W) column from the left in the grid is called (i, j). Each square is either an empty square or a brick square. Each brick square is painted in the color represented by a positive integer.
The state of Square (i, j) is expressed by a non-negative integer S_{i, j}. If S_{i,j} = 0, then the square is an empty square; if S_{i, j} is a positive integer, then the square is a brick square of color S_{i, j}.
Let us call a brick square in the row other than the H-th row from the top a floating brick if the adjacent square below is an empty square. Initially, there is no floating brick.
Now, Takahashi will do N operations, the i-th (1 \leq i \leq N) of which is as follows:
- Shoot Square (r_i, c_i). If the square is an empty square, nothing happens; if it is a brick square, it changes to an empty square.
- Then, all the floating bricks fall. Strictly speaking, the following operation is performed until there is no floating brick:
- Choose one floating brick and swap that square with the adjacent square below.
Print the state of each square after the N operations have finished, in the same format as S_{i, j}.
Constraints
- 1 \leq H, W \leq 100
- 0 \leq S_{i, j} \leq 10^9 \, (1 \leq i \leq H, 1 \leq j \leq W)
- If S_{i, j} > 0, then S_{i + 1, j} > 0 \, (1 \leq i \leq H - 1, 1 \leq j \leq W).
- 1 \leq N \leq 10^3
- 1 \leq r_i \leq H \, (1 \leq i \leq N)
- 1 \leq c_i \leq W \, (1 \leq i \leq N)
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
H W
S_{1, 1} \ldots S_{1, W}
\vdots
S_{H, 1} \ldots S_{H, W}
N
r_1 c_1
\vdots
r_N c_N
Output
Print H lines. Each line should contain W integers separated by spaces so that the following condition is satisfied:
- The j-th (1 \leq j \leq W) integer in the i-th (1 \leq i \leq H) line should be 0 if Square (i, j) is an empty square after Takahashi's N operations have completed; if it ends up a brick square, it should be the integer representing its color.
Sample Input 1
3 3 0 1 0 1 2 0 3 4 4 1 3 2
Sample Output 1
0 0 0 1 1 0 3 2 4
When he shoots Square (3, 2), the grid transitions as follows:
0 1 0 \quad 0 1 0 \quad 0 1 0 \quad 0 0 0 1 2 0 \rightarrow 1 2 0 \rightarrow 1 0 0 \rightarrow 1 1 0 3 4 4 \quad 3 0 4 \quad 3 2 4 \quad 3 2 4
Sample Input 2
1 1 1 1 1 1
Sample Output 2
0
Sample Input 3
2 3 18459 0 35959 150312 573935 612940 3 2 3 1 2 1 1
Sample Output 3
0 0 0 150312 573935 35959
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
N 頂点 N-1 辺の無向グラフが与えられます。i \, (1 \leq i \leq N-1) 番目の辺は頂点 A_i と頂点 B_i を結んでいます。
与えられるグラフが木かどうか判定してください。
制約
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i \lt B_i \leq N
- (A_i, B_i) \neq (A_j, B_j) \, (i \neq j)
- 入力は全て整数である。
入力
入力は以下の形式で標準入力から与えられる。
N
A_1 B_1
\vdots
A_{N-1} B_{N-1}
出力
与えられるグラフが木なら Yes と、木でないなら No と出力せよ。
入力例 1
4 1 3 3 4 2 3
出力例 1
Yes
与えられるグラフは下図の通りです。
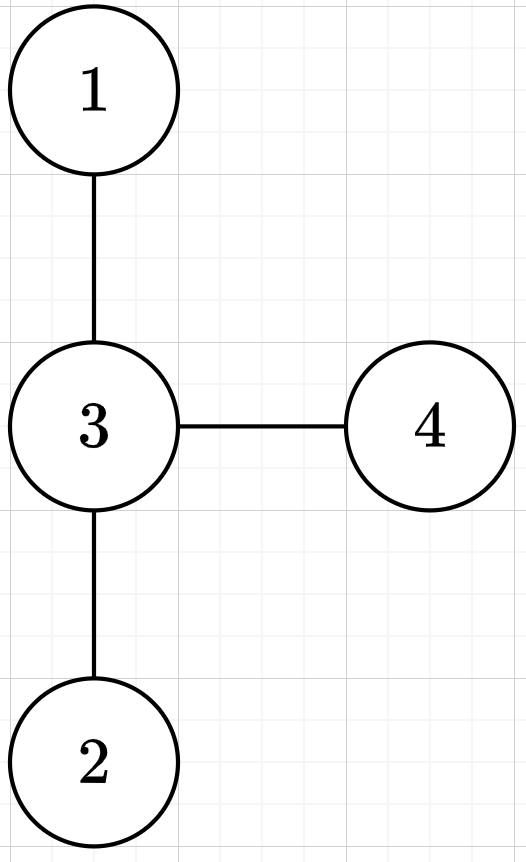
入力例 2
4 1 2 2 3 1 3
出力例 2
No
与えられるグラフは下図の通りです。

Score : 6 points
Problem Statement
You are given an undirected graph with N vertices and N-1 edges. The i-th (1 \leq i \leq N-1) edge connects Vertex A_i and Vertex B_i.
Determine whether the given graph is a tree.
Constraints
- 2 \leq N \leq 2 \times 10^5
- 1 \leq A_i \lt B_i \leq N
- (A_i, B_i) \neq (A_j, B_j) \, (i \neq j)
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N
A_1 B_1
\vdots
A_{N-1} B_{N-1}
Output
If the given graph is a tree, print Yes; otherwise, print No.
Sample Input 1
4 1 3 3 4 2 3
Sample Output 1
Yes
The figure below illustrates the given graph.

Sample Input 2
4 1 2 2 3 1 3
Sample Output 2
No
The figure below illustrates the given graph.

Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
高橋君は N 個のお菓子を持っています。 i = 1, 2, \ldots, N について、i 番目のお菓子の重さは w_i 、美味しさは v_i です。
高橋君は N 個のうち好きな個数( 0 個でもよい)のお菓子を選んで、明日の遠足に持って行きます。 高橋君は 2 つのナップサックを持っており、遠足に持っていくお菓子はそれぞれ 2 つのナップサックのどちらかに入れなければなりません。 ただし、1 つ目のナップサックに入れるお菓子の重さの合計は A 以下でなければならず、 2 つ目のナップサックに入れるお菓子の重さの合計は B 以下でなければなりません。
高橋君が遠足に持っていくお菓子の美味しさの合計としてありえる最大値を出力してください。
制約
- 1 \leq N \leq 100
- 1 \leq A, B \leq 300
- 1 \leq w_i \leq 300
- 1 \leq v_i \leq 10^9
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A B w_1 v_1 w_2 v_2 \vdots w_N v_N
出力
答えを出力せよ。
入力例 1
6 8 9 2 6 4 1 5 9 3 1 5 3 5 8
出力例 1
24
1 番目のお菓子と 3 番目のお菓子を 1 つ目のナップサックに入れ、
2 番目のお菓子と 6 番目のお菓子を 2 つ目のナップサックに入れます。
このとき、1 つ目のナップサックに入れたお菓子の重さの合計は w_1 + w_3 = 2 + 5 = 7 、
2 つ目のナップサックに入れたお菓子の重さの合計は w_2 + w_6 = 4 + 5 = 9 であり、入れたお菓子の重さの合計は、それぞれのナップサックの上限 A = 8, B = 9 を超えません。
また、遠足に持っていくお菓子の美味しさの合計は、v_1 + v_2 + v_3 + v_6 = 6 + 1 + 9 + 8 = 24 であり、これが最大です。
入力例 2
20 70 60 7 94 18 33 14 26 10 1 9 57 2 80 19 74 16 10 15 18 10 38 13 90 12 23 3 3 8 11 18 10 3 42 3 66 3 90 10 2 5 45
出力例 2
772
Score : 6 points
Problem Statement
Takahashi has N snacks. For i = 1, 2, \ldots, N, the i-th snack has a weight of w_i and a tastiness of v_i.
Takahashi is going to choose any number (possibly 0) of the N snacks to take on tomorrow's school trip. Takahashi has two knapsacks. Every snack he takes on the school trip should fit in one of the two knapsacks. Here, the sum of weights of snacks in the first knapsack should be at most A, and the sum of weights of snacks in the second knapsack should be at most B.
Find the maximum possible total tastiness of snacks that he can take on the school trip.
Constraints
- 1 \leq N \leq 100
- 1 \leq A, B \leq 300
- 1 \leq w_i \leq 300
- 1 \leq v_i \leq 10^9
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N A B w_1 v_1 w_2 v_2 \vdots w_N v_N
Output
Print the answer.
Sample Input 1
6 8 9 2 6 4 1 5 9 3 1 5 3 5 8
Sample Output 1
24
He can put the 1-st and the 3-rd snacks in the first knapsack,
and the 2-nd and the 6-th snacks in the second knapsack.
Then, the sum of weights of the snacks in the first knapsack is w_1 + w_3 = 2 + 5 = 7,
and the sum of the snacks in the second knapsack is w_2 + w_6 = 4 + 5 = 9, which do not exceed the upper limits of the respective knapsacks, A = 8, B = 9.
The total tastiness of the snacks he will take on the school trip is v_1 + v_2 + v_3 + v_6 = 6 + 1 + 9 + 8 = 24, which is the maximum.
Sample Input 2
20 70 60 7 94 18 33 14 26 10 1 9 57 2 80 19 74 16 10 15 18 10 38 13 90 12 23 3 3 8 11 18 10 3 42 3 66 3 90 10 2 5 45
Sample Output 2
772
Time Limit: 4 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
縦 H 行、横 W 列の長方形のマス目が与えられます。上から i 番目、左から j 番目のマスをマス (i,j) と呼びます。
各マスは、「壁のないマス」、「壁があるマス」のいずれかです。マス (i,j) の初期状態の情報は S_{i,j} で表され、以下を意味します。
.:壁のないマスである。s:壁のないマスであり、すぬけ君がいる。a:壁のないマスであり、荷物がある。g:壁のないマスであり、片付け先である。#:壁があるマスであり、通ることができない。
荷物と片付け先のマスはちょうど 1 個ずつあり、すぬけ君はちょうど 1 人であることが保証されます。すぬけ君の目標は荷物を片付け先のマスに運ぶことです。
すぬけ君は以下のいずれかの行動を何回でも行うことができます。
- 今いるマスと上下左右に隣接している、荷物も壁もないマスに移動する。
- 今いるマスと上下左右に隣接しているマスにある荷物を、すぬけ君から見て1つ奥の壁のないマスに押して動かし、動かした荷物があったマスに移動する。
すぬけ君が目標を達成するために必要な行動回数の最小値を出力してください。ただし、目標が達成不可能な場合は -1 を出力してください。
制約
- H,W は 1 以上 50 以下の整数
- S_i は
.,s,a,g,#からなる長さ W の文字列 - S_{i,j} の中に
s,a,gはそれぞれちょうど 1 個ずつ含まれる
入力
入力は以下の形式で標準入力から与えられる。
H W
S_{1,1}S_{1,2}\ldots S_{1,W}
\vdots
S_{H,1}S_{H,2}\ldots S_{H,W}
出力
答えを出力せよ。
入力例 1
3 3 s.. .a. ..g
出力例 1
5
以下のように移動することで 5 回で荷物を片付け先のマスに運べます。
- 右に移動する。
- 荷物を下に押し、下に移動する。
- 左に移動する。
- 下に移動する。
- 荷物を右に押し、右に移動する。
入力例 2
4 4 s... .a#. .... ###g
出力例 2
13
入力例 3
4 4 ...a .s.. ..g. ....
出力例 3
-1
目標を達成不可能な場合、-1 を出力してください。
Score : 6 points
Problem Statement
You are given a rectangular grid with H horizontal rows and W vertical columns. The square at the i-th row from the top and the j-th column from the left is called Sqaure (i, j).
Each square is either a "square without a wall" or a "square with a wall". The initial state of Square (i, j) is represented by S_{i,j}, which means:
.: it is a square without a wall.s: it is a square without a wall, and Snuke is there.a: it is a square without a wall, and there is a cargo in it.g: it is a square without a wall, and is a destination of the cargo.#: it is a square with a wall, which cannot be visited.
It is guaranteed that there is exactly one cargo, one destination, and one Snuke in the grid. Snuke's objective is to carry the cargo to the destination.
Snuke can do one of the following moves any number of times:
- Move to a square, without the cargo or a wall, vertically or horizontally adjacent to Snuke's current square.
- Push the cargo in the square vertically or horizontally adjacent to Snuke's current square to the next square without a wall in the direction of the cargo from Snuke, and move to the square that the cargo was originally in.
Print the minimum number of moves required for Snuke to achieve the objective. If the objective is unachievable, print -1 instead.
Constraints
- H and W are integers between 1 and 50, inclusive.
- S_i is a string of length W consisting of
.,s,a,g, and#. - S_{i,j} contains exactly one
s, onea, and oneg.
Input
Input is given from Standard Input in the following format:
H W
S_{1,1}S_{1,2}\ldots S_{1,W}
\vdots
S_{H,1}S_{H,2}\ldots S_{H,W}
Output
Print the answer.
Sample Input 1
3 3 s.. .a. ..g
Sample Output 1
5
He can carry the cargo with 5 moves by moving as follows:
- Move to the right.
- Push the cargo downward, and move downward.
- Move to the left.
- Move downward.
- Push the cargo to the right, and move to the right.
Sample Input 2
4 4 s... .a#. .... ###g
Sample Output 2
13
Sample Input 3
4 4 ...a .s.. ..g. ....
Sample Output 3
-1
If the objective is unachievable, print -1.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
あなたは、毎週土曜日と日曜日に必ず 1 個ずつりんごを食べます。それ以外の日にはりんごを食べません。
2 つの日付 S,T が YYYY-MM-DD 形式で与えられるので、S から T までの期間(S 及び T も含む)に何個のりんごを食べることにな るか求めてください。
なお、必要であれば、以下の事実を用いても構いません。
- 2022 年 1 月 1 日は土曜日
- 次のいずれかの条件を満たすとき、かつ、そのときに限り X 年はうるう年
- X が 4 の倍数であり、かつ、100 の倍数でない
- X が 400 の倍数
YYYY-MM-DD 形式とは
年を表す 4 桁の整数、月を表す 2 桁の整数、日を表す 2 桁の整数を、この順に - 区切りで繋げたものを YYYY-MM-DD 形式といいます。
ただし、月や日が 1 桁のときは、上位に 0 を付けて 2 桁とします。
例えば、4567 年 1 月 23 日を YYYY-MM-DD 形式で表すと 4567-01-23 となります。
制約
- S,T は 2022 年 1 月 1 日以降 9999 年 12 月 31 日以前の有効な日付を
YYYY-MM-DD形式で表したものである - T は S 以降の日付を表す
入力
入力は以下の形式で標準入力から与えられる。
S T
出力
答えを出力せよ。
入力例 1
2022-01-01 2022-01-08
出力例 1
3
与えられた期間のうち 2022 年 1 月 1,2,8 日にそれぞれりんごを 1 個ずつ食べます。
入力例 2
2024-02-26 2024-03-02
出力例 2
1
うるう年に注意してください。
入力例 3
2022-01-01 9999-12-31
出力例 3
832544
Score : 6 points
Problem Statement
You eat an apple every Saturday and Sunday. You do not eat one any other day.
Given two dates S and T in YYYY-MM-DD format, find the number of apples you eat between S and T (inclusive).
Here are some facts that may be useful.
- January 1, 2022 is Saturday.
- The year X is a leap year if and only if one of the following is satisfied.
- X is a multiple of 4 but not a multiple of 100
- X is a multiple of 400
What is YYYY-MM-DD format?
YYYY-MM-DD format is a concatenation of a 4-digit integer representing the year, a 2-digit integer representing the month, and a 2-digit integer representing the day, in this order, separated by -.
Here, the month and the day are zero-padded to two digits.
For example, January 23, 4567 in YYYY-MM-DD format is 4567-01-23.
Constraints
- S and T are valid dates between January 1, 2022 and December 31, 9999 (inclusive) in
YYYY-MM-DDformat. - T is not earlier than S.
Input
Input is given from Standard Input in the following format:
S T
Output
Print the answer.
Sample Input 1
2022-01-01 2022-01-08
Sample Output 1
3
During the given period, you eat an apple on January 1, 2, and 8 in 2022.
Sample Input 2
2024-02-26 2024-03-02
Sample Output 2
1
Beware the leap years.
Sample Input 3
2022-01-01 9999-12-31
Sample Output 3
832544
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
2 つの文字列 S, T が与えられます。 S, T いずれかの部分列となっているような文字列の数を 998244353 で割った余りを求めてください。
ただし、文字列 A が文字列 B の部分列であるとは、A の長さが 1 以上であり、B から 0 個以上の文字を取り除くことで A と一致させられることをさします。例えば atcoder や ac
は atcoder の部分列ですが、atcoderr や ca は部分列ではありません。
制約
- 1 \leq \lvert S\rvert, \lvert T\rvert \leq 1000
- S, T は英小文字からなる。
入力
入力は以下の形式で標準入力から与えられる。
S T
出力
答えを出力せよ。
入力例 1
abc bca
出力例 1
10
S= abc の部分列は a, b, c, ab, ac, bc, abc の 7 つ、
T= bca の部分列は b, c, a, bc, ba, ca, bca の 7 つです。
よって、いずれかの部分列となっている文字列は
a, b, c, ab, ac, ba, bc, ca, abc, bca の 10 個です。
入力例 2
aa aaaaa
出力例 2
5
条件をみたす文字列は a, aa, aaa, aaaa, aaaaa の 5 つです。
入力例 3
xzyyzxxzyy yzxyzyxzyx
出力例 3
758
Score : 6 points
Problem Statement
You are given two strings S and T. Find the number of strings that are subsequences of at least one of S and T, modulo 998244353.
Here, a string A is said to be a subsequence of string B when the length of A is at least 1 and A can result from removing zero or more characters from B. For example, atcoder and ac are subsequences of atcoder, while atcoderr and ca are not.
Constraints
- 1 \leq \lvert S\rvert, \lvert T\rvert \leq 1000
- S and T consist of lowercase English letters.
Input
Input is given from Standard Input in the following format:
S T
Output
Print the answer.
Sample Input 1
abc bca
Sample Output 1
10
S= abc has seven subsequences: a, b, c, ab, ac, bc, abc, while
T= bca has seven subsequences: b, c, a, bc, ba, ca, bca.
Therefore, we have ten strings that are subsequences of at least one of them: a, b, c, ab, ac, ba, bc, ca, abc, bca.
Sample Input 2
aa aaaaa
Sample Output 2
5
The sought strings are a, aa, aaa, aaaa, aaaaa.
Sample Input 3
xzyyzxxzyy yzxyzyxzyx
Sample Output 3
758
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
英小文字からなる文字列 S, T が与えられます。あなたは S の文字を一つ選んで好きな英小文字に書き換えることを 0 回以上 K 回以下行うことができます。
S を書き換えたあと、S の部分列かつ T の部分列であるような文字列のうち、最長のものの長さは最大で何文字になりますか?
ただし、文字列 x が文字列 y の部分列であるとは、y から 0 個以上の文字を取り除き、残りの文字を元の順序で連結することで x が得られることをいいます。
制約
- 1 \leq |S|, |T| \leq 1000
- 1 \leq K \leq 10
- S, T は英小文字からなる。
入力
入力は以下の形式で標準入力から与えられる。
S T K
出力
答えを出力せよ。
入力例 1
strength slang 1
出力例 1
4
例えば、S の 3 文字目を l に書き換えることで、 slng が S の部分列かつ T の部分列となります。
長さ 5 以上の文字列が S の部分列かつ T の部分列として現れるようにすることはできないので、4 を出力します。
入力例 2
asdbvaklwebjkalhakslhgweqwbq obqweogkmawgjkoanboebeoqejkazxcnmvqse 10
出力例 2
19
Score : 6 points
Problem Statement
You are given strings S and T consisting of lowercase English letters. You can do the following operation between 0 and K times: choose one of the characters of S and replace it with any lowercase English letter.
What is the length of the longest possible string that is a subsequence of S after the replacements and also a subsequence of T?
Here, a string x is said to be a subsequence of a string y if x can result from removing zero or more characters from y and concatenating the remaining strings without changing the order.
Constraints
- 1 \leq |S|, |T| \leq 1000
- 1 \leq K \leq 10
- S and T consist of lowercase English letters.
Input
Input is given from Standard Input in the following format:
S T K
Output
Print the answer.
Sample Input 1
strength slang 1
Sample Output 1
4
By replacing the 3-rd character of S with l, slng becomes a subsequence of both S and T.
Since it is impossible to have a subsequence of both S and T of length 5 or longer, 4 should be printed.
Sample Input 2
asdbvaklwebjkalhakslhgweqwbq obqweogkmawgjkoanboebeoqejkazxcnmvqse 10
Sample Output 2
19
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
高橋くんと青木くんが、N 本先取でゲームの試合をします。高橋くんと青木くんの実力は全く同じであり、すべてのゲームは前後のゲームの結果等に左右されず、常に独立に高橋くんと青木くんが \frac{1}{2} ずつの確率で勝ちます。引き分けはありません。
(高橋くんの勝ち数, 青木くんの勝ち数) が (2,1) から (2,3) に動くことのように、2 ゲームが経過する間に 2 人の勝ち数の大小が入れ替わることを「逆転」と呼ぶことにします。
2 人の試合の決着がつくまでに起こる「逆転」の回数の期待値を\mod 998244353 で求めてください(注記参照)。
注記
求める期待値は必ず有理数となることが証明できます。またこの問題の制約下では、その値を互いに素な 2 つの整数 P, Q を用いて \frac{P}{Q} と表したとき、R \times Q \equiv P\pmod{998244353} かつ 0 \leq R \lt 998244353 を満たす整数 R がただ一つ存在することが証明できます。この R を求めてください。
制約
- 2 \leq N \leq 10^7
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
期待値を\mod 998244353 で出力せよ。
入力例 1
2
出力例 1
748683265
以下の 2 パターンのみ「逆転」が 1 回起きます。それ以外のパターンでは「逆転」は一度も起きません。
- 高橋くんが勝つ → 青木くんが勝つ → 青木くんが勝つ
- 青木くんが勝つ → 高橋くんが勝つ → 高橋くんが勝つ
これらのパターンは \frac{1}{8} ずつの確率で発生するため、期待値は \frac{1}{4} となります。
748683265 \times 4 \equiv 1\pmod{998244353} より、748683265 を出力してください。
入力例 2
4
出力例 2
405536769
入力例 3
621998
出力例 3
76706976
Score : 6 points
Problem Statement
Takahashi and Aoki will play a match where the first to win N games wins. The two players are equally skilled, and each of them wins a game with probability \frac{1}{2}, independently of the outcomes of the other games. There are no draws.
A reversal is said to occur when the player with more wins changes in two games, as in going from 2-1 to 2-3 (now Aoki is in the lead).
Find the expected value of the number of reversals until one player wins the match, modulo 998244353 (see Notes).
Notes
It can be proved that the sought expected value is a rational number. Additionally, under the Constraints of this problem, when that value is represented as \frac{P}{Q} using two coprime integers P and Q, it can be proved that there uniquely exists one integer R such that R \times Q \equiv P\pmod{998244353} and 0 \leq R \lt 998244353. Find this R.
Constraints
- 2 \leq N \leq 10^7
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
N
Output
Print the expected value modulo 998244353.
Sample Input 1
2
Sample Output 1
748683265
There is one reversal only in the two scenarios below, and no reversal in the other scenarios.
- Takahashi wins, then Aoki wins, then Aoki wins.
- Aoki wins, then Takahashi wins, then Takahashi wins.
Each of them occurs with probability \frac{1}{8}, so the sought expected value is \frac{1}{4}.
We have 748683265 \times 4 \equiv 1\pmod{998244353}, so print 748683265.
Sample Input 2
4
Sample Output 2
405536769
Sample Input 3
621998
Sample Output 3
76706976
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
縦横 H \times W マスのグリッドがあります。上から i 行目、左から j 列目のマスを (i,j) と表します。 各マスの状態は「何もないマス」か「壁があるマス」のいずれかです。はじめ、全てのマスは何もないマスです。
A さんは (1, 1) を出発してグリッド上を移動して (H, W) へ行こうとしています。A さんは (i,j) にいるときに (i+1,j),(i,j+1),(i-1,j),(i,j-1) のいずれかに移動することができます。ただし、グリッドの外に出るような移動や、壁があるマスへの移動を行うことはできません。
B さんは、A さんが移動を開始する前にいくつかのマスを選んで壁を建てることで、A さんがどのように移動しても (H, W) へ行くことができないようにすることにしました。
B さんが (i, j) に壁を建てるには c_{i, j} 円を払う必要があります。また、(1, 1), (H, W) には壁を建てられません。
B さんが条件を満たすように壁を建てるときに最小で何円払う必要があるでしょうか。また、その時の壁の立て方を出力してください。
制約
- 2 \leq H, W \leq 20
- 1 \leq c_{i,j} \leq 10^9 (1 \leq i \leq H, 1 \leq j \leq W, (i,j) \neq (1,1), (i,j) \neq (H,W))
- c_{1,1} = c_{H,W} = 0
- 入力はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。
H W
c_{1,1} c_{1,2} \dots c_{1,W}
c_{2,1} c_{2,2} \dots c_{2,W}
\vdots
c_{H,1} c_{H,2} \dots c_{H,W}
出力
H+1 行出力せよ。
1 行目には B さんが支払う最小の金額を出力せよ。
2 行目以降は以下の形式で出力せよ。ただし、G_{i,j} = . ならば (i,j) は壁を建てないマスで、G_{i,j}= # ならば (i,j) は壁を建てるマスとする。
G_{1,1}G_{1,2}\dotsG_{1,W}
G_{2,1}G_{2,2}\dotsG_{2,W}
\vdots
G_{H,1}G_{H,2}\dotsG_{H,W}
最小の金額で条件を満たす建て方が複数存在する場合はどれを出力してもよい。
入力例 1
2 3 0 6 4 2 3 0
出力例 1
7 ..# .#.
B さんが 7 円払って (1, 3) と (2, 2) に壁を建てるとA さんは (2, 3) へ行くことができなくなります。
これよりも少ない金額で条件を満たすように壁を建てることはできないので、これが答えとなります。
入力例 2
4 3 0 9 2 9 3 9 2 3 9 3 9 0
出力例 2
7 ..# .#. #.. ...
入力例 3
2 2 0 1000000000 1000000000 0
出力例 3
2000000000 .# #.
Score : 6 points
Problem Statement
There is a grid with H horizontal rows and W vertical columns. The square at the i-th row from the top and the j-th column from the left is called (i, j). The state of each square is either an "empty square" or a "square with a wall". Initially, every square is an empty square.
Ms. A wants to travel on the grid from (1, 1) to (H, W). When Ms. A is at (i, j), she may move to one of (i+1,j),(i,j+1),(i-1,j), and (i,j-1). She cannot go outside the grid or move to the square with a wall.
Ms. B has decided to choose some of the squares to build walls so that it is impossible for Ms. A to reach (H, W) no matter how she moves.
It costs Ms. B c_{i, j} yen (the currency in Japan) to build a wall on (i, j). She cannot build a wall on (1, 1) or (H, W).
What is the minimum cost Ms. B has to pay so that the condition is satisfied? Also, print the way of building walls to achieve the minimum cost.
Constraints
- 2 \leq H, W \leq 20
- 1 \leq c_{i,j} \leq 10^9 (1 \leq i \leq H, 1 \leq j \leq W, (i,j) \neq (1,1), (i,j) \neq (H,W))
- c_{1,1} = c_{H,W} = 0
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
H W
c_{1,1} c_{1,2} \dots c_{1,W}
c_{2,1} c_{2,2} \dots c_{2,W}
\vdots
c_{H,1} c_{H,2} \dots c_{H,W}
Output
Print H+1 lines.
The 1-st line should contain the minimum cost that Ms. B should pay.
The 2-nd and subsequent lines should be in the following format. Here, G_{i,j} = . means she will not build a wall on (i, j); G_{i,j}= # means she will build a wall on (i,j).
G_{1,1}G_{1,2}\dotsG_{1,W}
G_{2,1}G_{2,2}\dotsG_{2,W}
\vdots
G_{H,1}G_{H,2}\dotsG_{H,W}
If there are multiple ways to achieve the minimum cost, print any of them.
Sample Input 1
2 3 0 6 4 2 3 0
Sample Output 1
7 ..# .#.
If Ms. B pays 7 yen to build walls on (1, 3) and (2, 2), Ms. A will be unable to reach (2, 3).
Since it is impossible to satisfy the condition with less cost, this is the answer.
Sample Input 2
4 3 0 9 2 9 3 9 2 3 9 3 9 0
Sample Output 2
7 ..# .#. #.. ...
Sample Input 3
2 2 0 1000000000 1000000000 0
Sample Output 3
2000000000 .# #.
Time Limit: 8 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
xy 平面 P があります。
この平面に点を追加したり削除したりする操作を行うことを考えます。はじめ、 P にはひとつも点が追加されていません。
以下のクエリを、与えられた順に合計で Q 個処理してください。
+ x y
P 中の座標 (x,y) に点を 1 つ追加する。
- x y
P 中の座標 (x,y) にある点を 1 つ削除する。
各クエリを処理した直後に、以下の問いに答えてください。
現在 P に残っている任意の相異なる 2 点の(順序を問わない)組を考える。この 2 点の組は、 P 中に点が k 個残っている場合、 \frac{k(k-1)}{2} 通り考えられる。
このとき、それら全てに対して組を構成する 2 点と原点(座標 (0,0))からなる三角形の面積(ただし、この 3 点を全て通る直線が存在する場合、面積は 0 であるとする)の 2 倍を足し合わせた値(この値は整数になることが示せる)を 998244353 で割った余りを求める。
制約
- 1 \le Q \le 3 \times 10^5
+クエリは以下の制約を満たす。- -10^5 \le x,y \le 10^5 かつ (x,y) \neq (0,0)
-クエリの時点で、 (x,y) に点が 1 つ以上存在する。- 入力中の値はすべて整数である。
入力
入力は以下の形式で標準入力から与えられる。ただし、 \mathrm{Query}_i は i 個目のクエリを表す。
Q
\mathrm{Query}_1
\mathrm{Query}_2
\vdots
\mathrm{Query}_Q
出力
全体で Q 行出力せよ。
そのうち i 行目には、 i 個目のクエリを処理した直後の問いに対する答えを整数として出力せよ。
入力例 1
5 + 2 3 + -1 2 + 1 -2 - -1 2 + -1 -1
出力例 1
0 7 14 7 11
- 1 つ目のクエリで、 (2,3) に点を 1 つ追加します。
- このクエリを処理した時点で、問いに対する答えは 0 です。
- 2 つ目のクエリで、 (-1,2) に点を 1 つ追加します。
- (2,3),(-1,2),(0,0) からなる三角形の面積は \frac{7}{2} です。
- このクエリを処理した時点で、三角形の面積の総和は \frac{7}{2} なので、問いに対する答えは 7 です。
- 3 つ目のクエリで、 (1,-2) に点を 1 つ追加します。
- (2,3),(1,-2),(0,0) からなる三角形の面積は \frac{7}{2} です。
- (-1,2),(1,-2),(0,0) からなる三角形の面積は、この 3 点を全て通る直線が存在するので、 0 であるとします。
- このクエリを処理した時点で、三角形の面積の総和は 7 なので、問いに対する答えは 14 です。
- 4 つ目のクエリで、 (-1,2) にある点を 1 つ削除します。
- このクエリを処理した時点で、三角形の面積の総和は \frac{7}{2} なので、問いに対する答えは 7 です。
- 5 つ目のクエリで、 (-1,-1) に点を 1 つ追加します。
- (1,-2),(-1,-1),(0,0) からなる三角形の面積は \frac{3}{2} です。
- (-1,-1),(2,3),(0,0) からなる三角形の面積は \frac{1}{2} です。
- このクエリを処理した時点で、三角形の面積の総和は \frac{11}{2} なので、問いに対する答えは 11 です。
入力例 2
10 + 100000 100000 + 100000 -100000 + 100000 100000 + 100000 -100000 + 100000 100000 - 100000 100000 - 100000 -100000 - 100000 100000 - 100000 -100000 - 100000 100000
出力例 2
0 35112940 70225880 140451760 210677640 140451760 70225880 35112940 0 0
問いに対する答えを 998244353 で割った余りを求めることに注意してください。
同じ座標に複数個の点が追加される場合もあります。
点を削除する際、その座標に複数個の点があっても 1 つだけ削除することに注意してください。
入力例 3
10 + -5010 51358 + 95817 96893 + 19668 -58533 - 95817 96893 - -5010 51358 + 90155 -74912 - 90155 -74912 + -83888 -29953 - -83888 -29953 + 72565 37307
出力例 3
0 415181651 660233626 716858814 0 808940340 0 508110143 0 988223809
Score : 6 points
Problem Statement
There is a coordinate plane P.
Consider performing operations of plotting points in this plane and deleting them. Initially, no points are plotted in P.
Process a total of Q queries in the following forms in the given order.
+ x y
Plot a point at (x,y) in P.
- x y
Delete a point plotted at (x,y) in P.
After processing each query, answer the following question.
Consider all (unordered) pairs of points currently plotted in P; there are \frac{k(k-1)}{2} such pairs, where k is the current number of points plotted in P.
Find the sum of the following value (which is always an integer) over all those pairs modulo 998244353: the doubled area of the triangle whose vertices are the origin (the point (0,0)) and the points in the pair (if these three points lie on the same line, the area is assumed to be 0).
Constraints
- 1 \le Q \le 3 \times 10^5
- For each
+query, -10^5 \le x,y \le 10^5 and (x,y) \neq (0,0). - At each
-query, at least one point is plotted at (x,y). - All values in input are integers.
Input
Input is given from Standard Input in the following format, where \mathrm{Query}_i denotes the i-th query:
Q
\mathrm{Query}_1
\mathrm{Query}_2
\vdots
\mathrm{Query}_Q
Output
Print a total of Q lines, the i-th of which should contain the answer to the question when the i-th query has been processed as an integer.
Sample Input 1
5 + 2 3 + -1 2 + 1 -2 - -1 2 + -1 -1
Sample Output 1
0 7 14 7 11
- The 1-st query plots a point at (2,3).
- At this point, the answer to the question is 0.
- The 2-nd query plots a point at (-1,2).
- The area of the triangle with the vertices (2,3),(-1,2),(0,0) is \frac{7}{2}.
- At this point, the total area of the triangles is \frac{7}{2}, so the answer to the question is 7.
- The 3-rd query plots a point at (1,-2).
- The area of the triangle with the vertices (2,3),(1,-2),(0,0) is \frac{7}{2}.
- The area of the triangle with the vertices (-1,2),(1,-2),(0,0) is assumed to be 0 since these three points lie on the same line.
- At this point, the total area of the triangles is 7, so the answer to the question is 14.
- The 4-th query deletes a point at (-1,2).
- At this point, the total area of the triangles is \frac{7}{2}, so the answer to the question is 7.
- The 5-th query plots a point at (-1,-1).
- The area of the triangle with the vertices (1,-2),(-1,-1),(0,0) is \frac{3}{2}.
- The area of the triangle with the vertices (-1,-1),(2,3),(0,0) is \frac{1}{2}.
- At this point, the total area of the triangles is \frac{11}{2}, so the answer to the question is 11.
Sample Input 2
10 + 100000 100000 + 100000 -100000 + 100000 100000 + 100000 -100000 + 100000 100000 - 100000 100000 - 100000 -100000 - 100000 100000 - 100000 -100000 - 100000 100000
Sample Output 2
0 35112940 70225880 140451760 210677640 140451760 70225880 35112940 0 0
Be sure to find the sought sum modulo 998244353.
Also, multiple points may be plotted at the same coordinates.
Note that when deleting a point, just one point is deleted, not all of them at the specified coordinates.
Sample Input 3
10 + -5010 51358 + 95817 96893 + 19668 -58533 - 95817 96893 - -5010 51358 + 90155 -74912 - 90155 -74912 + -83888 -29953 - -83888 -29953 + 72565 37307
Sample Output 3
0 415181651 660233626 716858814 0 808940340 0 508110143 0 988223809