Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
あるバス停からは毎時 X 分にバスが出ます。 例えば、X=10 の場合、0 時 10 分、1 時 10 分、\dots、23 時 10 分にバスが出ます。 他の時刻にはバスは出ません。
いま、H 時 M 分 (M\neq X) です。次のバスは何分後に出ますか?
制約
- 0\leq H \leq 23
- 0\leq X,M \leq 59
- X\neq M
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
X H M
出力
答えを整数として出力せよ。
入力例 1
30 14 10
出力例 1
20
現在の時刻は 14 時 10 分であり、次にバスが出るのは 14 時 30 分なので、今から 20 分後です。
入力例 2
12 23 30
出力例 2
42
現在の時刻は 23 時 30 分であり、次にバスが出るのは翌日の 0 時 12 分なので、今から 42 分後です。
入力例 3
1 17 34
出力例 3
27
Problem Statement
There is a bus stop where buses depart at X minutes past each hour. For example, if X=10, buses depart at 0:10, 1:10, \ldots, and 23:10. No buses depart at any other time.
It is currently M minutes past H (M\neq X). How many minutes are left before the next bus departs?
Constraints
- 0\leq H \leq 23
- 0\leq X,M \leq 59
- X\neq M
- All input values are integers.
Input
The input is given from Standard Input in the following format:
X H M
Output
Print the answer as an integer.
Sample Input 1
30 14 10
Sample Output 1
20
It is 14:10 now. The next bus departs at 14:30, which is 20 minutes from now.
Sample Input 2
12 23 30
Sample Output 2
42
It is 23:30 now. The next bus departs at 0:12 on the next day, which is 42 minutes from now.
Sample Input 3
1 17 34
Sample Output 3
27
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
高橋君は銀行で N - 1 件の取引を行いました。
取引の内容は整数 A_1, A_2, \ldots, A_N によって表され、i 件目の取引は A_i < A_{i + 1} のとき A_{i + 1} - A_i 円の入金であり、A_i > A_{i + 1} のとき A_i - A_{i + 1} 円の出金です。ここで、与えられる入力は A_i \neq A_{i + 1} を満たします。
これらの取引における入金額の合計と出金額の合計をそれぞれ求めてください。
制約
- 2 \leq N \leq 100
- 0 \leq A_i \leq 10^7
- A_i \neq A_{i + 1}
- 入力される数値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N
出力
入金額の合計を X 円、出金額の合計を Y 円として、X と Y をこの順に空白区切りで出力せよ。
入力例 1
4 2 9 5 8
出力例 1
10 4
-
1 件目の取引は、2 < 9 であるため 9 - 2 = 7 円の入金です。
-
2 件目の取引は、9 > 5 であるため 9 - 5 = 4 円の出金です。
-
3 件目の取引は、5 < 8 であるため 8 - 5 = 3 円の入金です。
したがって、入金額の合計は 10 円、出金額の合計は 4 円となります。
入力例 2
5 10 8 6 4 2
出力例 2
0 8
Problem Statement
Takahashi made (N - 1) transactions at a bank.
The transactions are described by integers A_1, A_2, \ldots, A_N. The i-th transaction is a deposit of (A_{i + 1} - A_i) yen if A_i < A_{i + 1}, and a withdrawal of (A_i - A_{i + 1}) yen if A_i > A_{i + 1}. (Yen is a currency of Japan.) Here, it is guaranteed that the given input satisfies A_i \neq A_{i + 1}.
Find the total amounts of money deposited and withdrawn through these transactions.
Constraints
- 2 \leq N \leq 100
- 0 \leq A_i \leq 10^7
- A_i \neq A_{i + 1}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A_1 A_2 \ldots A_N
Output
If a total of X yen was deposited and Y yen was withdrawn through the transactions, print X and Y in this order, separated by a space.
Sample Input 1
4 2 9 5 8
Sample Output 1
10 4
- The 1-st transaction is a 9 - 2 = 7 yen deposit, as 2 < 9.
- The 2-st transaction is a 9 - 5 = 4 yen withdrawal, as 9 > 5.
- The 3-st transaction is a 8 - 5 = 3 yen deposit, as 5 < 8.
Thus, a total of 10 yen was deposited, and 4 yen was withdrawn.
Sample Input 2
5 10 8 6 4 2
Sample Output 2
0 8
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
良い数 を次のように定義します。
- 正整数 x が以下の条件を満たすとき、またその時に限って x を 良い数 と呼びます。
- x の隣接する桁の差は高々 1 である。
- 厳密には、 x が k 桁の整数であり、 x を十進表記で書き下すと d_1d_2 \dots d_k となる時、 1 \le i < k なる全ての整数 i について |d_i - d_{i+1}| \le 1 が満たされる。
例えば 1,56,777,3234 は良い数ですが、 13,1235,909 は良い数ではありません。
良さそうな数 を次のように定義します。
- 正整数 x が以下の条件を満たすとき、またその時に限って x を 良さそうな数 と呼びます。
- x の桁を高々 1 つ書き換えることで、 x を良い数にすることができる。 但し、この書き換えで先頭の桁を 0 にすることは許されない。
- 厳密には、 x が k 桁の整数であり、 x を十進表記で書き下すと d_1d_2 \dots d_k となる時、以下の条件を全て満たす整数組 (p,q) が存在する。
- 1 \le p \le k
- 0 \le q \le 9
- (p,q) \neq (1,0)
- x のうち d_p を q にすると、 x が良い数となる。
- 良い数は、必ず良さそうな数でもあることに注意してください。
例えば 7176 は d_2 を 8 にすることで 7876 とでき、 7876 は良い数なので 7176 は良さそうな数です。
整数 N が与えられるので、 N が良さそうな数かどうか判定してください。
制約
- N は 1 \le N < 10^{18} を満たす整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
N が良さそうな数なら Yes 、そうでないなら No と出力せよ。
入力例 1
7176
出力例 1
Yes
問題文中の例と同じです。
入力例 2
2020
出力例 2
No
2020 は良さそうな数ではありません。
入力例 3
3728
出力例 3
No
入力例 4
987654321012345678
出力例 4
Yes
N が 32bit 符号付き整数に収まらない場合もあります。
また、 N 自身が良い数である場合もあります。
Problem Statement
A good number is defined as follows.
- A positive integer x is said to be a good number if and only if:
- every pair of adjacent digits in x has a difference of 1 or less.
- Formally, if x has k digits and its decimal representation is d_1d_2 \dots d_k, then |d_i - d_{i+1}| \le 1 for all integers i with 1 \le i < k.
For example, 1,56,777, and 3234 are good numbers, but 13,1235, and 909 are not.
A goodish number is defined as follows.
- A positive integer x is said to be a goodish number if and only if:
- one can modify at most one digit of x to make it a good number. Here, it is disallowed to produce a leading zero.
- Formally, if x has k digit and its decimal representation is d_1d_2 \dots d_k, there exists an integer pair (p,q) such that:
- 1 \le p \le k,
- 0 \le q \le 9,
- (p,q) \neq (1,0), and
- setting d_p in x to q makes x a good number.
- Note that a good number is always a goodish number.
For example, given 7176, one can set d_2 to 8 to make it 7876, which is a good number, so 7176 is a goodish number.
Given an integer N, determine if N is a goodish number.
Constraints
- N is an integer such that 1 \le N < 10^{18}.
Input
The input is given from Standard Input in the following format:
N
Output
Print Yes if N is a goodish number, and No otherwise.
Sample Input 1
7176
Sample Output 1
Yes
This is the same as the example in the problem statement.
Sample Input 2
2020
Sample Output 2
No
2020 is not a goodish number.
Sample Input 3
3728
Sample Output 3
No
Sample Input 4
987654321012345678
Sample Output 4
Yes
N may not fit into a 32-bit signed integer.
Also, N itself may be a good number.
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
あるプログラミングコンテストに N チームが参加しました。
このコンテストの競技時間は T 分間でした。
チーム i の正解問題数は A_i 、最終正解時刻は B_i でした。
このコンテストでは、以下の規則で順位を決定します。
- より多くの問題を正解した方が上位となる。
- 正解問題数が同じチーム同士では、その中で最終正解時刻がより小さい方が上位となる。
- 正解問題数も最終正解時刻も同じチーム同士では、その中でチーム番号がより小さい方が上位となる。
1 位のチームの正解問題数を A' 、最終正解時刻を B' とします。
全てのチームについて、以下の値 G_i を求めてください。
- G_i = T \times (A' - A_i) + (B_i - B')
制約
- 入力は全て整数
- 1 \le N \le 1000
- 1 \le T \le 1000
- 1 \le A_i \le 1000
- 1 \le B_i \le T
入力
入力は以下の形式で標準入力から与えられる。
N T A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
全体で N 行出力せよ。
そのうち i 行目には、 G_i を整数として出力せよ。
入力例 1
6 120 3 80 4 90 5 120 5 100 3 110 4 70
出力例 1
220 110 20 0 250 90
このコンテストには 6 チームが参加し、競技時間は 120 分でした。
1 位になったのは、 5 問正解して最終正解時刻が 100 であるチーム 4 です。
よって、各 G_i は次の通りです。
- G_1 = 120 \times (5-3) + (80-100) = 220
- G_2 = 120 \times (5-4) + (90-100) = 110
- G_3 = 120 \times (5-5) + (120-100) = 20
- G_4 = 120 \times (5-5) + (100-100) = 0
- G_5 = 120 \times (5-3) + (110-100) = 250
- G_6 = 120 \times (5-4) + (70-100) = 90
Problem Statement
N teams competed in a programming contest.
The contest lasted T minutes.
Team i solved A_i problems, and the last acceptance time was B_i.
In this contest, the ranks are determined as follows:
- Those who solved more problems rank higher.
- Among those with the same number of solved problems, those with earlier last acceptance time rank higher.
- Among those with the same number of solved problems and last acceptance time, those with a smaller team number rank higher.
Let A' be the number of problems solved by the team ranked first, and B' be its last acceptance time.
Find the following value G_i for each team.
- G_i = T \times (A' - A_i) + (B_i - B')
Constraints
- All input values are integers.
- 1 \le N \le 1000
- 1 \le T \le 1000
- 1 \le A_i \le 1000
- 1 \le B_i \le T
Input
The input is given from Standard Input in the following format:
N T A_1 B_1 A_2 B_2 \vdots A_N B_N
Output
Print N lines.
The i-th line should contain G_i as an integer.
Sample Input 1
6 120 3 80 4 90 5 120 5 100 3 110 4 70
Sample Output 1
220 110 20 0 250 90
Six teams participated in this contest, and it lasted 120 minutes.
The first-ranked team is team 4, which solved five problems and the last acceptance time is 100.
Therefore, G_i is calculated as follows.
- G_1 = 120 \times (5-3) + (80-100) = 220
- G_2 = 120 \times (5-4) + (90-100) = 110
- G_3 = 120 \times (5-5) + (120-100) = 20
- G_4 = 120 \times (5-5) + (100-100) = 0
- G_5 = 120 \times (5-3) + (110-100) = 250
- G_6 = 120 \times (5-4) + (70-100) = 90
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
あなたは C 言語に似たコメントアウトの仕組みを実装してみることにしました。
英小文字、 / および * からなる長さ N の文字列 S が与えられます。
あなたは S に対して以下の一連の操作を行います。
- 整数値を取る変数 x を用意する。はじめ x は 1 で初期化されている。
- 次の条件を満たす n を探す。
- x \leq n \leq |S| - 1
- S の n 文字目は
/、S の n + 1 文字目は*
- 2.の条件を満たす n が存在しない場合は操作を終了する。そうでない場合は、条件を満たす n のうち最小のものを i とおく。
- 次の条件を満たす n を探す。
- i + 2 \leq n \leq |S| - 1
- S の n 文字目は
*、S の n + 1 文字目は/
- 4.の条件を満たす n が存在しない場合は操作を終了する。そうでない場合は、条件を満たす n のうち最小のものを j とおく。
- S の i 文字目から j + 1 文字目までを取り除き、残った文字列を順序を保って連結したものを新たな S とする。その後、x の値を i に更新して 2. に戻る。
操作を終了した時点での S を出力してください。
制約
- 1 \leq N \leq 10^6
- S は英小文字、
/および*からなる長さ N の文字列 - N は整数
入力
入力は以下の形式で標準入力から与えられる。
N S
出力
操作を終了した時点での S を出力せよ。
入力例 1
7 a/*b*/c
出力例 1
ac
以下の説明では S の n 文字目を S_n と表します。
操作の内容を説明すると次のようになります。
- はじめ、S =
a/*b*/c, x = 1 である。 - 2.の条件を満たす n を探す。n = 2 は x \leq n \leq |S|-1 かつ S_{n} =
/、S_{n+1} =*という条件を満たし、かつ条件を満たす n の最小値である。よって i = 2 とおく。 - 4.の条件を満たす n を探す。n = 5 は i + 2 \leq n \leq |S| - 1 かつ S_{n} =
*、 S_{n+1} =/という条件を満たし、かつ条件を満たす n の最小値である。よって j = 5 とおく。 - S の i = 2 文字目から j + 1 = 6 文字目までを取り除き、残った文字列を順序を保って連結したものを新たな S とする。S は
acになる。その後、x の値を 2 に更新して、手順 2. に戻る。 - 2.の条件を満たす n を探すと、そのような n は存在しないことがわかる。よって、操作を終了する。
操作を終了した時点での S は ac です。よってこれを出力します。
入力例 2
10 /*a*//*b*/
出力例 2
操作を終了した時点で S が空文字列になる場合もあります。
入力例 3
18 /*/a/*b*/c/*d*/e*/
出力例 3
ce*/
Problem Statement
You want to implement a C-like comment-out system.
You are given a length-N string S consisting of /, *, and lowercase English letters.
You are asked to perform the following procedure against S.
- Prepare a variable x that takes on an integer value. x is initialized with 1.
- Seek for an n such that:
- x \leq n \leq |S| - 1; and
- the n-th character of S is
/and the (n + 1)-th character of S is*.
- If no n satisfies the conditions in step 2, terminate the procedure. Otherwise, let i be the smallest such n.
- Seek for an n such that:
- i + 2 \leq n \leq |S| - 1; and
- the n-th character of S is
*and the (n + 1)-th character of S is/.
- If no n satisfies the conditions in step 4, terminate the procedure. Otherwise, let j be the smallest such n.
- Remove the i-th through (j + 1)-th characters of S, concatenate the remaining strings without changing the order, and set S to the resulting string. Set x to i, and go back to step 2.
Print S resulting from the procedure.
Constraints
- 1 \leq N \leq 10^6
- S is a length-N string consisting of
/,*, and lowercase English letters. - N is an integer.
Input
The input is given from Standard Input in the following format:
N S
Output
Print the S resulting from the procedure.
Sample Input 1
7 a/*b*/c
Sample Output 1
ac
In this description, we denote the n-th character of S by S_n.
The procedure proceeds as follows.
- Initially, S =
a/*b*/cand x = 1. - Seek for an n satisfying the conditions in step 2. n = 2 satisfies x \leq n \leq |S|-1, S_{n} =
/, and S_{n+1} =*, and is the minimum n that satisfies these conditions. Thus, let i = 2. - Seek for an n satisfying the conditions in step 4. n = 5 satisfies i + 2 \leq n \leq |S| - 1, S_{n} =
*, and S_{n+1} =/, and is the minimum n that satisfies these conditions. Thus, let j = 5. - Remove the i = 2-nd through j + 1 = 6-th characters of S, concatenate the remaining strings without changing the order, and set S to the resulting string. Now S is
ac. Set x to 2, and go back to step 2. - Seeking for an n satisfying the conditions in step 2, one finds that there is no such n. Thus, the procedure terminates here.
At the end of the procedure, S results in ac, which should be printed.
Sample Input 2
10 /*a*//*b*/
Sample Output 2
At the end of the procedure, S may result in an empty string.
Sample Input 3
18 /*/a/*b*/c/*d*/e*/
Sample Output 3
ce*/
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
あなたはドミノを並べています。
各 1 \leq i \leq N について「ドミノ S_i が倒れるとドミノ T_i が倒れる」という計 N 個の情報が与えられます。
与えられた情報から「ドミノ X を倒すとドミノ Y が倒れる」といえるか判定してください。
制約
- 1 \leq N \leq 2\times 10^5
- N は整数
- S_i,T_i,X,Y は英小文字のみからなる長さ 1 以上 100 以下の文字列
- X \neq Y
- 全ての i で S_i \neq T_i
- (S_i,T_i) は相異なる
入力
入力は以下の形式で標準入力から与えられる。
N X Y S_1 T_1 \vdots S_N T_N
出力
与えられた情報から「ドミノ X を倒すとドミノ Y が倒れる」といえるとき Yes、いえないとき No と出力せよ。
入力例 1
5 second fourth first second second third third fourth fourth fifth fifth sixth
出力例 1
Yes
2 番目の情報からドミノ second が倒れるとドミノ third が倒れること、3 番目の情報からドミノ third が倒れるとドミノ fourth が倒れることがことがわかります。
よってドミノ second を倒すとドミノ fourth が倒れるといえます。
入力例 2
5 fourth second first second second third third fourth fourth fifth fifth sixth
出力例 2
No
与えられた情報からはドミノ fourth を倒すとドミノ second が倒れるとはいえません。
入力例 3
6 e d a b b a a c c d d e e a
出力例 3
Yes
入力例 4
1 a b x y
出力例 4
No
Problem Statement
You are lining up dominoes.
N clues are given: for each 1 \leq i \leq N, if domino S_i falls, then domino T_i will also fall.
Determine if the given clues imply that if domino X falls, then domino Y will also fall.
Constraints
- 1 \leq N \leq 2\times 10^5
- N is an integer.
- Each of S_i,T_i,X, and Y is a string of length between 1 and 100, inclusive, consisting of lowercase English letters.
- X \neq Y
- S_i \neq T_i for all i.
- (S_i,T_i) are distinct.
Input
The input is given from Standard Input in the following format:
N X Y S_1 T_1 \vdots S_N T_N
Output
Print Yes if the given clues imply that if domino X falls, then domino Y will also fall; print No otherwise.
Sample Input 1
5 second fourth first second second third third fourth fourth fifth fifth sixth
Sample Output 1
Yes
The second clue states that if domino second falls, then domino third will also fall; and the third clue states that if domino third falls, then domino fourth will also fall.
Thus, we can infer that if domino second falls, then domino fourth will also fall.
Sample Input 2
5 fourth second first second second third third fourth fourth fifth fifth sixth
Sample Output 2
No
One cannot infer from the given clues that if domino fourth falls, then domino second will also fall.
Sample Input 3
6 e d a b b a a c c d d e e a
Sample Output 3
Yes
Sample Input 4
1 a b x y
Sample Output 4
No
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
N 行 N 列の行列 A が与えられます。 A の i 行 j 列の要素を A(i,j) と表記します。 A の要素のうちちょうど 1 つが 0 で、それ以外の N^2-1 個は 1 以上 N 以下の整数です。
A の要素として唯一存在する 0 を 1 以上 N 以下の整数で置き換える方法であって、置き換えた後の A が以下の条件を満たすようなものの数を求めてください。
- 全ての 1\leq i,j,k\leq N について、A(A(i,j),k)=A(i,A(j,k))
制約
- 1\leq N \leq 300
- 0\leq A(i,j)\leq N
- A(i,j)\ (1\leq i,j\leq N) の中に 0 であるものはちょうど 1 つ存在する
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A(1,1) A(1,2) \dots A(1,N) A(2,1) A(2,2) \dots A(2,N) \vdots A(N,1) A(N,2) \dots A(N,N)
出力
答えを整数として出力せよ。
入力例 1
3 1 2 3 2 0 1 3 1 2
出力例 1
1
A(2,2) が 0 なので、これを 1 以上 3 以下の整数で置き換えたそれぞれの場合について条件を満たすか考えます。
- A(2,2) を 1 で置き換えたとき:条件を満たしません。例えば、(i,j,k)=(2,2,3) のとき、A(A(i,j),k)=3 ですが A(i,A(j,k))=2 です。
- A(2,2) を 2 で置き換えたとき:条件を満たしません。例えば、(i,j,k)=(3,3,2) のとき、A(A(i,j),k)=2 ですが A(i,A(j,k))=3 です。
- A(2,2) を 3 で置き換えたとき:条件を満たします。全ての 1\leq i,j,k\leq N について、A(A(i,j),k)=A(i,A(j,k)) が成立します。
よって、答えは 1 です。
入力例 2
3 2 1 0 1 2 3 1 3 2
出力例 2
0
入力例 3
6 4 5 5 2 4 2 5 2 2 4 5 4 5 2 0 4 5 4 2 4 4 5 2 5 4 5 5 2 4 2 2 4 4 5 2 5
出力例 3
2
Problem Statement
You are given an N-by-N matrix A. The element in the i-th row and j-th column of A is denoted by A(i,j). Exactly one element of A is 0, and each of the other (N^2-1) elements is an integer between 1 and N.
How many ways are there to replace the only element 0 in A with an integer between 1 and N, inclusive, such that the resulting A satisfies the following condition?
- A(A(i,j),k)=A(i,A(j,k)) for all 1\leq i,j,k\leq N.
Constraints
- 1\leq N \leq 300
- 0\leq A(i,j)\leq N
- There is exactly one occurrence of 0 in A(i,j)\ (1\leq i,j\leq N).
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N A(1,1) A(1,2) \dots A(1,N) A(2,1) A(2,2) \dots A(2,N) \vdots A(N,1) A(N,2) \dots A(N,N)
Output
Print the answer as an integer.
Sample Input 1
3 1 2 3 2 0 1 3 1 2
Sample Output 1
1
Since A(2,2) is 0, we consider replacing it with each integer between 1 and 3.
- If A(2,2) becomes 1: it does not satisfy the condition. For (i,j,k)=(2,2,3), we have A(A(i,j),k)=3 but A(i,A(j,k))=2.
- If A(2,2) becomes 2: it does not satisfy the condition. For (i,j,k)=(3,3,2), we have A(A(i,j),k)=2 but A(i,A(j,k))=3.
- If A(2,2) becomes 3: it satisfies the condition. A(A(i,j),k)=A(i,A(j,k)) for all 1\leq i,j,k\leq N.
Thus, the answer is 1.
Sample Input 2
3 2 1 0 1 2 3 1 3 2
Sample Output 2
0
Sample Input 3
6 4 5 5 2 4 2 5 2 2 4 5 4 5 2 0 4 5 4 2 4 4 5 2 5 4 5 5 2 4 2 2 4 4 5 2 5
Sample Output 3
2
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
整数 S と N 個の整数 a_1,a_2,\dots,a_N が与えられます。
N 個の整数と +, \times を使って、値が S になる数式を作ることは出来ますか?
ただし、
- N 個の整数はちょうど 1 回ずつ使ってください。
- 整数の順番は自由に入れ替えてもよいです。
- 括弧を使ってはいけません。
- 整数同士を演算子を使用せずにつなげる行為 (例えば 1 と 2 から 12 を作る) は認められません。
制約
- 2 \leq N \leq 6
- 1 \leq S \leq 10^{18}
- 1 \leq a_i \leq 1000
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N S a_1 a_2 \dots a_N
出力
値が S になる数式を作れない場合は No を出力せよ。
作れる場合は以下の形式で出力せよ。ここで E は問題文の条件を満たす式とする。
Yes E
数式は間に空白を入れずに 1 行で出力せよ。また、+, \times を意味する記号はそれぞれ +, x とする。
例えば出力したい数式が 1 \times 2 + 3 \times 4 \times 5 である場合は以下のように出力する必要がある。
1x2+3x4x5
答えが複数ある場合は、どれも出力しても正解とみなされる。
入力例 1
3 11 1 2 5
出力例 1
Yes 1+2x5
1 + 2 \times 5 という式は問題文の条件を全て満たすので、これを出力すればよいです。
また、 2 \times 5 + 1 という式も問題文の条件を全て満たすので、これを出力しても正解とみなされます。
入力例 2
5 2 1 1 1 1 1
出力例 2
Yes 1+1x1x1x1
同じ整数が a_1, a_2, \dots, a_N に複数回登場する場合は、登場する回数の分だけ使用してください。
入力例 3
2 12 1 2
出力例 3
No
入力例 4
6 302934 614 490 585 613 420 945
出力例 4
Yes 420+490x613+585+614+945
Problem Statement
You are given an integer S, and N integers a_1,a_2,\dots,a_N.
Can you construct a mathematical expression that evaluates to S using +, \times, and the N integers?
Here,
- use each of the N integers exactly once.
- You can freely rearrange the integers.
- You may not use parentheses.
- You may not join integers without an operator in between (for example, join 1 and 2 to form 12).
Constraints
- 2 \leq N \leq 6
- 1 \leq S \leq 10^{18}
- 1 \leq a_i \leq 1000
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N S a_1 a_2 \dots a_N
Output
Print No if one cannot construct a mathematical expression that evaluates to S.
If it is possible, print one in the following format, where E is a sought expression.
Yes E
The expression must not contain a whitespace or a newline. The operators + and \times must be represented by + and x.
For example, if you want to print the expression 1 \times 2 + 3 \times 4 \times 5, it must be printed in the following format:
1x2+3x4x5
If there are multiple solutions, printing any of them is accepted.
Sample Input 1
3 11 1 2 5
Sample Output 1
Yes 1+2x5
The expression 1 + 2 \times 5 satisfies the conditions in the problem statement, so you may print this.
The expression 2 \times 5 + 1 also satisfies the conditions, so printing it is also accepted.
Sample Input 2
5 2 1 1 1 1 1
Sample Output 2
Yes 1+1x1x1x1
If the same integer occurs in a_1, a_2, \dots, a_N multiple times, use it as many times as it occurs.
Sample Input 3
2 12 1 2
Sample Output 3
No
Sample Input 4
6 302934 614 490 585 613 420 945
Sample Output 4
Yes 420+490x613+585+614+945
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
AtCoder 国には島 1, 島 2,\ldots, 島 N の N 個の島があります。 また、AtCoder 国には道 1, 道 2,\ldots, 道 M の M 本の道があり、道 i は島 A _ i と島 B _ i を双方向に結んでいます。 道 i\ (1\leq i\leq M) は D _ i 日に沈んでしまうため、D _ i 日以降に道 i を利用することはできません(D _ i 日にも利用できません)。
どの 2 つの島もいくつかの利用可能な道を使って行き来できることを、すべての島が連結であるということにします。 0 日には(つまり、どの道も沈んでいないときには)、すべての島は連結です。 X-1 日にはすべての島が連結であるが、X 日にはそうでないような整数 X を求めてください。
制約
- 2\leq N\leq2\times10 ^ 5
- N-1\leq M\leq2\times10 ^ 5
- 1\leq A _ i\leq B _ i\leq N\ (1\leq i\leq M)
- 1\leq D _ i\leq10 ^ 9\ (1\leq i\leq M)
- はじめ、すべての島は連結
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M A _ 1 B _ 1 D _ 1 A _ 2 B _ 2 D _ 2 \vdots A _ M B _ M D _ M
出力
答えを出力せよ。
入力例 1
5 6 1 2 10 1 3 25 2 3 35 2 4 15 3 4 30 4 5 40
出力例 1
25
AtCoder 国の島は以下の図のようになっています。
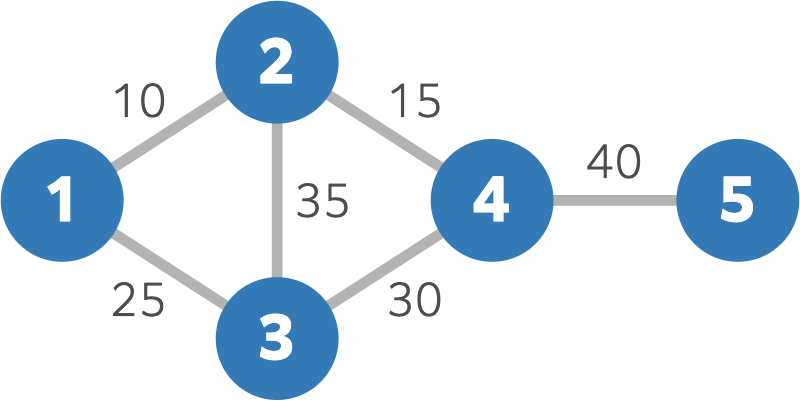
24 日には、すべての島が連結です。
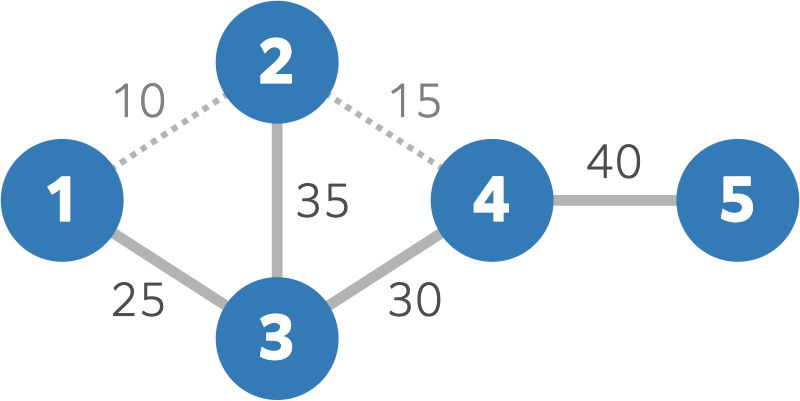
25 日には道 2 が沈み、たとえば島 1 と島 2 を行き来することができなくなります。
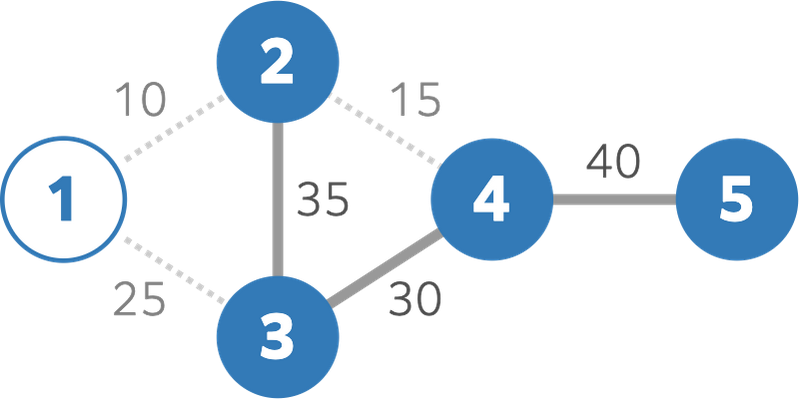
よって、25 を出力してください。
入力例 2
3 4 1 2 31 2 3 4 2 3 15 3 3 9
出力例 2
15
同じ島へ戻ってくる道や、全く同じ島どうしを結んでいる複数の道がある場合もあります。
入力例 3
15 20 6 7 54 5 15 63 8 14 30 5 8 52 5 9 96 1 13 51 8 13 89 4 15 81 12 12 80 4 10 48 1 11 63 1 9 72 10 14 83 3 5 30 7 12 60 1 10 60 2 11 68 5 7 52 6 12 34 1 8 41
出力例 3
30
Problem Statement
AtCoderLand has N islands: island 1, island 2, \ldots, and island N, and M roads: road 1, road 2, \ldots, and road M. Road i connects island A_i and island B_i bidirectionally. Road i\ (1\leq i\leq M) will be submerged on day D_i, so it will not be available on or after day D_i.
The islands are said to be connected if one can travel between any pair of islands via available roads. On day 0 (when no road is submerged), the islands are connected. Find the integer X such that the islands are connected on day (X-1) but not on day X.
Constraints
- 2\leq N\leq2\times10 ^ 5
- N-1\leq M\leq2\times10 ^ 5
- 1\leq A _ i\leq B _ i\leq N\ (1\leq i\leq M)
- 1\leq D _ i\leq10 ^ 9\ (1\leq i\leq M)
- The islands are initially connected.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M A _ 1 B _ 1 D _ 1 A _ 2 B _ 2 D _ 2 \vdots A _ M B _ M D _ M
Output
Print the answer.
Sample Input 1
5 6 1 2 10 1 3 25 2 3 35 2 4 15 3 4 30 4 5 40
Sample Output 1
25
The islands of AtCoderLand are illustrated in the figure below:

On day 24, the islands are connected.

On day 25, road 2 will be submerged, making it impossible to travel between, for instance, island 1 and island 2.

Thus, 25 should be printed.
Sample Input 2
3 4 1 2 31 2 3 4 2 3 15 3 3 9
Sample Output 2
15
There may be a road that leads from an island to itself, or multiple roads between the same pair of islands.
Sample Input 3
15 20 6 7 54 5 15 63 8 14 30 5 8 52 5 9 96 1 13 51 8 13 89 4 15 81 12 12 80 4 10 48 1 11 63 1 9 72 10 14 83 3 5 30 7 12 60 1 10 60 2 11 68 5 7 52 6 12 34 1 8 41
Sample Output 3
30
Time Limit: 3 sec / Memory Limit: 1024 MiB
問題文
1 から 3N までの番号がついた 3N 人の人がいます。人 i は A_i 円持っています。
3N 人を N 組の 3 人組に分けます。i 番目の組に含まれる人の所持金の金額の総和を S_i 円とします。
3N 人をうまく N 組に分けたとき、\displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k は最小でいくつになりますか?
制約
- 2 \leq N \leq 5
- 0 \leq A_i \leq 10^8
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
A_1 A_2 \dots A_{3N}
出力
\displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k が取りうる最小の値を出力せよ。
入力例 1
2 1 3 4 6 2 9
出力例 1
1
1 組目に人 1, 人 2, 人 6 を、2 組目に人 3, 人 4, 人 5 を割り当てると、
- S_1 = 1 + 3 + 9 = 13
- S_2 = 4 + 6 + 2 = 12
- \displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k = 13 - 12 = 1
になります。\displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k が 1 より小さくなる分け方は存在しないため、答えは 1 です。
入力例 2
2 0 0 0 0 0 100000000
出力例 2
100000000
入力例 3
5 614 490 420 945 613 585 760 38 926 725 667 685 449 455 873
出力例 3
35
Problem Statement
There are 3N people numbered from 1 to 3N. Person i has A_i yen (currency in Japan).
You are going to group the 3N people into N groups of three people each. Let S_i be the total amount of yen in the i-th group.
Find the minimum possible \displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k.
Constraints
- 2 \leq N \leq 5
- 0 \leq A_i \leq 10^8
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N
A_1 A_2 \dots A_{3N}
Output
Print the minimum possible \displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k.
Sample Input 1
2 1 3 4 6 2 9
Sample Output 1
1
If you group person 1, person 2, and person 6 into group 1, and person 3, person 4, and person 5 into group 2, then
- S_1 = 1 + 3 + 9 = 13,
- S_2 = 4 + 6 + 2 = 12,
- \displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k = 13 - 12 = 1.
No grouping makes \displaystyle \max_{1 \leq k \leq N} S_k - \min_{1 \leq k \leq N}S_k less than 1, so the answer is 1.
Sample Input 2
2 0 0 0 0 0 100000000
Sample Output 2
100000000
Sample Input 3
5 614 490 420 945 613 585 760 38 926 725 667 685 449 455 873
Sample Output 3
35
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
頂点に 1 から N の番号がついた N 頂点の木があります。 i 番目の辺は頂点 u_i と頂点 v_i を双方向に結んでいます。また、頂点 i には整数 A_i が書かれています。
N 個の頂点から K 個の頂点を選ぶ方法であって、どの選んだ頂点も隣接しないものが存在するか判定してください。存在する場合、選んだ K 個の頂点に書かれた整数の総和の最大値を求めてください。
制約
- 2\leq N\leq 100
- 1\leq K \leq N
- 1\leq u_i,v_i\leq N
- 1\leq A_i \leq 100
- 入力されるグラフは木
- 入力される数値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N K
u_1 v_1
\vdots
u_{N-1} v_{N-1}
A_1 \ldots A_N
出力
条件を満たす選び方が存在しない場合 -1 を出力せよ。条件を満たす選び方が存在する場合、選んだ K 個の頂点に書かれた整数の総和の最大値を出力せよ。
入力例 1
5 2 1 2 2 3 1 4 2 5 3 1 4 1 5
出力例 1
9
頂点 3 と頂点 5 を選ぶのが最適です。
入力例 2
10 6 7 3 3 8 5 1 3 9 2 5 6 1 5 4 10 7 7 1 1 3 10 6 7 9 2 2 10 4
出力例 2
34
入力例 3
10 6 2 10 1 10 7 4 8 9 8 7 4 3 1 4 6 7 5 3 2 5 1 2 3 6 2 9 9 7
出力例 3
-1
条件を満たす選び方は存在しません。
Problem Statement
There is an N-vertex tree whose vertices are numbered 1 through N. The i-th edge connects vertex u_i and vertex v_i bidirectionally. Vertex i has an integer A_i written on it.
Determine if there is a way to choose K vertices among the N so that no pair of chosen vertices are adjacent. If there is, find the maximum sum of integers written on the chosen K vertices.
Constraints
- 2\leq N\leq 100
- 1\leq K \leq N
- 1\leq u_i,v_i\leq N
- 1\leq A_i \leq 100
- The input graph is a tree.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N K
u_1 v_1
\vdots
u_{N-1} v_{N-1}
A_1 \ldots A_N
Output
Print -1 if there is no conforming choice. If there is, print the maximum sum of the integers written on chosen K vertices.
Sample Input 1
5 2 1 2 2 3 1 4 2 5 3 1 4 1 5
Sample Output 1
9
It is optimal to choose vertex 3 and vertex 5.
Sample Input 2
10 6 7 3 3 8 5 1 3 9 2 5 6 1 5 4 10 7 7 1 1 3 10 6 7 9 2 2 10 4
Sample Output 2
34
Sample Input 3
10 6 2 10 1 10 7 4 8 9 8 7 4 3 1 4 6 7 5 3 2 5 1 2 3 6 2 9 9 7
Sample Output 3
-1
There is no conforming choice.
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
以下の条件のいずれかを満たす長さ k の数列 A=(A_1,\ldots,A_k) をジグザグ列と呼びます。
-
A_1 < A_2> A_3 < A_4 > \ldots
-
A_1 > A_2 < A_3 > A_4 <\ldots
より厳密には、以下の条件を共に満たす数列をジグザグ列と呼びます。
- A_i \neq A_{i+1}\ (1\leq i \leq k-1)
- (A_{i+1}-A_i)(A_i-A_{i-1}) < 0\ (2\leq i \leq k-1)
特に、長さが 1 の列は常にジグザグ列であることに注意してください。
長さ N の数列 B=(B_1,\ldots,B_N) が与えられるので、B の部分列のうちジグザグ列であるものの長さの最大値を求めてください。
部分列とは
数列の部分列とは、数列から 0 個以上の要素を取り除いた後、残りの要素を元の順序で連結して得られる数列のことをいいます。 例えば、(10,30) は (10,20,30) の部分列ですが、(20,10) は (10,20,30) の部分列ではありません。制約
- 1\leq N \leq 2 \times 10^5
- 1\leq B_i\leq 10^9
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N B_1 \ldots B_N
出力
答えを一行に出力せよ。
入力例 1
7 5 1 2 3 4 3 3
出力例 1
4
B の部分列 (5,2,4,3) はジグザグ列であり、長さは 4 です。
入力例 2
5 1 2 3 4 5
出力例 2
2
Problem Statement
A length-k sequence A=(A_1,\ldots,A_k) is a zigzag sequence if:
-
A_1 < A_2> A_3 < A_4 > \ldots , or
-
A_1 > A_2 < A_3 > A_4 <\ldots .
More formally, a sequence is said to be a zigzag sequence if and only if:
- A_i \neq A_{i+1}\ (1\leq i \leq k-1), and
- (A_{i+1}-A_i)(A_i-A_{i-1}) < 0\ (2\leq i \leq k-1).
Especially, note that a sequence of length one is always a zigzag sequence.
Given a length-N sequence B=(B_1,\ldots,B_N), find the maximum length of a subsequence of B that is a zigzag sequence.
What is a subsequence?
A subsequence of a sequence is obtained by removing zero or more elements from the original sequence and concatenating the rest preserving the order. For example, (10,30) is a subsequence of (10,20,30), but (20,10) is not a subsequence of (10,20,30).Constraints
- 1\leq N \leq 2 \times 10^5
- 1\leq B_i\leq 10^9
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N B_1 \ldots B_N
Output
Print the answer in one line.
Sample Input 1
7 5 1 2 3 4 3 3
Sample Output 1
4
The subsequence (5,2,4,3) of B is a zigzag sequence of length 4.
Sample Input 2
5 1 2 3 4 5
Sample Output 2
2
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
N 頂点 M 辺の単純有向グラフが与えられます。 頂点には 1 から N までの番号が、辺には 1 から M までの番号がそれぞれ付けられており、辺 j は頂点 U_j から頂点 V_j に向かって伸びています。 各頂点には得点と呼ばれる整数値が定まっており、頂点 i の得点は P_i です。 また、各辺には減衰率と呼ばれる 0 以上 1 以下の実数値が定まっており、辺 j の減衰率は W_j です。 なお、与えられるグラフには有向閉路が存在しないことが保証されます(すなわち、ある頂点 i からいくつか辺を辿って再び頂点 i に戻ってくる方法は存在しません)。
高橋君はこのグラフ上でゲームをしようとしています。 最初、頂点 1 にコマが 1 つおいてあり、高橋君のスコアは 0 です。 高橋君は、今から以下のように操作を行うことで、コマを頂点 N まで動かしながらスコアを増やしていきます。
- 現在コマが置いてある頂点の番号を i とする。頂点 i の得点 P_i をスコアに加算する。
- i=N ならばゲームを成功として終了する。
- 頂点 i から伸びている辺が存在しないならば、ゲームを失敗として終了する。そうでないならば、頂点 i から伸びている辺を 1 本選ぶ。
- 選んだ辺の番号を j とする。各頂点の得点に辺 j の減衰率をかける。すなわち、各 i\ (1\leq i\leq N) に対して P_i \leftarrow P_i\times W_j とする。
- コマを頂点 V_j に動かし、1. に戻る。
高橋君がゲームを成功として終了させることが可能かどうか判定し、可能ならばゲーム終了時におけるスコアの最大値を求めてください。
制約
- N,M,P_i,U_j,V_j は整数
- 2\leq N \leq 10^5
- 1\leq M \leq 10^5
- 1\leq P_i\leq 10^4
- U_j \neq V_j
- (U_j,V_j)\neq (U_k, V_k)\ (j\neq k)
- 0\leq W_j\leq 1
- W_j は 10^{-6} の倍数であり、小数点以下第 6 位まで与えられる
- 与えられるグラフに有向閉路は存在しない
入力
入力は以下の形式で標準入力から与えられる。
N M P_1 P_2 \dots P_N U_1 V_1 W_1 U_2 V_2 W_2 \vdots U_M V_M W_M
出力
高橋君がゲームを成功として終了させることが可能ならばゲーム終了時におけるスコアの最大値を、不可能ならば -1 を出力せよ。
なお、前者の場合、真の値との絶対誤差または相対誤差が 10^{−6} 以下であれば正解として扱われる。
入力例 1
4 4 2 5 3 1 1 3 0.500000 1 2 0.250000 2 3 0.250000 3 4 0.500000
出力例 1
3.7500000000
以下、数列 (P_1,P_2,P_3,P_4) のことを簡単に P と表記します。 最初、P=(2,5,3,1) です。
コマを頂点 1\rightarrow 3\rightarrow 4 と動かすとき、ゲームは以下のように進行します。
- 頂点 1 の得点 P_1=2 をスコアに加算する。
- 頂点 1 から伸びている辺のうち辺 1 を選ぶ。
- 各頂点の得点に辺 1 の減衰率 W_1=0.5 をかける。P=(1,2.5,1.5,0.5) になる。
- コマを頂点 V_1=3 に動かす。
- 頂点 3 の得点 P_3=1.5 をスコアに加算する。
- 頂点 3 から伸びている辺のうち辺 4 を選ぶ。
- 各頂点の得点に辺 4 の減衰率 W_4=0.5 をかける。P=(0.5,1.25,0.75,0.25) になる。
- コマを頂点 V_4=4 に動かす。
- 頂点 4 の得点 P_4=0.25 をスコアに加算する。
- ゲームを成功として終了する。
このとき、ゲーム終了時におけるスコアは 2+1.5+0.25=3.75 となり、これが最大値です。
入力例 2
3 1 1 1 1 1 2 0.000000
出力例 2
-1
ゲームを成功として終了させることはできません。
入力例 3
6 12 22 75 26 45 72 81 4 6 0.185514 3 6 0.758252 2 3 0.622989 2 4 0.984614 1 3 0.465086 1 5 0.396959 5 3 0.618272 5 2 0.016128 1 2 0.869673 1 4 0.363219 2 6 0.097935 5 4 0.877468
出力例 3
138.6258141601
Problem Statement
You are given an N-vertex M-edge simple directed graph. The vertices are numbered 1 through N, and the edges are numbered 1 through M. Edge j directs from vertex U_j to vertex V_j. Each vertex has an integer attribute point: the point of vertex i is P_i. Also, each edge has a real attribute decay between 0 and 1: the decay of edge j is W_j. It is guaranteed that the given graph does not have a closed cycle. (In other words, there is no way to travel from a vertex i along edges to go back to vertex i.)
Takahashi is going to play a game on this graph. Initially, vertex 1 has a piece on it, and Takahashi's score is 0. He performs the following procedure to move the piece to vertex N while accumulating his score.
- Let i be the current number of vertex with the piece. Add the point P_i of vertex i to his score.
- If i=N, he ends the game successfully.
- If there is no edge going from vertex i, he ends the game unsuccessfully. Otherwise, choose an edge going from vertex i.
- Let j be the number of the chosen edge. Multiply the point of each vertex by the decay of edge j. In other words, let P_i \leftarrow P_i\times W_j for each i\ (1\leq i\leq N).
- Move the piece to vertex V_j, and jump to step 1.
Determine if he can end the game successfully. If it is possible, print the maximum possible final score of the game.
Constraints
- N,M,P_i,U_j, and V_j are integers.
- 2\leq N \leq 10^5
- 1\leq M \leq 10^5
- 1\leq P_i\leq 10^4
- U_j \neq V_j
- (U_j,V_j)\neq (U_k, V_k)\ (j\neq k)
- 0\leq W_j\leq 1
- W_j is a multiple of 10^{-6} and given with six decimal places.
- The given graph does not have a directed cycle.
Input
The input is given from Standard Input in the following format:
N M P_1 P_2 \dots P_N U_1 V_1 W_1 U_2 V_2 W_2 \vdots U_M V_M W_M
Output
Print the maximum possible final score if he can successfully end the game, and -1 otherwise.
In the former case, your answer is considered correct if the absolute or relative error from the true value is at most 10^{−6}.
Sample Input 1
4 4 2 5 3 1 1 3 0.500000 1 2 0.250000 2 3 0.250000 3 4 0.500000
Sample Output 1
3.7500000000
We denote the sequence (P_1,P_2,P_3,P_4) simply by P. Initially, P=(2,5,3,1).
If he moves the piece along vertices 1\rightarrow 3\rightarrow 4, the game proceeds as follows.
- Add the point P_1=2 of vertex 1 to his score.
- Among the edges going from vertex 1, choose edge 1.
- Multiply the point of each vertex by the decay W_1=0.5 of edge 1. Now, P=(1,2.5,1.5,0.5).
- Move the piece to vertex V_1=3.
- Add the point P_3=1.5 of vertex 3 to his score.
- Among the edges going from vertex 3, choose edge 4.
- Multiply the point of each vertex by the decay W_4=0.5 of edge 4. Now, P=(0.5,1.25,0.75,0.25).
- Move the piece to vertex V_4=4.
- Add the point P_4=0.25 of vertex 4 to his score.
- He ends the game successfully.
In this case, the final score is 2+1.5+0.25=3.75, which is maximum possible.
Sample Input 2
3 1 1 1 1 1 2 0.000000
Sample Output 2
-1
He cannot end the game successfully.
Sample Input 3
6 12 22 75 26 45 72 81 4 6 0.185514 3 6 0.758252 2 3 0.622989 2 4 0.984614 1 3 0.465086 1 5 0.396959 5 3 0.618272 5 2 0.016128 1 2 0.869673 1 4 0.363219 2 6 0.097935 5 4 0.877468
Sample Output 3
138.6258141601
Time Limit: 2 sec / Memory Limit: 1024 MiB
問題文
長さ N の非負整数列 A=(A _ 1,A _ 2,\ldots,A _ N) と 0 より大きく 1 以下の実数 x が与えられます。
整数の組 (l,r)\ (1\leq l\leq r\leq N) に対して、f(l,r) を以下のように定めます。
Q 個の質問に答えてください。 i 個目の質問 (1\leq i\leq Q) では整数の組 (l _ i,r _ i)\ (1\leq l _ i\leq r _ i\leq N) が与えられるので、f(l _ i,r _ i) の値を求めてください。
制約
- 1\leq N\leq2\times10 ^ 5
- 0\leq A _ i\leq10 ^ 9\ (1\leq i\leq N)
- 0\lt x\leq 1
- 1\leq Q\leq2\times10 ^ 5
- 1\leq l _ i\leq r _ i\leq N\ (1\leq i\leq Q)
- N,A _ i,Q,l _ i,r _ i は整数
- x は小数点以下たかだか 15 桁の実数として与えられる
入力
入力は以下の形式で標準入力から与えられる。
N A _ 1 A _ 2 \ldots A _ N x Q l _ 1 r _ 1 l _ 2 r _ 2 \vdots l _ Q r _ Q
出力
Q 行出力せよ。 i 行目 (1\leq i\leq Q) には i 個目の質問 (l _ i,r _ i) に対する f(l _ i,r _ i) の値を出力せよ。 真の値との相対誤差もしくは絶対誤差が 10 ^ {-6} 以下であれば正解と判定される。
入力例 1
7 3 1 4 1 5 9 2 0.25 4 1 3 3 6 1 7 2 2
出力例 1
3.5 4.703125 3.54443359375 1
各質問について、答えはそれぞれ以下のようになります。
- f(1,3)=A _ 1\times0.25 ^ 0+A _ 2\times0.25 ^ 1+A _ 3\times0.25 ^ 2=3+0.25+0.25=3.5 です。
- f(3,6)=A _ 3\times0.25 ^ 0+A _ 4\times0.25 ^ 1+A _ 5\times0.25 ^ 2+A _ 6\times0.25 ^ 3=4+0.25+0.3125+0.140625=4.703125 です。
- f(1,7)=A _ 1\times0.25 ^ 0+A _ 2\times0.25 ^ 1+A _ 3\times0.25 ^ 2+A _ 4\times0.25 ^ 3+A _ 5\times0.25 ^ 4+A _ 6\times0.25 ^ 5+A _ 7\times0.25 ^ 6=3+0.25+0.25+0.015625+0.01953125+0.0087890625+0.00048828125=3.54443359375 です。
- f(2,2)=A _ 2\times0.25 ^ 0=1 です。
相対誤差もしくは絶対誤差が 10 ^ {-6} 以下であれば正解になるので、
3.5 4.703125 3.54443359375 0.999999
や
3.4999965 4.703129703125 3.54443004931640625 1.000001
のように出力しても正解になります。
入力例 2
15 6 45 81 83 28 40 31 30 51 31 59 50 94 36 0 0.998244353 20 1 2 1 5 1 10 2 5 2 10 3 3 3 8 3 12 4 4 4 14 5 5 5 11 5 13 5 14 6 7 7 7 8 10 10 13 10 14 12 14
出力例 2
50.920995885 242.004326432639783195178618854259 422.764240065920208662445303267128 236.419395434977014285377699356 417.497217803865912440022892137641 81 292.066191815728552247199317241863 480.544234637661958884554506013369 83 528.144974561396676686531955107577 28 268.416129630805326045766513470066 410.492717775411750526215653552396 445.927866482402907904585917660160 70.945574943 31 111.801707440188046879 233.226782486727123857410847838 268.974634315843968519190799533618 179.708673560669989924
Problem Statement
You are given a length-N sequence A=(A _ 1,A _ 2,\ldots,A _ N) of non-negative integers, and a real value x strictly greater than 0 and less than or equal to 1.
For an integer pair (l,r)\ (1\leq l\leq r\leq N), we define f(l,r) as follows:
Answer Q queries. In the i-th query (1\leq i\leq Q), given an integer pair (l _ i,r _ i)\ (1\leq l _ i\leq r _ i\leq N), find f(l _ i,r _ i).
Constraints
- 1\leq N\leq2\times10 ^ 5
- 0\leq A _ i\leq10 ^ 9\ (1\leq i\leq N)
- 0\lt x\leq 1
- 1\leq Q\leq2\times10 ^ 5
- 1\leq l _ i\leq r _ i\leq N\ (1\leq i\leq Q)
- N,A _ i,Q,l _ i, and r _ i are integers.
- x is a real value with at most 15 decimal places.
Input
The input is given from Standard Input in the following format:
N A _ 1 A _ 2 \ldots A _ N x Q l _ 1 r _ 1 l _ 2 r _ 2 \vdots l _ Q r _ Q
Output
Print Q lines. The i-th line (1\leq i\leq Q) should contain the value f(l _ i,r _ i) for the i-th query (l _ i,r _ i). Your answer is considered correct if the relative or absolute error from the true value is at most 10 ^ {-6}.
Sample Input 1
7 3 1 4 1 5 9 2 0.25 4 1 3 3 6 1 7 2 2
Sample Output 1
3.5 4.703125 3.54443359375 1
For each query, the answer is as follows.
- f(1,3)=A _ 1\times0.25 ^ 0+A _ 2\times0.25 ^ 1+A _ 3\times0.25 ^ 2=3+0.25+0.25=3.5.
- f(3,6)=A _ 3\times0.25 ^ 0+A _ 4\times0.25 ^ 1+A _ 5\times0.25 ^ 2+A _ 6\times0.25 ^ 3=4+0.25+0.3125+0.140625=4.703125.
- f(1,7)=A _ 1\times0.25 ^ 0+A _ 2\times0.25 ^ 1+A _ 3\times0.25 ^ 2+A _ 4\times0.25 ^ 3+A _ 5\times0.25 ^ 4+A _ 6\times0.25 ^ 5+A _ 7\times0.25 ^ 6=3+0.25+0.25+0.015625+0.01953125+0.0087890625+0.00048828125=3.54443359375.
- f(2,2)=A _ 2\times0.25 ^ 0=1.
Since your answer is considered correct if the relative or absolute error is at most 10 ^ {-6}, output like
3.5 4.703125 3.54443359375 0.999999
and
3.4999965 4.703129703125 3.54443004931640625 1.000001
are also accepted.
Sample Input 2
15 6 45 81 83 28 40 31 30 51 31 59 50 94 36 0 0.998244353 20 1 2 1 5 1 10 2 5 2 10 3 3 3 8 3 12 4 4 4 14 5 5 5 11 5 13 5 14 6 7 7 7 8 10 10 13 10 14 12 14
Sample Output 2
50.920995885 242.004326432639783195178618854259 422.764240065920208662445303267128 236.419395434977014285377699356 417.497217803865912440022892137641 81 292.066191815728552247199317241863 480.544234637661958884554506013369 83 528.144974561396676686531955107577 28 268.416129630805326045766513470066 410.492717775411750526215653552396 445.927866482402907904585917660160 70.945574943 31 111.801707440188046879 233.226782486727123857410847838 268.974634315843968519190799533618 179.708673560669989924
Time Limit: 4 sec / Memory Limit: 1024 MiB
配点 : 6 点
問題文
4\times 4 のマス目について、次をみたす状態を 良い盤面 と定義します。
1 以上 15 以下の整数 i について i が書き込まれたマスがちょうど 1 つ存在する。
それら以外に何かが書かれたマスは存在せず、すなわち何も書かれていないマスがただ 1 つ存在する。
相異なる良い盤面 S, T が与えられます。
ここで、良い盤面 S は 16 個の整数 S_{i,j} (1\leq i,j\leq 4) によって与えられます。
1\leq S_{i,j}\leq 15 のとき、S の上から i 行目かつ左から j 列目のマスには S_{i,j} が書き込まれていることを、
S_{i,j}=-1 のとき、S の上から i 行目かつ左から j 列目のマスには何も書き込まれていないことを表します。
T も同様に 16 個の整数 T_{i,j} (1\leq i,j\leq 4) によって与えられます。
S から次の操作を繰り返して T の状態を作るために必要な最小の操作回数を出力してください。
ただし、30 回以下の操作で T の状態を作る事ができないとき(何回繰り返しても作る事ができない場合を含む)は -1 を出力してください。
- 何も書き込まれていないマスと辺を共有するマスを 1 つ選び、そのマスに書き込まれている整数を何も書き込まれていないマスに書き込む。その後、選んだマスに書かれている整数を消す。
制約
- -1\leq S_{i,j},T_{i,j}\leq 15
- S_{i,j},T_{i,j}\neq 0
- S,T は相異なる良い盤面である。
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
S_{1,1} S_{1,2} S_{1,3} S_{1,4}
S_{2,1} S_{2,2} S_{2,3} S_{2,4}
S_{3,1} S_{3,2} S_{3,3} S_{3,4}
S_{4,1} S_{4,2} S_{4,3} S_{4,4}
T_{1,1} T_{1,2} T_{1,3} T_{1,4}
T_{2,1} T_{2,2} T_{2,3} T_{2,4}
T_{3,1} T_{3,2} T_{3,3} T_{3,4}
T_{4,1} T_{4,2} T_{4,3} T_{4,4}
出力
S から問題文中の操作を繰り返して T の状態を作るために必要な操作回数を出力せよ。
ただし、30 回以下の操作で T の状態を作る事ができないときは -1 を出力せよ。
入力例 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -1 1 2 3 4 5 6 -1 8 9 10 7 11 13 14 15 12
出力例 1
3
マス目の上から i 行目かつ j 列目のマスを (i,j) で表すことにします。
S における何も書かれていないマスは (4,4) です。
ここから次のようにして 3 回の操作で T を作る事ができます。
- (3,4) を選ぶ。(4,4) に 12 を書き込み、(3,4) に書かれている整数を消す。
- (3,3) を選ぶ。(3,4) に 11 を書き込み、(3,3) に書かれている整数を消す。
- (2,3) を選ぶ。(3,3) に 7 を書き込み、(2,3) に書かれている整数を消す。
一方で、2 回以下の操作で T を作ることはできないため、3 を出力します。

入力例 2
-1 11 10 9 1 12 15 8 2 13 14 7 3 4 5 6 6 5 4 3 7 12 15 2 8 13 14 1 9 10 11 -1
出力例 2
-1
30 回以下の操作で T を作る事ができないため、-1 を出力します。
入力例 3
1 12 11 10 2 13 -1 9 3 14 15 8 4 5 6 7 1 10 5 14 2 11 6 15 3 12 7 -1 4 13 8 9
出力例 3
30
Score : 6 points
Problem Statement
A 4\times 4 grid is said to be good if it is in the following state:
For every integer i between 1 and 15, inclusive, there is exactly one cell with that integer written on it.
No other cell has something written on it. In other words, there is exactly one cell with nothing written on it.
You are given two distinct good grids S and T.
Here, the good grid S is given by 16 integers S_{i,j} (1\leq i,j\leq 4).
If 1\leq S_{i,j}\leq 15, it means that the cell in the i-th row from the top and j-th column from the left has S_{i,j} written on it;
if S_{i,j}=-1, it means that the cell in the i-th row from the top and j-th column from the left has nothing written on it.
Likewise, T is given by 16 integers T_{i,j} (1\leq i,j\leq 4).
Find the minimum number of times of performing the following operation to make the grid equal to T, starting from S.
If the grid cannot be made equal to T with 30 operations or less (including the case where any number of operations can do so), print -1 instead.
- Choose a cell adjacent to the cell with nothing written on it, and write the integer written on the chosen cell to the empty cell. Then, erase the integer written on the chosen cell.
Constraints
- -1\leq S_{i,j},T_{i,j}\leq 15
- S_{i,j},T_{i,j}\neq 0
- S and T are distinct good grids.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
S_{1,1} S_{1,2} S_{1,3} S_{1,4}
S_{2,1} S_{2,2} S_{2,3} S_{2,4}
S_{3,1} S_{3,2} S_{3,3} S_{3,4}
S_{4,1} S_{4,2} S_{4,3} S_{4,4}
T_{1,1} T_{1,2} T_{1,3} T_{1,4}
T_{2,1} T_{2,2} T_{2,3} T_{2,4}
T_{3,1} T_{3,2} T_{3,3} T_{3,4}
T_{4,1} T_{4,2} T_{4,3} T_{4,4}
Output
Print the minimum number of times of performing the operation in the problem statement to make the grid equal to T, starting from S.
If the grid cannot be make equal to T with 30 operations or less, print -1 instead.
Sample Input 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -1 1 2 3 4 5 6 -1 8 9 10 7 11 13 14 15 12
Sample Output 1
3
We denote by (i,j) the cell in the i-th row from the top and j-th column from the left in the grid.
In S, the empty cell is (4,4).
One can perform three operations to obtain T.
- Choose (3,4). Write 12 to (4,4), and erase the integer written on (3,4).
- Choose (3,3). Write 11 to (3,4), and erase the integer written on (3,3).
- Choose (2,3). Write 7 to (3,3), and erase the integer written on (2,3).
On the other hand, one cannot obtain T with two operations or less, so print 3.

Sample Input 2
-1 11 10 9 1 12 15 8 2 13 14 7 3 4 5 6 6 5 4 3 7 12 15 2 8 13 14 1 9 10 11 -1
Sample Output 2
-1
One cannot obtain T with 30 operations or less, so print -1.
Sample Input 3
1 12 11 10 2 13 -1 9 3 14 15 8 4 5 6 7 1 10 5 14 2 11 6 15 3 12 7 -1 4 13 8 9
Sample Output 3
30