問題文

5 以上の整数 N と長さ N の整数列 A=(A_1,A_2,\ldots,A_N) が与えられます。

A を降順に並べ替えた列を B=(B_1 ,B_2,\ldots,B_N)としたとき、B_4-B_5 を求めてください。

制約

• 5 \leq N \leq 30
• 0 \leq A_i \leq 1200 (1 \leq i \leq N)
• 入力は全て整数

入力例 1

6
768 587 622 0 674 601

出力例 1

14

入力例 2

6
614 670 451 549 553 540

出力例 2

9

入力例 3

10
1200 64 750 1200 800 900 900 100 314 999

出力例 3

0

問題文

アリの生息地として知られるパケンパークには、N 個のアリの巣と N-1 個の溝があります。巣には 1, 2 \ldots N 、溝には 1, 2 \ldots N-1 とそれぞれ順に番号がふられています。 i (1 \leq i \leq N-1)番の溝は巣 U_i と巣 V_i を双方向に結んでいます。ここで、任意の 2 つの巣は、いくつかの溝を経由して双方向に結ばれています。

生物学者であるパケン氏は、パケンパークに生息するアリに次のような習性があることを解明しました。

• 巣 s (1 \leq s \leq N) に生息するアリは、巣 s と直接溝で結ばれた巣の K 個以上にビスケットが存在する場合、またその場合に限りそれらの巣からビスケットを運び入れる。運び入れたのち、巣 s にはビスケットが存在するものとみなす。なお、この行動によって運び入れた元の巣からビスケットがなくなることはない。

パケン氏は実験としていくつかの巣を選び、それらの巣にビスケットを投入し、最終的にビスケットが存在する巣の個数を調査することにしました。N 個の巣から、最初にビスケットを投入する巣として 1 つ以上の巣を選ぶ方法は全部で 2^N-1 通りありますが、それぞれについて最終的にビスケットが存在する巣の個数を求め、その総和を P で割った余りを求めてください。

制約

• 1 \leq K \leq N \leq 10^6
• 10^8 \leq P \leq 10^9
• P は素数
• 1 \leq U_i \lt V_i \leq N (1 \leq i \leq N-1)
• 与えられるグラフは木である
• 入力は全て整数

小課題

1. (1 点) K = 1
2. (1 点) K = N-1
3. (2 点) N \leq 15
4. (6 点) U_i = i , V_i = i+1 (1 \leq i \leq N-1)
5. (35 点) N \leq 2000, K \leq 5
6. (15 点) K \leq 5
7. (25 点) N \leq 10^5
8. (15 点) 追加の制約はない

入力例 1

4 2 998244353
1 2
2 3
3 4

出力例 1

36

例えば、最初に巣 1, 3 にビスケットを投入したとします。すると、巣 2 のアリは巣 1, 3 の 2 (\geq K) 個の巣からビスケットを運び出します。最終的には 1,2,3 の 3 個の巣にビスケットが存在することになります。

このサンプルは小課題 3, 4, 5, 6, 7 の制約を満たします。

入力例 2

5 2 998244353
1 2
2 3
2 4
1 5

出力例 2

93

このサンプルは小課題 3, 5, 6, 7 の制約を満たします。

入力例 3

5 1 998244353
1 2
2 3
2 4
1 5

出力例 3

155

このサンプルは小課題 1, 3, 5, 6, 7 の制約を満たします。

入力例 4

5 4 998244353
1 2
1 3
1 4
1 5

出力例 4

81

このサンプルは小課題 2, 3, 5, 6, 7 の制約を満たします。

入力例 5

15 2 998244353
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
5 10
5 11
6 12
6 13
7 14
7 15

出力例 5

312049

このサンプルは小課題 3, 5, 6, 7 の制約を満たします。

問題文

パ研王国は N 個の町からなり、それぞれの町には 1, 2, \ldots, N の番号が付いています。これらの町は N-1 個の道路で結ばれており、道路には 1, 2, \ldots, N-1 の番号が付いています。道路 i (1 \leq i \leq N-1) は町 A_i と町 B_i を双方向に結んでいます。どの町からどの町へも 0 本以上の道路を通り移動できます。

2 つの町 a, b の距離を、 a から b に移動するときに通る辺の個数の最小値とします。特に、 a=b のとき、距離は 0 であることに注意してください。

パ研王国のそれぞれの町には、文字を売る店があります。パ研王国の文字は 1 以上 N 以下の整数で表され、町 i にある店では文字 C_i のみを買うことができます。それぞれの店には十分な在庫があり、売り切れることはないものとします。

さて、パ研王国ではこれから M 日間に渡りパレードが開催されます。 i 日目には、町 U_i から町 V_i へ移動する最短経路上にある町(町 U_i, V_i を含む)がパレードの開催される町となります。特に、 U_i = V_i のとき、パレードは町 U_i でのみ開催されます。パレードの開催される町の店は営業しており、文字を買うことができますが、それ以外の町にある店は全て閉じてしまい、文字を買うことができません。

パ研王国の王様であるあなたは、パレードを見に来た人たちに歓迎の意を伝えるため、 M 日間にわたり国民に指示を出します。 i 日目には、町 L_i, L_i+1, \ldots, R_i に住む住民それぞれ 1 人に対し、次のような指示を出します。

• i 日目にパレードの開催される町のうち、その国民の住む町からの距離が最も小さい町の店で文字を買い、あなたに献上する。

回文こそが最も美しい文字列であると信じるあなたは、指示により献上される文字を用いて作った回文を飾ることで歓迎の意を伝えようと思っています。 Q 個の整数組 (S_i, T_i) が与えられるので、 S_i, S_i+1, \ldots, T_i 日目に献上される文字を全て用い、適切に並び替えることで、回文を作ることができるかを判定してください。

制約

• 2 \leq N \leq 2 \times 10^5
• 1 \leq M \leq 2 \times 10^5
• 1 \leq Q \leq 2 \times 10^5
• 1 \leq A_i, B_i \leq N (1 \leq i \leq N-1)
• どの町からどの町へも 0 本以上の道路を通り移動できる
• 1 \leq C_i \leq N (1 \leq i \leq N)
• 1 \leq U_i \leq V_i \leq N (1 \leq i \leq M)
• 1 \leq L_i \leq R_i \leq N (1 \leq i \leq M)
• 1 \leq S_i \leq T_i \leq M (1 \leq i \leq Q)
• 入力は全て整数

小課題

1. (5 点) N \leq 300, M \leq 300, Q = 1, S_1 = 1, T_1 = M, C_i \leq 2 (1 \leq i \leq N)
2. (5 点) N \leq 2000, M \leq 2000, Q = 1, S_1 = 1, T_1 = M, C_i \leq 2 (1 \leq i \leq N)
3. (5 点) N \leq 2000, M \leq 2000, C_i \leq 2 (1 \leq i \leq N)
4. (5 点) A_i=i, B_i=i+1 (1 \leq i \leq N-1) ,C_i \leq 2 (1 \leq i \leq N)
5. (20 点) A_{i+1} = B_i (1 \leq i \leq N-2) ,C_i \leq 2 (1 \leq i \leq N)
6. (10 点) A_{i+1} = B_i (1 \leq i \leq N-2)
7. (40 点) C_i \leq 2 (1 \leq i \leq N)
8. (10 点) 追加の制約はない

入力例 1

5
1 2
1 3
3 4
3 5
1 2 1 2 1
3
1 5 2 4
2 4 1 3
3 3 5 5
1
1 3

出力例 1

Yes

パ研王国は以下のようになります。

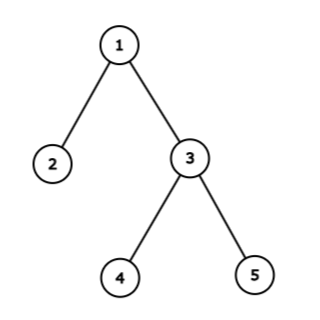
また、各日には次のような出来事が起こります。

• 1 日目は町 1, 3, 5 でパレードが開催されます。あなたは町 2, 3, 4 の住人に指示を出し、住人はそれぞれ町 1, 3, 3 で文字 1, 1, 1 を買います。
• 2 日目は町 2, 1, 3, 4 でパレードが開催されます。あなたは町 1, 2, 3 の住人に指示を出し、住人はそれぞれ町 1, 2, 3 で文字 1, 2, 1 を買います。
• 3 日目は町 3 でパレードが開催されます。あなたは町 5 の住人に指示を出し、住人はそれぞれ町 3 で文字 1 を買います。

よって、 1, 2, 3 日目に献上される文字を並び替えると、 1, 1, 1, 2, 1, 1, 1 という回文を作ることができます。

この入力例は小課題 1, 2, 3, 7, 8 の制約を満たします。

入力例 2

10
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
2 1 2 1 2 1 1 1 2 2
5
1 1 1 7
1 10 7 8
3 6 5 8
2 10 2 10
3 8 1 2
3
2 3
2 2
4 4

出力例 2

No
Yes
Yes

この入力例は小課題 3, 4, 5, 6, 7, 8 の制約を満たします。

入力例 3

7
5 7
7 4
4 6
6 2
2 3
3 1
1 2 2 1 1 1 1
3
1 2 5 5
5 7 2 4
1 7 5 5
2
1 2
1 3

出力例 3

No
Yes

この入力例は小課題 3, 5, 6, 7, 8 の制約を満たします。

入力例 4

5
1 2
1 3
1 4
1 5
2 1 2 2 3
2
1 4 3 5
1 1 2 3
5
1 2
1 2
1 1
1 2
1 2

出力例 4

Yes
Yes
Yes
Yes
Yes

この入力例は小課題 8 の制約を満たします。

問題文

パケン国には、年の初めに縦に餅を重ねた縁起物「ダブル餅」を飾る風習があります。このダブル餅は次の性質を持ちます。

• 上から順に重ねた餅の重さをそれぞれ V_1, V_2, \dots, V_n（餅の個数を n とする）としたとき、すべての i (1 \leq i \leq n-1) に対して 2 \times V_i \leq V_{i+1} が成り立つ。

パケン国の住民であるパケ子さんは 1 から N までの番号が付いた N 個の餅を持っています。餅 i (1 \leq i \leq N) の重さは W_i です。
ここで、全ての i (1 \leq i \leq N-1) について W_i \leq W_{i+1} が成り立ちます。 パケ子さんはあなたに Q 個の問い合わせをします。 i 番目の問い合わせは、「 L_i 番から R_i 番の番号が付いた餅全てをちょうど 1 つずつ使っていくつかのダブル餅を作るとき、最小でいくつのダブル餅を作ることになるか？」という内容です。それぞれに対して求める最小個数を回答してください。

制約

• 1 \leq N \leq 2 \times 10^5
• 1 \leq Q \leq 2 \times 10^5
• 1 \leq W_i \leq 10^9 (1 \leq i \leq N)
• 1 \leq L_i \leq R_i \leq N (1 \leq i \leq Q)
• W_i \leq W_{i+1} (1 \leq i \leq N-1)
• 入力は全て整数

小課題

1. (1 点) N \leq 6 , Q = 1
2. (4 点) N \leq 16 , Q = 1
3. (10 点) N \leq 2000 , Q = 1
4. (10 点) Q = 1
5. (75 点) 追加の制約はない

入力例 1

7 3
2 3 3 4 6 8 16
3 7
2 2
1 7

出力例 1

2
1
3

1 番目の問い合わせでは、使う餅の重さはそれぞれ 3,4,6,8,16 です。

• 重さが 3 と 6 の餅 を使ったダブル餅
• 重さが 4,8,16 の餅 を使ったダブル餅

このように 2 つのダブル餅を作ることで、作るダブル餅の個数は 2 個 となり、これが最小です。

2 番目の問い合わせでは、使う餅の重さは 3 のみです。この場合、作るダブル餅の個数は必ず 1 個 になります。
餅が 1 つだけでも、それ自体でダブル餅として扱うことに注意してください。

3 番目の問い合わせでは、使う餅の重さはそれぞれ 2,3,3,4,6,8,16 です。

• 重さが 3 と 6 の餅 を使ったダブル餅
• 重さが 2,4,8,16 の餅 を使ったダブル餅
• 重さが 3 の餅単体 で構成されるダブル餅

このように 3 個のダブル餅 を作ることで、作るダブル餅の個数は 3 個 となり、これが最小です。
このサンプルは小課題 5 の制約を満たします。

問題文

頂点 1 を根とする N 頂点の根付き木があり、頂点 i の親は P_i です。また、各頂点には 1 つの非負整数を書くことができます。

あなたは、まずこの木の全ての葉、すなわち子を 1 つも持たない頂点に 0 か 1 を書きます。その後、葉でない頂点全てに対し、その子の頂点に書かれた数の集合の \mathrm{mex} を書きます。

厳密には、頂点 v に書く非負整数を A_v としたとき、以下の条件を満たすようにします。

• 頂点 v が葉のとき、A_v = 0 または A_v = 1
• 頂点 v が葉でないとき、頂点 v の子を C_1,C_2,\ldots,C_M とすると、 A_v = \mathrm{mex}(\{A_{C_1},A_{C_2},\ldots,A_{C_M}\})

ただし、ある非負整数の集合 S に対し、 \mathrm{mex}(S) は S に含まれない最小の非負整数を表します。

葉の個数を L とすると、頂点への非負整数の書き方は 2^L 通りあります。k = 0,1,2,\ldots,N のそれぞれについて、 2^L 通りの書き方の中で最終的に頂点 1 に k が書かれるようなものの個数を 998244353 で割った余りを求めてください。

制約

• 1 \leq N \leq 2 \times 10^{5}
• 1 \leq P_i < i (2 \leq i \leq N)
• 入力は全て整数

小課題

1. (4 点) 葉の個数は 5 個以下
2. (8 点) P_i = 1 (2 \leq i \leq N)
3. (8 点) P_i = \lfloor \frac{i}{2} \rfloor (2 \leq i \leq N)
4. (15 点) N \leq 100
5. (25 点) N \leq 5000
6. (40 点) 追加の制約はない

入力例 1

5
1 1 2 2 

出力例 1

3
3
2
0
0
0

この入力例では、葉は頂点 3, 4, 5 です。例えば、これらにそれぞれ 0, 1, 0 を書いた場合、

• 頂点 2 の子は 頂点 4, 5 で、それぞれ 1, 0 が書かれているため、頂点 2 には \mathrm{mex}(\{0,1\}) = 2 を書きます。
• 頂点 1 の子は 頂点 2, 3 で、それぞれ 2, 0 が書かれているため、頂点 1 には \mathrm{mex}(\{0,2\}) = 1 を書きます。

よって、この場合頂点 1 に書かれる数は 1 です。

このサンプルは小課題 1,3,4,5,6 を満たします。

入力例 2

9
1 2 2 1 2 3 2 5 

出力例 2

15
15
2
0
0
0
0
0
0
0

このサンプルは小課題 1,4,5,6 を満たします。

問題文

フランス料理店「パケンシェ」のシェフであるパケン氏は、ディナータイムに備えて N 個の料理を用意し、左右一列に並べた。それぞれの料理は 1 以上 K 以下の整数で表されるおいしさという値を持っており、現在、左から i 番目の料理のおいしさは D_i である。パケンシェでは、おいしさがそれぞれ 1, 2, \ldots, K である料理をこの順で 1 つずつ提供するコース料理が非常に人気となっている。

訪れた客になるべく満足してもらうよう、パケン氏はこれら N 個の料理に対して以下のような Q 回の行動を行った。 i 回目の行動の種類は 1 以上 3 以下の整数 T_i で表され、それぞれ以下のような内容である。

• T_i = 1 の場合、料理の作り直しを行い、 L_i 番目から R_i 番目の全ての料理を、おいしさが V_i の料理に変更した。

• T_i = 2 の場合、料理にトッピングを行い、 L_i 番目から R_i 番目のおいしさが K 未満であった料理のおいしさを 1 増加させた。しかしながら、トッピング前においしさが K であった料理は非常に繊細な料理であったことから、おいしさが 1 に変化した。

• T_i = 3 の場合、次のような思考実験を行った：「ディナータイムに 10^{100} 人の客が来たとする。 L_i 番目から R_i 番目までの料理を、左の料理から順に誰か一人の客に提供する。このとき、おいしさがそれぞれ 1,2, \ldots, K である料理をこの順で 1 つずつ提供した客の人数を最大で何人にできるだろうか？」
  なお、この思考実験によって料理のおいしさが変化したり、料理がなくなることはない。

パケン氏の弟子であるあなたは、パケン氏の思考実験それぞれに対して、正しい答えを求める必要がある。

制約

• 1 \leq N, Q \leq 150000
• 1 \leq K \leq 5
• 1 \leq D_i \leq K (1 \leq i \leq N)
• T_i は 1, 2, 3 のいずれか
• 1 \leq L_i \leq R_i \leq N (1 \leq i \leq Q)
• T_i = 1 ならば、1 \leq V_i \leq K (1 \leq i \leq Q)
• 入力は全て整数

小課題

1. (1 点) K = 1
2. (9 点) N, Q \leq 2000
3. (30 点) K = 2
4. (15 点) T_i = 1, 3 (1 \leq i \leq Q)
5. (15 点) T_i = 2, 3 (1 \leq i \leq Q)
6. (30 点) 追加の制約はない

入力例 1

10 5
1 2 3 4 5 1 2 3 4 5
10
3 1 10
3 1 7
1 5 7 2
2 5 7
2 5 7
2 5 7
3 1 10
1 6 7 2
1 6 6 1
3 1 10

出力例 1

2
1
1
2

パケン氏は 10 個の料理を用意し、おいしさは順に (1, 2, 3, 4, 5, 1, 2, 3, 4, 5) になっています。これからパケン氏は 10 回の行動をします：

• 1 回目の行動では、 1 番目から 10 番目の料理における思考実験を行う。 1 番目から 5 番目の料理を 1 人目の客に提供し、6 番目から 10 番目の料理を 2 人目の客に提供することで、2 人の客にコース料理を提供することができる。3 人以上の客に提供することはできないので、答えは 2 となる。

• 2 回目の行動では、1 番目から 7 番目の料理における思考実験を行う。1 番目から 5 番目の料理を 1 人の客に提供することで、1 人の客にコース料理を提供することができる。2 人以上の客に提供することはできないので、答えは 1 となる。

• 3 回目の行動では、作り直しを行い 5 番目から 7 番目の料理をおいしさが 2 の料理に変更する。おいしさは順に (1, 2, 3, 4, 2, 2, 2, 3, 4, 5) になる。

• 4 回目の行動では、トッピングを行い 5 番目から 7 番目の料理のおいしさを 1 増加させる。おいしさは順に (1, 2, 3, 4, 3, 3, 3, 3, 4, 5) になる。

• 5 回目の行動では、トッピングを行い 5 番目から 7 番目の料理のおいしさを 1 増加させる。おいしさは順に (1, 2, 3, 4, 4, 4, 4, 3, 4, 5) になる。

• 6 回目の行動では、トッピングを行い 5 番目から 7 番目の料理のおいしさを 1 増加させる。おいしさは順に (1, 2, 3, 4, 5, 5, 5, 3, 4, 5) になる。

• 7 回目の行動では、1 番目から 10 番目の料理における思考実験を行う。1 番目から 5 番目の料理を 1 人の客に提供することで、1 人の客にコース料理を提供することができる。2 人以上の客に提供することはできないので、答えは 1 となる。

• 8 回目の行動では、作り直しを行い 6 番目から 7 番目の料理をおいしさが 2 の料理に変更する。おいしさは順に (1, 2, 3, 4, 5, 2, 2, 3, 4, 5) になる。

• 9 回目の行動では、作り直しを行い 6 番目から 6 番目の料理をおいしさが 1 の料理に変更する。おいしさは順に (1, 2, 3, 4, 5, 1, 2, 3, 4, 5) になる。

• 10 回目の行動では、 1 番目から 10 番目の料理における思考実験を行う。 1 番目から 5 番目の料理を 1 人目の客に提供し、6 番目から 10 番目の料理を 2 人目の客に提供することで、2 人の客にコース料理を提供することができる。3 人以上の客に提供することはできないので、答えは 2 となる。

問題文

この問題はインタラクティブな問題です。

パ研王国には N 個の交差点があり、1 から N までの番号が付いています。また、M 本の道があり、それぞれの道は 2 個の異なる交差点を双方向に結んでいます。2 本の異なる道が同じ交差点の組を結ぶことはありません。

これらの道には 1 以上 K 以下の整数で表される色が塗られています。複数の道が同じ色で塗られているかもしれません。ただし、ある交差点につながれた道の中に、同じ色の道が 2 本以上存在することはありません。

茜さんは、交差点を移動するロボットを開発しました。このロボットには、(1, 2, \ldots, K) を並び替えることで得られる数列 P = (P_1, P_2, \ldots, P_K) を与えて操作します。ロボットは今いる頂点につながれた道のうち、その色が P に一番最初に出現するようなものを選び、その道に沿って移動します。(追記: 12:40) この移動は 1 回の操作につき 1 度のみ行われます。

茜さんは交差点の数 N および色の種類数 K のみを知っています。そこで茜さんは以下の 調査 を最大 10000 回行うことで、道の数 M と各道がつなぐ交差点の番号、および各道の色を特定したいです。

調査: 頂点 v を選びそこにロボットを配置する。その後ロボットに P = (P_1, P_2, \ldots, P_K) を与えて操作して、ロボットの移動先の交差点の番号を調べる。

ただし、茜さんは非常に忙しいため調査の回数はできるだけ少なくしたいです。

茜さんの戦略を実装したプログラムを作成してください。

制約

• 3 \leq N \leq 500
• N - 1 \leq M \leq 500
• 2 \leq K \leq 500
• どの交差点からどの交差点へも、0 本以上の道を経由して移動できる

小課題

1. (3 点) N=3, M=2, K=2, \mathrm{subtask\_id} = 1
2. (3 点) N=3, M=2, \mathrm{subtask\_id} = 2
3. (4 点) K=2, \mathrm{subtask\_id} = 3
4. (90 点) \mathrm{subtask\_id} = 4 。この小課題では，以下に従い得点が決定される。
   • この小課題に対応するテストケースについて，1 つでも AC でない判定を得たものがあった場合、この小課題の得点は 0 点となる。
   • そうでない場合、この小課題のすべてのテストケースにおける、調査の回数の最大値を Q とする。このとき、小課題の得点は以下のように決定される。
     • 8750 < Q \leq 10000 のとき 5 点
     • 5003 < Q \leq 8750 のとき \left\lfloor\frac{20000}{Q - 4750}\right\rfloor 点
     • 5000 < Q \leq 5003 のとき 90 - (Q - 5000) \times 3 点
     • Q \leq 5000 のとき 90 点

入出力

最初に、交差点の数 N 、色の種類数 K、小課題の番号 \mathrm{subtask\_id} が以下の形式で入力で与えられる。

N K \mathrm{subtask\_id}

次に、あなたは 10000 回以下調査を行う。 v と P = (P_1, P_2, \ldots, P_K) は、標準出力に以下の形式で出力されなければならない。

? v P_1 P_2 \ldots P_K

ここで v は 1 \leq v \leq N を満たす整数である必要がある。また、(P_1, P_2, \ldots, P_K) は (1, 2, \ldots, K) を並び替えて得られる数列でなければならない。

次に、クエリの答えが標準入力から以下の形式で与えられる。

\mathrm{ans}

ここで \mathrm{ans} は 1 以上 N 以下の整数で、ロボットが移動した先の交差点の番号を表す。

最後に、答えを以下の形式で出力しなければならない。

!
M
A_1 B_1 C_1
A_2 B_2 C_2
\vdots
A_M B_M C_M

ここで M は道の本数、A_i と B_i は道の両端の交差点の番号、C_i は道の色を表す。

ただし、道を出力する順番、および A_i と B_i の順番は任意である。

ジャッジ

• 出力のあと、標準出力を flush しなければならない。 そうしない場合、ジャッジ結果は不定である。

• 答えを出力した後、プログラムをすぐに終了しなければならない。そうでないときの挙動は定義されていない。

• 不正な質問や不正な出力を行った場合、ジャッジ結果は不定である。

入出力例

以下の例は意味をもつやりとりとは限らない。

採点に関する注意

すべてのテストケースについて，実際の採点プログラムは適応的 (adaptive) ではない。これは、採点プログラムは初めから固定された道の情報を持つということを意味する．

問題文

パ研王国には N 人の住人がいて、1 から N までの番号がつけられています。パ研王国の住人には競技プログラミングの強さを表すレーティングという値が定められていて、住人 i (1 \leq i \leq N) のレーティングは R_i です。

また、この N 人の間には M 個の友達関係があり、住人 A_j と住人 B_j (1 \leq j \leq M) は友達です。この M 個の友達関係以外に友達である住人の組は存在しません。

パ太郎はパ研王国の住人を対象に競技プログラミングのコンテストを開くことにしました。パ太郎はまずレーティング制限X (X は整数) を定め、その後 N 人の住人のうち K 人を任意に選び、招待状を送ることにしました。

パ太郎または他の住人から招待状を受け取った住人 x (1 \leq x \leq N) は次のように行動します。

• 既に 1 枚以上の招待状を受け取っていた場合、何もしない。
• それまでに招待状を受け取っておらず、自身のレーティングがレーティング制限以上である場合、すなわち X \leq R_x の場合、コンテストに参加し、さらに自分の友達であるような住人全員に新たに招待状を送る。
• それ以外の場合、何もしない。

パ太郎はコンテストのレベルを高めるためできるだけレーティング制限を大きくしたいですが、参加者が少なすぎると困ってしまいます。

そこでパ太郎は N 個の質問を考えました。k (1 \leq k \leq N) 番目の質問は、次のようなものです。

• k 人以上の住人がコンテストに参加するためにはレーティング制限を最大でいくつにできるだろうか？ただし、招待状を送る K 人の住人は自由に選べるものとする。

パ太郎のために、この N 個の質問に答えるプログラムを作成してください。

制約

• 1 \leq N \leq 2 \times 10^5
• 0 \leq M \leq 2 \times 10^5
• 1 \leq K \leq N
• 1 \leq R_i \leq 10^{18} (1 \leq i \leq N)
• 1 \leq A_i<B_i \leq N (1 \leq i \leq M)
• (A_i,B_i) \neq (A_j,B_j) (i \neq j)
• 入力は全て整数

小課題

1. (1 点) N \leq 2
2. (2 点) M = 0
3. (2 点) N \leq 10
4. (10 点) R_i = 1 (1 \leq i \leq N)
5. (10 点) R_i \leq 5 (1 \leq i \leq N)
6. (20 点) K = 1
7. (30 点) K \leq 5
8. (25 点) 追加の制約はない

入力例 1

4 3 1
1 2 3 4
1 2
2 3
3 4

出力例 1

4
3
2
1

例えば、 k=3 のとき、 X=2 とすれば条件を満たすことができます。具体的には、住人 2 に招待状を送ると、住人 2 が住人 3 に、住人 3 が住人 4 に招待状を送るため、最終的には住人 2,3,4 の 3 人が参加することで条件を満たします。なお、住人 2 は住人 1 にも招待状を送りますが、住人 1 のレーティングは X 未満であるため、住人 1 はコンテストには参加しません。

このサンプルは小課題 3, 5, 6, 7, 8 の制約を満たします。

入力例 2

4 0 2
4 3 2 1

出力例 2

4
3
-1
-1

入力例 3

4 2 2
1 1 1 1
1 3
2 4

出力例 3

1
1
1
1