Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
伊香保温泉の温泉街には 365 段の石段があることで知られています。 この石段の各段と一般的なカレンダーにおける平年の日付を対応づけることを考えます。
1 月 1 日を 1 段目、1 月 2 日を 2 段目、\cdots、12 月 31 日を 365 段目に対応づけたとき、パ研合宿2024の N 日目は何段目に対応するか求めてください。
制約
- 1 \leq N \leq 4
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを出力せよ。
入力例 1
1
出力例 1
89
パ研合宿2024の 1 日目は 3 月 30 日で、石段の 89 段目に対応します。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 100 点
問題文
パ研商店では、P, A, K, E, N, C, A, M, P の文字が書かれたパネル計 9 枚を 1 つのセットにして販売しています。(同じ文字のパネルが複数枚含まれていることに注意してください。)
パンダのパ太郎はこのセットをいくつか買い、買ったパネルのうち何枚かを選んでそれらを自由に並べることで長さ N の文字列 S を作りたいと考えています。
パ太郎が S を作るために買う必要があるセットの数の最小値を求めてください。
ただし、セットをいくつ買っても S を作ることができない場合はそのことを報告してください。またパ研商店の在庫は十分多いものとします。
制約
- 1 \leq N \leq 10^5
- S は英大文字からなる長さ N の文字列
- N は整数
入力
入力は以下の形式で標準入力から与えられる。
N S
出力
S を作るために買う必要があるセットの数の最小値を出力せよ。
ただし、セットをいくつ買っても S を作ることができない場合は -1 と出力せよ。
入力例 1
7 PANCAKE
出力例 1
1
PANCAKE を作るためには P が 1 つ、 A が 2 つ、 N が 1 つ、 C が 1 つ、 K が 1 つ、 E が 1 つ必要です。セットを 1 セット買うことでこれらの文字を全て揃えることができます。
入力例 2
5 PEACE
出力例 2
2
入力例 3
5 IKAHO
出力例 3
-1
Time Limit: 2.5 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
長さ N の数列 A = (A_1,A_2,\ldots,A_N) と Q 個の整数の組 (L_i,R_i) (1 \leq L_i \leq R_i \leq N) が与えられます。 i = 1,2,\ldots,Q について次の問題を解いてください。
- 数列 A の要素を添字 L_i から順に足していくとき、その和が初めて添字 R_i までの総和の半分を超える位置、つまり \displaystyle\sum_{k=L_i}^{n} A_k > \frac{1}{2} \displaystyle\sum_{k=L_i}^{R_i} A_k を満たす最小の正整数 n を出力してください。
制約
- 1 \leq N \leq 2 \times 10^5
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq A_i \leq 10^9 (1 \leq i \leq N)
- 1 \leq L_i \leq R_i \leq N (1 \leq i \leq Q)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N Q L_1 R_1 L_2 R_2 \vdots L_Q R_Q
出力
Q 行出力せよ。 i 行目 (1 \leq i \leq Q) には、 i 番目の問題の答えを出力せよ。
入力例 1
4 2 3 5 7 4 1 2 1 3 2 4 1 4
出力例 1
2 3 3 3
例えば i=2 のとき、 \displaystyle\sum_{k=1}^{3} A_k = 2 + 3 + 5 = 10 です。
- n=1 のとき、 \displaystyle\sum_{k=1}^{1} A_k = 2 より、 2 \leq \frac{1}{2} \times 10 なので条件を満たしません。
- n=2 のとき、 \displaystyle\sum_{k=1}^{2} A_k = 5 より、 5 \leq \frac{1}{2} \times 10 なので条件を満たしません。
- n=3 のとき、 \displaystyle\sum_{k=1}^{3} A_k = 10 より、 10 > \frac{1}{2} \times 10 なので条件を満たします。
以上より、 3 を出力してください。
入力例 2
5 1000000000 1000000000 1000000000 1000000000 1000000000 1 1 5
出力例 2
3
総和が 32 bit整数に収まらない計算がある場合に注意してください。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
頂点 1, 2, \ldots, N の N 頂点からなる無向グラフがあります。
全ての整数 u, v (1 \leq u < v \leq N) に対し、 u と v が互いに素なとき頂点 u と v の間に辺が張られており、またこれ以外に辺はありません。
頂点 S から頂点 T まで移動するのに通る必要がある辺の個数の最小値を求めてください。
制約
- 2 \leq N \leq 10^{18}
- 1 \leq S, T \leq N
- S \neq T
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N S T
出力
答えを出力せよ。
入力例 1
4 2 4
出力例 1
2
グラフは以下のようになります。
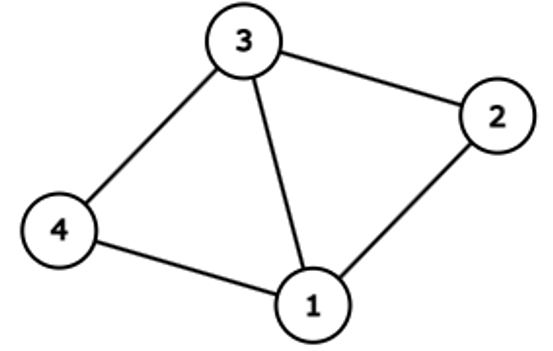
2 \to 3 \to 4 と移動したとき、通る辺の個数は 2 本です。また 1 本以下で移動することはできないため、 2 を出力します。
入力例 2
9999999999 1000000007 998244353
出力例 2
1
入力は 32bit 整数型に収まらない可能性があることに注意してください。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 200 点
問題文
数直線上に 1,2, \ldots, N と番号がついた N 匹のヤギがいます。ヤギ i ははじめ座標 A_i にいます。ここで、ヤギははじめ相異なる座標にいることが保証されます。
以下の Q 個のクエリを i=1,2,\ldots,Q の順に処理してください。
座標 B_i に先生がエサを置き、エサからの距離が最も小さいヤギがエサを食べます。ただし、そのようなヤギが複数いる場合は、そのようなヤギの中で番号が最も小さいヤギがエサを食べます。また、座標 X と座標 Y の距離は \lvert X-Y \rvert であるとします。
それぞれのエサを食べるヤギの番号を求めてください。ただし、エサを食べたヤギはエサのある座標に移動し、そのままそこに残るものとします。
制約
- 1 \leq N,Q \leq 2 \times 10^5
- -10^{18} \leq A_i \leq 10^{18} (1 \leq i \leq N)
- A_i \neq A_j (1 \leq i < j \leq N)
- -10^{18} \leq B_i \leq 10^{18} (1 \leq i \leq Q)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N Q B_1 B_2 \ldots B_Q
出力
各クエリに対して 1 行で答えを出力せよ。
入力例 1
5 10 7 21 2 13 4 11 9 17 16
出力例 1
1 1 3 3
1 つ目のクエリでは、エサが置かれる 11 に最も近い 10 にいるヤギ 1 がエサを食べ、 11 に移動します。
2 つめのクエリでは、エサが置かれる 9 に近いヤギは 7 にいるヤギ 2 と 11 にいるヤギ 1 がいます。そのため、より番号の小さいヤギ 1 がエサを食べ、 9 に移動します。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 300 点
問題文
正整数 N が与えられます。以下の条件を満たす単純無向グラフが存在するか判定してください。
- 頂点の個数を M とし、頂点 i\ (1 \le i \le M) の次数を d_i とする。この時、 M\times d_1 \times d_2 \times \ldots \times d_M = N である。
制約
- 1 \leq N \leq 10^9
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N
出力
存在する場合は Yes を、存在しない場合は No を出力せよ。
入力例 1
3
出力例 1
No
条件を満たすグラフは存在しません。
入力例 2
12
出力例 2
Yes
以下のようなグラフが条件を満たします。
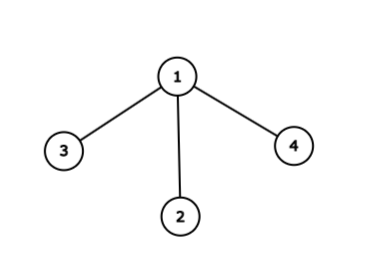
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
以下を満たす数列 A の M 項目を 998244353 で割った余りを求めてください。
- A_{1} = N
- 正整数kに対してA_{k+1} = A_{k} + f(A_{k})
ここで、f(x) で x の x でない最大の約数を表します。
制約
- 2 \leq N \leq 10^{12}
- 1 \leq M \leq 10^{18}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M
出力
数列 A の M 項目を 998244353 で割った余りを出力せよ。
入力例 1
4 3
出力例 1
9
A_1=4 です。
f(4)=2 より、 A_2=A_1+f(A_1)=4+2=6 です。
f(6)=3 より、 A_3=A_2+f(A_2)=6+3=9 です。
よって、答えるべき値は 9 です。
入力例 2
3 1
出力例 2
3
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
N 個のライトと \frac{N(N+1)}{2} 個のボタンがあります。1 \leq l \leq r \leq N を満たすすべての整数の組 (l,r) に対して、 (l,r) に対応するボタンが 1 つずつあります。各ライトは点灯しているか消灯しているかのどちらかです。
(l,r) に対応するボタンを押すと l 個目, l+1 個目, \ldots, r 個目のライトについて点灯している場合は消灯し、消灯している場合は点灯します。このとき、他のライトには何も起きません。
N 個のライトが点灯しているか消灯しているかの状態は 2^N 通りあります。それぞれの状態から N 個すべてのライトを点灯させるためにボタンを押す必要がある回数の最小値の総和を 998244353 で割ったあまりを求めてください。
制約
- 1 \leq N \leq 10^{100000}
- 入力は全て整数
小課題
- ( 50 点 ) N \leq 10^6
- ( 200 点 ) N \leq 10^{18}
- ( 150 点 ) 追加の制約はない。
入力
入力は以下の形式で標準入力から与えられる。
N
出力
答えを出力せよ。
入力例 1
4
出力例 1
20
例えば、2 個目のライトが点灯している状態からすべてのライトを点灯させる場合、 (1,4) に対応するボタンを押した後、 (2,2) に対応するボタンを押すことで 2 回で達成することができます。
ボタンを 1 回以下押して 2 個目のライトが光っている状態からすべてのライトを点灯させることができないため、ボタンを押す必要がある回数の最小値は 2 です。
入力例 2
1
出力例 2
1
入力例 3
2025
出力例 3
697188344
998244353 で割ったあまりを求めることを忘れないでください。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
正整数 A,B が与えられます。
A,B に以下の 4 種類の操作を好きな順番で何度でも行うことができます。
- A の操作前の値を x としたとき、 2x+1 に変える
- A の操作前の値を x としたとき、 2x-1 に変える
- B の操作前の値を x としたとき、 2x+1 に変える
- B の操作前の値を x としたとき、 2x-1 に変える
操作を 0 回以上行うことで A=B にすることができるか判定してください。
T 個のテストケースが与えられるので、それぞれについて判定してください。
制約
- 1 \leq T \leq 10^5
- 1 \leq A,B \leq 10^{18}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T case_1 case_2 \vdots case_T
各テストケースは以下の形式で与えられる。
A B
出力
それぞれのテストケースについて、 A=B にすることができる場合は Yes 、そうでない場合は No を出力せよ。
入力例 1
5 3 23 4 7 4 9 1 1000000000000000000 5 13
出力例 1
Yes Yes Yes Yes No
1 つ目のケースでは、 2 個目の操作を 1 回加えた後、 1 個目の操作を 2 回加えることで A=B にすることができます。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
長さ N の非負整数列 A,B が与えられます。あなたは以下の操作を 0 回以上任意の回数行うことができます。
- 1\le l\le r\le N を満たす整数対 (l,r) を選ぶ。コスト x を払い、 l\le i\le r を満たすすべての i に対して、 A_i を A_i \lor x に置き換える。
操作後に A=B とすることが可能か判定し、可能ならば払うコストの総和の最小値を求めてください。
ただし、 a \lor b で a と b の bitwise or を表すものとします。
制約
- 1 \leq N \leq 2\times 10^5
- 0 \leq A_i < 2^{30} (1 \leq i \leq N)
- 0 \leq B_i < 2^{30} (1 \leq i \leq N)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N A_1 A_2 \ldots A_N B_1 B_2 \ldots B_N
出力
不可能ならば、 -1 を出力せよ。可能ならば、答えを出力せよ。(2:33 追記)
入力例 1
3 4 4 2 5 6 7
出力例 1
8
最初に (l,r)=(2,2),x=2 として A_2=6 とし、次に (l,r)=(1,1), x=1 として A_1=5 とし、最後に (l,r)=(3,3),x=5 として A_3=7 とすると A=B となり、コストの総和 8 で達成することができます。コストの総和 7 以下で A=B とすることは不可能なので、 8 を出力します。
入力例 2
3 2 2 2 1 1 1
出力例 2
-1
入力例 3
5 339062933 763623855 531094908 999489902 213141341 884846815 1068498863 1072160639 1000064367 519438175
出力例 3
859176523
入力例 4
6 0 0 0 0 0 0 1073741823 0 1073741823 0 1073741823 0
出力例 4
3221225469
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
1 辺の長さが N の立方体を、 N^3 個の 1 辺の長さが 1 の立方体のピースに分割します。この中から次の条件を満たすようにいくつかのピースを選ぶ方法のうち、選ぶ個数が最も小さいものを一つ構築してください。
- 立方体の面に垂直な 3 方向のうちどの方向から見ても、穴が隣接していない。
ここである方向から見たときの穴とは、ピース N 個が重なって見える 1 辺の長さが 1 の正方形のうち、それら N 個のピースが一つも選ばれていないものを指します。また、 2 つの穴が隣接するとは、それらが辺を共有することを指します。
より厳密には、分割後のピースを 3 整数の組 (x_i,y_i,z_i) に対応させた時、m を選んだ立方体の個数として、3 整数の組の集合 S = \{(x_1,y_1,z_1), (x_2,y_2,z_2), \ldots, (x_m,y_m,z_m)\} (1 \leq x_i,y_i,z_i \leq N) で以下の条件を全て満たすもののうち m が最小となるものを 1 つ構築してください。
- 全ての整数 y, z, y', z' (1 \leq y, z, y', z' \leq N, \lvert y-y' \rvert + \lvert z - z' \rvert = 1) に対し、 (x, y, z) \in S または (x, y', z') \in S を満たす整数 x (1 \leq x \leq N) が存在する。
- 全ての整数 z, x, z', x' (1 \leq z, x, z', x' \leq N, \lvert z-z' \rvert + \lvert x - x' \rvert = 1) に対し、 (x, y, z) \in S または (x', y, z') \in S を満たす整数 y (1 \leq y \leq N) が存在する。
- 全ての整数 x, y, x', y' (1 \leq x, y, x', y' \leq N, \lvert x-x' \rvert + \lvert y - y' \rvert = 1) に対し、 (x, y, z) \in S または (x', y', z) \in S を満たす整数 z (1 \leq z \leq N) が存在する。
なお、この問題の制約下でこれらの条件を満たす選び方が存在することが証明できます。
制約
- 1 \leq N \leq 1000
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられます。
N
出力
答えを以下の形式で出力せよ。
m x_1 y_1 z_1 x_2 y_2 z_2 \vdots x_m y_m z_m
解が複数存在する場合、どれを出力しても正解とみなされる。
入力例 1
2
出力例 1
2 1 1 2 2 2 1
下の図のようになります。

3 方向いずれから見ても穴が隣り合っていることはありません。
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
パ研王国には N 個の町 1, 2, \ldots, N と、異なる 2 つの町を双方向に繋ぐ M 個の道路 1, 2, \ldots, M があります。道路 i (1 \leq i \leq M) は町 A_i と町 B_i を双方向に繋いでおり、 2 つの異なる道路が同じ町の組を結ぶことはありません。どの町からどの町へも 0 本以上の道路を通り移動できますが、道路以外を通って町から町へ移動することはできません。
さて、今年もパ研合宿の季節がやってきました。パ研合宿は町 1 で開催されるため、全ての町から参加者が町 1 に移動します。荷物を持って移動するのは大変なので、参加者はタクシーを使って町を移動することになりました。
パ研王国には N 個のタクシー会社 1, 2, \ldots, N があり、それぞれの会社には以下のような規則があります。
- タクシー会社 i のタクシーには、町 i からのみ乗車できる。
- タクシー会社 i のタクシーの運賃は、移動した距離によらず C_i である。
- タクシー会社 i のタクシーは、乗車してから最大 R_i 本の道路しか通ることができない。
複数のタクシーを乗り継ぐこともできますが、タクシー以外の手段で町を移動してはいけません。
参加者のために、それぞれの町からタクシーのみを用いて町 1 に移動するために必要な運賃の合計の最小値を求めてください。なお、この制約下で全ての町からタクシーのみを用いて町 1 に移動できることが証明できます。
制約
- 2 \leq N \leq 2 \times 10^5
- 1 \leq M \leq 2 \times 10^5
- 1 \leq A_i < B_i \leq N (1 \leq i \leq M)
- (A_i, B_i) \neq (A_j, B_j) (1 \leq i < j \leq M)
- どの町からどの町へも 0 本以上の道路を通り移動できる
- 1 \leq C_i \leq 10^9 (1 \leq i \leq N)
- 1 \leq R_i \leq 10 (1 \leq i \leq N)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 A_2 B_2 \vdots A_M B_M C_1 C_2 \ldots C_N R_1 R_2 \ldots R_N
出力
N 行出力せよ。 i 行目 (1 \leq i \leq N) には、町 i から町 1 にタクシーのみを用いて移動するのに必要な運賃の合計の最小値を出力せよ。
入力例 1
5 5 1 2 2 3 3 4 4 5 2 5 100 300 500 200 100 1 2 1 3 1
出力例 1
0 300 700 200 300
パ研王国は以下のようになります。
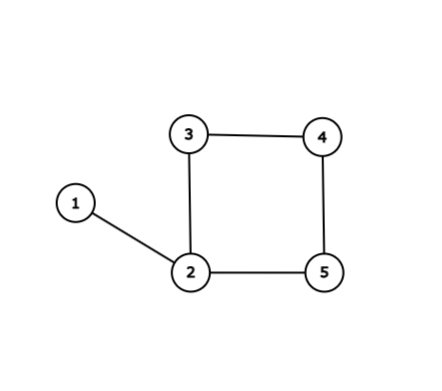
例えば、町 5 から町 1 へは以下のように移動できます。
- 町 5 でタクシー会社 5 のタクシーに乗り、町 4 まで移動する。
- 町 4 でタクシー会社 4 のタクシーに乗り、町 1 まで移動する。
このときに必要な運賃の合計は 100+200=300 です。運賃の合計が 300 未満となる移動方法はないため、 300 を出力します。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 500 点
問題文
以下の条件をすべて満たす英大文字からなる長さ 2N の文字列 S としてありえるものの個数を 998244353 で割った余りを求めよ。
- どの隣接している文字も同じでない。
- 最初の N 文字と最後の N 文字が一致しない。具体的には、 S_1 \neq S_{N+1}, S_2 \neq S_{N+2}, \ldots, S_N \neq S_{2N} のいずれかが成り立つ。
- 1 以上 K 以下の整数 i について、 S_{A_i}=C_i を満たす。
制約
- 1 \leq N \leq 10^9
- 0 \leq K \leq 10^5
- 1 \leq A_i \leq 2N (1 \leq i \leq K)
- A_i < A_{i+1} (1 \leq i \leq K-1)
- C_i (1 \leq i \leq K) はすべて英大文字
- N, K, A_i (1 \leq i \leq K) はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N K A_1 C_1 A_2 C_2 \vdots A_K C_K
出力
答えを出力せよ。
入力例 1
2 2 1 T 4 A
出力例 1
600
例えば、 TUNA のような文字列は条件を満たしますが、 TATA , TTTA のような文字列は条件を満たしません。
入力例 2
3 4 1 B 2 E 3 E 4 T
出力例 2
0
残りの部分にどのような文字を入れても 2 文字目と 3 文字目が同じであるため、条件を満たすことはありません。
入力例 3
1 0
出力例 3
650
入力例 4
6 2 4 O 7 S
出力例 4
606171726
答えを 998244353 で割った余りを求めることを忘れないでください。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
素数 P および正整数 H,W が与えられます。以下の問題を K=1,2,\ldots ,W について解いてください。
碁盤の目状のパ研王国には南から順に 0,1, \ldots H と番号が付いた H+1 本の東西方向の道路と、西から順に 0,1, \ldots W と番号が付いた W+1 本の南北方向の道路があります。
以降、 i 本目の東西方向の道路と j 本目の南北方向の道路の交わる交差点を (i,j) と表記します。
highlighter君の家は (0,0) にあり、 (H,W) にある学校まで東、または北に 1 区画分進むことを繰り返して通学します。南や西に進むことはできません。
しかし、太陽が眩しいため、 K 区画分より多く連続して東に進むことはできません。
条件を満たす通学路の個数を求めてください。ただし答えは非常に大きくなり得るので P で割った余りを出力してください。
制約
- 1 \leq H,W \leq 10^{6}
- 10^{8} \leq P \leq 10^{9}
- P は素数
- 入力は全て整数
小課題
- ( 200 点 ) H,W \leq 2000
- ( 400 点 ) 追加の制約はない。
入力
入力は以下の形式で標準入力から与えられる。
H W P
出力
W 行出力せよ。 i 行目には K=i の場合の答えを出力せよ。
入力例 1
8 5 998244353
出力例 1
126 882 1206 1278 1287
入力例 2
289 17 998244353
出力例 2
185944034 575259088 157522078 750432611 294726854 977803727 513648158 653193164 809039201 300639291 136301002 621883169 824367261 6666205 18818655 18902465 18902755
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
H \times W の格子点のうち相異なる3点を結んでできる三角形の個数を求めてください。
より厳密には、次の条件を満たす二次元平面上の3点の組 (X_1,Y_1),(X_2,Y_2),(X_3,Y_3) の個数を求めてください。
- 0 \leq X_1,X_2,X_3 < H
- 0 \leq Y_1,Y_2,Y_3 < W
- X_1,Y_1,X_2,Y_2,X_3,Y_3 は整数
- (X_1,Y_1),(X_2,Y_2),(X_3,Y_3) は相異なる
- (X_1,Y_1),(X_2,Y_2),(X_3,Y_3) を結んでできる図形は非退化な三角形である
ただし、並べ替えにより同じ組が得られる場合は1つの組とみなします。 また、答えは非常に大きくなる可能性があるため、 998244353 で割った余りを出力してください。
制約
- 2 \leq H,W \leq 10^{5}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
H W
出力
答えを 998244353 で割った余りを出力せよ。
入力例 1
2 2
出力例 1
4
例えば、(0,0),(0,1),(1,0) を結ぶと非退化な三角形が得られます。 2×2 の格子点から 3 点を選んで非退化な三角形を作る方法は 4 通りです。よって 4 を出力してください。
入力例 2
5 6
出力例 2
3820
入力例 3
128 256
出力例 3
353626996
答えを 998244353 で割った余りを出力してください。
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
縦 H 行、横 W 列のマス目があります。以下、左上のマスを (1, 1) とし、上から x 行目、左から y 列目のマスを (x, y) とします。
このマス目の上に長方形の構造物が N 個立っています。 i 個目の構造物は、 U_i \leq x \leq D_i, L_i \leq y \leq R_i を満たすマス (x, y) をすべて覆っており、それ以外のマスは覆っていません。ここで、 1 つのマスを覆う構造物はたかだか 1 つであることが保証されています。また、それぞれの構造物は値 C_i を持っています。
それぞれのマスの価値を、そのマスを覆う構造物の値と定義します。ただし、マスを覆う構造物が存在しない場合、そのマスの価値は 0 であるとします。
Falcon君は、発射した位置から右にあるマスを全て破壊する波動砲を持っています。厳密には、マス (x, y) で波動砲を発射すると、 y \leq j \leq W を満たす全ての整数 j について、マス (x, j) を破壊することができます。
このとき、Falcon君の嬉しさは破壊したマスの価値の合計となります。
この波動砲は上下には自由に動かすことができますが、左右には動かすことができません。波動砲を設置する列の候補を Q 個定め、それぞれ K_i 列目としました。それぞれの場合においてFalcon君の嬉しさの最大値を求めてください。
制約
- 1 \leq N \leq 10^5
- 1 \leq H,W \leq 10^9
- 1 \leq U_i \leq D_i \leq H (1 \leq i \leq N)
- 1 \leq L_i \leq R_i \leq W (1 \leq i \leq N)
- 2 つ以上の構造物が同じマスを覆うことはない
- 1 \leq C_i \leq 10^9 (1 \leq i \leq N)
- 1 \leq Q \leq 2 \times 10^5
- 1 \leq K_i \leq W (1 \leq i \leq Q)
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N H W U_1 D_1 L_1 R_1 C_1 U_2 D_2 L_2 R_2 C_2 \vdots U_N D_N L_N R_N C_N Q K_1 K_2 \vdots K_Q
出力
答えを出力せよ。
入力例 1
4 6 14 1 5 1 2 3 4 6 3 4 4 2 4 5 7 8 1 1 4 13 3 4 1 5 11 13
出力例 1
38 27 9 3
マス目は以下のようになります。
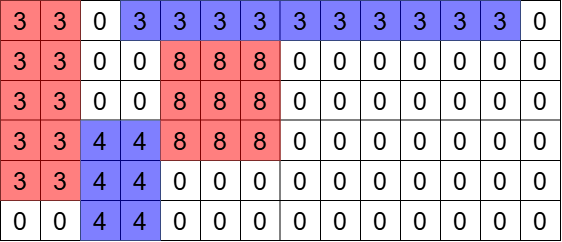
例えば 1 列目から発射する場合、
- 1 行目に設置した場合、嬉しさは 36
- 2 行目に設置した場合、嬉しさは 30
- 3 行目に設置した場合、嬉しさは 30
- 4 行目に設置した場合、嬉しさは 38
- 5 行目に設置した場合、嬉しさは 14
- 6 行目に設置した場合、嬉しさは 8
となるため、 38 を出力してください。
入力例 2
10 100 100 69 94 13 36 36 37 83 82 86 31 20 32 60 60 14 56 63 57 58 93 87 92 68 70 72 88 90 76 95 75 55 66 2 3 74 2 7 77 92 30 82 83 67 74 37 21 76 52 53 4 10 93 29 57 6 82 88 95 79 59 3
出力例 2
225 2004 1716 2580 1050 600 75 1275 1716 2580
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
以下の問題の答えを f(K) とします。
(1,2,\ldots,K) の順列 P=(P_{1},P_{2}, \ldots ,P_{K}) を考えます。 P が以下の条件をすべて満たすとき、それを ヒープ的な 順列と呼ぶことにします。
2P_{i} \leq P_{2i} \left(1 \leq i \leq \left\lfloor \frac{K}{2} \right\rfloor \right)
2P_{i} \leq P_{2i+1} \left(1 \leq i \leq \left\lfloor \frac{K-1}{2} \right\rfloor \right)
ヒープ的な順列の個数を求めてください。
N が与えられるので、 f(1)+f(2)+ \cdots +f(N) を 998244353 で割った余りを求めてください。
1 つの入力につきテストケースは T 個あります。
制約
- 1 \leq T \leq 10^{6}
- 1 \leq N \leq 10^{18}
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\mathrm{case}_{1}
\mathrm{case}_{2}
\vdots
\mathrm{case}_{T}
各テストケースは以下の形式で与えられる。
N
出力
T 行出力せよ。 i 行目には i 番目のテストケースに対する答えを出力せよ。
入力例 1
3 6 1 1000
出力例 1
9 1 465040340
例えば K=5 のとき、 P=\lbrace 1,2,3,5,4 \rbrace はヒープ的な順列です。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
パ研王国には 1 から N までの番号が付けられた N 個の町と町の間をつなぐ水道管が M 本あります。i 本目の水道管は町 U_i と V_i の間を結び、最大で水を W_i だけ流すことができます。また、水道管はどちらの方向にも流すことができます。任意の 2 つの町の間には高々 1 本の水道管が通っており、任意の 2 つの町の間は水道管を通って到達可能です。
1 以上 N 以下の異なる 2 つの整数 i,j について、f(i,j) を町 i から町 j へ流せる水の量の最大値とします。
このとき、(1,2,\ldots,N) の順列 P=(P_1,P_2,\ldots ,P_N) のうち、すべての 1 以上 N 以下の整数 i について P_i \neq i を満たすものについて \displaystyle \sum_{i=1}^{N} f(i,P_i) の最大値を求めてください。
制約
- 2 \leq N \leq 100
- N-1 \leq M \leq 200
- 1 \leq U_i,V_i \leq N (1 \leq i \leq M)
- U_i \neq V_i (1 \leq i \leq M)
- 1 \leq W_i \leq 10^5
- 任意の 2 つの町の間には高々 1 本の水道管が通っている
- 任意の 2 つの町の間は水道管を通って到達可能
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 W_1 U_2 V_2 W_2 \vdots U_M V_M W_M
出力
答えを出力せよ。
入力例 1
3 3 1 2 3 2 3 5 1 3 4
出力例 1
22
町 1 から町 2 へ水を流すとき、 町 1 から町 2 への水道管で水を 3 流すことができ、町 1 から 町 3 を経由して町 2 へ水を 4 流すことができます。また、このときが流せる最大の水の量を達成しています。よって、f(1,2)=3+4=7 です。
P=(3,1,2) の時f(1,3)+f(2,1)+f(3,2)=7+7+8=22 です。また、どのような P でも f(1,P_1)+f(2,P_2)+f(3,P_3) が 23 以上になることはないため求めるべき答えは 22 です。
入力例 2
5 10 1 3 36426 4 3 90081 3 5 3497 2 1 68417 5 1 35902 2 4 23857 5 2 29211 3 2 63340 5 4 60016 1 4 24593
出力例 2
820246