Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
高橋一二三君は、自分の本名に "123" がついていることから、面白いとクラスの人たちに笑われてしまいました。
それ以来、彼は "123" という整数が嫌いになりました。
そのため、高橋君が「1, 2, 3, 4, ...」と整数を順に言うときには、必ず 123 を飛ばして数えます。
彼が 1 から N まで整数を順に言うとき、何個の整数を言うでしょうか。
制約
- N は 123 ではない 1 以上 1 \ 000 以下の整数
入力
入力は以下の形式で標準入力から与えられます。
N
出力
彼は何個の数を言うか、1 行に出力してください。
最後に改行をしてください。
小課題
小課題 1 [40 点]
- N \leq 10 を満たす。
小課題 3 [60 点]
- 追加の制約はない。
入力例 1
10
出力例 1
10
N = 10 の場合、普通どおり 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 と数を言います。
ですので、高橋君は 10 個の数を言います。
入力例 2
124
出力例 2
123
N = 124 の場合、1 → 2 → ... → 121 → 122 → 124 と数を言うため、合計で 123 個の数を言うことになります。
入力例 3
1000
出力例 3
999
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
パ研という部活には、N 人の部員がいます。それぞれの部員には、年齢順に 1, 2, 3, ..., N と番号が付けられています。
部員 i の競技プログラミングの実力は A_i です。
競技プログラミングではチーム戦が多くあります。パ研では、「チームの戦闘力」を、チームで最も実力が低い人の実力の値、と定義しました。
例えば、実力が 5, 4, 10 の人がいる 3 人チームの戦闘力は、4 となります。
ある日突然、2020 年に開催される東京オリンピックの種目に、「競技プログラミング」が追加されました。この大会には、ちょうど D 人で構成されるチームで出場しなければなりません。
パ研の部員全員が、代表選抜に応募したいです。その為、パ研はチーム分けを以下のような方法で行うことにしました。
- 出来るだけ多くの人が、代表選抜に応募できることにする。
- その中で、チームの戦闘力の合計 が最大になるようにチーム編成をする。
- ただし、同じ人が複数のチームに入ってはならない。
さて、チームの戦闘力の合計はいくつになるでしょうか?
制約
- N は 1 以上 1 \ 000 以下の整数
- D は 1 以上 10 以下の整数
- A_i は 1 以上 4 \ 208 以下の整数
- 全く同じ実力の部員はいない
入力
入力は以下の形式で標準入力から与えられます。
N D A_1 A_2 A_3 ... A_N
出力
問題文中の方法に従ってチーム編成をした時、チームの戦闘力の合計はいくつか、整数で一行に出力してください。
小課題
小課題 1 [25 点]
- N = D を満たす.
小課題 3 [75 点]
- 追加の制約はない.
入力例 1
4 2 20 18 12 24
出力例 1
32
部員の実力は、部員 1 から順に {20, 18, 12, 24} です。
チームを以下のように決めると、戦闘力の合計が 20 + 12 = 32 となります。
- 部員 1 と 4 で構成されるチーム: 戦闘力は min(20, 24) = 20
- 部員 2 と 3 で構成されるチーム: 戦闘力は min(18, 12) = 12
入力例 2
5 5 8 6 9 1 20
出力例 2
1
N = D なので、1 チームしか作れません。また、1 チーム編成するとき、過不足なくどの部員も代表選抜に参加できます。
そのため、戦闘力の合計は min(8, 6, 9, 1, 20) = 1 となります。
入力例 3
6 8 1268 1755 2315 1071 1229 1101
出力例 3
0
N < D なので、1 チームも作れません。そのため、戦闘力の合計は 0 となります。
入力例 4
8 3 1345 1355 1390 1285 1171 936 1272 855
出力例 4
2516
8 人から 3 人チーム 2 つを作るので、あぶれてしまう人がどうしても 2 人出てしまいます。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
クリスマスの飾りつけとして、N 個のオーナメントを一列に並べることにしました。
オーナメントの色(例えば、赤・青・金など)は N 種類あり、それぞれ番号が 1, 2, ..., N と付けられています。
左から i 個目のオーナメントは、番号 a_i の色の飾りつけにすることを決めました。ただし、まだ色が決まっていないオーナメントは、a_i = 0 として表されます。
あなたは、クリスマスの飾りつけの「周期」をできるだけ短くするようにしたいです。
クリスマス飾りの「周期」は、以下のように定義されます。
- 左から数えて最初の X 個のオーナメントの色が、その後も繰り返されている (ただし最後の部分が途切れていても良い) ような X の中で、最小の X が「周期」である。
- つまり、左から i 番目のオーナメントの色が p_i のとき、全ての i (1 \leq i \leq N-X) において p_i = p_{i+X} となっている X の中で最小の X が「周期」である。
- 例えば、p = (1, 3, 2, 1, 3, 2, 1, 3) の場合「周期」 = 3、p = (1, 3, 5, 5, 5, 1, 3, 5, 5) の場合「周期」 = 5 である。また、全ての色が同じ場合、「周期」 = 1 である。
「周期」が最小になるようにまだ決まっていないオーナメントの色を決めた時、「周期」の値はいくつになるか求めてください。
制約
- N は 1 以上 2 \ 019 以下の整数
- 0 \leq a_i \leq N
入力
入力は以下の形式で標準入力から与えられます。
N a_1 a_2 a_3 ... a_N
出力
飾りつけの「周期」として考えられる最小の値を、一行で出力してください。
小課題
小課題 1 [10 点]
- N \leq 3 を満たす。
小課題 2 [30 点]
- a_i \neq 0 を満たす。
小課題 3 [30 点]
- N \leq 50 を満たす。
小課題 4 [30 点]
- 追加の制約はない。
入力例 1
11 1 2 3 0 2 3 1 0 3 1 0
出力例 1
3
クリスマス飾りの 4 番目、8 番目、11 番目の飾りつけの色はまだ決まっていません。それらの色の番号をそれぞれ 1, 2, 2 にすると、以下のような飾りつけになります。
(1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2)
これは、周期が 3 となります。これ以下の周期となるような色の決め方はないので、3 が答えとなります。
入力例 2
3 2 2 3
出力例 2
3
全ての色が決まっており、この飾りつけの周期は 3 となります。
また、この入力例は小課題 1, 2 両方の制約を満たします。
入力例 3
13 12 2 0 0 2 0 0 2 4 12 0 4 0
出力例 3
3
飾りつけの色の番号 (12, 2, 4, 12, 2, 4, 12, 2, 4, 12, 2, 4, 12) にすると、周期が 3 になります。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
N 個のオセロの駒が左から右に一直線に並べられています。
駒の色は文字列 S で表され、S の左から i 文字目が左から i 番目の駒に対応しており、W のとき白、B のとき黒が表になっていることを表します。
マジシャンの IOI 君は、駒を M 個新たに置きました。i 個目の駒の置き方は、D_i, F_i の 2 つの値で決まり、
- D_i =
Lのとき一番左の駒の少し左に置き、D_i =Rのとき一番右の駒の少し右に置くことを表し、 - F_i =
Wのとき表を白、F_i =Bのとき表を黒にして駒を置くことを表す。 - 駒を置いた瞬間。置いた石と、それに最も近い同じ色の別の石に挟まれた石はすべて裏返されます!
しかし、JOI 君はこの手品を見ることができませんでした。そこで、手品の内容がどのようなものだったか知るために、Q 個の質問をしました。 i 個目の質問は、「T_i 回目に駒を置いたとき、(その時点での) 左から P_i 番目の駒の色が何だったか?」です。
IOI 君のために、その質問すべてに答えてください。
制約
- N は 1 以上 150 \ 000 以下の整数
- M は 1 以上 150 \ 000 以下の整数
- Q は 1 以上 150 \ 000 以下の整数
- S は長さ N の
WとBだけで構成された文字列である - D_i は
LまたはR - F_i は
WまたはB - T_i は 1 以上 M 以下
- T_i 回目に駒を置き終わったとき、駒は P_i 個以上ある
- D_i, F_i, S 以外の入力は全て整数
入力
入力は以下の形式で標準入力から与えられます。
N S M D_1 F_1 D_2 F_2 : : D_M F_M Q T_1 P_1 T_2 P_2 : : T_Q P_Q
出力
Q 行にわたって出力してください。
i 行目には、i 回目の質問の答えを出力してください。
小課題
小課題 1 [25 点]
- N \leq 100 を満たす。
- M \leq 100 を満たす。
- Q \leq 100 を満たす。
小課題 2 [29 点]
- N = 1 を満たす。
小課題 3 [33 点]
- N \leq 100 を満たす。
小課題 4 [13 点]
- 追加の制約はない。
入力例 1
5 WWBBW 3 L B R W R B 2 1 2 3 4
出力例 1
B B
最初、駒の色は WWBBW となっています。
1 回目、左に B を置くと、BWWBBW → BBBBBW となります。一番左の B と次の (左から 4 番目の) B に挟まれた駒はすべてひっくり返されるからです。
2 回目、右に W と置くと、BBBBBWW となるが、その後何も裏返されません。
3 回目、右に B と置くと、BBBBBWWB → BBBBBBBB となります。
次に、JOI 君の質問に答えます。
1 個目の質問は、「1 回目が終わった後に、左から 2 つ目はどちらが表を向いていたか?」です。1 回目が終わった後は BBBBBW なので、左から 2 つ目は B、すなわち黒色です。
2 個目の質問は、「3 回目が終わった後に、左から 4 つ目はどちらが表を向いていたか?」です。3 回目が終わった後は BBBBBBBB なので、左から 4 つ目は B、すなわち黒色です。
入力例 2
1 B 5 L W L B R W R W L W 5 1 1 2 2 3 2 4 5 5 3
出力例 2
W B B W W
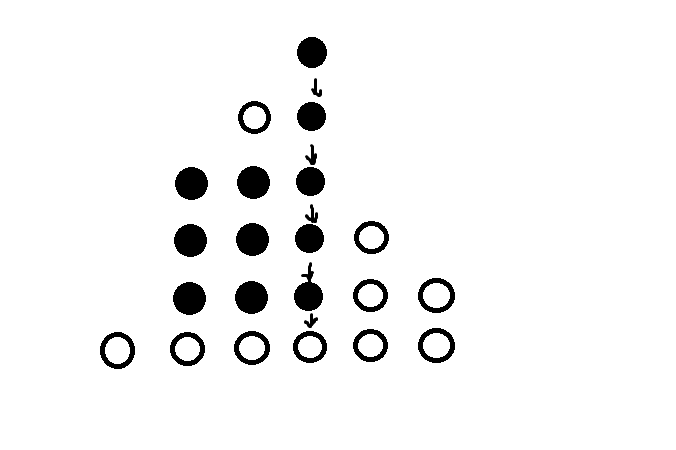
最初、駒は B となっていくが、WB → BBB → BBBW → BBBWW → WWWWWW と変化していきます。
つまり、この入力例において、以下のようにオセロの並びは変化します。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
今日はクリスマス・イブである。PAKEN 君は、平成最後のクリスマスに向けて、以下のようなデコレーションを作りました。
- デコレーションは、「電球」と「棒」で構成される。デコレーションは、以下のようにして作られる。
- 電球 (a, b) (0 \leq a \leq D, -a \leq b \leq a) を満たす整数の組) を作る。a を「深さ」と呼び、b を「横座標」と呼ぶ。
- 電球 (0, 0) と (1, -1) を、そして電球 (0, 0) と (1, 1) を、直接棒で結ぶ。
- 同じ深さで横座標が 1 しか違わない電球同士を、直接棒で結ぶ。
- 電球 (a, -(a-1)) と (a+1, -(a+1)) を、そして電球 (a, a-1) と (a+1, a+1) を、直接棒で結ぶ。
例えば、D = 1, 2, 3 のとき、グラフは以下の図のようになります。
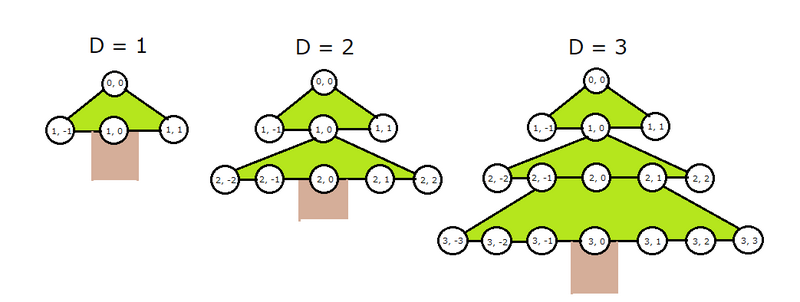
どうやらクリスマスツリーみたいな感じです。
PAKEN 君は、色 1 から X までの X 個の色を使って、全ての電球に色を付けたいです。ただし、棒で直接結ばれた電球は同じ色であってはいけません。
色の付け方は何通りあるか、1 \ 000 \ 000 \ 007 で割った余りを求めてください。
制約
- D は 1 以上 10 \ 000 \ 000 以下の整数
- X は 1 以上 1 \ 000 \ 000 \ 000 以下の整数
入力
入力は以下の形式で標準入力から与えられます。
D X
出力
色の付け方は何通りあるか、1 \ 000 \ 000 \ 007 で割った余りを一行に出力してください。
小課題
小課題 1 [2 点]
入力は以下の条件を満たす。
- D = 1
- X \leq 4
小課題 2 [12 点]
入力は以下の条件を満たす。
- D \leq 2
- X \leq 6
小課題 3 [21 点]
入力は以下の条件を満たす。
- D \leq 4
- X \leq 7
小課題 4 [31 点]
入力は以下の条件を満たす。
- D \leq 50
- X \leq 25
小課題 5 [18 点]
- D \leq 50 を満たす。
小課題 6 [11 点]
- D \leq 100 \ 000 を満たす。
小課題 7 [5 点]
- 追加の制約はない。
入力例 1
1 2
出力例 1
2
以下の 2 通りの塗り方が存在します。

入力例 2
1 3
出力例 2
18
以下の 18 通りの塗り方が存在します。

この入力は、小課題 1 の制約を満たします。
入力例 3
4 5
出力例 3
101969466
この入力は、小課題 2 の制約は満たしませんが、小課題 3 の制約を満たします。
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
PAKEN 市長の E869120 氏は、市にいくつかのチェックポイントと、2 つのチェックポイントを結ぶいくつかの一方通行の道路を建設することを計画しました。
チェックポイントの数を N とし、チェックポイントを 1, 2, 3, ..., N と番号付けするものとします。
太古の時代から、この市のラッキーナンバーは K とされています。
そのため、市長は以下のような条件を満たすものを建設することに決めました。
- チェックポイント 1 から N まで行く方法の通り数が、ちょうど K 通りである。
- チェックポイント 1 から N まで行く方法のうち、どの経路を選んで通っても、通る道路の本数は変わらない。
例えば、K = 5 のとき、以下のチェックポイントと道路の配置は条件を満たします。何故なら、チェックポイント 1 から N まで行く方法の総数は K = 5 通りであり、全ての行き方についてちょうど 3 本の道を通るからです。

コストの関係上、市長はできるだけチェックポイントの数 N をできるだけ小さくしたいです。
このような条件を建設の仕方を 1 つ構成してください。ただし、チェックポイント a から b まで直接行く道路は a < b でないと建てられず、複数の「同じ 2 つのチェックポイントを結ぶ道路」を建ててはいけないものとします。
制約
- K は 1 以上 10^{18} 以下の整数
入力
入力は以下の形式で標準入力から与えられる。
K
出力
出力は以下の形式で行うこと。
N M a_1 b_1 a_2 b_2 a_3 b_3 ... a_M b_M
- 1 行目には、チェックポイントの数 N と、道路の数 M を空白区切りで出力してください。
- 2 行目から M 行にわたって、道の情報を出力してください。ただし、a_i, b_i は、「i 番目の道路がチェックポイント a_i から b_i へ直接結ぶ」ことを表します。このとき a_i < b_i でなければなりません。
- 最後に改行をしてください。
ただし、N は 200 以下でなければなりません。 そうでない場合、Wrong Answer となります。
また、(a_i, b_i) \neq (a_j, b_j) (i \neq j) かつ a_i < b_i でなければなりません。
小課題
小課題 1 [8 点]
- K \leq 150 を満たす。
小課題 2 [12 点]
- K \leq 8 \ 000 を満たす。
小課題 3 [80 点]
- 追加の制約はない。
ただし、小課題 3 について、採点は以下のように行われます。そこでは、L を「全てのテストケースにおける N の最大値」とします。
- 161 \leq L \leq 200 の場合、15 点
- 152 \leq L \leq 160 の場合、55 - (L - 150) * 2 点
- L = 151 の場合、65 点
- L \leq 150 の場合、80 点満点
なお、小課題 1, 2 においては N \leq 200 であれば正解と判定されます。
入力例 1
5
出力例 1
7 10 1 2 1 3 1 4 2 5 3 5 3 6 4 5 4 6 5 7 6 7
以下の図において、チェックポイント 1 から 7 まで行くのに 5 通りの方法が存在し、全て同じ本数 (3 本) の道路を通るため、条件を満たします。

入力例 2
20
出力例 2
16 24 1 2 2 3 3 4 5 6 6 7 7 8 9 10 10 11 11 12 13 14 14 15 15 16 1 5 5 9 9 13 2 6 6 10 10 14 3 7 7 11 11 15 4 8 8 12 12 16
以下の図において、チェックポイント 1 から 16 まで行くのに 20 通りの方法が存在し、全て同じ本数 (6 本) の道路を通るため、条件を満たします。

入力例 3
104
出力例 3
21 75 1 2 1 3 2 4 2 5 2 6 2 7 3 4 3 5 3 6 3 7 4 8 4 9 4 10 4 11 4 12 4 13 4 14 4 15 4 16 4 17 4 18 4 19 4 20 5 8 5 9 5 10 5 11 5 12 5 13 5 14 5 15 5 16 5 17 5 18 5 19 5 20 6 8 6 9 6 10 6 11 6 12 6 13 6 14 6 15 6 16 6 17 6 18 6 19 6 20 7 8 7 9 7 10 7 11 7 12 7 13 7 14 7 15 7 16 7 17 7 18 7 19 7 20 8 21 9 21 10 21 11 21 12 21 13 21 14 21 15 21 16 21 17 21 18 21 19 21 20 21
この入力は、小課題 1 の制約を満たします。
Time Limit: 1 sec / Memory Limit: 1024 MiB
配点: 100 点
リジャッジをしました。(18/12/24 16:07 JST)
問題文
パ研合宿の運営リーダーである E869120 氏は、N 頂点 M 辺の連結な無向グラフを持っています。i 番目の辺は、頂点 a_i と b_i を結んでいます。
12 月 24 日、今日はクリスマスイブです。
そのため、彼はグラフに色を付け、パ研部長である reiji1112 氏にプレゼントすることを計画しました。
しかし、辺で直接隣り合う頂点が同じ色だと見栄えが良くないので、辺で直接隣り合う頂点同士は違う色で塗る必要があります。
色は K 色準備されています。色 1, 2, 3, ..., K と番号付けられています。
さて、塗り方は何通りあるでしょうか? 1 \ 000 \ 000 \ 007 で割った余りを求めてください。
制約
- N は 1 以上 100 \ 000 以下の整数
- M は 1 以上 100 \ 003 以下の整数
- M - N は 3 以下である。
- K は 1 以上 1 \ 000 \ 000 \ 000 以下の整数
- a_i, b_i は 1 以上 N 以下の整数
- a_i < b_i (1 \leq i \leq M)
- (a_i, b_i) \neq (a_j, b_j) (i \neq j)
入力
入力は以下の形式で標準入力から与えられます。
N M K a_1 b_1 a_2 b_2 a_3 b_3 ... a_M b_M
出力
グラフの塗り方は何通りあるか、1 \ 000 \ 000 \ 007 で割った余りを求めてください。
小課題
小課題 1 [4 点]
入力は以下の条件を満たす。
- N \leq 8.
- K \leq 2.
小課題 2 [13 点]
- N \leq 8 を満たす。
小課題 3 [8 点]
- M - N = -1 かつ a_i = i, b_i = i + 1 (1 \leq i \leq M) を満たす。
小課題 4 [13 点]
- M - N \leq -1 を満たす。
小課題 5 [13 点]
- M - N \leq 0 を満たす。
小課題 6 [13 点]
- M - N \leq 1 を満たす。
小課題 7 [13 点]
- M - N \leq 2 を満たす。
小課題 8 [23 点]
- 追加の制約はない。
入力例 1
3 2 2 1 2 2 3
出力例 1
2
以下の 2 通りの塗り方が条件を満たします。

入力例 2
3 2 5 1 2 2 3
出力例 2
80
この入力例は小課題 1 の制約は満たしませんが、小課題 2 〜 8 の制約は満たします。
入力例 3
4 3 1 1 2 2 3 2 4
出力例 3
0
入力例 4
6 5 4 1 2 1 3 2 4 2 5 3 6
出力例 4
972
入力例 5
10 10 100 1 2 1 3 2 4 2 5 2 6 2 7 3 8 5 9 9 10 4 8
出力例 5
332858118
答えを 1 \ 000 \ 000 \ 007 で割った余りを求めてください。
Time Limit: 1 sec / Memory Limit: 1024 MiB
問題文
サンタクロースは、PAKEN CITY という街でプレゼントを配ります。
PAKEN CITY は (2N+1) \times (2N+1) のマス目で表される街で、北から i+1 マス目、西から j+1 マス目のマスを (i, j) で表します。
このとき、i を「行番号」、j を「列番号」ということにします。
PAKEN CITY の各マスは、「道路」「更地」「家」のいずれかです。
行番号と列番号のどちらかが偶数のマスはすべて道路であり、両方奇数のマスは更地または家です。
入力で与えられる S_{R, C} はマス (2R+1, 2C+1) に対応しており、. のとき「更地」であり、1〜9 のとき家であり、この数字は家に住む人数を表します。
サンタクロースの reiji1112 君は、ある道路の交差点 (行番号、列番号が両方偶数のマス) からスタートして、同じマスを 2 度通らずに K 個以下の交差点を通って元の場所に戻る経路をたどってプレゼントを配ります。 また、家に (4 方向に) 隣接するマスから、この家にプレゼントを配ることができます。1 つの家に配れるプレゼントは、この家に住む人数までです。また、同じ家に 2 回以上プレゼントを配ることはできません。
サンタクロースができるだけ多くのプレゼントを配れるような、移動経路を作ってください。
サンタの移動経路の例は、以下の入力の場合、次のようになります。
3 6 123 4.5 678

この場合、2 + 4 + 5 + 6 + 7 + 8 = 32 人に対してプレゼントを配ることができます。
入力
N K
S_{0,0}S_{0,1}S_{0,2}...S_{0,N-1}
S_{1,0}S_{1,1}S_{1,2}...S_{1,N-1}
S_{2,0}S_{2,1}S_{2,2}...S_{2,N-1}
: : :
S_{N-1,0}S_{N-1,1}S_{N-1,2}...S_{N-1,N-1}
出力
スタートする交差点の座標が (2R, 2C) とし、最初の位置から順に、「東、西、南、北方向に 2 マス進むとき、それぞれ R, L, D, U」をつなげた K 文字以下の文字列を X とするとき、各ケースに対して:
R C X
と出力してください。X の文字数はそのケースにおける K 文字以下にしてください。例えば、問題文中の図の例における出力は 1 1 DDRUUL となります。しかし、いくつかのケースの結果が得られていないときは、そのケースに対して代わりに:
-1 -1 -1
と出力してください。
全部で 6 ケースあるので、ケース 1 から順に 6 行で出力してください。
ただし、この問題は Output Only 形式で、入力データも与えられているので、手元の環境で答えを求める場合は Text(cat) 言語 (出力そのままの文字列) で提出することを推奨します。
1 1 DDRUUL -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
このように、6 行で出力してください。しかし、このような出力をしても 0 点となります。詳しくは、「得点」の項をご覧ください。
なお、スタートした場所に戻ってくる経路ではない場合や、$X$ が $K$ 文字を超えた場合、PAKEN CITY からはみ出るような経路を出力した場合、WA などのエラーが出ますのでご注意ください。
ケースについて
ケースは、次のようになっている。
| ケース番号 | 得点 | N | K | V_1 | V_2 | V_3 | V_4 | V_5 |
| #1 | 10 | 9 | 24 | 220 | 260 | 271 | - | - |
| #2 | 18 | 100 | 280 | 2766 | 2937 | 3051 | 3110 | 3230 |
| #3 | 18 | 500 | 1400 | 13299 | 14104 | 14641 | 14940 | 15820 |
| #4 | 18 | 500 | 1400 | 3346 | 3975 | 4394 | 4600 | 5060 |
| #5 | 18 | 500 | 1400 | 11368 | 15543 | 16198 | 16600 | 17490 |
| #6 | 18 | 100 | 1000 | 8950 | 9783 | 10338 | 10660 | 11310 |
入力データは、次の ZIP ファイル をダウンロードすることで入手できます。
得点
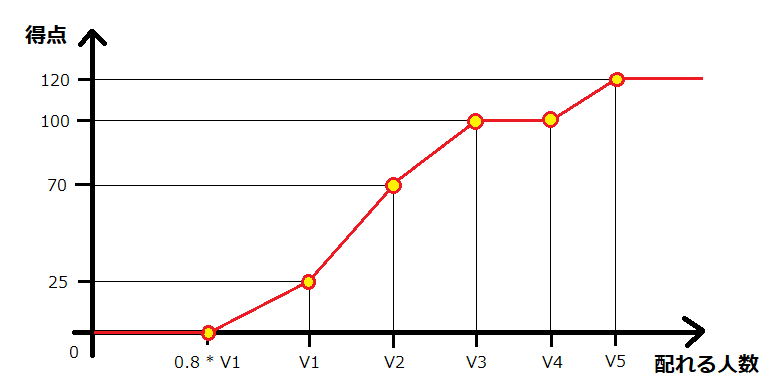
先ほどの「ケース」の部分で、V_1, V_2, V_3, V_4, V_5 という値が決まっていましたが、これは得点に関係します。
- まず、V_1 は 25 パーセント点のラインです。この 0.8 倍以下になると 0 点であり、0.8 倍〜1 倍のとき、点数は 1 次関数的に増えます。
- 次に、V_2 は 70 パーセント点のラインです。V_1 から V_2 の間も点数は 1 次関数的に増えます。
- 次に、V_3 は 100 パーセント点のラインです。V_2 から V_3 の間も点数は 1 次関数的に増えます。
- V_3 から V_4 まではすべで 100 パーセント点です。
- スコア V_4 を超えると、スコア V_5 まで点数が 1 次関数的に増え、V_5 のときに最大の点数 120 パーセント点になります。
すなわち、得点の変化は以下のグラフのようになります。