Time Limit: 2 sec / Memory Limit: 1024 MiB
ストーリー
第二回マスターズ選手権のオンサイト決勝大会が終了した。 大会会場には燃えるごみ、燃えないごみ、資源ごみの3種類のごみが散乱している。
高橋くんは燃えるごみを、青木くんは燃えないごみを、それぞれ担当して回収することになった。 2人はごみ袋を両手に広げ、会場内を歩き回りながらごみを回収していく。
ごみは正しく分別する必要があり、高橋くんは燃えるごみのみを、青木くんは燃えないごみのみを回収したい。 資源ごみは後で業者が回収するため、その場に残しておく。
できるだけ短い時間で、燃えるごみと燃えないごみをすべて回収してほしい。
問題文
10^6\times 10^6 の二次元平面上に、点として表される X 個の燃えるごみ、Y 個の燃えないごみ、Z 個の資源ごみが散乱している。 あなたは高橋くんと青木くんに指示を出し、それぞれすべての燃えるごみ・燃えないごみを回収させたい。
高橋くんと青木くんは、それぞれごみ袋の端を左右の手で持っており、ごみ袋の開口部は左右の手を結ぶ線分として表される。 左手の現在位置を p=(p_x, p_y)、右手の現在位置を q=(q_x, q_y) とし、1回の操作でそれぞれを p'=(p_x', p_y') および q'=(q_x', q_y') に直線的に移動させる。 このとき、2つの三角形 \triangle pqp' および \triangle p'qq' の内部およびその境界上にあるごみは、すべて回収され、平面上から取り除かれる。 この操作を繰り返すことで、ごみ袋を操作してごみを回収する。
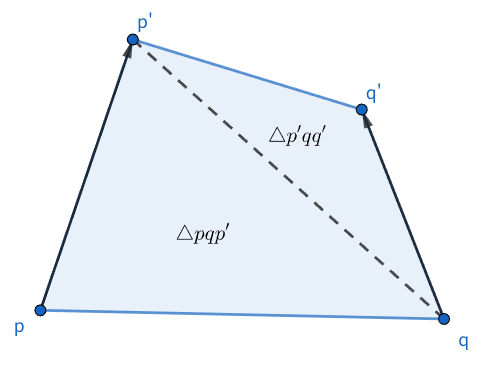
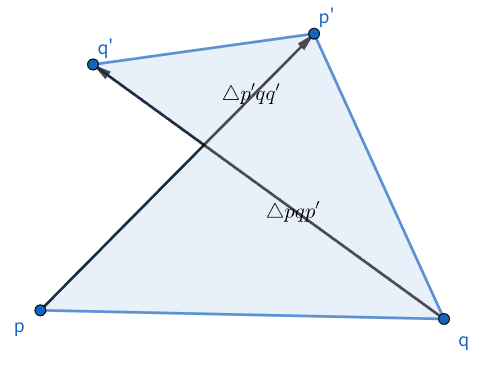
注意: 左右の手の動きが交差する場合に回収する領域が直感と異なるように見えるかもしれないが、この問題では簡単のため左手を先に動かしてから次に右手を動かしたものとして扱っている。
高橋くんと青木くんの計4本の手は同じ座標に重なってもかまわない。 両方の手を重ねて一緒に動かす場合など、三角形が線分に退化している場合、線分上のごみが回収される。
ヒント: 三角形に対する点の内外判定
三角形 \triangle abc の内部またはその境界上に、点 p が存在するかどうかは、たとえば以下の Python コードにより判定することができる。 ここでは、p[0] が x 座標、p[1] が y 座標を表す。 このコードは、三角形が線分や1点に退化している場合でも正しく動作し、さらにすべて整数演算で処理されるため、誤差なく判定が可能である。
def orient(a, b, p):
return (b[0] - a[0]) * (p[1] - a[1]) - (b[1] - a[1]) * (p[0] - a[0])
def contains(p, a, b, c):
# degenerate (colinear) case
if orient(a, b, c) == 0:
if orient(a, b, p) != 0 or orient(a, c, p) != 0:
return False
xs = (a[0], b[0], c[0])
ys = (a[1], b[1], c[1])
return min(xs) <= p[0] <= max(xs) and min(ys) <= p[1] <= max(ys)
# non‐degenerate: check same side of all edges
c1 = orient(a, b, p)
c2 = orient(b, c, p)
c3 = orient(c, a, p)
return (c1 >= 0 and c2 >= 0 and c3 >= 0) or (c1 <= 0 and c2 <= 0 and c3 <= 0)
ごみ袋は十分に大きく、また2人の腕も十分に長いため、左右の手がどれだけ離れていてもかまわない。 4本の手の初期位置は、それぞれ整数座標 (x, y) のうち、0 \leq x \leq 10^6,\ 0 \leq y \leq 10^6 を満たすものから自由に選択できる。 また、手の移動先の座標 (x, y) も、同様に 0 \leq x \leq 10^6,\ 0 \leq y \leq 10^6 を満たす整数でなければならない。
あなたの一回の指示で、高橋くんと青木くんは同時に両手を動かす。 このとき、2人の回収領域が重なってもかまわないが、その場合は高橋くんが先に領域内のごみを回収する。 左右の手の初期位置を結ぶ線分上にあるごみは最初の指示の際に回収される。
左右の手を動かすには、その移動距離の和の時間がかかる。 2人は常に同期して行動するため、一回の指示にかかる所要時間は、2人のうち所要時間が大きい方になる。
すなわち、 高橋くんの左手を p_1 から p_1' に、右手を q_1 から q_1' に、 青木くんの左手を p_2 から p_2' に、右手を q_2 から q_2' に動かす指示を出したとき、 その操作の完了にかかる時間は次の通りである:
\[ \max(\mathrm{dist}(p_1,p_1')+\mathrm{dist}(q_1,q_1'),\mathrm{dist}(p_2,p_2')+\mathrm{dist}(q_2,q_2')) \]
ここで、\mathrm{dist}(p, q) は2点 p, q 間のユークリッド距離を表す。
操作指示は、最大で 10000 回まで出すことができる。 次の条件をすべて満たすような操作方法のうち、合計所要時間ができるだけ短いものを求めてほしい。
- 高橋くんがすべての燃えるごみを回収する
- 青木くんがすべての燃えないごみを回収する
- 2人とも、資源ごみを一切回収しない
得点
高橋くんが回収した燃えるごみの個数を X'、青木くんが回収した燃えないごみの個数を Y'、回収されなかった資源ごみの個数を Z' とする。 合計時間を T としたとき、以下の得点が得られる。
- X'+Y'+Z'=X+Y+Z かつ T\leq 10^8 の場合、\mathrm{round}\left(10^6\times \left(1+\log_2 \frac{10^8}{T}\right)\right)
- X'+Y'+Z'\lt X+Y+Z もしくは T>10^8 の場合、\mathrm{round}\left(10^6\times \frac{X'+Y'+Z'}{X+Y+Z}\right)
入力生成方法の違いにより、問題は A・B・C の 3 問 に分かれている。 各問題にはそれぞれ 150 個のテストケース があり、各テストケースの得点の合計がその問題に対する提出の得点となる。 一つ以上のテストケースで不正な出力や制限時間超過をした場合、提出全体の判定がWAやTLEとなる。 各問題に対して獲得した最高得点の総和で最終順位が決定され、コンテスト終了後のシステムテストは行われない。 同じ得点を複数のチームが得た場合、提出時刻に関わらず同じ順位となる。
入力
入力は以下の形式で標準入力から与えられる。
X Y Z
x_0 y_0
\vdots
x_{X+Y+Z-1} y_{X+Y+Z-1}
- 燃えるごみの個数 X は X=100 で固定されている。
- 燃えないごみの個数 Y は Y = 0 または Y = 100 のいずれかである。
- 資源ごみの個数 Z は 0\leq Z\leq 100 を満たす。
- ごみの座標は整数 (x_i, y_i) で与えられ、すべての座標は 1 \leq x_i, y_i \leq 10^6 - 1 を満たす。
- ごみの種別とインデックスの対応は次の通り:
- i = 0, \dots, X - 1:燃えるごみ
- i = X, \dots, X + Y - 1:燃えないごみ
- i = X + Y, \dots, X + Y + Z - 1:資源ごみ
- 任意の2つのごみの間のユークリッド距離は、10^3 以上離れていることが保証される。
- 以下の4つの条件のそれぞれを満たすような燃えるごみ (x,y) が、少なくとも1つずつ存在する。これにより、燃えるごみをすべて回収するには、少なくとも T\geq 2\times 10^5 の時間が必要なことが保証される。
- x\leq 4\times 10^5 かつ y\leq 4\times 10^5
- x\leq 4\times 10^5 かつ y\geq 6\times 10^5
- x\geq 6\times 10^5 かつ y\leq 4\times 10^5
- x\geq 6\times 10^5 かつ y\geq 6\times 10^5
出力
高橋くんの左右の手の初期位置をそれぞれ (x_{0,0},y_{0,0})、(x_{0,1},y_{0,1})、青木くんの左右の手の初期位置をそれぞれ (x_{0,2},y_{0,2})、(x_{0,3},y_{0,3}) とする。 操作回数を K とし、 t 回目の操作 (t=1,2,\cdots, K) では、高橋くんの左右の手の移動先を (x_{t,0},y_{t,0})、(x_{t,1},y_{t,1})、青木くんの左右の手の移動先を (x_{t,2},y_{t,2})、(x_{t,3},y_{t,3}) とする。
このとき、以下の形式で標準出力に出力せよ。
x_{0,0} y_{0,0} x_{0,1} y_{0,1} x_{0,2} y_{0,2} x_{0,3} y_{0,3}
\vdots
x_{K,0} y_{K,0} x_{K,1} y_{K,1} x_{K,2} y_{K,2} x_{K,3} y_{K,3}
なお、入力によっては燃えないごみが存在せず、青木くんの作業が不要な場合がある。 その場合には、たとえば x_{t,2}=y_{t,2}=x_{t,3}=y_{t,3}=0 と出力し、青木くんを隅で待機させておけば良い。
入力生成方法
- \mathrm{rand}(L,U): L 以上 U 以下の整数値を一様ランダムに生成する。
- \mathrm{rand\_double}(L,U): L 以上 U 以下の実数値を一様ランダムに生成する。
- \mathrm{normal}(\sigma): 平均 0、標準偏差 \sigma の正規分布からランダムに実数値を生成する。
各問題における、燃えないごみの個数 Y および資源ごみの個数 Z の範囲は、以下の表の通りである。
| 問題 | Y | Z |
|---|---|---|
| A | 0 | 10 から 100 |
| B | 100 | 0 |
| C | 100 | 1 から 100 |
ごみは、燃えるごみ → 燃えないごみ → 資源ごみ の順に、各種類について以下の手順で座標を生成する。
- ごみの個数 N を、指定範囲内から一様ランダムに決定する。
- クラスタ数 n を、\mathrm{rand}(5,10) により決定する。
- 各クラスタ i = 1, \dots, n に対し、以下のパラメータを生成する:
- 重み w_i=\mathrm{rand\_double}(0,1)
- 中心座標 cx_i,cy_i=\mathrm{rand}(200000,800000)
- 標準偏差 \sigma_{x,i},\sigma_{y,i}=\mathrm{rand}(30000,90000)
- 傾き \theta_i=\mathrm{rand\_double}(0,\pi)
- 以下の処理を N 回繰り返して、ごみの座標 (x, y) を N 個生成する:
- 重みに比例した確率でクラスタ i を選ぶ。
- x' = \mathrm{normal}(\sigma_{x,i})、y' = \mathrm{normal}(\sigma_{y,i}) を生成する。
- 座標 (x, y) を以下の式で計算する: \[ x=\mathrm{round}(cx_i+\cos(\theta_i)\cdot x'-\sin(\theta_i)\cdot y')\\ y=\mathrm{round}(cy_i+\sin(\theta_i)\cdot x'+\cos(\theta_i)\cdot y') \]
- (x, y) が 1 \leq x, y \leq 10^6 - 1 を満たし、かつこれまでに生成されたどのごみともユークリッド距離が 10^3 以上離れている場合、その座標を採用する。条件を満たさない場合は座標の再生成を行う。
ごみの種類が「燃えるごみ」の場合には、以下の4つの領域それぞれに該当するごみが少なくとも1つずつ存在することを確認する:
- x\leq 4\times 10^5 かつ y\leq 4\times 10^5
- x\leq 4\times 10^5 かつ y\geq 6\times 10^5
- x\geq 6\times 10^5 かつ y\leq 4\times 10^5
- x\geq 6\times 10^5 かつ y\geq 6\times 10^5
存在しない場合、クラスタ数の生成のステップからやり直す。
C問題について
C問題の入力は、各チームが自ら作成して提出によって差し替えることができる。 作成した入力の提出方法については、D問題のページを参照せよ。
各チームは4つの入力を提出する。提出された4つの入力のうち、ランダムに1件が全チームに公開され、残りの3件がジャッジに使用される。 入力の公開およびジャッジの開始は、コンテスト開始から3時間30分後を目安としている。 準備が整い次第、全体アナウンスを行う。
入力を提出しなかったチームの分は、前述の入力生成方法に従ってランダムに生成された4つの入力が代わりに用いられる。
なお、自分のチームが提出した入力は既知であるため、対応する出力を事前に計算して解答プログラムに埋め込むことも許される。
D問題への提出は何度でも行うことができる。ただし、各チームについて、コンテスト開始から 180 分未満 に提出されたもので ACを獲得した提出のうち、最後の1件のみが使用される。
ツール(入力ジェネレータ・スコア計算)
- ローカル版: 使用するにはRust言語のコンパイル環境をご用意下さい。
- Windows用のコンパイル済みバイナリ: Rust言語の環境構築が面倒な方は代わりにこちらをご利用下さい。
コンテスト期間中に、チーム外とのビジュアライズ結果の共有や解法・考察に関する言及は禁止されています。ご注意下さい。
Story
The on-site finals of the 2nd Masters Championship have just concluded. At the venue, three types of trash—burnable trash, non-burnable trash, and recyclable trash—are scattered across the floor.
Takahashi is assigned to collect burnable trash, and Aoki is assigned to collect non-burnable trash. Each of them holds a trash bag open with both hands and walks around the venue to collect trash.
Proper sorting of trash is required: Takahashi should collect only burnable trash, and Aoki should collect only non-burnable trash. Recyclable trash will be collected later by a professional service, so it should be left in place.
Your task is to help them collect all burnable and non-burnable trash in as little time as possible.
Problem Statement
On a two-dimensional plane of size 10^6 \times 10^6, there are X burnable trash items, Y non-burnable trash items, and Z recyclable trash items, each represented as a point. You are to instruct Takahashi and Aoki so that they collect all burnable and non-burnable trash respectively.
Takahashi and Aoki each hold the ends of a trash bag with their left and right hands, and the opening of the bag is represented by a line segment connecting their two hands. Let the current positions of the left and right hands be p = (p_x, p_y) and q = (q_x, q_y), respectively. In one operation, the hands can be moved in a straight line to new positions p' = (p_x', p_y') and q' = (q_x', q_y').
At this time, all trash located on or inside the two triangles \triangle pqp' and \triangle p'qq' is collected and removed from the plane. By repeating this operation, the trash bag can be moved to collect trash.


Note: When the movements of the left and right hands cross over, the collected area may appear counterintuitive. However, in this problem, for simplicity, the operation is treated as if the left hand moves first, followed by the right hand.
The four hands of Takahashi and Aoki are allowed to overlap at the same coordinates. When the triangle degenerates into a line segment, such as when both hands move together along the same path, trash located on the line segment is collected.
Hint: Point-in-triangle test
Whether a point p lies inside or on the boundary of a triangle \triangle abc can be determined using the following Python code as an example. Here, p[0] and p[1] represent the x- and y-coordinates of the point p, respectively. This code works correctly even when the triangle degenerates into a line segment or a single point, and since it uses only integer arithmetic, it allows for exact evaluation without rounding errors.
def orient(a, b, p):
return (b[0] - a[0]) * (p[1] - a[1]) - (b[1] - a[1]) * (p[0] - a[0])
def contains(p, a, b, c):
# degenerate (colinear) case
if orient(a, b, c) == 0:
if orient(a, b, p) != 0 or orient(a, c, p) != 0:
return False
xs = (a[0], b[0], c[0])
ys = (a[1], b[1], c[1])
return min(xs) <= p[0] <= max(xs) and min(ys) <= p[1] <= max(ys)
# non‐degenerate: check same side of all edges
c1 = orient(a, b, p)
c2 = orient(b, c, p)
c3 = orient(c, a, p)
return (c1 >= 0 and c2 >= 0 and c3 >= 0) or (c1 <= 0 and c2 <= 0 and c3 <= 0)
The trash bag is sufficiently large, and the arms of both Takahashi and Aoki are sufficiently long, so the left and right hands may be arbitrarily far apart. The initial positions of the four hands can be freely chosen from integer coordinates (x, y) that satisfy 0 \leq x \leq 10^6,\ 0 \leq y \leq 10^6. Likewise, the destination coordinates (x, y) for each hand must also be integers that satisfy the same condition.
In each instruction you give, both Takahashi and Aoki move both of their hands simultaneously. If their collection regions overlap, that is allowed—but in such cases, Takahashi collects the trash in the overlapping area first. Any trash located on the line segment connecting the initial positions of the left and right hands is collected during the first operation.
The time required to move both hands is the sum of their movement distances. Since Takahashi and Aoki always act in sync, the time taken for one instruction is the larger of the two individual times.
Specifically, when you instruct Takahashi to move his hands from p_1 to p_1' and from q_1 to q_1', and Aoki to move his hands from p_2 to p_2' and from q_2 to q_2', the time taken for the operation is:
\[ \max(\mathrm{dist}(p_1, p_1') + \mathrm{dist}(q_1, q_1'),\ \mathrm{dist}(p_2, p_2') + \mathrm{dist}(q_2, q_2')) \]
Here, \mathrm{dist}(p, q) denotes the Euclidean distance between points p and q.
You may issue at most 10000 instructions.
Your goal is to find a sequence of instructions that satisfies all of the following conditions, with as small total time as possible:
- Takahashi collects all burnable trash.
- Aoki collects all non-burnable trash.
- Neither of them collects any recyclable trash.
Scoring
Let X' be the number of burnable trash items collected by Takahashi, Y' be the number of non-burnable trash items collected by Aoki, and Z' be the number of recyclable trash items that remain uncollected. Let T be the total time.
The score is calculated as follows:
-
If X' + Y' + Z' = X + Y + Z and T \leq 10^8, then \mathrm{round}\left(10^6 \times \left(1 + \log_2 \frac{10^8}{T} \right)\right)
-
If X' + Y' + Z' < X + Y + Z or T > 10^8, then \mathrm{round}\left(10^6 \times \frac{X' + Y' + Z'}{X + Y + Z} \right)
The problem is divided into three subproblems: A, B, and C, based on different input generation methods. Each subproblem contains 150 test cases, and the total score for a submission to that subproblem is the sum of the scores from all test cases in it. If your submission produces an illegal output or exceeds the time limit for some test cases, the submission itself will be judged as WA or TLE , and the score of the submission will be zero.
The final ranking is determined by the sum of the highest scores obtained for each subproblem, and there will be no system test after the contest. If more than one team gets the same score, they will be ranked in the same place regardless of the submission time.
Input
Input is given from Standard Input in the following format:
X Y Z
x_0 y_0
\vdots
x_{X+Y+Z-1} y_{X+Y+Z-1}
- The number of burnable trash items X is fixed at X = 100.
- The number of non-burnable trash items Y is either Y = 0 or Y = 100.
- The number of recyclable trash items Z satisfies 0 \leq Z \leq 100.
- Trash coordinates are given as integer pairs (x_i, y_i), where all values satisfy 1 \leq x_i, y_i \leq 10^6 - 1.
- The correspondence between index i and trash type is as follows:
- i = 0, \dots, X - 1: burnable trash
- i = X, \dots, X + Y - 1: non-burnable trash
- i = X + Y, \dots, X + Y + Z - 1: recyclable trash
- The Euclidean distance between any two trash items is guaranteed to be at least 10^3.
- For each of the following four conditions, there exists at least one burnable trash item (x, y) that satisfies it.
This ensures that collecting all burnable trash requires at least T \geq 2 \times 10^5 time.
- x \leq 4 \times 10^5 and y \leq 4 \times 10^5
- x \leq 4 \times 10^5 and y \geq 6 \times 10^5
- x \geq 6 \times 10^5 and y \leq 4 \times 10^5
- x \geq 6 \times 10^5 and y \geq 6 \times 10^5
Output
Let Takahashi's initial left and right hand positions be (x_{0,0}, y_{0,0}) and (x_{0,1}, y_{0,1}), respectively, and Aoki's initial left and right hand positions be (x_{0,2}, y_{0,2}) and (x_{0,3}, y_{0,3}), respectively.
Let K be the number of operations. In the t-th operation (t = 1, 2, \dots, K), Takahashi's left and right hands move to (x_{t,0}, y_{t,0}) and (x_{t,1}, y_{t,1}), respectively, and Aoki's left and right hands move to (x_{t,2}, y_{t,2}) and (x_{t,3}, y_{t,3}), respectively.
Then, output to Standard Output in the following format.
x_{0,0} y_{0,0} x_{0,1} y_{0,1} x_{0,2} y_{0,2} x_{0,3} y_{0,3}
\vdots
x_{K,0} y_{K,0} x_{K,1} y_{K,1} x_{K,2} y_{K,2} x_{K,3} y_{K,3}
In some inputs, there may be no non-burnable trash, in which case Aoki has no tasks to perform. In such cases, for example, you may output x_{t,2} = y_{t,2} = x_{t,3} = y_{t,3} = 0 to have Aoki wait in a corner.
Input Generation
- \mathrm{rand}(L, U): Generates a random integer uniformly distributed between L and U (inclusive).
- \mathrm{rand\_double}(L, U): Generates a random real number uniformly distributed between L and U.
- \mathrm{normal}(\mu, \sigma): Generates a random real number from a normal distribution with mean \mu and standard deviation \sigma.
The ranges of the number of non-burnable trash items Y and recyclable trash items Z for each problem are as follows:
| Problem | Y | Z |
|---|---|---|
| A | 0 | from 10 to 100 |
| B | 100 | 0 |
| C | 100 | from 1 to 100 |
Trash items are generated for each type—in the order of burnable trash → non-burnable trash → recyclable trash—according to the following procedure:
- Determine the number of trash items N uniformly at random from the specified range.
- Determine the number of clusters n using \mathrm{rand}(5,10).
- For each cluster i = 1, \dots, n, generate the following parameters:
- Weight: w_i = \mathrm{rand\_double}(0, 1)
- Center coordinates: cx_i, cy_i = \mathrm{rand}(200000, 800000)
- Standard deviations: \sigma_{x,i}, \sigma_{y,i} = \mathrm{rand}(30000, 90000)
- Rotation angle: \theta_i = \mathrm{rand\_double}(0, \pi)
- Repeat the following process N times to generate N trash positions (x, y):
- Choose a cluster i at random, with probability proportional to its weight w_i.
- Generate x' = \mathrm{normal}(\sigma_{x,i})、y' = \mathrm{normal}(\sigma_{y,i}).
- Compute the coordinates (x, y) as follows: \[ x=\mathrm{round}(cx_i+\cos(\theta_i)\cdot x'-\sin(\theta_i)\cdot y')\\ y=\mathrm{round}(cy_i+\sin(\theta_i)\cdot x'+\cos(\theta_i)\cdot y') \]
- Accept the coordinate (x, y) if it satisfies 1 \leq x, y \leq 10^6 - 1 and is at least 10^3 away (Euclidean distance) from any previously generated trash item. Otherwise, retry the generation of (x, y).
If the type of trash being generated is burnable trash, ensure that there is at least one item in each of the following four regions:
- x \leq 4 \times 10^5 and y \leq 4 \times 10^5
- x \leq 4 \times 10^5 and y \geq 6 \times 10^5
- x \geq 6 \times 10^5 and y \leq 4 \times 10^5
- x \geq 6 \times 10^5 and y \geq 6 \times 10^5
If this condition is not met, restart the process from the cluster generation step.
Regarding Problem C
For Problem C, each team may create their own inputs and overwrite the default ones by submitting them. Refer to the page for Problem D for instructions on how to submit your inputs.
Each team may submit four inputs. Among the four submitted inputs, one is randomly selected and made public to all teams, while the remaining three are used for judging.
The input publication and the start of judging are scheduled to take place approximately 3 hours and 30 minutes after the contest begins. An announcement will be made to all participants once the system is ready.
For any team that does not submit their own inputs, four inputs will be generated randomly according to the input generation procedure described earlier.
Since each team knows the contents of the inputs they submitted, it is allowed to precompute the corresponding outputs and embed them into the solution program.
Submissions to Problem D may be made as many times as desired. However, for each team, only the last submission made within 180 minutes from the start of the contest that receives AC will be used for judging.
Tools (Input generator and score calculation)
- Local version: You need a compilation environment of Rust language.
- Pre-compiled binary for Windows: If you are not familiar with the Rust language environment, please use this instead.
Please be aware that sharing visualization results or discussing solutions/ideas outside of the team during the contest is prohibited.
Time Limit: 2 sec / Memory Limit: 1024 MiB
Time Limit: 2 sec / Memory Limit: 1024 MiB
この問題はA問題と同じで入力のみ異なります。 詳細はA問題を参照下さい。
この問題は、コンテスト開始から 3 時間 30 分後 を目安に解答可能となります。提出が可能になった時点で、全体アナウンスを行います。
This problem is the same as Problem A, differing only in input. See Problem A for details.
This problem will become available for solving approximately 3 hours and 30 minutes after the contest starts. An announcement will be made to all participants when submissions are allowed.