Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
ビ太郎は N 枚のカードを持っていて,カードには 1 から N までの番号が付けられている.各カードには 1 つの正の整数が書かれており,カード i (1 \leqq i \leqq N) に書かれた整数は A_i である.
以下の条件を満たす K 枚のカードの組を ストレート と呼ぶ.
- 書かれた整数が昇順になるように K 枚のカードを横一列に机に置いたとき,隣り合う 2 枚のカードに書かれた整数の差はすべて 1 である.
ビ太郎は N 枚のカードの中から,ストレートとなるような K 枚のカードを選びたい.
カードの情報が与えられたとき,ビ太郎がストレートとなるような K 枚のカードを選べるかどうか判定するプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
N K A_1 A_2 \cdots A_N
出力
標準出力に 1 行出力せよ.
ビ太郎がストレートとなるような K 枚のカードを選べる場合は Yes を,そうでない場合は No を出力せよ.
制約
- 2 \leqq N \leqq 300\,000.
- 2 \leqq K \leqq N.
- 1 \leqq A_i \leqq 10^9 (1 \leqq i \leqq N).
- 入力される値はすべて整数である.
小課題
- (30 点) K = 2.
- (30 点) A_i \leqq 300\,000 (1 \leqq i \leqq N).
- (40 点) 追加の制約はない.
入力例 1
5 2 1 1 2 4 3
出力例 1
Yes
カード 1, 3 に書かれた整数はそれぞれ 1, 2 であるから,カード 1, 3 の組はストレートである.
ビ太郎はストレートとなるような K = 2 枚のカードを選ぶことができるので,Yes を出力する.
この入力例はすべての小課題の制約を満たす.
入力例 2
7 4 1 1 2 3 3 5 6
出力例 2
No
ビ太郎はストレートとなるような K = 4 枚のカードを選ぶことができない.したがって,No を出力する.
この入力例は小課題 2, 3 の制約を満たす.
Time Limit: 1 sec / Memory Limit: 1024 MiB
配点: 100 点
葵さんは雪遊びをしている. 葵さんの目の前には N 個の雪玉が一直線上に並んでおり, 左から i 番目 (1 \leqq i \leqq N) の雪玉の大きさは A_i である.
葵さんは,最終的に大きな 1 つの雪玉を作りたいと考えている. そのために,以下の一連の操作を雪玉が 1 つになるか操作ができなくなるまで繰り返すことにした.
- 隣接する 2 つの雪玉を選ぶ.このとき,左側の雪玉の大きさを l,右側の雪玉の大きさを r とすると,0 \leqq l-r \leqq 1 でなければならない.
- 選んだ 2 つの雪玉を合成する.その結果,選んだ 2 つの雪玉は大きさ l+r の雪玉 1 つに置き換えられる.つまり,操作を行う前に左から大きさ s_1,s_2,\ldots,s_k の k 個の雪玉が並んでいるとき,左から t 番目 (1 \leqq t \leqq k-1) の雪玉と t+1 番目の雪玉を合成すると,操作後には左から大きさ s_1,s_2,\ldots,s_{t-1},s_t+s_{t+1},s_{t+2},\ldots,s_k の k-1 個の雪玉が並ぶ.
並んでいる雪玉の情報が与えられたとき,葵さんが適切に操作を行うことで雪玉を 1 つにすることができるか判定するプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
N A_1 A_2 \cdots A_N
出力
標準出力に 1 行出力せよ.
葵さんが雪玉を 1 つにすることができるなら Yes を,そうでないなら No を出力せよ.
制約
- 2 \leqq N \leqq 500\,000.
- 1 \leqq A_i \leqq 10^{12} (1 \leqq i \leqq N).
- 入力される値はすべて整数である.
小課題
- (15 点) A_1 = A_2 = \cdots = A_N.
- (18 点) N \leqq 8.
- (18 点) N \leqq 200.
- (19 点) N \leqq 5\,000.
- (30 点) 追加の制約はない.
入力例 1
5 1 1 1 1 1
出力例 1
Yes
例えば, 葵さんは次のように操作を行うことで最終的に雪玉を 1 つにすることができる.
- 左から 4 番目と 5 番目の雪玉を選択し,合成する.操作後には左から大きさ 1,1,1,2 の雪玉が並ぶ.
- 左から 1 番目と 2 番目の雪玉を選択し,合成する.操作後には左から大きさ 2,1,2 の雪玉が並ぶ.
- 左から 1 番目と 2 番目の雪玉を選択し,合成する.操作後には左から大きさ 3,2 の雪玉が並ぶ.
- 左から 1 番目と 2 番目の雪玉を選択し,合成する.操作後には左から大きさ 5 の雪玉が並ぶ.
この入力例はすべての小課題の制約を満たす.
入力例 2
3 2 2 2
出力例 2
No
葵さんがどのように操作を行っても雪玉を 1 つにすることはできない.
この入力例はすべての小課題の制約を満たす.
入力例 3
8 5 4 3 2 1 2 3 4
出力例 3
No
この入力例は小課題 2,3,4,5 の制約を満たす.
入力例 4
16 3 2 1 6 2 1 3 2 1 3 12 6 1 1 1 2
出力例 4
Yes
この入力例は小課題 3,4,5 の制約を満たす.
Time Limit: 5 sec / Memory Limit: 1024 MiB
配点: 100 点
IOI 王国は縦 L 行,横 L 列のマス目で表される領土を持っている.以降,上から i 行目 (1 \leqq i \leqq L),左から j 列目 (1 \leqq j \leqq L) のマスをマス (i, j) と表すことにする.
最近の IOI 王国では感染症で倒れる患者が相次いでおり,国民から医療の充実を求める声が上がっている.そこで,IOI 王国の国王であるビ太郎は,マス (1, 1),マス (1, L),マス (L, 1),マス (L, L) の 4 箇所に病院を建設し,それぞれの病院に 1 台ずつ救急車を設置することにした.
用心深いビ太郎は,実際に患者から救助要請があったときのことを想定してシミュレーションを行うことにした.ビ太郎が想定するシナリオでは,時刻 0 において N 人の患者から救助要請が届くので,時刻 T までにすべての患者をいずれかの病院に搬送することができるかどうかを調べたい.k 番目 (1 \leqq k \leqq N) の患者はマス (X_k, Y_k) にいる.
救急車は以下の規則に従って患者を搬送する.
- それぞれの救急車は,時刻 0 以降に動き出すことができ,病院を出発し患者の存在するマスまで移動して患者を乗せ,再び病院まで移動して患者を降ろすことを繰り返す.
- それぞれの救急車は高々 1 人の患者を乗せることができる.
- それぞれの救急車は,その救急車が設置されている病院にしか患者を搬送することができず,病院が存在しないマスで患者を降ろしてはならない.
- それぞれの救急車は,1 単位時間かけて上下左右いずれかに隣接するマスに移動することができ,患者を乗せるのにかかる時間および降ろすのにかかる時間は無視できる.
- 異なる病院に設置されている救急車が同時に同じマスに存在することは可能である.
残念ながら,ビ太郎は自分の想定したシナリオの結果を調べることはできなかったため,あなたに代わりに調べるよう依頼してきた.
IOI 王国の領土の大きさおよびビ太郎が想定したシナリオの情報が与えられたとき,時刻 T までにすべての患者をいずれかの病院に搬送することができるかどうかを求めるプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
L N T X_1 Y_1 X_2 Y_2 \vdots X_N Y_N
出力
標準出力に,ビ太郎が想定したシナリオにおいて時刻 T までにすべての患者をいずれかの病院に搬送することができるなら Yes を,そうでないなら No を 1 行に出力せよ.
制約
- 3 \leqq L \leqq 10\, 000.
- 1 \leqq N \leqq 160.
- 1 \leqq T \leqq 20\, 000.
- 1 \leqq X_k \leqq L (1 \leqq k \leqq N)
- 1 \leqq Y_k \leqq L (1 \leqq k \leqq N)
- (X_k, Y_k) は (1, 1), (1, L), (L, 1), (L, L) のいずれでもない (1 \leqq k \leqq N).
- 入力される値はすべて整数である.
小課題
- (5 点) T \leqq 50.
- (10 点) T \leqq 160.
- (8 点) N \leqq 10.
- (21 点) N \leqq 20.
- (17 点) N \leqq 45.L は奇数であり,Y_k = \frac{L+1}{2} (1 \leqq k \leqq N).
- (29 点) N \leqq 45.
- (10 点) 追加の制約はない.
入力例 1
6 4 8 1 3 2 2 3 4 5 5
出力例 1
Yes
1 番目と 2 番目の患者をマス (1, 1) にある病院へ,3 番目の患者をマス (1, 6) にある病院へ,4 番目の患者をマス (6, 6) にある病院へそれぞれ搬送することで,時刻 8 までにすべての患者をいずれかの病院に搬送することができるので,Yes を出力する.
例えば,マス (1, 1) にある病院に設置された救急車が次の順に動くと,この救急車は時刻 8 までに 1 番目と 2 番目の患者を病院へ搬送することができる.
| 時刻 | 救急車の状態 |
|---|---|
| 0 | マス (1, 1) を出発する |
| 1 | マス (2, 1) に到着する |
| 2 | マス (2, 2) に到着し,2 番目の患者を乗せ,出発する |
| 3 | マス (1, 2) に到着する |
| 4 | マス (1, 1) に到着し,2 番目の患者を降ろし,出発する |
| 5 | マス (1, 2) に到着する |
| 6 | マス (1, 3) に到着し,1 番目の患者を乗せ,出発する |
| 7 | マス (1, 2) に到着する |
| 8 | マス (1, 1) に到着し,1 番目の患者を降ろす |
この入力例は小課題 1,2,3,4,6,7 の制約を満たす.
入力例 2
9 5 19 5 5 5 5 7 5 2 5 9 5
出力例 2
No
時刻 19 までにすべての患者をいずれかの病院に搬送することはできないので,No を出力する.
この入力例はすべての小課題の制約を満たす.
入力例 3
7 7 16 6 1 2 4 4 5 5 5 3 4 6 4 5 1
出力例 3
Yes
この入力例は小課題 1,2,3,4,6,7 の制約を満たす.
入力例 4
200 15 800 126 45 196 40 43 58 96 13 28 33 44 55 60 22 58 156 135 183 44 29 92 182 157 138 30 132 175 87 166 57
出力例 4
No
この入力例は小課題 4,6,7 の制約を満たす.
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点: 100 点
注意
- 300 回のクエリを行うと,ジャッジ側・入出力の合計で最大 1200 ms を消費します.
- テストケース数が多いため,正解できない入力では早期終了することを推奨します.
あなたは JOI 銀河で怪盗として活躍している.
JOI 銀河には 0 から N - 1 までの番号が付けられている N 個の星がある.また,0 から M - 1 までの番号が付けられている M 個のワープ装置がある.ワープ装置 i (0 \leqq i \leqq M - 1) は星 U_i と星 V_i の間を双方向に結んでいる.どの 2 つの星の間も,いくつかのワープ装置を用いることで移動できる.
JOI 銀河のある星には鍵が隠されており,別の星には宝箱が隠されている.あなたのミッションは,鍵と宝箱が隠されている星の番号を特定することである.そのために,以下の質問を 300 回まで行うことができる.
- それぞれのワープ装置 i (0 \leqq i \leqq M - 1) について,星 U_i から星 V_i へ一方向のみに結ぶようにするか星 V_i から星 U_i へ一方向のみに結ぶようにするかを選択する.
- そのもとで,いくつかのワープ装置を用いて鍵のある星から宝箱のある星へ移動できるかを尋ねる.
あなたは質問を行うことで,鍵が隠された星の番号である A と宝箱が隠された星の番号である B を特定したい.ミッションで高い評価を得るために,質問の回数はできるだけ少なくしたい.
銀河の情報が与えられたとき,質問を行うことで,鍵が隠された星の番号 A と宝箱が隠された星の番号 B を特定するあなたの戦略を実装したプログラムを作成せよ.
入出力
この問題は インタラクティブ問題(あなたが作成したプログラムとジャッジプログラムが標準入出力を介して対話を行う形式の問題)である.
最初に,銀河の情報が以下の形式で標準入力から与えられる.
N M
U_0 V_0
U_1 V_1
\vdots
U_{M-1} V_{M-1}
あなたのプログラムはこれを受け取った後,採点プログラムとやり取りを行わなければならない.
質問を行うには,以下の形式で採点プログラムとやり取りせよ.
- まず,以下の形式で標準出力に出力せよ.
? x_0 x_1 x_2 \cdots x_{M - 1}- 0 \leqq i \leqq M - 1 について,x_i は文字
0または1であり,これらの間には空白を入れず長さ M の文字列として出力せよ(?の直後にのみ空白を入れること). この文字列の長さが M でない場合,不正解 [1] と判定される. - 0 \leqq i \leqq M - 1 について,x_i が
0でも1でもない場合,不正解 [2] と判定される. - 0 \leqq i \leqq M - 1 について,x_i が
0のときワープ装置 i について,星 U_i から星 V_i へ一方向に結ぶようにすることを,1のときワープ装置 i について,星 V_i から星 U_i へ一方向に結ぶようにすることを表す.
- 0 \leqq i \leqq M - 1 について,x_i は文字
- その後,質問の回答を表す整数 r が以下の形式で標準入力から与えられる.
r
ここで,r は 0, 1, -1 のいずれかであり,それぞれ以下を表す.- r が 0 のとき,星 A から星 B へ移動できないことを表す.
- r が 1 のとき,星 A から星 B へ移動できることを表す.
- r が -1 のとき,採点プログラムがあなたのプログラムを不正解であると判定したことを表す.この場合,ただちにあなたのプログラムを終了せよ.
質問を 300 回を超えて行ってはならない.300 回を超えて行った場合,不正解 [3] と判定される.
鍵が隠された星の番号と宝箱が隠された星の番号を解答するには,以下の形式で標準出力に出力せよ.
! A B
- A は 0 以上 N - 1 以下の整数である.鍵が隠された星の番号 A を表す.
- A は,0 以上 N - 1 以下でなければならない.これが満たされていない場合,不正解 [4] と判定される.
- B は 0 以上 N - 1 以下の整数である.宝箱が隠された星の番号 B を表す.
- B は,0 以上 N - 1 以下でなければならない.これが満たされていない場合,不正解 [5] と判定される.
- 誤った星の番号を解答した場合,不正解 [6] と判定される.
- 解答はちょうど 1 回行わなければならない.2 回以上解答した場合,不正解 [7] と判定される.あなたのプログラムの実行の終了時に解答が 1 回も行われていなかった場合,不正解 [8] と判定される.
上にあげたいずれでもない形式で標準出力に出力した場合,不正解 [9] と判定される.
重要な注意
- 各出力の最後には,必ず標準出力を flush せよ.flush しない場合,実行時間制限超過と判定される可能性がある.
- C++ のプログラムを提出する場合,
cout << endl;によって,改行されるとともに自動的に flush される.もしprintfを使用する場合,fflush(stdout)を用いよ. - Python のプログラムを提出する場合,入力に
input()を使う限り自動的に flush される. - 質問の際に -1 を受け取った場合,ただちにプログラムを終了せよ.終了しなかった場合,実行結果は不定である.
採点に関する注意
いくつかのテストケースについて,実際の採点プログラムは適応的 (adaptive) である.これは,採点プログラムは初めから固定された答えを持たず,それ以前の質問に応じて採点プログラムが応答するということである.ただし,すべての応答に矛盾しないような答えが少なくとも 1 つ存在するということが保証される.
テストツール
作成したプログラムをテストするためのテストツール testing_tool.py が,コンテストサイトからダウンロードできるアーカイブの中に含まれている.このツールを必ずしも使う必要はなく,また変更することも許される.実際の採点プログラムはテストツールとは異なることに注意すること.特に,テストツールは適応的 (adaptive) でなく,初めから固定された答えを持つ.
あなたのプログラムが C++ で実装されている場合,作成したプログラムをテストするには,以下のような手順に従えばよい.
- あなたのプログラムをコンパイルして実行ファイルを生成せよ.例えば,あなたのプログラムが
thief.cppという名前の場合,以下のようなコマンドを実行すればthiefという実行ファイルが生成される.g++ -std=gnu++20 -O2 -o thief thief.cpp - 次に,以下のコマンドを実行せよ.
python3 testing_tool.py ./thief
あなたのプログラムが Python で実装されている場合,例えば,あなたのプログラムが thief.py という名前なら,以下のコマンドを実行せよ.
python3 testing_tool.py pypy3 thief.py
テストツールの入力
テストツールは標準入力から以下の形式で入力を読み込む.
N M A B
U_0 V_0
U_1 V_1
\vdots
U_{M-1} V_{M-1}
テストツールの出力
プログラムの実行が正常に終了した場合,テストツールは標準出力へ以下の情報を出力する(引用符は実際には出力されない).
- 正解の場合,質問の回数が
Accepted: 25のように出力される. - 不正解の場合,不正解の種類が
Wrong Answer [4]のように出力される.
実行するプログラムが複数の不正解の条件を満たした場合,表示される不正解の種類はそれらのうち 1 つのみである.
制約
すべての入力データは以下の条件を満たす.
- 2 \leqq N \leqq 10\,000.
- 1 \leqq M \leqq 15\,000.
- 0 \leqq A \leqq N - 1.
- 0 \leqq B \leqq N - 1.
- A \neq B.
- 0 \leqq U_i < V_i \leqq N - 1 (0 \leqq i \leqq M - 1).
- (U_i, V_i) \neq (U_j, V_j) (0 \leqq i < j \leqq M - 1).
- どの 2 つの星の間も,いくつかのワープ装置を用いることで移動できる.
- 入力される値はすべて整数である.
小課題
- (11 点) M = N - 1,U_i = i,V_i = i + 1 (0 \leqq i \leqq M - 1).
- (21 点) M = N - 1,U_i = 0,V_i = i + 1 (0 \leqq i \leqq M - 1).
- (4 点) M = N - 1,N \leqq 8.
- (12 点) M = N - 1,N \leqq 50.
- (8 点) M = N - 1,N \leqq 150.
- (8 点) M = N - 1,N \leqq 250.
- (32 点) M = N - 1.この小課題では,以下に従い得点が決定される.
- 小課題 7 に対応するテストケースについて,1 つでも不正解があった場合,この小課題の得点は 0 点となる.
- そうでない場合,この小課題のすべてのテストケースにおける,関数
queryの呼び出し回数の最大値を T とする.このとき,小課題の得点は以下のように決定される.- 120 < T のとき,16 点.
- 70 < T \leqq 120 のとき,24 点.
- T \leqq 70 のとき,32 点.
- (4 点) 追加の制約はない.この小課題では,以下に従い得点が決定される.
- 小課題 8 に対応するテストケースについて,1 つでも不正解があった場合,この小課題の得点は 0 点となる.
- そうでない場合,この小課題のすべてのテストケースにおける,関数
queryの呼び出し回数の最大値を T とする.このとき,小課題の得点は以下のように決定される.- 120 < T のとき,2 点.
- 70 < T \leqq 120 のとき,3 点.
- T \leqq 70 のとき,4 点.
小課題 1,2,3,4,5,6 の得点は質問の回数によらない (300 回以下であればよい) が,70 回より多い場合はコンテストサイトにおいて「出力は部分的に正しい」と表記されることがある.
やりとりの例
テストツールが読み込む入力の例と,それに対応するやり取りの例を以下に示す.
入力例 1
5 4 0 4 0 1 0 3 1 2 1 4

1 回目の質問に対応する選択は以下のようになる.
- ワープ装置 0 について,星 0 から星 1 へ一方向に結ぶようにする.
- ワープ装置 1 について,星 3 から星 0 へ一方向に結ぶようにする.
- ワープ装置 2 について,星 1 から星 2 へ一方向に結ぶようにする.
- ワープ装置 3 について,星 1 から星 4 へ一方向に結ぶようにする.
この選択のもとで,星 0 から星 4 へはワープ装置 0, 3 をこの順に用いることで移動できるため,戻り値は 1 となる.
2 回目の質問に対応する選択は以下のようになる.
- ワープ装置 0 について,星 1 から星 0 へ一方向に結ぶようにする.
- ワープ装置 1 について,星 3 から星 0 へ一方向に結ぶようにする.
- ワープ装置 2 について,星 2 から星 1 へ一方向に結ぶようにする.
- ワープ装置 3 について,星 1 から星 4 へ一方向に結ぶようにする.
この選択のもとで,星 0 から星 4 へはいくつかのワープ装置を用いて移動できないため,戻り値は 0 となる.
3 回目の質問に対応する選択は以下のようになる.
- ワープ装置 0 について,星 0 から星 1 へ一方向に結ぶようにする.
- ワープ装置 1 について,星 0 から星 3 へ一方向に結ぶようにする.
- ワープ装置 2 について,星 2 から星 1 へ一方向に結ぶようにする.
- ワープ装置 3 について,星 1 から星 4 へ一方向に結ぶようにする.
この選択のもとで,星 0 から星 4 へはいくつかのワープ装置を用いて移動できるため,戻り値は 1 となる.
4 回目の質問に対応する選択のもとで,星 0 から星 4 へはいくつかのワープ装置を用いて移動できないため,戻り値は 0 となる.
最後に,星 A が星 0 であり,星 B が星 4 であると解答している.
この入力例は小課題 3,4,5,6,7,8 の制約を満たす.コンテストサイトからダウンロードできるアーカイブの中に含まれているファイルのうち,sample-01-in.txt は入力例 1 に対応する.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
ビ太郎が通っている魔法学校では,間もなく運動会が開催される.
運動会では,スタートの魔法陣からゴールの魔法陣へ素早く移動する競技が行われる.
この競技では,N 個の魔法陣が等間隔に円形に並べられており,時計回りに 1 から N までの番号が付けられている.
それぞれの魔法陣は青色か赤色である.
この色の情報は b, r からなる長さ N の文字列 S によって与えられ,S の j 文字目 (1 \leqq j \leqq N) が b ならば魔法陣 j は青色であり,r ならば魔法陣 j は赤色である.
ビ太郎は,この競技において以下の 2 種類の移動手段を用いることができる.
- 今いる魔法陣と隣り合う魔法陣をひとつ選び,その魔法陣へ 1 秒かけて移動する. すなわち,魔法陣 j と魔法陣 j + 1 (1 \leqq j \leqq N - 1) の間か,魔法陣 1 と魔法陣 N の間を 1 秒かけて移動する.
- 今いる魔法陣と同じ色の魔法陣をひとつ選び,その魔法陣へ 1 秒かけて移動する.
いま,魔法陣の数や色の情報は分かっているが,どの魔法陣がスタートとゴールであるかは運動会当日にならないと分からない. そこで,スタートとゴールの魔法陣の組を Q パターン考え,それぞれについて何秒かかるかを予め求めておくことにした. パターン i (1 \leqq i \leqq Q) において,スタートは魔法陣 X_i,ゴールは魔法陣 Y_i である.
魔法陣の情報とパターンの情報が与えられたとき,それぞれのパターンについてビ太郎がスタートからゴールへ移動するのに必要な時間の最小値を求めるプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
N Q S X_1 Y_1 \vdots X_Q Y_Q
出力
標準出力に Q 行出力せよ. i 行目 (1 \leqq i \leqq Q) には,ビ太郎が魔法陣 X_i から Y_i へ移動するのに必要な時間の最小値 (秒) を出力せよ.
制約
- 3 \leqq N \leqq 500\,000.
- 1 \leqq Q \leqq 500\,000.
- S は
b,rからなる長さ N の文字列である. - 1 \leqq X_i \leqq N (1 \leqq i \leqq Q).
- 1 \leqq Y_i \leqq N (1 \leqq i \leqq Q).
- X_i \neq Y_i (1 \leqq i \leqq Q).
- N, Q, X_i, Y_i は整数である (1 \leqq i \leqq Q).
小課題
- (6 点) N = 3,Q \leqq 100.
- (13 点) S は 1 文字目のみ
bであり,2 文字目以降はすべてrである. - (18 点) N は偶数であり,S は奇数文字目が
b,偶数文字目がrである. - (23 点) N は偶数であり,S は前半の \frac{N}2 文字が
b,後半の \frac{N}2 文字がrである. - (21 点) N \leqq 100,Q \leqq 100.
- (19 点) 追加の制約はない.
入力例 1
5 2 rbrbb 5 3 4 5
出力例 1
2 1
この例においては,赤色,青色,赤色,青色,青色の魔法陣がこの順に円形に並べられている.
パターン 1 について,ビ太郎は以下のようにして魔法陣 5 から魔法陣 3 へ 2 秒で移動することができる:
- 魔法陣 5 と魔法陣 1 は隣り合っているため,魔法陣 5 から魔法陣 1 へ 1 秒で移動する.
- 魔法陣 1 と魔法陣 3 は共に赤色であるため,魔法陣 1 から魔法陣 3 へ 1 秒で移動する.
2 秒未満で移動することはできないため,1 行目には 2 を出力する.
パターン 2 について,ビ太郎は以下のようにして魔法陣 4 から魔法陣 5 へ 1 秒で移動することができる:
- 魔法陣 4 と魔法陣 5 は共に青色であるため,魔法陣 4 から魔法陣 5 へ 1 秒で移動する.
1 秒未満で移動することはできないため,2 行目には 1 を出力する.
この入力例は小課題 5, 6 の制約を満たす.
入力例 2
4 3 brrr 2 4 1 3 3 1
出力例 2
1 2 2
この入力例は小課題 2, 5, 6 の制約を満たす.
入力例 3
6 3 brbrbr 1 2 2 5 2 4
出力例 3
1 2 1
この入力例は小課題 3,5,6 の制約を満たす.
入力例 4
6 5 bbbrrr 2 3 2 4 2 5 2 6 2 1
出力例 4
1 2 3 2 1
この入力例は小課題 4,5,6 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
日本列島は地殻変動の盛んな列島である. 日本列島のある海域は南北 H 行,東西 W 列のマス目で表される. 北から r 行目,西から c 列目 (1 \leqq r \leqq H,1 \leqq c \leqq W) のマスをマス (r,c) と書く. 各マスは 陸 または 海 のいずれかである. 最初に海域に存在する陸はちょうど N マスであり,それ以外のマスは海である. 最初の時点でそれらの陸の位置はマス (R_1, C_1), (R_2, C_2), \dots, (R_N, C_N) である.
日本列島では毎日正午に地殻変動が起こる. t 日目 (t \geqq 1) の正午に起こる地殻変動は以下のように表される.
- 1 \leqq r \leqq H-1,1 \leqq c \leqq W のうち t 日目の朝にマス (r, c) が陸でマス (r+1, c) が海であるようなすべての (r, c) について,マス (r+1, c) が新たに陸となる.
どの陸からどの陸へも東西南北に隣り合っている陸のみを辿って到達できる場合,日本列島は連結であると定める. 地殻変動が進むにつれ日本列島が連結になることがある.
最初の時点での海域の情報が与えられたとき,地殻変動が繰り返されることで日本列島が連結になることがあるか判定し,連結になる場合には何回の地殻変動後に初めて連結になるかを求めるプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
H W N R_1 C_1 R_2 C_2 \vdots R_N C_N
出力
標準出力に,日本列島が連結になる場合には何回の地殻変動後に初めて連結になるかを 1 行で出力せよ.
ただし,最初の時点で連結である場合は 0 を出力せよ.
また,この先日本列島が連結になることがない場合は -1 を出力せよ.
制約
- 1 \leqq H \leqq 200\,000.
- 1 \leqq W \leqq 200\,000.
- 2 \leqq N \leqq \min(H \times W,\ 200\,000).
- 1 \leqq R_i \leqq H (1 \leqq i \leqq N).
- 1 \leqq C_i \leqq W (1 \leqq i \leqq N).
- (R_i, C_i) \neq (R_j, C_j) (1 \leqq i < j \leqq N).
- 入力される値はすべて整数である.
小課題
- (5 点) W = 1.
- (9 点) N = 2.
- (8 点) H \leqq 500,W \leqq 500,N \leqq 500.
- (28 点) N \leqq 2\,000.
- (13 点) H \times W \leqq 200\,000.
- (13 点) H \times N \leqq 200\,000.
- (24 点) 追加の制約はない.
入力例 1
4 4 5 1 1 1 3 3 2 3 3 4 4
出力例 1
2
以下の図は最初の時点での海域の状況である.塗りつぶされたマスが陸を表し,空白のマスが海を表す.

1 回目の地殻変動で新たに陸となるのはマス (2, 1), (2, 3), (4, 2), (4, 3) の 4 個である. 1 回目の地殻変動の直後ではマス (1, 1) からマス (4, 4) などに東西南北に隣り合っている陸のみを辿って到達できないため,日本列島は連結ではない. 以下の図は 1 回目の地殻変動の直後の海域の状況である.新たに斜線部のマスが陸となり,それ以外のマスは変化しない.
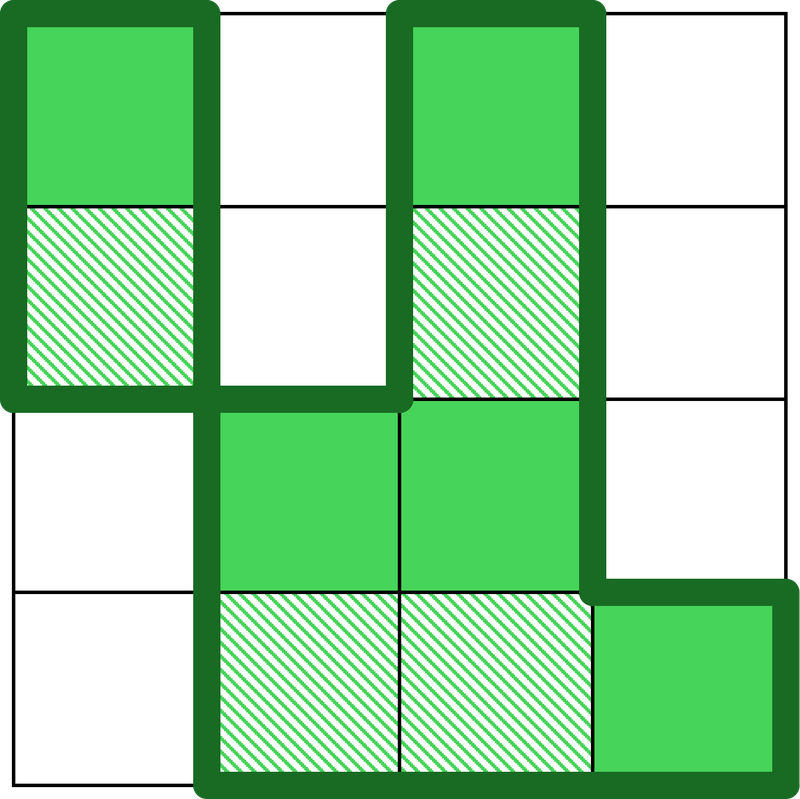
2 回目の地殻変動で新たに陸となるのはマス (3, 1) の 1 個である. 2 回目の直後の海域の状況は以下の図のようになる.
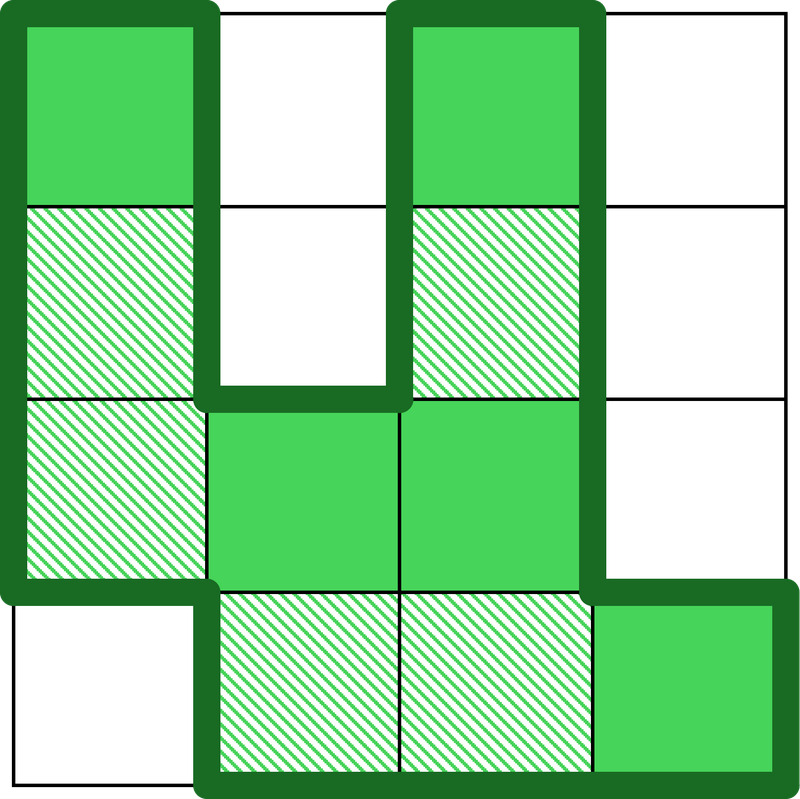
2 回目の地殻変動で初めて日本列島が連結になるため,2 を出力する.
この入力例は小課題 3, 4, 5, 6, 7 の制約を満たす.
入力例 2
3 3 2 1 1 3 3
出力例 2
-1
日本列島が連結になることはないため,-1 を出力する.
この入力例は小課題 2, 3, 4, 5, 6, 7 の制約を満たす.
入力例 3
2 2 2 1 1 1 2
出力例 3
0
地殻変動が起こる前から日本列島は連結であるため,0 を出力する.
この入力例は小課題 2, 3, 4, 5, 6, 7 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
AtCoder での提出方法について
N=4,32,48 の 3 つの入力があるので,入力で場合分けしてあなたの結果を出力してください.
K 理事長は春季トレーニングの参加者にゲームを用意した.
春季トレーニングには N 人の参加者がおり,それぞれ 1 から N までの番号が付けられている. それぞれの参加者は 1 つボードを持っている. ゲームは以下の手順で行われる.
- K 理事長は,N 人の参加者の中から 親 となる参加者を 1 人選ぶ.親でない参加者は 子 となる.どの参加者が親であるかは,参加者には伝えられない.
- K 理事長は,親のボードに文字
Tを,すべての子のボードに文字Fを書く. - 各参加者は自分のボードに書かれた文字を読む.
その後,参加者の間で事前に定めた 戦略 に従って,以下のターンを L 回行う.
- 各参加者は自分のボードに書かれた文字を消し,新たに
TかFを書き込む.その後,各参加者はボードを K 理事長に渡す. - i = 1, 2, \dots, N について,以下を行う.
- 参加者 i は,ある参加者 p (1 \leqq \mathit{p} \leqq N) を指定し,その番号 \mathit{p} を K 理事長に伝える.K 理事長は,参加者 \mathit{p} のボードを参加者 i に見せ,そのボードに書かれた文字を参加者 i は読む.このとき,参加者 i は自分自身を指定してもよい.
- 各参加者は自分のボードに書かれた文字を消し,新たに
- 各参加者は,誰が親であるかを答える.
戦略を事前にうまく定めておくことによって,親としてどの参加者が選ばれたとしても,最終的に全員が親である参加者の番号を答えられるようにすることがこのゲームの目標である. また,できるだけ小さいターン数 L で目標を達成したい.
戦略 とは,ターン数を表す非負整数 L および参加者の行動を決定する以下のような方法の組である.
- 参加者 i (1 \leqq i \leqq N) が,t ターン目 (1 \leqq t \leqq L) が始まるまでに読んだ文字が順に a_0,a_1,\ldots,a_{t - 1} であったとき,それらの情報 (i,t,a_0,a_1,\ldots,a_{t - 1}) のみから,参加者 i が t ターン目でボードに書く文字および指定する参加者の番号を定める方法.
- 参加者 i (1 \leqq i \leqq N) が,L ターン目の終了までに読んだ文字が順に a_0,a_1,\ldots,a_{L} であったとき,それらの情報 (i,L,a_0,a_1,\ldots,a_{L}) のみから,参加者 i が最終的に答える参加者の番号を定める方法.
目標を達成できるようなある戦略を定め,その戦略に従ったときに,親が 1,2,\ldots,N だった場合のそれぞれについて,各参加者が各ターンにおいてボードに書く値および次に指定する参加者を出力せよ.
入力
入力は以下の形式で標準入力から与えられる.
N
出力
標準出力に,以下の形式で出力せよ.
L
\text{acts}_1
\text{acts}_2
\vdots
\text{acts}_N
\text{acts}_s は,参加者 s が親であった場合の各参加者の各ターンにおける行動を表す. \text{acts}_s は以下の形式で出力せよ.
まず 1 行目に s を出力せよ.
i + 1 行目には,参加者 i が t ターン目でボードに書く文字 c_{i,t} と指定する参加者の番号 p_{i,t} を,各ターン t (1 \leqq t \leqq L) について順に出力せよ.
s
c_{1,1} p_{1,1} c_{1,2} p_{1,2} \cdots c_{1,L} p_{1,L}
c_{2,1} p_{2,1} c_{2,2} p_{2,2} \cdots c_{2,L} p_{2,L}
\vdots
c_{N,1} p_{N,1} c_{N,2} p_{N,2} \cdots c_{N,L} p_{N,L}
出力が正しいと判定されるのは,目標を達成できるようなある戦略が存在して,出力がその戦略に従った結果であるとき,かつそのときのみである.
具体的には,出力が正しいと判定されるのは以下の 2 つの条件を共に満たした場合である.
- 任意の参加者 i (1 \leqq i \leqq N),ターン t (1 \leqq t \leqq L),参加者 x,y (1 \leqq x,y \leqq N,x \neq y) に対して,参加者 x が親であるときに参加者 i が t ターン目が始まるまでに読んだ文字の情報と,参加者 y が親であるときに参加者 i が t ターン目が始まるまでに読んだ文字の情報が等しいならば,参加者 i がターン t にボードに書き込む文字および指定する参加者が等しい.
- 任意の参加者 i (1 \leqq i \leqq N),参加者 x, y (1 \leqq x,y \leqq N,x \neq y) に対して,参加者 x が親であるときに参加者 i が L ターン目の終了までに読んだ文字の情報と,参加者 y が親であるときに参加者 i が L ターン目の終了までに読んだ文字の情報が異なる.
制約
- N は 4,32,48 のいずれかである.
採点基準
3 個の入力データの得点の合計が課題の得点である.
各入力データに対し,得点は以下のように計算される.
あなたの出力が誤っている場合,すなわちフォーマットが間違っている場合や,「目標を達成できるようなある戦略が存在して,出力がその戦略に従った結果である」という条件が満たされないとき,あなたの得点は 0 点となる.
あなたの出力が正しい場合,以下で定める点数となる.
各入力データにおける,N の値と配点は,以下の通りである.
| 小課題 | 入力データ | N | 得点 | 配点 |
|---|---|---|---|---|
| 1 | input_01.txt |
4 | 4 < L の場合 0 点 2 < L \leqq 4 の場合 16 - 7 \times (L - 2) 点 L \leqq 2 の場合 16 点 |
16 |
| 2 | input_02.txt |
32 | 27 < L の場合 0 点 8 < L \leqq 27 の場合 60 - 3 \times (L - 8) 点 L \leqq 8 の場合 60 点 |
60 |
| 3 | input_03.txt |
48 | 9 < L の場合 0 点 L \leqq 9 の場合 24 点 |
24 |
ただし,0 点の場合,採点システム上では 出力は正しくない と表示されることに注意せよ.
入力例 1
3
出力例 1
3 1 T 1 T 2 T 3 F 1 F 2 F 3 F 1 F 2 F 3 2 F 1 F 2 F 3 T 1 T 2 T 3 F 1 F 2 F 3 3 F 1 F 2 F 3 F 1 F 2 F 3 T 1 T 2 T 3
この出力例は,以下のような戦略に従った結果である.
- L = 3 とする.
- 参加者 i (1 \leqq i \leqq N) は,t (1 \leqq t \leqq L) ターン目では,自分が親であるならば
Tを,子であるならばFをボードに書く.自分が親であるかどうかは,初めに K 理事長によって自分のボードに書かれた文字を読むことで分かることに注意せよ. - 参加者 i (1 \leqq i \leqq N) は,t (1 \leqq t \leqq L) ターン目では,これまでに読んだ文字の情報に関わらず参加者 t を指定する.
- それぞれの参加者は,3 ターン目の終了時点で,自分を含むすべての参加者がボードに書いた文字を 1 回以上ずつ読んでいる.それぞれの参加者は,ボードに
Tと書いていた参加者の番号を最終的に答える.
この戦略に従った結果,親としてどの参加者が選ばれたとしても,最終的に全員が親である参加者の番号を正しく答えることができており,目標が達成されている. そのため,この出力例は正しいと判定される.
この入力例は制約を満たさず,また実際の入力データに含まれないことに注意せよ.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
勇者ビ太郎は,モンスターから村を守る防衛戦のクエストに挑もうとしている. 防衛戦の難易度は 1 以上 L 以下の整数で表され,この値は挑戦時に選択することができる. 難易度 \ell (1 \leqq \ell \leqq L) の防衛戦では,出現するモンスターの HP が (難易度 1 の場合を基準として) \ell 倍になる.
防衛戦は T 秒間行われ,N 体のモンスターが次々と現れる. モンスターには 1 から N までの番号が付けられている. 防衛戦が開始されてから t 秒後 (0 \leqq t \leqq T) のことを,時刻 t と呼ぶ. モンスター i (1 \leqq i \leqq N) は時刻 S_i (0 \leqq S_i < T) に出現し, その強さは P_i で,その HP は,防衛戦の難易度を \ell として,\ell \times H_i である.
防衛戦の間,ビ太郎は以下の操作を何度でも行うことができる.
- 現在出現しているモンスターの中から 1 体を選び,1 秒かけてそのモンスターに攻撃する.そのモンスターの HP は 1 減少する.HP が 0 になったモンスターは倒れ,これ以上攻撃することはできない.
時刻 T になると防衛戦は終了し,防衛戦の 評価値 が以下のように計算される.
- 時刻 T の直後の時点でのモンスター i (1 \leqq i \leqq N) の HP を h_i とすると,評価値は h_1 P_1 + h_2 P_2 + \dots + h_N P_N である.
評価値がクエストにより定められた基準値 m 以下であるとき,かつそのときに限り,ビ太郎はクエストを達成することができる.
より高い難易度でクエストを達成するほど報酬も豪華になるため,ビ太郎は,クエストを達成することができる最大の難易度を求めたい. しかし,基準値は事前には知らされないため,ビ太郎は,Q 個の基準値の候補 M_1, M_2, \dots, M_Q について, クエストを達成することができる最大の難易度を求めることにした.
防衛戦の情報と基準値の候補の情報が与えられたとき,それぞれの基準値の候補について,クエストを達成することが可能かどうか判定し, 可能な場合は,クエストを達成することができる最大の難易度を求めるプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
N L T S_1 H_1 P_1 S_2 H_2 P_2 \vdots S_N H_N P_N Q M_1 M_2 \vdots M_Q
出力
Q 行出力せよ.
j 行目 (1 \leqq j \leqq Q) には,m = M_j としたときの,クエストを達成することができる最大の難易度を出力せよ.どの難易度でもクエストを達成することができない場合は,代わりに 0 を出力せよ.
制約
- 1 \leqq N \leqq 6\,000.
- 1 \leqq L \leqq 10\,000\,000.
- 1 \leqq T \leqq 10^{18}.
- 0 \leqq S_i < T (1 \leqq i \leqq N).
- 1 \leqq H_i (1 \leqq i \leqq N).
- 1 \leqq P_i (1 \leqq i \leqq N).
- H_1 P_1 + H_2 P_2 + \cdots + H_N P_N \leqq 10^{11}.
- 1 \leqq Q \leqq 1\,000\,000.
- 0 \leqq M_j \leqq 10^{18} (1 \leqq j \leqq Q).
- M_1 < M_2 < \cdots < M_Q.
- 入力される値はすべて整数である.
小課題
- (5 点) N \leqq 30,Q = 1,M_1 = 0,L = 1.
- (10 点) N \leqq 30,Q = 1,M_1 = 0.
- (14 点) N \leqq 30,Q \leqq 3.
- (10 点) Q \leqq 3.
- (33 点) N \leqq 30.
- (7 点) N \leqq 400.
- (16 点) N \leqq 1\,800.
- (5 点) 追加の制約はない.
入力例 1
2 2 10 0 9 2 8 5 1 3 0 20 40
出力例 1
0 1 2
難易度 1 の防衛戦では,以下のように行動することで評価値 4 を達成することができる.評価値 3 以下を達成することはできない.
| 時刻 | 出来事 |
|---|---|
| 0 | モンスター 1 (HP 9) が出現する. |
| 0 – 8 | モンスター 1 に 8 回攻撃する.モンスター 1 の HP が 9 から 1 まで減少する. |
| 8 | モンスター 2 (HP 5) が出現する. |
| 8 – 9 | モンスター 2 に 1 回攻撃する.モンスター 2 の HP が 5 から 4 まで減少する. |
| 9 – 10 | モンスター 1 に 1 回攻撃する.モンスター 1 の HP が 1 から 0 まで減少する. |
| 10 | モンスター 1 が倒れる. |
| 10 | 防衛戦が終了する.評価値は 0 \times P_1 + 4 \times P_2 = 4 となる. |
また,難易度 2 の防衛戦では,以下のように行動することで評価値 26 を達成することができる.評価値 25 以下を達成することはできない.
| 時刻 | 出来事 |
|---|---|
| 0 | モンスター 1 (HP 18) が出現する. |
| 0 – 8 | モンスター 1 に 8 回攻撃する.モンスター 1 の HP が 18 から 10 まで減少する. |
| 8 | モンスター 2 (HP 10) が出現する. |
| 8 – 10 | モンスター 1 に 2 回攻撃する.モンスター 1 の HP が 10 から 8 まで減少する. |
| 10 | 防衛戦が終了する.評価値は 8 \times P_1 + 10 \times P_2 = 26 となる. |
さらに,この入力例においては L = 2 であるため,難易度 3 以上の防衛戦を選択することができない.したがって,出力は以下のようになる.
- 1 個目の基準値 M_1 = 0 ではどの難易度でもクエストを達成することができないため,1 行目には
0を出力する. - 2 個目の基準値 M_2 = 20 では最大で難易度 1 の防衛戦までクエストを達成することができるため,2 行目には 1 を出力する.
- 3 個目の基準値 M_3 = 40 では最大で難易度 2 の防衛戦までクエストを達成することができるため,3 行目には 2 を出力する.
この入力例は小課題 3, 4, 5, 6, 7, 8 の制約を満たす.
入力例 2
3 1 100000000000 60000000000 30000000000 1 30000000000 45000000000 1 10000000000 10000000000 1 1 0
出力例 2
0
この入力例はすべての小課題の制約を満たす.
入力例 3
3 10000000 100000000 60000000 4 1 30000000 6 1 0 2 1 1 0
出力例 3
7000000
この入力例は小課題 2, 3, 4, 5, 6, 7, 8 の制約を満たす.
入力例 4
5 20 100 0 3 1 20 2 2 40 1 3 60 4 4 80 2 5 11 0 50 100 150 200 250 300 350 400 450 500
出力例 4
6 8 10 12 13 15 16 18 19 20 20
この入力例は小課題 5, 6, 7, 8 の制約を満たす.
入力例 5
15 10000000 1000000000000 160278118759 43084 33592 442653603914 19490 23090 824219815410 50858 89563 502303340628 56629 45080 495062829942 87342 28821 234536700105 45384 34328 396080693809 78081 50812 734374391045 40873 92012 122606844331 25451 30426 204076581972 58431 13989 495156368673 54276 41670 812963939390 27614 50228 405067019838 96324 18477 464546304875 67562 45956 528559327980 41759 15546 10 216000000000000 1728000000000000 5832000000000000 13824000000000000 27000000000000000 46656000000000000 74088000000000000 110592000000000000 157464000000000000 216000000000000000
出力例 5
995176 1135557 1431775 1824183 2359362 3059523 3942014 5106209 6594716 8448125
この入力例は小課題 5, 6, 7, 8 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
葵はティーパーティーを開催しようと計画している. このティーパーティーには葵を含めた M 人が参加予定であり,参加者には 1 から M までの番号が付けられている. 葵は各参加者に,1 切れのケーキと 1 杯の紅茶を配るつもりである.
ティーパーティーのために,葵は N 切れのケーキ (N \geqq M) と M 杯の紅茶を準備した. ケーキには 1 から N まで,紅茶には 1 から M までの番号が付けられている. ケーキ i (1 \leqq i \leqq N) のブランドは A_i で,おいしさは B_i である. 紅茶 j (1 \leqq j \leqq M) のブランドは C_j で,おいしさは D_j である. 葵は参加者の 幸福度 の総和ができるだけ大きくなるように,参加者にケーキと紅茶を配りたい. 参加者 k (1 \leqq k \leqq M) にケーキ i (1 \leqq i \leqq N) と紅茶 j (1 \leqq j \leqq M) を配ったとき,参加者 k の幸福度は以下のように定まる.
- A_i = C_j のとき,参加者 k の幸福度は B_i + D_j である.
- A_i \neq C_j のとき,参加者 k の幸福度は B_i である.
葵が準備したケーキと紅茶を適切に配るとき,すべての参加者の幸福度の総和として考えられる最大値を求めよ. なお,今回配らなかったケーキについては,葵が別の日に食べるため考えなくてよいものとする.
入力
入力は以下の形式で標準入力から与えられる.
N M A_1 A_2 \cdots A_N B_1 B_2 \cdots B_N C_1 C_2 \cdots C_M D_1 D_2 \cdots D_M
出力
標準出力に,葵が準備したケーキと紅茶を適切に配るときの,すべての参加者の幸福度の総和として考えられる最大値を 1 行で出力せよ.
制約
- 1 \leqq M \leqq N \leqq 200\,000.
- 1 \leqq A_i \leqq N (1 \leqq i \leqq N).
- 0 \leqq B_i \leqq 10^9 (1 \leqq i \leqq N).
- 1 \leqq C_j \leqq N (1 \leqq j \leqq M).
- 0 \leqq D_j \leqq 10^9 (1 \leqq j \leqq M).
- 入力される値はすべて整数である.
小課題
- (8 点) D_j = 0 (1 \leqq j \leqq M).
- (19 点) B_i = 0 (1 \leqq i \leqq N).
- (31 点) A_i = i (1 \leqq i \leqq N),C_j = j (1 \leqq j \leqq M).
- (42 点) 追加の制約はない.
入力例 1
4 3 1 1 2 3 2 1 2 4 1 1 2 3 1 1
出力例 1
12
葵が準備したケーキと紅茶を適切に配るとき,すべての参加者の幸福度の総和の最大値は 12 である.
- 参加者 1 にケーキ 1 と紅茶 1 を配る.参加者 1 の幸福度は 2 + 3 = 5 である.
- 参加者 2 にケーキ 3 と紅茶 3 を配る.参加者 2 の幸福度は 2 + 1 = 3 である.
- 参加者 3 にケーキ 4 と紅茶 2 を配る.参加者 3 の幸福度は 4 である.
どのように配っても,すべての参加者の幸福度の総和が 12 より大きくならないため,12 を出力する.
この入力例は小課題 4 の制約を満たす.
入力例 2
5 3 1 2 3 4 5 4695 53325 57544 74342 81986 1 2 3 59037 23296 16434
出力例 2
232949
この入力例は小課題 3,4 の制約を満たす.
入力例 3
4 3 2 1 3 1 52 49 72 31 3 1 3 0 0 0
出力例 3
173
この入力例は小課題 1,4 の制約を満たす.
入力例 4
5 2 1 1 2 3 5 0 0 0 0 0 1 1 3 1
出力例 4
4
この入力例は小課題 2,4 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
EGOI 国では東西に N 本の電波塔が立ち並び,その間で情報の通信を行うことで,国民にインターネット通信を提供している. 電波塔には,西から順に 1 から N までの番号が付けられている. 電波塔 i (1 \leqq i \leqq N) は,西から波長が A_i 以上 A_i + L 以下の電波を受信することと,東へ波長 B_i の電波を送信することが可能である. つまり,1 \leqq i_1 < i_2 \leqq N について,A_{i_2} \leqq B_{i_1} \leqq A_{i_2} + L が成り立つとき,電波塔 i_1 から電波塔 i_2 に情報を伝達することができる.
最近の EGOI 国では,さらに安定したインターネット通信が求められている.EGOI 国政府は,「番号順に情報を伝達できるように電波塔を 1 本以上選ぶ方法の個数」を通信の安定性の基準とすることにした. 具体的には,以下の条件を満たす 1 本以上の塔の選び方の数を求めたい.
- 選んだ塔の番号を小さい方から順に i_1, i_2, \dots, i_k としたとき,すべての j (1\leqq j\leqq k-1) に対して A_{i_{j+1}} \leqq B_{i_j} \leqq A_{i_{j+1}} + L が成り立つ.
電波塔の送受信できる波長の情報が与えられたとき,条件を満たす塔の選び方の個数を 1\,000\,000\,007 で割ったあまりを求めるプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
N L A_1 B_1 A_2 B_2 \vdots A_N B_N
出力
標準出力に,条件を満たす塔の選び方の個数を 1\,000\,000\,007 で割ったあまりを 1 行で出力せよ.
制約
- 2 \leqq N \leqq 300\,000.
- 0 \leqq L \leqq 300\,000.
- 1 \leqq A_i \leqq 300\,000 (1\leqq i \leqq N).
- 1 \leqq B_i \leqq 300\,000 (1\leqq i \leqq N).
- 入力される値はすべて整数である.
小課題
- (20 点) N \leqq 16.
- (20 点) N \leqq 5\,000.
- (25 点) L = 0.
- (35 点) 追加の制約はない.
入力例 1
3 0 1 3 2 3 3 2
出力例 1
5
電波塔 1, 2, 3 を選んだ場合を考える.
- A_2 \leqq B_1 \leqq A_2 + L でないため,電波塔 1 から電波塔 2 に情報を伝達することはできない.
- A_3 \leqq B_2 \leqq A_3 + L であるため,電波塔 2 から電波塔 3 に情報を伝達することはできる.
よって,この選び方は条件を満たさない.
電波塔 1, 3 を選んだ場合を考える.
- A_3 \leqq B_1 \leqq A_3 + L であるため,電波塔 1 から電波塔 3 に情報を伝達することはできる.
よって,この選び方は条件を満たす.
条件を満たす塔の選び方は,\lbrace1\rbrace, \lbrace2\rbrace, \lbrace3\rbrace, \lbrace1, 3\rbrace, \lbrace2, 3\rbrace の 5 通りである. よって,5 を 1\,000\,000\,007 で割ったあまりである 5 を出力する.
この入力例はすべての小課題の制約を満たす.
入力例 2
8 2 1 3 5 1 6 7 7 5 5 2 2 1 3 1 1 6
出力例 2
36
この入力例は小課題 1,2,4 の制約を満たす.
入力例 3
10 3 1 5 2 3 2 4 5 4 10 7 7 9 4 3 3 7 7 7 6 5
出力例 3
109
この入力例は小課題 1,2,4 の制約を満たす.
Time Limit: 5 sec / Memory Limit: 1024 MiB
配点: 100 点
葵は N 枚のカードを持っていて,カードには 1 から N までの番号が付けられている.各カードには 1 つの正の整数が書かれており,カード i (1 \leqq i \leqq N) に書かれた整数は A_i である.
葵はカードと黒板を用いて Q 回の遊びを行う.j 回目 (1 \leqq j \leqq Q) に行う遊びは以下のようなものである.
- 黒板に 0 を書き込む.
- 机にカード L_j, L_j + 1, \dots, R_j をこの順に左から右へ一列に並べる.
- 以下の行動を R_j - L_j + 1 回行う.k 回目 (1 \leqq k \leqq R_j - L_j + 1) の行動は以下のようなものである.
- 現在黒板に書き込まれている整数を x とし,机に並べたカードの列の中で左から k 番目のカードに書かれている整数を y とする.x を黒板から消し,x + y または x - y を黒板に書き込む.x - y を黒板に書き込んだ場合,ういろう(和菓子)を 1 個食べる.
- ただし,0 より小さい整数を黒板に書き込むことはできない.
あなたは,それぞれの遊びにおいて葵が食べるういろうの個数としてありうる最大の値を知りたい.
カードと遊びの情報が与えられたとき,それぞれの遊びにおいて葵が食べるういろうの個数としてありうる最大の値を求めるプログラムを作成せよ.
入力
入力は以下の形式で標準入力から与えられる.
N A_1 A_2 \cdots A_N Q L_1 R_1 L_2 R_2 \vdots L_Q R_Q
出力
標準出力に Q 行出力せよ.j 行目 (1 \leqq j \leqq Q) には,j 回目の遊びにおいて,葵が食べるういろうの個数としてありうる最大の値を出力せよ.
制約
- 1 \leqq N \leqq 200\,000.
- 1 \leqq A_i \leqq 100 (1 \leqq i \leqq N).
- 1 \leqq Q \leqq 200\,000.
- 1 \leqq L_j \leqq R_j \leqq N (1 \leqq j \leqq Q).
- 入力される値はすべて整数である.
小課題
- (7 点) N \leqq 20,Q \leqq 20.
- (11 点) N \leqq 300,Q \leqq 20.
- (15 点) N \leqq 5\,000,Q \leqq 20.
- (24 点) Q \leqq 20.
- (21 点) A_i \leqq 2 (1 \leqq i \leqq N).
- (14 点) A_i \leqq 20 (1 \leqq i \leqq N).
- (8 点) 追加の制約はない.
入力例 1
5 3 4 7 2 8 2 1 3 4 4
出力例 1
1 0
1 回目の遊びでは,以下のような場合が考えられる.
- 最初に,黒板に 0 を書き込む.
- 次に,机にカード 1, 2, 3 をこの順に左から右へ一列に並べる.
- 現在黒板に書き込まれている整数は 0 で,机に並べたカードの列の中で左から 1 番目のカードに書かれている整数は 3 である.0 を黒板から消し,3 を黒板に書き込む.
- 現在黒板に書き込まれている整数は 3 で,机に並べたカードの列の中で左から 2 番目のカードに書かれている整数は 4 である.3 を黒板から消し,7 を黒板に書き込む.
- 現在黒板に書き込まれている整数は 7 で,机に並べたカードの列の中で左から 3 番目のカードに書かれている整数は 7 である.7 を黒板から消し,0 を黒板に書き込む.ういろうを 1 個食べる.
このとき,1 回目の遊びで葵が食べるういろうの個数は 1 個である.1 回目の遊びで葵が食べるういろうの個数は 2 個以上にならないことが示せる.したがって,1 を出力する.
2 回目の遊びでは,以下のような場合が考えられる.
- 最初に,黒板に 0 を書き込む.
- 次に,机にカード 4 を並べる.
- 現在黒板に書き込まれている整数は 0 で,机に並べたカードの列の中で左から 1 番目のカードに書かれている整数は 2 である.0 を黒板から消し,2 を黒板に書き込む.
このとき,2 回目の遊びで葵が食べるういろうの個数は 0 個である.2 回目の遊びで葵が食べるういろうの個数は 1 個以上にならないことが示せる.したがって,0 を出力する.
この入力例は小課題 1,2,3,4,6,7 の制約を満たす.
入力例 2
14 1 2 2 1 2 1 1 2 1 2 2 1 1 1 5 1 2 1 14 5 11 3 12 4 7
出力例 2
0 8 4 6 2
1 回目の遊びでは,以下のような場合が考えられる.
- 最初に,黒板に 0 を書き込む.
- 次に,机にカード 1, 2 をこの順に左から右へ一列に並べる.
- 現在黒板に書き込まれている整数は 0 で,机に並べたカードの列の中で左から 1 番目のカードに書かれている整数は 1 である.0 を黒板から消し,1 を黒板に書き込む.
- 現在黒板に書き込まれている整数は 1 で,机に並べたカードの列の中で左から 2 番目のカードに書かれている整数は 2 である.1 を黒板から消し,3 を黒板に書き込む.
このとき,1 回目の遊びで葵が食べるういろうの個数は 0 個である.1 回目の遊びで葵が食べるういろうの個数は 1 個以上にならないことが示せる.したがって,0 を出力する.
この入力例はすべての小課題の制約を満たす.
入力例 3
8 16 23 45 76 43 97 12 43 7 1 8 3 7 2 7 4 5 5 8 2 6 3 5
出力例 3
3 2 2 1 2 2 1
この入力例は小課題 1,2,3,4,7 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
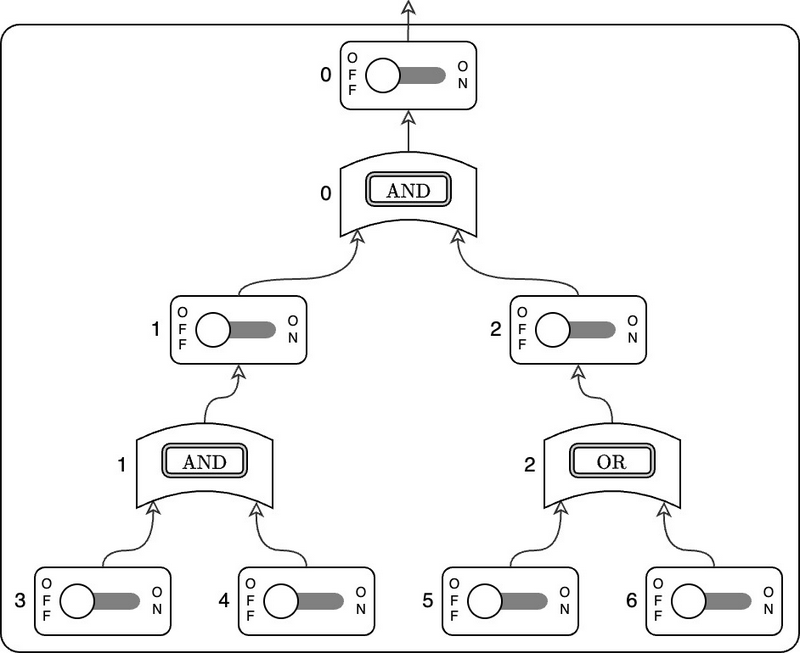
JOI 君は電子回路セットで遊んでいる. 電子回路セットは N 個の AND 部品,N 個の OR 部品 と,1 個の 回路ボード からなる. 回路ボードは 2N+1 個の スイッチ と N 個の 部品スロット で構成され, 各部品スロットに AND 部品か OR 部品を設置することで使用することができる. 回路ボードは,設置された部品とスイッチの状態に応じて,以下のように 0 または 1 の値を出力する.
回路ボードの仕様
- スイッチには 0 から 2N までの番号が付けられており,各スイッチは ON または OFF の状態を持つ.各スイッチは下に書かれたように 0 または 1 の値を出力する.
- 部品スロットには 0 から N-1 までの番号が付けられている.各部品スロットは下に書かれたように 0 または 1 の値を出力する.
- 各スイッチおよび各部品スロットの出力は,以下の規則によって番号の大きなものから順(同じ番号のスイッチと部品スロットについては部品スロットが先)に定まる.
- j = 2N, 2N-1, \dots, N について,スイッチ j は以下を出力する.
- スイッチ j が OFF であるとき,0 を出力する.
- スイッチ j が ON であるとき,1 を出力する.
- j = N-1, N-2, \dots, 0 について,部品スロット j の出力を x としたとき,スイッチ j は以下を出力する.
- スイッチ j が OFF であるとき,x を出力する.
- スイッチ j が ON であるとき,1-x を出力する
- i = N-1, N-2, \dots, 0 について,部品スロット i は 2 個のスイッチ U_i, V_i と接続している.ここで,U_i, V_i は i < U_i < V_i \leqq 2N を満たす.スイッチ U_i の出力を x,スイッチ V_i の出力を y としたとき,部品スロット i は以下を出力する.
- 部品スロット i に AND 部品が設置されているとき,\min(x, y) を出力する.
- 部品スロット i に OR 部品が設置されているとき,\max(x, y) を出力する.
- j = 2N, 2N-1, \dots, N について,スイッチ j は以下を出力する.
- j = 1, 2, \dots, 2N について,U_i = j または V_i = j であるような i (0 \leqq i \leqq N - 1) がただ 1 つ存在する.
- 回路ボードの出力は,スイッチ 0 の出力と等しい.
例えば,N = 3, U_0 = 1, V_0 = 2, U_1 = 3, V_1 = 4, U_2 = 5, V_2 = 6 で,部品スロット 0, 1, 2 にそれぞれ AND 部品,AND 部品,OR 部品が設置されている場合,回路ボードは以下の図のように表される.
さて,JOI 君がすべての部品スロットに AND 部品を設置しようとしたところ,設置した部品の中に 最大 R 個 の OR 部品がまぎれ込んでいることが明らかになった. AND 部品と OR 部品は見た目で区別することができないため,回路ボードを使用して AND 部品と OR 部品を区別しなければならない. あなたの仕事は,JOI 君に以下の形式の質問を 1\,000 回まで行い,どの部品スロットに OR 部品が設置されているかを特定することである.
- あなたは JOI 君に 2N+1 個のスイッチをどのような状態にするか指示する.JOI 君は指示された通りにスイッチの状態を変更し,回路ボードの出力をあなたに教える.
回路ボードの回路の接続の情報と設置されている OR 部品の個数の上限が与えられたとき,1\,000 回以下の質問で,どの部品スロットに OR 部品が設置されているかを特定するプログラムを作成せよ
実装の詳細
あなたは 1 つのファイルを提出しなければならない.
あなたの提出するファイルは circuit.cpp という名前である.
そのプログラムは #include プリプロセッサ指令によって circuit.h を読み込むこと.
circuit.cpp は以下の関数を実装していなければならない.
std::string solve(int N, int R, std::vector<int> U, std::vector<int> V)- この関数は各テストケースにおいて 1 回だけ呼び出される.
- 引数
Nは部品スロットの個数 N である. - 引数
Rは設置されている OR 部品の個数の上限 R である. - 引数
U,Vは長さ N の配列であり,U[i],V[i](0 \leqq i \leqq N - 1) は部品スロット i に接続されているスイッチの番号 U_{i}, V_{i} である. - この関数は,以下の条件を満たす
&と|からなる長さ N の文字列 t を返さなければならない.- 各 i = 0, 1, \dots, N-1 について,部品スロット i に設置されている部品が AND 部品ならば
t[i]は&であり,OR 部品ならばt[i]は|である.
- 各 i = 0, 1, \dots, N-1 について,部品スロット i に設置されている部品が AND 部品ならば
- 戻り値 t の長さが N でない場合,不正解[1] と判定される.
- 戻り値 t に
&でも|でもない文字が含まれる場合,不正解[2] と判定される. - 実際に各部品スロットに設置されている部品の種類が,戻り値 t の表すものと異なる場合,不正解[3] と判定される.
あなたのプログラムは以下の関数を呼び出すことができる.
int query(std::string s)- あなたはこの関数を用いて JOI 君に質問をすることができる.
- 引数
sは0と1からなる長さ 2N + 1 の文字列でなければならない.各 j = 0, 1, \dots, 2N について,s[j]が0ならばスイッチ j を OFF にすることを,s[j]が1ならばスイッチ j を ON にすることを表す. - 引数
sの長さが 2N+1 でない場合,不正解[4] と判定される. - 引数
sに0でも1でもない文字が含まれる場合,不正解[5] と判定される. - この関数を 1\,000 回より多く呼び出してはならない.1\,000 回より多く呼び出した場合,不正解[6] と判定される.
- この関数の戻り値は,引数
sの通りにスイッチの状態を変更したときの回路ボードの出力である.
重要な注意
- 内部での使用のために他の関数を実装したり,グローバル変数を宣言するのは自由である.
- あなたの提出したプログラムは,標準入力・標準出力,あるいは他のファイルといかなる方法でもやりとりしてはならない.ただし,標準エラー出力にデバッグ情報等を出力することは許される.
コンパイル・実行の方法
作成したプログラムをテストするための,採点プログラムのサンプルが, コンテストサイトからダウンロードできるアーカイブの中に含まれている. このアーカイブには,提出しなければならないファイルのサンプルも含まれている.
採点プログラムのサンプルは 1 つのファイルからなる.
そのファイルは grader.cpp である.
作成したプログラムをテストするには,
これらのファイル grader.cpp, circuit.cpp, circuit.h を同じディレクトリに置き,次のようにコマンドを実行する.
g++ -std=gnu++20 -O2 -o grader grader.cpp circuit.cpp
なお,アーカイブの中に含まれている compile.sh というファイルを代わりに実行してもよい.その場合,次のようにコマンドを実行する.
./compile.sh
コンパイルが成功すれば,grader という実行ファイルが生成される.
実際の採点プログラムは,採点プログラムのサンプルとは異なることに注意すること. 採点プログラムのサンプルは単一のプロセスとして起動する. このプログラムは,標準入力から入力を読み込み,標準出力に結果を出力する.
採点プログラムのサンプルの入力
T を関数 solve が返すべき長さ N の文字列とする.採点プログラムのサンプルは標準入力から以下の形式で入力を読み込む.
N R
U_0 V_0
U_1 V_1
\vdots
U_{N-1} V_{N-1}
T
採点プログラムのサンプルの出力
採点プログラムのサンプルは標準出力へ以下の情報を出力する.
- 正解の場合,関数
queryの呼び出し回数がAccepted: 22のように出力される. - 不正解の場合,不正解の種類が
Wrong Answer [4]のように出力される.
採点プログラムのサンプルは,いずれかの不正解の条件が満たされた時点で実行を終了する. 実行するプログラムが複数の不正解の条件を満たした場合,表示される不正解の種類はそれらのうち 1 つのみである.
採点に関する注意
実際の採点プログラムは適応的 (adaptive) ではなく,やりとりの初めから固定された答えを持つ.
制約
- 1 \leqq N \leqq 8\,000.
- 1 \leqq R \leqq \min(N, 120).
- i < U_i < V_i \leqq 2N (0 \leqq i \leqq N - 1).
- j = 1, 2, \dots, 2N について,U_i = j または V_i = j であるような i (0 \leqq i \leqq N - 1) がただ 1 つ存在する.
小課題
- (1 点) N = 1.
- (8 点) N \leqq 1\,000,R = 1.
- (10 点) N \leqq 1\,000.
- (21 点) U_i = i + 1,V_i = N + 1 + i (0 \leqq i \leqq N - 1),R \leqq 70.
- (9 点) U_i = i + 1,V_i = N + 1 + i (0 \leqq i \leqq N - 1).
- (25 点) U_i = 2i + 1,V_i = 2i + 2 (0 \leqq i \leqq N - 1),R \leqq 70.
- (9 点) U_i = 2i + 1,V_i = 2i + 2 (0 \leqq i \leqq N - 1).
- (14 点) R \leqq 70.
- (3 点) 追加の制約はない.
やりとりの例
採点プログラムのサンプルが読み込む入力の例と,それに対応する関数の呼び出しの例を以下に示す.
入力例 1
1 1 1 2 |

1 回目の query の呼び出しでは,回路ボードの出力は以下のように計算できる.
- スイッチ 1, 2 の状態はそれぞれ ON, OFF であるから,スイッチ 1, 2 はそれぞれ 1, 0 を出力する.
- 部品スロット 0 には OR 部品が設置されていて,接続するスイッチ 1, 2 はそれぞれ 1, 0 を出力しているから,部品スロット 0 は \max(1, 0) = 1 を出力する.
- スイッチ 0 の状態は OFF で,部品スロット 0 の出力は 1 であるから,スイッチ 0 の出力は 1 である.
- したがって,回路ボードの出力は 1 である.
この入力例はすべての小課題の制約を満たす.
入力例 2
3 3 1 2 3 4 5 6 &&|
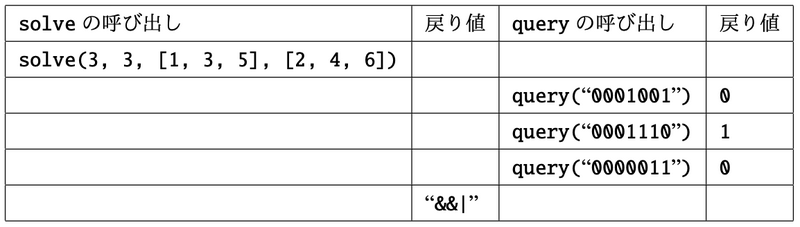
問題文中の図がこの入力例の回路ボードを表している.
この入力例は小課題 3, 6, 7, 8, 9 の制約を満たす.
コンテストサイトからダウンロードできるファイルのうち,sample-01-in.txt は入力例 1 に対応し,sample-02-in.txt は入力例 2 に対応する.
また,sample-03-in.txt は小課題 3, 4, 5, 8, 9 の制約を満たし,sample-04-in.txt は小課題 3, 6, 7, 8, 9 の制約を満たす.