JOIG 2023/2024 本選過去問

A - 三連続 (Three Consecutive)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

長さ N の文字列 S が与えられる．S の各文字は o か x のいずれかである．

S に o が 3 つ連続している箇所があれば Yes を，そうでないならば No を， 1 行で出力せよ．

ただし， o が 3 つ連続している箇所の隣に o があっても良いものとする．

制約

1 \leqq N \leqq 100\,000．
S は長さ N の文字列である．
S の各文字は o か x のいずれかである．
N は整数である．

小課題

(40 点) N=5．
(60 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N
S

出力

S に o が 3 つ連続している箇所があれば Yes を，そうでないならば No を出力せよ．

入力例 1

5
oxooo

出力例 1

Yes

S の 3,4,5 文字目は o であり，o が 3 つ連続しているため，Yes を出力する．

この入力例は小課題 1, 2 の制約を満たす．

入力例 2

5
xooxo

出力例 2

No

S に o が 3 つ連続している箇所は無いため，No を出力する．

この入力例は小課題 1, 2 の制約を満たす．

入力例 3

1
o

出力例 3

No

S に o が 3 つ連続している箇所は無いため，No を出力する．

この入力例は小課題 2 の制約を満たす．

入力例 4

10
oooooooooo

出力例 4

Yes

例えば，S の 1,2,3 文字目は o であり，o が 3 つ連続しているため，Yes を出力する．

o が 3 つ連続している箇所の隣に o があっても良いことに注意せよ．

この入力例は小課題 2 の制約を満たす．

入力例 5

20
xooxxoooxoxooxooxoox

出力例 5

Yes

この入力例は小課題 2 の制約を満たす．

入力例 6

20
xooxxxooxoxooxooxoox

出力例 6

No

この入力例は小課題 2 の制約を満たす．

B - ダンス (Dance)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 中学校のあるクラスには 2N 人の生徒がいる．各生徒の身長は A_1, A_2, \dots, A_{2N} である．

今度の体育の授業で，生徒は N 組の 2 人組に分かれてダンスを踊る．

このクラスでは，2 人組の作り方を工夫して美しいダンスを実現しようとしている．美しいダンスを実現するには，すべての 2 人組の身長の差が D 以下である必要がある．

各生徒の身長が与えられたとき，美しいダンスが実現可能かどうかを判定するプログラムを作成せよ．

制約

1 \leqq N \leqq 100．
0 \leqq D \leqq 100．
1 \leqq A_i \leqq 100 (1 \leqq i \leqq 2N)．
入力される値はすべて整数である．

小課題

(20 点) N = 1．
(40 点) D = 0．
(40 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N D
A_1 A_2 \dots A_{2N}

出力

美しいダンスが実現可能な場合 Yes を，そうでない場合 No を 1 行で出力せよ．

入力例 1

1 5
2 7

出力例 1

Yes

身長が 2 の生徒と身長が 7 の生徒が 2 人組を作ると，2 人の身長の差は 5 であり，これは D = 5 以下なので，美しいダンスが実現できる．したがって，Yes を出力する．

この入力は小課題 1, 3 の制約を満たす．

入力例 2

3 0
10 10 10 11 10 10

出力例 2

No

すべての 2 人組の身長の差が 0 以下であるような 2 人組の作り方は存在しない．したがって，No を出力する．

この入力は小課題 2, 3 の制約を満たす．

入力例 3

6 4
22 15 32 36 16 30 42 30 39 23 17 18

出力例 3

Yes

以下のように 2 人組を作ることで，すべての 2 人組の身長の差が 4 以下となり，美しいダンスが実現できる．

身長が 39 の生徒と身長が 42 の生徒が 2 人組を作る．
身長が 22 の生徒と身長が 23 の生徒が 2 人組を作る．
身長が 16 の生徒と身長が 17 の生徒が 2 人組を作る．
身長が 32 の生徒と身長が 36 の生徒が 2 人組を作る．
身長が 15 の生徒と身長が 18 の生徒が 2 人組を作る．
身長が 30 の生徒と身長が 30 の生徒が 2 人組を作る．

したがって，Yes を出力する．

この入力は小課題 3 の制約を満たす．

C - 座席 2 (Seats 2)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 国では，今年プログラミングの世界大会が開かれることとなった．大会には N 人の選手が参加予定であり，選手には 1 から N までの番号が付けられている．

各選手の出身国は 1 以上 10^9 以下の整数の番号で表され，選手 i (1 \leqq i \leqq N) の出身国は国 C_i である．N 人の選手の出身国がすべて同じであることはない．また，各選手の座席は直線状に並んでおり，選手 i (1 \leqq i \leqq N) の座席は位置 X_i にある．選手 i (1 \leqq i \leqq N) と選手 j (1 \leqq j \leqq N) の座席の距離は |X_i - X_j| である．ただし，|x| は x の絶対値を表す．

各選手は大会中他の選手と交流をするにあたって，自分とは出身国の異なる選手のうち，自分と座席が最も近い選手までの座席の距離を知りたい．

各選手の出身国と座席の位置の情報が与えられたとき，各選手 i (1 \leqq i \leqq N) について，選手 i とは出身国の異なる選手のうち，選手 i との座席の距離が最も小さい選手までの座席の距離を出力するプログラムを作成せよ．

制約

2 \leqq N \leqq 300\,000．
1 \leqq C_i \leqq 10^9 (1 \leqq i \leqq N)．
1 \leqq X_i \leqq 10^9 (1 \leqq i \leqq N)．
N 人の選手の出身国がすべて同じであることはない．
入力される値はすべて整数である．

小課題

(20 点) N \leqq 1\,000．
(40 点) C_i \leqq 10 (1 \leqq i \leqq N)．
(40 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N
C_1 X_1
C_2 X_2
\vdots
C_N X_N

出力

N 行出力せよ．i 行目 (1 \leqq i \leqq N) には，選手 i とは出身国の異なる選手のうち，選手 i との座席の距離が最も小さい選手までの座席の距離を出力せよ．

入力例 1

出力例 1

3
4
3

選手 1 の出身国は国 2 であり，選手 1 と出身国の異なる選手は選手 2, 3 である．これらの選手のうち，選手 1 との座席の距離が最も小さい選手は選手 3 であり，その座席の距離は 3 である．したがって，1 行目には 3 を出力する．
選手 2 の出身国は国 1 であり，選手 2 と出身国の異なる選手は選手 1 のみである．選手 2 と選手 1 の座席の距離は 4 なので，2 行目には 4 を出力する．
選手 3 の出身国は国 1 であり，選手 3 と出身国の異なる選手は選手 1 のみである．選手 3 と選手 1 の座席の距離は 3 なので，3 行目には 3 を出力する．

この入力例は小課題 1, 2, 3 の制約を満たす．

入力例 2

出力例 2

この入力例は小課題 1, 2, 3 の制約を満たす．

入力例 3

出力例 3

0
0
0

同じ位置に複数の選手の座席があることもある．

この入力例は小課題 1, 2, 3 の制約を満たす．

D - たくさんの数字 (Many Digits)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 高校の葵さんは，N 行 N 列のマス目の各マスに整数を十進数表記で書くことにした．具体的には上から i 行目 (1 \leqq i \leqq N)，左から j 列目 (1 \leqq j \leqq N) のマスには A_i + B_j を十進数表記で書く．

葵さんは数字を何文字書くことになるかを知りたい．つまり，葵さんが書く N^2 個の整数の桁数の合計を求めたい．

A_i (1 \leqq i \leqq N) と B_j (1 \leqq j \leqq N) が与えられたとき，葵さんが書く N^2 個の整数の桁数の合計を求めるプログラムを作成せよ．

制約

1 \leqq N \leqq 150\,000．
1 \leqq A_i \leqq 999\,999\,999 (1 \leqq i \leqq N)．
1 \leqq B_j \leqq 999\,999\,999 (1 \leqq j \leqq N)．
入力される値はすべて整数である．

小課題

(5 点) N = 1．
(11 点) N \leqq 2\,000．
(15 点) A_i \leqq 2\,000 (1 \leqq i \leqq N)，B_j \leqq 2\,000 (1 \leqq j \leqq N)．
(8 点) 100\,000\,000 \leqq A_i \leqq 500\,000\,000 (1 \leqq i \leqq N)，100\,000\,000 \leqq B_j \leqq 500\,000\,000 (1 \leqq j \leqq N)．
(22 点) 100\,000\,000 \leqq A_i (1 \leqq i \leqq N)，100\,000\,000 \leqq B_j (1 \leqq j \leqq N)．
(12 点) A_i \leqq 150\,000 (1 \leqq i \leqq N)，B_j = j (1 \leqq j \leqq N)．
(13 点) B_j = j (1 \leqq j \leqq N)．
(14 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N
A_1 A_2 \cdots A_N
B_1 B_2 \cdots B_N

出力

葵さんが書く N^2 個の整数の桁数の合計を 1 行で出力せよ．

入力例 1

3
97 79 7
20 2 21

出力例 1

葵さんが各マスに書く整数は以下の図のようになる．

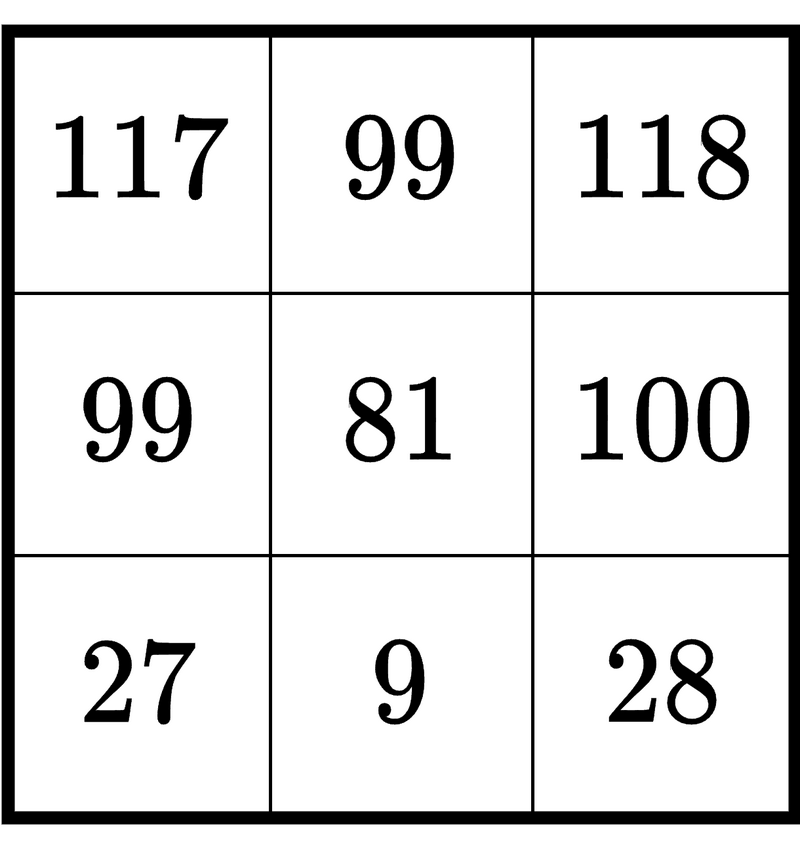
例えば，葵さんは上から 1 行目，左から 1 列目のマスには A_1 + B_1 = 97 + 20 = 117 を書く．また，上から 3 行目，左から 2 列目のマスには A_3 + B_2 = 7 + 2 = 9 を書く．

葵さんが書く 9 個の整数は 117, 99, 118, 99, 81, 100, 27, 9, 28 であり，それぞれの桁数は 3, 2, 3, 2, 2, 3, 2, 1, 2 である．

よって，葵さんが書く 9 個の整数の桁数の合計は 3 + 2 + 3 + 2 + 2 + 3 + 2 + 1 + 2 = 20 となるため，20 を出力する．

この入力例は小課題 2, 3, 8 の制約を満たす．

入力例 2

4
8 97 996 9995
1 2 3 4

出力例 2

葵さんが各マスに書く数字は以下の図のようになる．

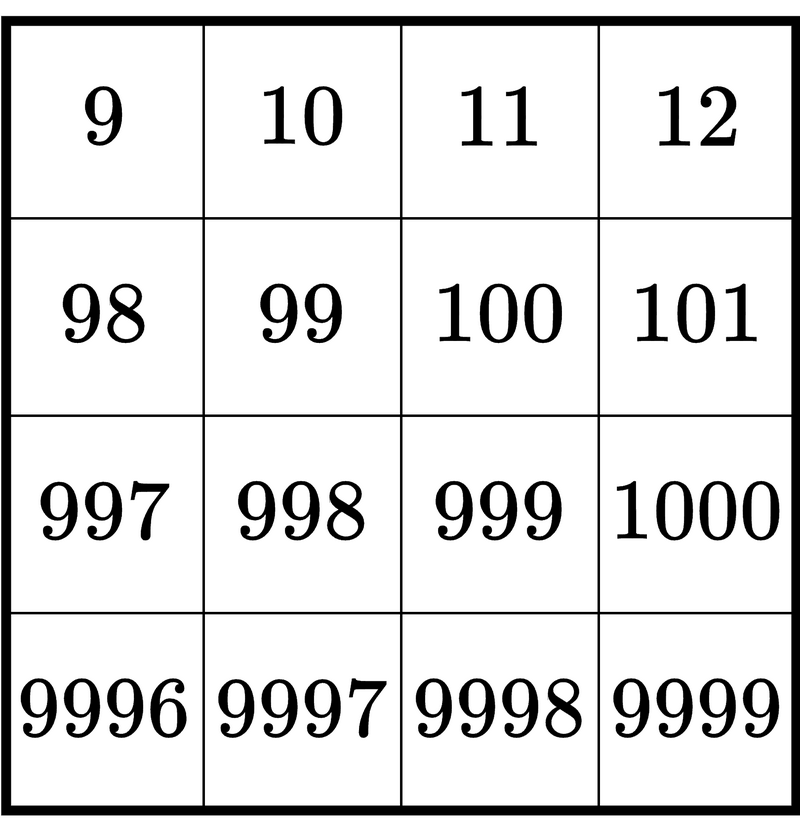
例えば，葵さんは上から 2 行目，左から 3 列目のマスには A_2 + B_3 = 97 + 3 = 100 を書く．この整数の桁数は 3 である．また，上から 4 行目，左から 2 列目のマスには A_4 + B_2 = 9\,995 + 2 = 9\,997 を書く．この整数の桁数は 4 である．

葵さんが書く 16 個の整数の桁数の合計は 46 となるため，46 を出力する．

この入力例は小課題 2, 6, 7, 8 の制約を満たす．

入力例 3

1
500000000
500000000

出力例 3

葵さんが書く整数は 1 個で，その値は 500\,000\,000 + 500\,000\,000 = 1\,000\,000\,000 である．この整数の桁数は 10 である．

よって，葵さんが書く 1 個の整数の桁数の合計は 10 となるため，10 を出力する．

この入力例は小課題 1, 2, 4, 5, 8 の制約を満たす．

入力例 4

7
436981378 523812834 456708479 413571178 506402783 598271009 523936624
401203104 501634329 506090236 527167431 485527116 439442403 568364549

出力例 4

この入力例は小課題 2, 5, 8 の制約を満たす．

E - 名前 (Name)

Time Limit: 1 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 君と IOI 君は犬を飼うことにした．最初にすべきことは，犬の名前を決めることである．二人で話し合った結果，犬の名前を以下の 4 つの条件を満たすものにすることにした．

条件 1　名前は英大文字 (A, B, ..., Z) と英小文字 (a, b, ..., z) からなる文字列である．

条件 2　JOI 君の好きな文字列は長さ N の文字列 S であるから，S が名前の部分列となるようにする．

条件 3　IOI 君の好きな文字列は長さ M の文字列 T であるから，T が名前の部分列となるようにする．

条件 4　名前を呼びやすいものにするため，同じ文字の間には別の文字が K 文字以上あるようにする．厳密には，位置が異なる任意の同じ文字 2 つについて，必ずその間に別の文字が K 文字以上入っているようにする．なお，K = 0 の場合や，名前の文字がすべて異なる場合は，この条件を満たしていると考える．

ただし，これらの条件では英大文字と英小文字は区別される．例えば A と a は異なる文字とみなされることに注意せよ．

ここで，名前の部分列とは，名前から何文字か (0 文字でもよい) を取り除いて作れる文字列のことである．例えば，名前が algorithm であるとき，ai や lgtm は名前の部分列であるが，joi や logarithm は名前の部分列ではない．

二人は名前が短いほど良いと考えているため，4 つの条件のもとで最も短い名前を付けることにした．

JOI 君と IOI 君の好きな文字列および整数 K が与えられたとき，犬に付ける名前の文字数を求めるプログラムを作成せよ．

制約

1 \leqq N \leqq 500．
1 \leqq M \leqq 500．
0 \leqq K \leqq 3．
S は英大文字と英小文字からなる長さ N の文字列である．
T は英大文字と英小文字からなる長さ M の文字列である．
N, M, K は整数である．

小課題

(2 点) S = T，K = 0．
(7 点) S = T，K = 1．
(16 点) S = T．
(17 点) K = 0．
(13 点) K = 1，N \leqq 25，M \leqq 25．
(15 点) K = 1．
(20 点) K \leqq 2．
(10 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N M K
S
T

出力

犬に付ける名前の文字数を 1 行で出力せよ．

入力例 1

10 10 0
hottokeiki
hottokeiki

出力例 1

JOI 君と IOI 君の好きな文字列はどちらも hottokeiki である．ここで，犬の名前を hottokeiki にすることを考える．これは以下のように 4 つの条件を満たす．

条件 1: 名前は英大文字と英小文字からなる．
条件 2: 文字列 S (hottokeiki) は犬の名前 hottokeiki の部分列である．
条件 3: 文字列 T (hottokeiki) は犬の名前 hottokeiki の部分列である．
条件 4: K = 0 なので，この条件は満たしている．

また，これが 4 つの条件を満たす中で最も短い名前である．この文字数 10 を出力する．

この入力例は小課題 1, 3, 4, 7, 8 の制約を満たす．

入力例 2

10 10 1
hottokeiki
hottokeiki

出力例 2

入力例 1 とは K の値のみが異なる．

もし犬の名前を入力例 1 と同じ hottokeiki にすれば，条件 4 を満たさない．なぜなら，2 つの t の間に文字が 1 個もないからである．

4 つの条件を満たす最も短い名前として hotNtokeiki などが考えられる．この文字数 11 を出力する．

この入力例は小課題 2, 3, 5, 6, 7, 8 の制約を満たす．

入力例 3

10 10 3
hottokeiki
hottokeiki

出力例 3

入力例 1, 2 とは K の値のみが異なる．

もし犬の名前を入力例 2 と同じ hotNtokeiki にすれば，条件 4 を満たさない．なぜなら，2 つの t の間に 1 文字しかなく，2 つの k の間に 2 文字しかなく，2 つの i の間に 1 文字しかないからである．

4 つの条件を満たす最も短い名前として hotarutokeiyuki などが考えられる．この文字数 15 を出力する．

この入力例は小課題 3, 8 の制約を満たす．

入力例 4

6 9 0
Jouhou
Orinpikku

出力例 4

JOI 君の好きな文字列は Jouhou，IOI 君の好きな文字列は Orinpikku である．ここで，犬の名前を OJouhorinpikku にすることを考える．これは以下のように 4 つの条件を満たす．

条件 1: 名前は英大文字と英小文字からなる．
条件 2: 文字列 S (Jouhou) は犬の名前 OJouhorinpikku の部分列である．
条件 3: 文字列 T (Orinpikku) は犬の名前 OJouhorinpikku の部分列である．
条件 4: K = 0 なので，この条件は満たしている．

また，これが 4 つの条件を満たす中で最も短い名前のひとつである．この文字数 14 を出力する．なお，英大文字と英小文字は区別されるため，jouhorinpikku（文字数 13）などは条件を満たさない．

この入力例は小課題 4, 7, 8 の制約を満たす．

入力例 5

9 7 1
CoMMiTTee
TeRRaCe

出力例 5

4 つの条件を満たす最も短い名前として CoMaMiTeRTeRaCe などが考えられる．この文字数 15 を出力する．

この入力例は小課題 5, 6, 7, 8 の制約を満たす．

入力例 6

6 8 2
JOIIOI
JOIGEGOI

出力例 6

4 つの条件を満たす最も短い名前は JOIGEIGOI である．この文字数 9 を出力する．

この入力例は小課題 7, 8 の制約を満たす．

F - 感染シミュレーション (Infection Simulation)

Time Limit: 1.5 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

EGOI 食堂には昨日 N 人の客が来店した．客には 1 から N までの番号が付けられており，客 i (1 \leqq i \leqq N) の来店時刻は L_i，退店時刻は R_i であった．そして今日，客のうち 1 人が，現在 JOI 国で流行している新型の感染症 X に感染した状態で来店したことが明らかになった．

感染症 X の感染しづらさは整数 x で表される．具体的には，1 \leqq i \leqq N について，客 i が 1 人以上の感染者と同時に食堂内にいた時間の累計が x 以上となったタイミングで，客 i は新たに感染者となる．

さて，JOI 国では厳格な感染症対策を行っているため，感染者数を正確に把握しなければならない．しかし困ったことに，誰が感染症 X に感染したかの情報は得られておらず，感染しづらさを表す整数 x も分かっていない．

そこで EGOI 食堂の店長である理恵さんは，Q 個のシナリオについて，最終的に何人の客が感染するのかを求めることにした． j 番目 (1 \leqq j \leqq Q) のシナリオでは，最初の感染者が客 P_j のみであり，感染症 X の感染しづらさが X_j である．

来店した客およびシナリオの情報が与えられたとき，それぞれのシナリオにおける最終的な感染者数を出力するプログラムを作成せよ．ただし，退店時刻ちょうどに感染した場合も，感染者数に含めるものとする．また，感染症 X に一度感染した客が感染者でなくなることは考えないものとする．

制約

1 \leqq N \leqq 100\,000．
0 \leqq L_i < R_i \leqq 10^9 (1 \leqq i \leqq N)．
1 \leqq Q \leqq 100\,000．
1 \leqq P_j \leqq N (1 \leqq j \leqq Q)．
1 \leqq X_j \leqq 10^9 (1 \leqq j \leqq Q)．
入力される値はすべて整数である．

小課題

(2 点) L_i = 0 (1 \leqq i \leqq N)，R_i = 10 (1 \leqq i \leqq N)，Q \leqq 5．
(3 点) L_i = 0 (1 \leqq i \leqq N)，Q \leqq 5．
(6 点) L_i = 0 (1 \leqq i \leqq N)．
(10 点) N \leqq 500，Q \leqq 5，R_i \leqq 500 (1 \leqq i \leqq N)，X_j \leqq 500 (1 \leqq j \leqq Q)．
(11 点) N \leqq 500，Q \leqq 5．
(16 点) Q \leqq 5．
(13 点) P_j = 1 (1 \leqq j \leqq Q)，L_1 < L_2 < \cdots < L_N，R_1 < R_2 < \cdots < R_N．
(14 点) P_j = 1 (1 \leqq j \leqq Q)．
(15 点) R_i - L_i (1 \leqq i \leqq N) の最小値は，X_j (1 \leqq j \leqq Q) の最大値以上である．
(10 点) 追加の制約はない．

入力

入力は以下の形式で与えられる．

N
L_1 R_1
L_2 R_2
\vdots
L_N R_N
Q
P_1 X_1
P_2 X_2
\vdots
P_Q X_Q

出力

Q 行出力せよ．j 行目 (1 \leqq j \leqq Q) には，j 番目のシナリオにおける最終的な感染者数を出力せよ．

入力例 1

出力例 1

1 番目のシナリオでは，最初の感染者が客 1，感染症 X の感染しづらさが 15 であるため，以下のようにして感染が広がる．

時刻 10 に客 1 が来店する．
時刻 20 に客 2 が来店する．
時刻 35 に客 2 が 1 人以上の感染者と同時に食堂内にいた時間の累計が 15 となり，客 2 が感染する．
時刻 40 に客 1 が退店する．
時刻 45 に客 3 が来店する．
時刻 60 に客 3 が 1 人以上の感染者と同時に食堂内にいた時間の累計が 15 となり，客 3 が感染する．同時に，客 3 が退店する．
時刻 70 に客 4 が来店する．
時刻 80 に客 2 が退店する．
時刻 95 に客 4 が退店する．客 4 が 1 人以上の感染者と同時に食堂内にいたのは時刻 70 から時刻 80 までであり，時間の累計は 10 であるため，客 4 は感染しない．

最終的に客 1, 2, 3 の 3 人が感染するため，1 行目には 3 を出力する．

この入力例は小課題 4, 5, 6, 8, 9, 10 の制約を満たす．

入力例 2

出力例 2

7
1
5

1 番目のシナリオでは，最終的に客 1, 2, 3, 4, 6, 7, 8 の 7 人が感染するため，1 行目には 7 を出力する．

2 番目のシナリオでは，最終的に客 1 の 1 人が感染するため，2 行目には 1 を出力する．

3 番目のシナリオでは，最終的に客 2, 3, 4, 7, 8 の 5 人が感染するため，3 行目には 5 を出力する．

この入力例は小課題 2, 3, 4, 5, 6, 10 の制約を満たす．

入力例 3

5
0 10
0 10
0 10
0 10
0 10
4
1 9
1 10
1 11
1 1000000000

出力例 3

この入力例は小課題 1, 2, 3, 5, 6, 8, 10 の制約を満たす．

入力例 4

出力例 4

この入力例は小課題 4, 5, 6, 9, 10 の制約を満たす．

入力例 5

出力例 5

この入力例は小課題 4, 5, 6, 7, 8, 9, 10 の制約を満たす．

入力例 6

出力例 6

この入力例は小課題 4, 5, 6, 8, 10 の制約を満たす．

入力例 7

出力例 7

この入力例は小課題 4, 5, 6, 9, 10 の制約を満たす．