Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
JOI 高校の生徒である葵は,文字列 JOIG が,文字列 JOI の末尾に文字 G を付け加えてできることに気が付いた.
そこから葵は,様々な文字列について,末尾に文字 G を付け加えたり,末尾の文字 G を取り除いて遊ぶようになった.
具体的には,葵は文字列を見ると次のように遊ぶ.
- 見た文字列の末尾の文字が
Gのとき,末尾の文字Gを取り除いた文字列を思い浮かべる.取り除く文字は末尾の 1 文字のみである. - 見た文字列の末尾の文字が
Gでないとき,文字列の末尾に文字Gを付け加えた文字列を思い浮かべる.
長さ N の文字列 S が与えられる.葵が文字列 S を見たとき思い浮かべる文字列を求めるプログラムを作成せよ.
制約
- 2 \leqq N \leqq 100.
- S は長さ N の文字列である.
- S の各文字は英大文字である.
- N は整数である.
入力
入力は以下の形式で与えられる.
N S
出力
葵が文字列 S を見たとき思い浮かべる文字列を出力せよ.
入力例 1
4 JOIG
出力例 1
JOI
葵が見た文字列 JOIG の末尾の文字は G であるから,葵は末尾の文字 G を取り除いた文字列 JOI を思い浮かべる.そのため,JOI を出力する.
入力例 2
3 JOI
出力例 2
JOIG
葵が見た文字列 JOI の末尾の文字は G でないので,葵は末尾に文字 G を付け加えた文字列 JOIG を思い浮かべる.そのため,JOIG を出力する.
入力例 3
3 EGG
出力例 3
EG
葵が見た文字列 EGG の末尾の文字は G であるから,葵は末尾の文字 G を取り除いた文字列 EG を思い浮かべる.そのため,EG を出力する.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
JOI 高校の葵さんは,数列に対して,隣り合う各項の差の絶対値を順に並べた数列を考えるのが好きである.
はじめ,黒板には長さ N の数列 A_1,A_2,\ldots,A_N が書かれている.
葵さんは以下の操作を N-1 回繰り返す.
- 黒板に書かれている数列の長さが m であり,その数列が b_1,b_2,\ldots,b_m であるとする. 黒板に書かれている数列 b_1,b_2,\ldots,b_m を消し,長さ m-1 の数列 |b_1-b_2|,|b_2-b_3|,\ldots,|b_{m-1}-b_m| を新たに黒板に書く.ただし,|x| は x の絶対値を表す.
N-1 回の操作が終了した後,黒板には 1 つの値(長さ 1 の数列)が書かれている.
はじめ黒板に書かれていた数列の情報が与えられるので,N-1 回の操作が終了した後黒板に書かれている値を求めるプログラムを作成せよ.
制約
- 2 \leqq N \leqq 2\,000.
- 0 \leqq A_i \leqq 10^9.
- 入力される値はすべて整数である.
小課題
- (25 点) N=2.
- (75 点) 追加の制約はない.
入力
入力は以下の形式で与えられる.
N A_1 A_2 \cdots A_N
出力
N-1 回の操作が終了した後黒板に書かれている値を出力せよ.
入力例 1
4 3 1 4 1
出力例 1
1
はじめ黒板には長さ 4 の数列 3,1,4,1 が書かれている.
葵は (4-1=)3 回の操作を行う.
- 1 回目の操作では,黒板から長さ 4 の数列 3,1,4,1 を消し,長さ 3 の数列 2,3,3 を書く.
- 2 回目の操作では,黒板から長さ 3 の数列 2,3,3 を消し,長さ 2 の数列 1,0 を書く.
- 3 回目の操作では,黒板から長さ 2 の数列 1,0 を消し,長さ 1 の数列 1 を書く.
3 回の操作が終了した後に黒板に書かれている値は 1 であるので,1 を出力する.
この入力例は小課題 2 の制約を満たす.
入力例 2
2 2 4
出力例 2
2
この入力例はすべての小課題の制約を満たす.
入力例 3
6 2 7 5 3 3 11
出力例 3
3
この入力例は小課題 2 の制約を満たす.
入力例 4
10 3 1 4 1 5 9 2 6 5 3
出力例 4
0
この入力例は小課題 2 の制約を満たす.
入力例 5
2 0 0
出力例 5
0
この入力例はすべての小課題の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
JOI 市には 1 本の十分に長い道路がある.この道路は数直線とみなすことができ,各地点は 1 個の実数による座標で表される.
また,JOI 市にはこの道路に沿って N 個の鐘があり,座標の小さい順に 1 から N までの番号が付けられている.鐘 i (1 ≦ i ≦ N) は座標 A_i にある.
JOI 市では,1 年の終わりにこれらの鐘を一斉に鳴らすのが一大イベントとなっている.
どの鐘も,鳴らすとその鐘と同じ地点では強さ K の音で聞こえるが,距離が 1 離れるごとに聞こえる音の強さは 1 小さくなり,距離が K 以上離れると 0 になる.すなわち,鐘 i を鳴らしたとき,座標 x で聞こえる鐘 i の音の強さは \max\{K - |x - A_i|, 0\} である.ただし,|t| は t の絶対値を表す.
すべての鐘を鳴らしたとき,座標 x で聞こえる鐘の音の強さは,座標 x で聞こえるそれぞれの鐘の音の強さの最大値である.
JOI 市にはこの道路に沿って M 個の家があり,古い方から順に 1 から M までの番号が付けられている.家 j (1 ≦ j ≦ M) は座標 B_j にある.
JOI 市の市長であるあなたは,すべての鐘を鳴らしたとき,それぞれの家で聞こえる鐘の音の強さを知りたい.
JOI 市の鐘と家の情報が与えられたとき,すべての鐘を鳴らしたときに座標 B_1, B_2, …, B_M で聞こえる鐘の音の強さを求めるプログラムを作成せよ.
制約
- 1 \leqq N \leqq 250\,000.
- 1 \leqq M \leqq 250\,000.
- 1 \leqq K \leqq 10^9.
- 0 \leqq A_i \leqq 10^9 (1 \leqq i \leqq N).
- A_i \lt A_{i+1} (1 \leqq i \leqq N - 1).
- 0 \leqq B_j \leqq 10^9 (1 \leqq j \leqq M).
- B_j ≠ B_k (1 \leqq j < k \leqq M).
- 入力される値はすべて整数である.
小課題
- (20 点) N = 1,M \leqq 1\,000.
- (20 点) N \leqq 1\,000,M \leqq 1\,000.
- (60 点) 追加の制約はない.
入力
入力は以下の形式で与えられる.
N M K A_1 A_2 \cdots A_N B_1 B_2 \cdots B_M
出力
M 行出力せよ.j 行目 (1 \leqq j \leqq M) には,すべての鐘を鳴らしたときに座標 B_j で聞こえる鐘の音の強さを出力せよ.
入力例 1
1 5 10 20 20 15 28 10 32
出力例 1
10 5 2 0 0
この入力例では,座標 20 に鐘 1 がある.
- 鐘 1 を鳴らしたとき,座標 20 で聞こえる鐘 1 の音の強さは \max\{10 - |20 - 20|, 0\} = 10 である.したがって,1 行目には 10 を出力する.
- 鐘 1 を鳴らしたとき,座標 15 で聞こえる鐘 1 の音の強さは \max\{10 - |15 - 20|, 0\} = 5 である.したがって,2 行目には 5 を出力する.
- 鐘 1 を鳴らしたとき,座標 28 で聞こえる鐘 1 の音の強さは \max\{10 - |28 - 20|, 0\} = 2 である.したがって,3 行目には 2 を出力する.
- 鐘 1 を鳴らしたとき,座標 10 で聞こえる鐘 1 の音の強さは \max\{10 - |10 - 20|, 0\} = 0 である.したがって,4 行目には 0 を出力する.
- 鐘 1 を鳴らしたとき,座標 32 で聞こえる鐘 1 の音の強さは \max\{10 - |32 - 20|, 0\} = 0 である.したがって,5 行目には 0 を出力する.
この入力例はすべての小課題の制約を満たす.
入力例 2
3 4 100 116 194 258 57 155 222 360
出力例 2
41 61 72 0
- 鐘 1,2,3 を鳴らしたとき,座標 57 で聞こえる音の強さはそれぞれ 41,0,0 である.したがって,すべての鐘を鳴らしたときに座標 57 で聞こえる音の強さはこれらの最大値である 41 である.そのため,1 行目には 41 を出力する.
- 鐘 1,2,3 を鳴らしたとき,座標 155 で聞こえる音の強さはそれぞれ 61,61,0 である.したがって,すべての鐘を鳴らしたときに座標 155 で聞こえる音の強さはこれらの最大値である 61 である.そのため,2 行目には 61 を出力する.
- 鐘 1,2,3 を鳴らしたとき,座標 222 で聞こえる音の強さはそれぞれ 0,72,64 である.したがって,すべての鐘を鳴らしたときに座標 222 で聞こえる音の強さはこれらの最大値である 72 である.そのため,3 行目には 72 を出力する.
- 鐘 1,2,3 を鳴らしたとき,座標 360 で聞こえる音の強さはそれぞれ 0,0,0 である.したがって,すべての鐘を鳴らしたときに座標 360 で聞こえる音の強さはこれらの最大値である 0 である.そのため,4 行目には 0 を出力する.
この入力例は小課題 2, 3 の制約を満たす.
入力例 3
10 10 10000 589 2398 6567 28817 29177 31636 45468 66751 82282 97509 2196 54498 80474 61644 18007 38759 85590 72172 79533 69959
出力例 3
9798 970 8192 4893 0 3291 6692 4579 7251 6792
この入力例は小課題 2, 3 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
机の上に,縦 H 行,横 W 列の長方形状にコインが並べられている.
最初,上から i 行目 (1 \leqq i \leqq H),左から j 列目 (1 \leqq j \leqq W) のコインは,
S_{i,j}= # のとき表面,S_{i,j}= . のとき裏面が見えている状態である.
葵と凛は,これらのコインを用いてゲームを行うことにした.ゲームは以下のような流れで行われる.
- 葵がどれか 1 つの行を選び,その行のコインをすべてひっくり返す.
- 凛がどれか 1 つの列を選び,その列のコインをすべてひっくり返す.
- 葵が,表面が見えるコインをすべて獲得する.また凛が,裏面が見えるコインをすべて獲得する.
葵と凛はそれぞれ,できるだけ多くのコインを獲得したい.
ゲーム開始時のコインの状態が与えられたとき, 両者が最善を尽くした場合にそれぞれが獲得できるコインの枚数を求めるプログラムを作成せよ.
制約
- H \geqq 1.
- W \geqq 1.
- H \times W \leqq 500\,000.
- S_{i, j} は
#,.のいずれかである (1 \leqq i \leqq H,1 \leqq j \leqq W). - H, W は整数である.
小課題
- (2 点) H = 1,W = 1.
- (8 点) H = 1,W \leqq 40.
- (9 点) H \leqq 40,W = 1.
- (14 点) H = 2,W = 2.
- (23 点) H \leqq 40,W \leqq 40.
- (18 点) H \leqq 250,W \leqq 250.
- (26 点) 追加の制約はない.
入力
入力は以下の形式で与えられる.
H W
S_{1,1}S_{1,2}\cdotsS_{1,W}
S_{2,1}S_{2,2}\cdotsS_{2,W}
\vdots
S_{H,1}S_{H,2}\cdotsS_{H,W}
出力
葵と凛の得点をこの順に空白区切りで出力せよ.
入力例 1
1 1 #
出力例 1
1 0
この入力例では,必ず以下のようにゲームが進行する.
- まず,葵が 1 行目のすべてのコインをひっくり返す.
- 次に,凛が 1 列目のすべてのコインをひっくり返す.
このとき,唯一のコインの見える面は「表→裏→表」と変化するため,葵が 1 枚のコインを獲得できるが,凛はコインを獲得できない.したがって,1,0 をこの順に空白区切りで出力する.
なお,この入力例は小課題 1, 2, 3, 5, 6, 7 の制約を満たす.
入力例 2
5 5 ##### ####. ###.. ##... #....
出力例 2
13 12
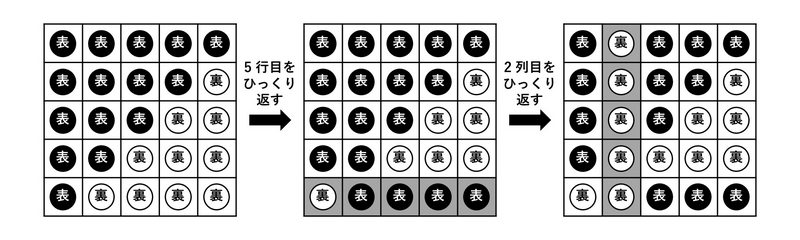
両者が最善を尽くした場合の,ゲームの進行の一例を下図に示す.
この入力例は小課題 5, 6, 7 の制約を満たす.
入力例 3
1 40 ..........##########..........##########
出力例 3
19 21
この入力例は小課題 2, 5, 6, 7 の制約を満たす.
入力例 4
7 1 # # # # # # #
出力例 4
1 6
この入力例は小課題 3, 5, 6, 7 の制約を満たす.
入力例 5
5 5 .###. ...## ..##. .##.. ##...
出力例 5
11 14
この入力例は小課題 5, 6, 7 の制約を満たす.
入力例 6
10 40 ........................................ ..######.....####.....#####.....####.... .....#......#....#......#......#........ .....#......#....#......#......#........ .....#......#....#......#......#........ .....#......#....#......#......#..####.. ..#..#......#....#......#......#....#... ..#..#......#....#......#......#....#... ...##........####.....#####.....####.... ........................................
出力例 6
104 296
この入力例は小課題 5, 6, 7 の制約を満たす.
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
JOIG 王国は H 行 W 列のマス目に区切られた長方形の形をしている.上から i 行目 (1 \leqq i \leqq H),左から j 列目 (1 \leqq j \leqq W) のマスをマス (i,j) と呼ぶ.
各マスには標高と呼ばれる整数が定まっている.マス (i,j) の標高は A_{i,j} である.
JOIG 王国では,王国を縦断する運河を建設することにした.運河の建設は,以下のように行われる.
- ある整数 k (1 \leqq k < W) を定める.左から k 列目と k+1 列目の間に,王国の上端から下端まで縦断する運河を建設する.
運河を横切らず,辺で接している標高が同じマスへの移動を繰り返すことで相互に移動できるマスの集まりをここでは平地と呼ぶ.国土を管理しやすくするため,平地の個数ができるだけ少なくなるように運河の建設位置を決めたい.
JOIG 王国の地形の情報が与えられたとき,運河を建設した後の JOIG 王国内の平地の個数としてありうる最小値を求めるプログラムを作成せよ.
制約
- H \geqq 1.
- W \geqq 2.
- H \times W \leqq 500\,000.
- 1 \leqq A_{i,j} \leqq 10^9 (1 \leqq i \leqq H,1 \leqq j \leqq W).
- 入力される値はすべて整数である.
小課題
- (6 点) H = 1.
- (20 点) H \leqq 2.
- (27 点) H \leqq 200,W \leqq 200.
- (47 点) 追加の制約はない.
入力
入力は以下の形式で与えられる.
H W
A_{1,1} A_{1,2} \cdots A_{1,W}
A_{2,1} A_{2,2} \cdots A_{2,W}
\vdots
A_{H,1} A_{H,2} \cdots A_{H,W}
出力
運河を建設した後の JOIG 王国内の平地の個数としてありうる最小値を出力せよ.
入力例 1
4 4 1 1 1 3 2 2 1 3 2 1 1 3 2 2 2 2
出力例 1
4
k=3 として運河を建設すると,JOIG 王国は以下のように 4 個の平地に分かれる.
- マス (1,1),(1,2),(1,3),(2,3),(3,2),(3,3) からなる平地
- マス (2,1),(2,2),(3,1),(4,1),(4,2),(4,3) からなる平地
- マス (1,4),(2,4),(3,4) からなる平地
- マス (4,4) からなる平地
JOIG 王国内の平地の個数を 3 個以下にすることはできないので,4 を出力する.
この入力は小課題 3, 4 の制約を満たす.
入力例 2
5 8 1 2 2 5 5 5 5 5 1 1 2 2 5 6 5 6 1 1 1 1 6 6 5 6 1 1 3 1 1 6 7 6 1 4 1 1 1 6 6 6
出力例 2
8
k=1 として運河を建設すると,JOIG 王国は 8 個の平地に分かれる.JOIG 王国内の平地の個数を 7 個以下にすることはできないので,8 を出力する.
この入力は小課題 3, 4 の制約を満たす.
入力例 3
1 6 1 1 2 2 3 3
出力例 3
3
この入力はすべての小課題の制約を満たす.
入力例 4
2 10 1 1 1 1 1 3 3 3 3 4 1 2 1 3 3 3 1 1 3 3
出力例 4
6
この入力は小課題 2, 3, 4 の制約を満たす.
Time Limit: 2.5 sec / Memory Limit: 1024 MiB
配点: 100 点
問題文
JOIG 国では JOIG 語が使用されており,JOIG 語では文字 A, B, C, D, E, F, G, H, I, J, K, L, M, N, O の 15 種類の文字が用いられる.
来月 JOIG 国で開催されるタイピング大会では,JOIG 語で用いられる 15 種類の文字からなる長さ N の文字列 S を入力するのにかかる時間を競う.この大会では,参加者は以下の条件でタイピングを行う.
- 参加者は,1 本の指を使ってタイピングをする.
- 参加者は,15 種類の文字のキー 1 つずつを 1 列に並べた,左右に細長いキーボードを使用する.なお,どの位置にどの文字のキーを配置するかは,各参加者が自由に決めることができる.
- 参加者は,文字列 S の 1, 2, \dots, N 文字目のキーをこの順に打つことによって文字列 S を入力する.
この大会には Q 人が参加する予定である.参加者によってタイピングの能力は様々である.i 番目 (1 \leqq i \leqq Q) の参加者は,タイピングに際して以下のような時間がかかる.
- 指の真下にあるキーを 1 回打つのに A_i ミリ秒かかる.
- 指を 1 つ左のキーの上に移動させるのに L_i ミリ秒かかる.
- 指を 1 つ右のキーの上に移動させるのに R_i ミリ秒かかる.
文字列 S および各参加者の情報が与えられるので,各参加者に対して,文字列 S の最初の文字を打ち始めてから最後の文字を打ち終わるまでに最短何ミリ秒かかるかを求めるプログラムを作成せよ.
制約
- 1 \leqq N \leqq 1\,000\,000.
- S は長さ N の文字列である.
- S の各文字は
A,B,C,D,E,F,G,H,I,J,K,L,M,N,Oのいずれかである. - 1 \leqq Q \leqq 150\,000.
- 1 \leqq A_i \leqq 10^{11} (1 \leqq i \leqq Q).
- 1 \leqq L_i \leqq 10^{11} (1 \leqq i \leqq Q).
- 1 \leqq R_i \leqq 10^{11} (1 \leqq i \leqq Q).
- N, Q, A_i, L_i, R_i は整数である.
小課題
- (2 点) S の各文字は
Aである,Q = 1. - (3 点) S の各文字は
A,Bのいずれかである,Q = 1. - (4 点) S の各文字は
A,B,Cのいずれかである,Q = 1. - (9 点) S の各文字は
A,B,C,D,E,F,G,Hのいずれかである,Q = 1,N \leqq 100. - (14 点) S の各文字は
A,B,C,D,E,F,G,Hのいずれかである,Q = 1. - (26 点) S の各文字は
A,B,C,D,E,F,G,Hのいずれかである. - (23 点) Q = 1.
- (7 点) L_i = R_i (1 \leqq i \leqq Q).
- (12 点) 追加の制約はない.
入力
入力は以下の形式で与えられる.
N S Q A_1 L_1 R_1 A_2 L_2 R_2 \vdots A_Q L_Q R_Q
出力
Q 行出力せよ.i 行目 (1 \leqq i \leqq Q) には,参加者 i が文字列 S の最初の文字を打ち始めてから最後の文字を打ち終わるまでに最短何ミリ秒かかるかを出力せよ.
入力例 1
6 ABAABB 1 100 150 210
出力例 1
1110
例えば,キーボードの配列を左から順に ONMLKJIHGFEDCBA とすることを考える.このとき,以下の表のような動作を行うことで, 1\,110 ミリ秒で文字列 ABAABB を入力できる.
| 手順 | 動作 | 指の真下にあるキー | 時間(ミリ秒) |
|---|---|---|---|
| 1 | A のキーを打つ | A | 100 |
| 2 | 指を 1 つ左のキーの上に移動させる | A → B | 150 |
| 3 | B のキーを打つ | B | 100 |
| 4 | 指を 1 つ右のキーの上に移動させる | B → A | 210 |
| 5 | A のキーを打つ | A | 100 |
| 6 | A のキーを打つ | A | 100 |
| 7 | 指を 1 つ左のキーの上に移動させる | A → B | 150 |
| 8 | B のキーを打つ | B | 100 |
| 9 | B のキーを打つ | B | 100 |
上に挙げたキーボードの配列以外にも,文字列 ABAABB を同じ時間で入力できるものはあるが,より短い時間で入力することはできない.よって 1\,110 を出力する.
この入力例は小課題 2, 3, 4, 5, 6, 7, 9 の制約を満たす.
入力例 2
6 CBACAB 1 150 240 220
出力例 2
2260
例えば,キーボードの配列を左から順に CABDEFGHIJKLMNO とすることを考える.このとき,以下の表のような動作を行うことで,2\,260 ミリ秒で文字列 CBACAB を入力できる.
| 手順 | 動作 | 指の真下にあるキー | 時間(ミリ秒) |
|---|---|---|---|
| 1 | C のキーを打つ | C | 150 |
| 2 | 指を 1 つ右のキーの上に移動させる | C → A | 220 |
| 3 | 指を 1 つ右のキーの上に移動させる | A → B | 220 |
| 4 | B のキーを打つ | B | 150 |
| 5 | 指を 1 つ左のキーの上に移動させる | B → A | 240 |
| 6 | A のキーを打つ | A | 150 |
| 7 | 指を 1 つ左のキーの上に移動させる | A → C | 240 |
| 8 | C のキーを打つ | C | 150 |
| 9 | 指を 1 つ右のキーの上に移動させる | C → A | 220 |
| 10 | A のキーを打つ | A | 150 |
| 11 | 指を 1 つ右のキーの上に移動させる | A → B | 220 |
| 12 | B のキーを打つ | B | 150 |
上に挙げたキーボードの配列以外でも,文字列 CBACAB を同じ時間で入力できるものはあるが,より短い時間で入力することはできない.よって 2\,260 を出力する.
この入力例は小課題 3, 4, 5, 6, 7, 9 の制約を満たす.
入力例 3
20 AAAAAAAAAAAAAAAAAAAA 1 230000000 80000000 80000000
出力例 3
4600000000
A を 20 回打つことになるので,キーボードの配列にかかわらず,入力し終わるまでに最短で 230\,000\,000 \times 20 = 4\,600\,000\,000 ミリ秒かかる.よって 4\,600\,000\,000 を出力する.
この入力例はすべての小課題の制約を満たす.
入力例 4
7 EACHBAG 5 130 104 162 107 219 45 144 168 157 213 79 257 100000000000 100000000000 100000000000
出力例 4
2078 1766 2465 2894 1600000000000
この入力例は小課題 6, 9 の制約を満たす.
入力例 5
19 JOIGCODINGCHALLENGE 5 1 1 1 100 200 200 225 111 111 123456789 987654321 987654321 31415926535 27182818284 27182818284
出力例 5
48 7700 7494 30987654300 1385204334401
この入力例は小課題 8, 9 の制約を満たす.