A - 図書館 2 (Library 2)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

読書好きのビ太郎は図書館で本を借りて読むことにした．ビ太郎の家は狭いため，床には本 1 冊分の広さのスペースしかない．ただし高さは十分にあるため，ビ太郎はこのスペースに本を積んで管理することにした．

ビ太郎はこれから Q 回の行動を取る．i (1 \leqq i \leqq Q) 回目の行動は文字列 S_i で表される．S_i は 英小文字からなる文字列か READ のいずれかであり，その意味は次の通りである．

  • 英小文字からなる文字列の場合，ビ太郎は書名が S_i である本を図書館から借り，スペースの一番上に積む．
  • READ の場合，ビ太郎はスペースの一番上に積まれている本を読み，図書館に返却する．

あなたはビ太郎がどの本をどのような順番で読んだのかを調べたい．

Q 回の行動の内容が与えられたとき，ビ太郎が読んだ本の書名を読んだ順に出力するプログラムを作成せよ．

制約

  • 2 \leqq Q \leqq 200\,000．
  • Q は整数である．
  • S_i は長さ 1 以上 10 以下の文字列である (1 \leqq i \leqq Q)．
  • S_i は英小文字からなる文字列または READ である (1 \leqq i \leqq Q)．
  • S_i が READ であるような i (1 \leqq i \leqq Q) は 1 つ以上存在する．
  • S_i が READ のとき，必ずスペースに 1 冊以上の本が存在する (1 \leqq i \leqq Q) ．

小課題

  1. (40 点) Q \leqq 2\,000．
  2. (60 点) 追加の制約はない．

採点に関する注意

すべての提出はジャッジシステム上で採点される．

提出されたソースコードは，小課題に対応するすべての採点用入力データについて正しい結果を返したとき，その小課題について正解と認められる．

各提出の得点は，提出されたソースコードについて正解と認められた小課題の得点の合計である．

この課題の得点は，この課題に対するすべての提出の得点の最大値である．

現在の得点は「提出結果」タブの「自分の得点状況」から確認できる．

入力

入力は以下の形式で標準入力から与えられる．

Q
S_1
S_2
\vdots
S_Q

出力

標準出力に，S_i が READ である行動のそれぞれに対して，ビ太郎が読んだ本の書名を順に改行区切りで出力せよ．

入力例 1

7
joi
joig
ioi
READ
egoi
READ
READ

出力例 1

ioi
egoi
joig

この入力例ではビ太郎は以下のように行動する．

  1. 書名が joi である本をスペースに積む．このとき，スペースに積まれている本の書名は joi となる．
  2. 書名が joig である本をスペースに積む．このとき，スペースに積まれている本の書名は上から順に joig ，joi となる．
  3. 書名が ioi である本をスペースに積む．このとき，スペースに積まれている本の書名は上から順に ioi ，joig ，joi となる．
  4. 書名が ioi である本を読んで返却する．このとき，スペースに積まれている本の書名は上から順に joig ，joi となる．
  5. 書名が egoi である本をスペースに積む．このとき，スペースに積まれている本の書名は上から順に egoi ，joig ，joi となる．
  6. 書名が egoi である本を読んで返却する．このとき，スペースに積まれている本の書名は上から順に joig ，joi となる．
  7. 書名が joig である本を読んで返却する．このとき，スペースに積まれている本の書名は joi となる．

よってビ太郎が読んだ本の書名 ioi ，egoi ，joig を順に改行区切りで出力する．

この入力例はすべての小課題の制約を満たす．

入力例 2

20
one
READ
two
three
four
five
six
seven
READ
eight
nine
READ
ten
eleven
READ
READ
twelve
READ
READ
READ

出力例 2

one
seven
nine
eleven
ten
twelve
eight
six

この入力例はすべての小課題の制約を満たす．
B - カーペット (Carpet)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

オシャレ好きのビ太郎は，カーペットを新調した．カーペットは縦 H 行，横 W 列のマス目状に区切られた長方形の形をしており，各マスは白か黒のいずれかの色で塗られている．カーペットの上から i 行目，左から j 列目 (1 \leqq i \leqq H，1 \leqq j \leqq W) にあるマスの色は，文字列 S_{i} の j 文字目が . のとき白色，# のとき黒色である．

ビ太郎は，カーペットの最も左上のマスに駒を置き，以下の操作を何回か行うことで，その駒をカーペットの最も右下のマスに到達させるという遊びを思いついた．

  • 駒が置かれているマスと色が異なり，かつ上下左右に隣接するマスを 1 つ選び，そのマスに駒を移動させる．

ビ太郎は，到達までの操作回数をなるべく少なくしたい．ただし，カーペットの模様によっては到達させられないかもしれない．

カーペットの模様の情報が与えられたとき，操作を繰り返すことで左上のマスから右下のマスに駒を到達させることが可能かを判定し，可能ならば操作回数の最小値を求めるプログラムを作成せよ．

制約

  • 1 \leqq H \leqq 500．
  • 1 \leqq W \leqq 500．
  • (H, W) \neq (1, 1)．
  • S_{i} は長さ W の文字列である (1 \leqq i \leqq H)．
  • S_{i} の 各文字は . または # である (1 \leqq i \leqq H)．
  • H, W は整数である．

小課題

  1. (4 点) H = 1．
  2. (14 点) H \leqq 5，W \leqq 5．
  3. (24 点) H \leqq 30，W \leqq 30．
  4. (58 点) 追加の制約はない．

採点に関する注意

すべての提出はジャッジシステム上で採点される．

提出されたソースコードは，小課題に対応するすべての採点用入力データについて正しい結果を返したとき，その小課題について正解と認められる．

各提出の得点は，提出されたソースコードについて正解と認められた小課題の得点の合計である．

この課題の得点は，この課題に対するすべての提出の得点の最大値である．

現在の得点は「提出結果」タブの「自分の得点状況」から確認できる．

入力

入力は以下の形式で標準入力から与えられる．

H W
S_{1}
S_{2}
\vdots
S_{H}

出力

操作を繰り返すことで左上のマスから右下のマスに駒を到達させることが可能な場合は操作回数の最小値を，不可能な場合は -1 を，標準出力に 1 行で出力せよ．

入力例 1

4 5
...#.
#####
...#.
#.###

出力例 1

9

例えば，図のような操作が考えられる．

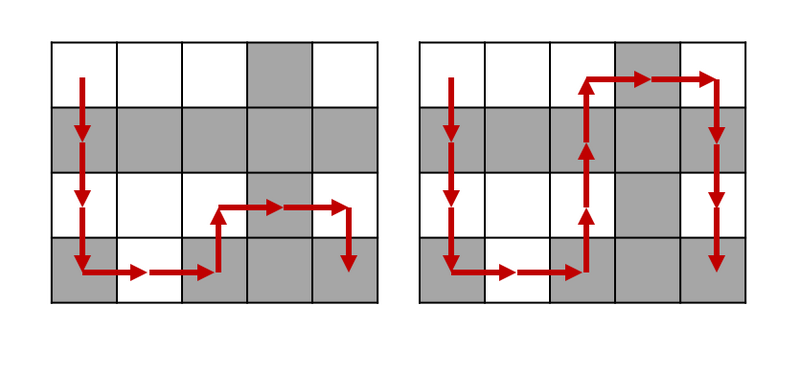
操作の 2 例の図示

左の例では 9 回の操作で，右の例では 13 回の操作で，左上のマスから右下のマスに駒を到達させることが可能である．

9 回よりも少ない操作回数で到達させることは不可能なので，9 を出力する．

この入力例は小課題 2, 3, 4 の制約を満たす．

入力例 2

3 3
...
...
...

出力例 2

-1

はじめから操作ができない場合もある．この場合，駒を右下のマスに到達させることは不可能なので，-1 を出力する．

この入力例は小課題 2, 3, 4 の制約を満たす．

入力例 3

1 5
.#.#.

出力例 3

4

この入力例はすべての小課題の制約を満たす．

入力例 4

5 5
###.#
.#...
.#..#
.####
##..#

出力例 4

12

この入力例は小課題 2, 3, 4 の制約を満たす．

入力例 5

7 5
.#.##
##...
.#.##
.###.
##.#.
...#.
##.#.

出力例 5

12

この入力例は小課題 3, 4 の制約を満たす．
C - 国土分割 (Land Division)

Time Limit: 1 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 国は縦 H 行，横 W 列のマス目状に区切られた長方形の形をしている．JOI 国の縦方向は南北方向に平行であり，横方向は東西方向に平行である．北から i 行目 (1 \leqq i \leqq H)，西から j 列目 (1 \leqq j \leqq W) のマスの人口は A_{i,j} 人である．

JOI 国では，行政の効率化のため，次の条件を満たす境界線を 1 本以上引くことで，国全体を 2 つ以上の地区に分割することにした．

  • 境界線はマス目の境界上にある．
  • 境界線は JOI 国の北端から南端または JOI 国の東端から西端を結ぶ線分である．

JOI 国の各マスの人口が与えられるので，考えられる分割方法のうち，すべての地区の人口が等しくなるような分割の方法は何通りあるかを求めるプログラムを作成せよ．

制約

  • 1 \leqq H \leqq 50．
  • 1 \leqq W \leqq 50．
  • 1 \leqq A_{i,j} \leqq 100\,000 (1 \leqq i \leqq H，1 \leqq j \leqq W)．
  • 入力される値はすべて整数である．

小課題

  1. (12 点) H = 1．
  2. (26 点) H \leqq 6，W \leqq 6．
  3. (62 点) 追加の制約はない．

採点に関する注意

すべての提出はジャッジシステム上で採点される．

提出されたソースコードは，小課題に対応するすべての採点用入力データについて正しい結果を返したとき，その小課題について正解と認められる．

各提出の得点は，提出されたソースコードについて正解と認められた小課題の得点の合計である．

この課題の得点は，この課題に対するすべての提出の得点の最大値である．

現在の得点は「提出結果」タブの「自分の得点状況」から確認できる．

入力

入力は以下の形式で標準入力から与えられる．

H W
A_{1,1} A_{1,2} \cdots A_{1,W}
A_{2,1} A_{2,2} \cdots A_{2,W}
\vdots
A_{H,1} A_{H,2} \cdots A_{H,W}

出力

標準出力に，すべての地区の人口が等しくなるような分割の方法は何通りあるかを 1 行で出力せよ．

入力例 1

2 3
10 10 20
10 10 20

出力例 1

3

下図のように，すべての地区の人口が等しくなるような分割の方法は 3 通りあるため，3 を出力する．

この入力例は小課題 2,3 の制約を満たす．

入力例 2

1 4
2 1 1 2

出力例 2

2

下図のように，すべての地区の人口が等しくなるような分割の方法は 2 通りあるため，2 を出力する．

この入力例はすべての小課題の制約を満たす．

入力例 3

3 3
2 9 4
7 5 3
6 1 8

出力例 3

2

下図のように，すべての地区の人口が等しくなるような分割の方法は 2 通りあるため，2 を出力する．

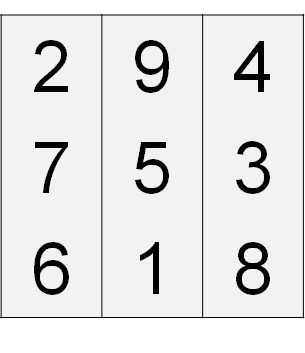
この入力例は小課題 2,3 の制約を満たす．

入力例 4

1 1
10000

出力例 4

0

すべての地区の人口が等しくなるような分割の方法は存在しないため，0 を出力する．

この入力例はすべての小課題の制約を満たす．
D - 飴 2 (Candies 2)

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

机の上に N 個の飴が横一列に並んでおり，左から順に 1 から N までの番号が付けられている．飴 i (1 \leqq i \leqq N) の美味しさは A_i である．

JOI 君は，N 個の飴のうちいくつかを選んで食べることにした．

ただし，飴を食べ過ぎないために，どの連続する K 個の飴についても，そのうち高々 2 個しか食べないようにする．すなわち，どの j (1 \leqq j \leqq N - K + 1) についても，飴 j から飴 j + K - 1 までの連続する K 個の飴のうち，食べる飴の個数は 2 個以下でなければならない．

このもとで，JOI 君は食べる飴の美味しさの合計をできるだけ大きくしたい．

N 個の飴の美味しさと K が与えられたとき，JOI 君が食べる飴の美味しさの合計の最大値を求めるプログラムを作成せよ．

制約

  • 2 \leqq K \leqq N \leqq 3\,000．
  • 1 \leqq A_i \leqq 10^9 (1 \leqq i \leqq N)．
  • 入力される値はすべて整数である．

小課題

  1. (4 点) N \leqq 20．
  2. (19 点) K \leqq 10．
  3. (47 点) N \leqq 300．
  4. (30 点) 追加の制約はない．

採点に関する注意

すべての提出はジャッジシステム上で採点される．

提出されたソースコードは，小課題に対応するすべての採点用入力データについて正しい結果を返したとき，その小課題について正解と認められる．

各提出の得点は，提出されたソースコードについて正解と認められた小課題の得点の合計である．

この課題の得点は，この課題に対するすべての提出の得点の最大値である．

現在の得点は「提出結果」タブの「自分の得点状況」から確認できる．

入力

入力は以下の形式で標準入力から与えられる．

N K
A_1 A_2 \cdots A_N

出力

標準出力に，JOI 君が食べる飴の美味しさの合計の最大値を 1 行で出力せよ．

入力例 1

5 4
1 3 2 4 3

出力例 1

8

JOI 君が飴 1 ，飴 4 ， 飴 5 を食べるとき，美味しさの合計は 8 となる．

どの連続する 4 個の飴についても食べる飴の個数が 2 個以下であるような食べ方のうち，美味しさの合計が 9 以上であるようなものは存在しないため， 8 を出力する．

この入力例はすべての小課題の制約を満たす．

入力例 2

6 3
3 7 1 5 6 4

出力例 2

21

JOI 君が飴 1 ，飴 2 ， 飴 4 ，飴 5 を食べるとき，美味しさの合計は 21 となる．

どの連続する 3 個の飴についても食べる飴の個数が 2 個以下であるような食べ方のうち，美味しさの合計が 22 以上であるようなものは存在しないため， 21 を出力する．

この入力例はすべての小課題の制約を満たす．

入力例 3

5 2
3 3 2 2 1

出力例 3

11

この入力例はすべての小課題の制約を満たす．

入力例 4

12 5
864814169 716638377 926889183 891468826 217138351 891972397 504371916 678159995 435478604 181254225 760822841 688502728

出力例 4

4427122428

この入力例はすべての小課題の制約を満たす．
E - 交易計画 (Trade Plan)

Time Limit: 4 sec / Memory Limit: 1024 MiB

配点： 100 点

問題文

JOI 合衆国には 1 から N までの番号が付けられた N 個の都市と，1 から M までの番号が付けられた M 本の道路がある．道路 i (1 \leqq i \leqq M) は，都市 U_i と都市 V_i を双方向に結んでいる．

JOI 合衆国は 1 から K までの番号が付けられた K 個の州からなる．都市 j (1 \leqq j \leqq N) は州 S_j に属している．また，どの州も少なくとも 1 つの都市を含む．

JOI 合衆国の産業大臣である K 理事長は，これから Q 回の交易を行いたいと考えている．k 番目の交易 (1 \leqq k \leqq Q) は，都市 A_k から都市 B_k にいくつかの道路や都市を通って特産品を輸送するというものである．ただし，この交易に協力してくれるのは州 S_{A_k} と 州 S_{B_k} のみ (S_{A_k} = S_{B_k} の場合は州 S_{A_k} のみ) であり，これらの州に属していない都市を通ると特産品は盗まれてしまう．

K 理事長は特産品が盗まれないように交易を行うような輸送経路があるのかを調べたい．都市と道路の配置，州と交易の情報が与えられたとき，各交易について特産品を無事届けることが可能かを判定するプログラムを作成せよ．

制約

  • 2 \leqq N \leqq 400\,000．
  • 1 \leqq M \leqq 400\,000．
  • 1 \leqq K \leqq N．
  • 1 \leqq U_i < V_i \leqq N (1 \leqq i \leqq M)．
  • (U_i, V_i) \neq (U_j, V_j) (1 \leqq i < j \leqq M)．
  • 1 \leqq S_j \leqq K (1 \leqq j \leqq N)．
  • すべての l (1 \leqq l \leqq K) について，S_j = l となる j (1 \leqq j \leqq N) が存在する．
  • 1 \leqq Q \leqq 400\,000．
  • 1 \leqq A_k \leqq N (1 \leqq k \leqq Q)．
  • 1 \leqq B_k \leqq N (1 \leqq k \leqq Q)．
  • A_k \neq B_k (1 \leqq k \leqq Q)．
  • 入力される値はすべて整数である．

小課題

  1. (5 点) N \leqq 1\,000，M \leqq 1\,000，Q \leqq 1\,000．
  2. (11 点) 州 l (1 \leqq l \leqq K) に属するすべての都市は，道路と州 l に属する都市のみを通って互いに行き来できる．
  3. (42 点) N \leqq 80\,000，M \leqq 80\,000，Q \leqq 80\,000．
  4. (42 点) 追加の制約はない．

採点に関する注意

すべての提出はジャッジシステム上で採点される．

提出されたソースコードは，小課題に対応するすべての採点用入力データについて正しい結果を返したとき，その小課題について正解と認められる．

各提出の得点は，提出されたソースコードについて正解と認められた小課題の得点の合計である．

この課題の得点は，この課題に対するすべての提出の得点の最大値である．

現在の得点は「提出結果」タブの「自分の得点状況」から確認できる．

入力

入力は以下の形式で標準入力から与えられる．

N M K
U_1 V_1
U_2 V_2
\vdots
U_M V_M
S_1 S_2 \cdots S_N
Q
A_1 B_1
A_2 B_2
\vdots
A_Q B_Q

出力

標準出力に Q 行で出力せよ．k 行目 (1 \leqq k \leqq Q) には，k 番目の交易において特産品を届けることが可能であれば 1 を，不可能であれば 0 を出力せよ．

入力例 1

4 3 2
1 2
2 3
3 4
1 2 1 2
3
1 2
1 3
1 4

出力例 1

1
0
1
  • 1 番目の交易は，州 1 または州 2 に属する都市のみを通って，都市 1 から都市 2 に特産品を輸送するというものである．都市 1 → 都市 2 と輸送すれば条件を満たすので，1 を出力する．
  • 2 番目の交易は，州 1 に属する都市のみを通って，都市 1 から都市 3 に特産品を輸送するというものである．条件を満たす輸送経路は存在しないので，0 を出力する．
  • 3 番目の交易は，州 1 または州 2 に属する都市のみを通って，都市 1 から都市 4 に特産品を輸送するというものである．都市 1 → 都市 2 → 都市 3 → 都市 4 と輸送すれば条件を満たすので，1 を出力する．

この入力例は小課題 1, 3, 4 の制約を満たす．

入力例 2

4 2 1
1 3
2 4
1 1 1 1
4
1 2
1 3
2 3
2 4

出力例 2

0
1
0
1

この入力例は小課題 1, 3, 4 の制約を満たす．

入力例 3

6 5 3
1 2
3 4
5 6
1 4
3 5
1 1 2 2 3 3
4
1 4
1 5
3 6
4 3

出力例 3

1
0
1
1

この入力例はすべての小課題の制約を満たす．

入力例 4

8 11 3
4 8
1 8
4 6
3 5
2 4
7 8
6 7
3 4
1 4
2 3
3 8
2 3 1 1 2 1 2 1
10
8 2
8 1
2 7
5 3
5 7
4 8
1 8
6 8
6 5
1 8

出力例 4

1
1
0
1
0
1
1
1
1
1

この入力例は小課題 1, 3, 4 の制約を満たす．