Time Limit: 1 sec / Memory Limit: 128 MiB
配点: 100 点
JOI (日本情報オリンピック) の本選に向けてプログラミングの練習をしていたあなたは,今年度の JOI の予選の問題には数値を扱う問題ばかりが出題され,文字列を扱う問題がなかったことに気がついた.そこであなたは,こっそり文字列の問題に強くなってライバルたちに差をつけることにした.
JOIの過去問を眺めていると,J,O,I の 3 種類の文字からなる文字列に慣れておく必要がありそうなことがわかった.そこで,そのような文字列について考えよう.あなたは「与えられた文字列が JOI という部分文字列をもつかどうかを答えよ」という問題を思いついたものの,これはすぐに解けてしまった.もっとレベルの高い問題を解きたいあなたは,以下のような問題を作った.
文字列 t が文字列 s の部分文字列であるとは,t の先頭および末尾に何文字か (0 文字でもよい) を付け足すと s になることである.たとえば,JJOOII は OJJOOIIOJOI の部分文字列である.一方,JOI は JOOI の部分文字列ではない.
また,0 以上の整数 k に対し,レベル k の JOI 列とは,k 個の文字 J,k 個の文字 O,k 個の文字 I をこの順に並べた文字列のことであるとする.たとえば,JJOOII はレベル 2 の JOI 列である.
与えられた文字列の部分文字列である JOI 列のうち,レベルが最大のものを求めたい.
課題
J,O,I の 3 種類の文字からなる長さ N の文字列 S が与えられたとき,レベル k の JOI 列が S の部分文字列であるような最大の k の値を求めるプログラムを作成せよ.
制限
| 1 \leqq N \leqq 1000000 \,(= 10^6) | S の長さ |
入力
標準入力から以下のデータを読み込め.
- 1 行目には
J,O,Iの 3 種類の文字からなる文字列 S が書かれている.
出力
標準出力に,レベル k の JOI 列が S の部分文字列であるような最大の k の値を表す整数を 1 行で出力せよ.
採点基準
採点用データのうち,配点の 20 %分については,N \leqq 100 を満たす.
入力例 1
OJJOOIIOJOI
出力例 1
2
OJJOOIIOJOI はレベル 2 の JOI 列である JJOOII を部分文字列として含んでおり,
レベル 3 以上の JOI 列は部分文字列として含まない.
入力例 2
IJJIIJJJ
出力例 2
0
レベル 0 の JOI 列は長さ 0 の文字列である.
入力例 3
JOIJOIJOIJOIJOI
出力例 3
1
入力例 4
OOJJJJJJJOOOOIIIII
出力例 4
4
Source Name
JOI 2011/2012 本選 問題1Time Limit: 1 sec / Memory Limit: 128 MiB
AtCoder からのお知らせ:この問題は、「1行目に A B の形式で与えられていないものが含まれている」という、テストケースの不備が報告されています。もし AC が取れない場合は、大会公式ページに公開されている採点用データをご確認ください。
配点: 100 点
1 から 1000 までのどれかの整数が書かれたカードがたくさんある.アンナとブルーノはそれらのカードを用いて,次のようなゲームをする.
アンナは A 枚,ブルーノは B 枚のカードからなる山を持つ.アンナは A 枚のカードの中から任意の何枚か (0 枚でもよい) を捨てて新しい山を作る.ブルーノは B 枚のカードからなる山の一番上から何枚か (0 枚でもよい) と,一番下から何枚か (0 枚でもよい) を捨てて新しい山を作る.ただし,捨てる際に残ったカードの並び替えは行わない.このように作った 2 つの山が一致していたら,一方の山に含まれるカードの枚数が 2 人の得点になる.ただし,2 つの山が一致するとは,山に含まれるカードの枚数 n が同じで,かつ上から i 番目 (1 \leqq i \leqq n) に書かれたカードの整数が全て同じであることである.
例えば,アンナが 5 枚のカードの山を持ち,書かれている整数は上から順に 1, 2, 3, 4, 5 であり,ブルーノが 4 枚のカードの山を持ち,書かれている整数が上から順に 3, 1, 4, 1 であったとする.このとき,アンナが 2, 3, 5 のカードを捨て,ブルーノが一番上の 3 と一番下の 1 のカードを捨てると 2 人の山が一致する.このとき,残った山の一方に含まれるカードの枚数は 2 枚なので, 2 人は得点 2 を得る.
2 人の得点の最大値を求めたい.
アンナ

ブルーノ

課題
アンナとブルーノが持っているカードの山の情報が与えられたときに,2 人の得点の最大値を求めるプログラムを作成せよ.
制限
| 1 \leqq A \leqq 5000 |
| 1 \leqq B \leqq 5000 |
| カードに書かれている整数は 1 以上 1000 以下である. |
入力
標準入力から以下のデータを読み込め.
1 行目には,整数 A, B が空白を区切りとして書かれている.
2 行目には,A 個の整数が空白を区切りとして書かれており,i 番目の整数 (1 \leqq i \leqq A) はアンナの持っている山の上から i 番目のカードに書かれている整数を表す.
3 行目には,B 個の整数が空白を区切りとして書かれており,j 番目の整数 (1 \leqq j \leqq B) はブルーノの持っている山の上から j 番目のカードに書かれている整数を表す.
出力
標準出力に,得点の最大値を表す整数を 1 行で出力せよ.
採点基準
採点用データのうち,配点の 10 %分については,A \leqq 10, B \leqq 10 を満たす.
採点用データのうち,配点の 50 %分については,A \leqq 100, B \leqq 100 を満たす.
入力例 1
5 4 1 2 3 4 5 3 1 4 1
出力例 1
2
この入出力例は問題文中の例に対応している.
入力例 2
6 5 4 1 5 2 3 4 4 5 4 2 3
出力例 2
3
この入出力例では,2 人が得点 3 を得る方法が 2 通り存在する.アンナが 1, 2, 3 のカードを捨てブルーノが 2, 3 のカードを捨てたとき,2 人の山は上から順に 4, 5, 4 となり,2 人の得点は 3 点となる.また,アンナが 1, 5, 4 のカードを捨てブルーノが一番上の 4 と 5 のカードを捨てたとき,2 人の山は上から順に 4, 2, 3 となり,2 人の得点は 3 点となる.
Source Name
JOI 2011/2012 本選 問題2Time Limit: 1 sec / Memory Limit: 128 MiB
配点: 100 点
太郎くんは,JOI 神社で開かれる夏祭りに行くことにした.
JOI 神社に向かう道に沿って,N 個の夜店が開かれている.それぞれの夜店には,1 から N までの番号が順番についており,遊んだ時の楽しさと遊ぶのにかかる時間がそれぞれ整数で決まっている.夜店 i で遊んだ時の楽しさは A_i で,夜店 i で遊ぶのにかかる時間は B_i である.
また,夏祭りのイベントとして花火大会があり,時刻 S に最も大きな花火が打ち上げられる.太郎くんはこの最も大きな花火を見たいと思っている.
太郎くんは夜店と花火の両方を楽しむために,夏祭りに到着する時刻 0 から夏祭りが終わる時刻 T までの予定を立てることにした.
太郎くんは夜店の中から k 個 (1 \leqq k \leqq N) の夜店を選び,それぞれに対して訪れる時刻を整数で決める.同じ夜店を 2 度選ぶことはできない.選ばれた夜店の番号を小さい順に y_1,y_2,\ldots,y_k とし,夜店 y_i を訪れる時刻を x_{y_i} とすると,太郎くんは夜店 y_i で時刻 x_{yi} から時刻 x_{y_i} + B_{y_i} まで遊ぶ.
太郎くんは夜店の番号の小さい順に遊び,同時に 2 つの夜店では遊べない.また,夜店と夜店の間の移動にかかる時間は無視できる.
時刻 T を超えると夏祭りが終わるので,夜店で遊ぶことはできない.また,夜店で遊んでいる間は花火を見ることはできない.ただし,時刻 S がある夜店で遊び始める時刻や遊び終わる時刻であった場合は,太郎くんは花火を見ることができるものとする.
すなわち,予定は以下の条件を満たしていなければならない.
- y_1 < y_2 < \ldots < y_k
- x_{y_1},x_{y_2},\ldots , x_{y_k} は整数.
- 0\leqq x_{y_1} < x_{y_1} + B_{y_1} \leqq x_{y_2} < x_{y_2} + B_{y_2} \leqq \ldots \leqq x_{y_k} < x_{y_k} + B_{y_k} \leqq T
- x_{y_i} < S < x_{y_i}+B_{y_i} となるような i は存在しない.
選ばれた夜店の楽しさ A_{y_1},A_{y_2},\ldots,A_{y_k} の合計をを M とする.太郎くんは M ができるだけ大きくなるように予定を立てたいと思っている.
課題
N 個の夜店の情報と時刻 S, T が与えられた時,M の最大値を求めるプログラムを作成せよ.
制限
| 1 \leqq N \leqq 3000 | 夜店の数 |
| 1 \leqq T \leqq 3000 | 夏祭りが終わる時刻 |
| 0 \leqq S \leqq T | 最も大きな花火が打ち上げられる時刻 |
| 0 \leqq A_i \leqq 100000 \,(= 10^5) | 夜店 i で遊んだ時の楽しさ |
| 0 \leqq B_i \leqq 3000 | 夜店 i で遊ぶのにかかる時間 |
入力
標準入力から以下の入力を読み込め.
入力の 1 行目には整数 N, T, S が空白を区切りとして書かれており,夜店の数が N 個,夏祭りが終わる時刻が T,最も大きな花火が打ち上げられる時刻が S であることを表す.
続く N 行には夜店の情報が書かれている.入力の i + 1 (1\leqq i \leqq N) 行目には整数 A_i, B_i が空白を区切りとして書かれており,夜店 i で遊んだ時の楽しさが A_i で,夜店 i で遊ぶのにかかる時間が B_i であることを表す.
また,すべての入力において,1 つ以上の予定を立てられることが保証されている.
出力
標準出力に,M の最大値を表す整数を 1 行で出力せよ.
採点基準
採点用データのうち,
配点の 10 %分については,N \leqq 20 を満たす.
配点の 20 %分については,S = 0 を満たす.
配点の 30 %分については,これら 2 つの条件の少なくとも一方を満たす.また,これら 2 つの条件の両方を満たすような採点用データはない.
入力例 1
5 20 14 8 9 2 4 7 13 6 3 5 8
出力例 1
16
この例において,
夜店 1 を時刻 0 に訪れ,
夜店 2 を時刻 9 に訪れ,
夜店 4 を時刻 14 に訪れるような予定を立てると,M を最も大きくすることができる.
このとき,M = 8 + 2 + 6 = 16 である.
Source Name
JOI 2011/2012 本選 問題3Time Limit: 2.5 sec / Memory Limit: 512 MiB
配点: 100 点
JOI くんは板に釘を刺して遊んでいる.下図のように,JOI くんは一辺 N 本の正三角形の形に釘を並べて刺した.上から a 行目 (1\leqq a\leqq N) には a 本の釘が並んでいる.そのうち左から b 本目 (1\leqq b\leqq a) の釘を (a, b) で表す.

釘を頂点とする正三角形が,「各辺が全体の正三角形の辺のいずれかと平行で,全体の正三角形と同じ向き」であるとき,この正三角形を「よい正三角形」と呼ぶ.すなわち,「よい正三角形」とは,3 本の釘 (a, b), (a + x, b), (a + x, b + x) を頂点とする正三角形のことである(ただし a, b, x は 1 \leqq a < N, 1 \leqq b \leqq a, 1 \leqq x \leqq N − a をみたす).
JOI くんは,輪ゴムを使って,「よい正三角形」の周りを囲うことにした.
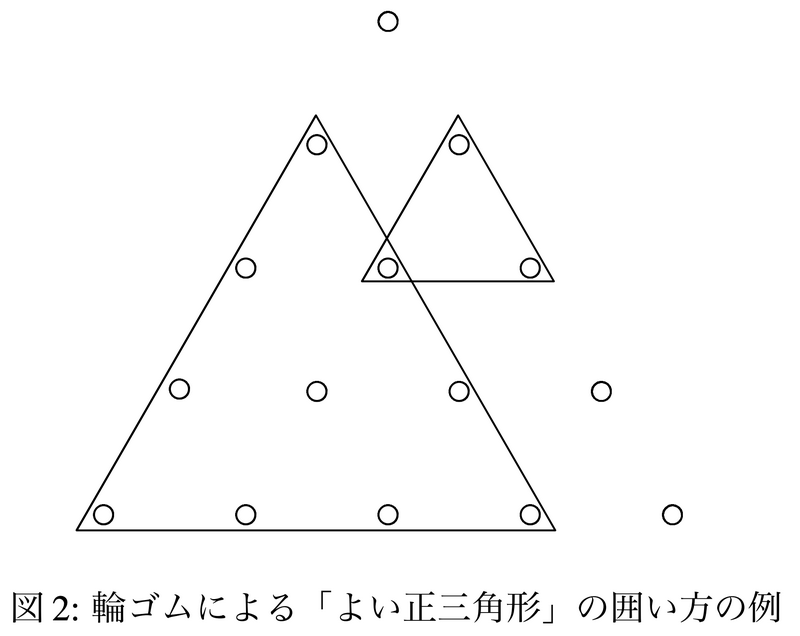
課題
正三角形の一辺に並んでいる釘の本数 N と,JOI くんが持っている輪ゴムの数 M と,M 本の輪ゴムによる「よい正三角形」の囲い方が与えられたとき,1 本以上の輪ゴムで囲われた釘の本数を求めるプログラムを作成せよ.
制限
| 2 \leqq N \leqq 5000 | 一辺に並んでいる釘の本数 |
| 1 \leqq M \leqq 500000 \,(= 5\times 10^5) | 輪ゴムの数 |
入力
標準入力から以下のデータを読み込め.
- 1 行目には整数 N, M が空白を区切りとして書かれている.N は正三角形の一辺に並んでいる釘の本数を,M は JOI くんの持っている輪ゴムの数をそれぞれ表す.
- 続く M 行は輪ゴムによる「よい正三角形」の囲い方の情報を表す.i + 1 行目 (1 \leqq i \leqq M) には整数 A_i,B_i,X_i (1\leqq A_i < N, 1\leqq B_i\leqq A_i , 1\leqq X_i \leqq N-A_i) が空白を区切りとして書かれている.これは,i 本目の輪ゴムは 3 本の釘 (A_i,B_i),(A_i+X_i,B_i),(A_i+X_i,B_i+X_i) を頂点とする「よい正三角形」を囲っていることを表す.
出力
標準出力に,1 本以上の輪ゴムに囲われている釘の本数を 1 行で出力せよ.
採点基準
採点用データのうち,配点の 30 %分については,M\leqq 10000 を満たす.
入力例 1
5 2 2 2 1 2 1 3
出力例 1
12
この例は図 2 のような「よい正三角形」の囲い方に対応している.この例において,(1, 1), (4, 4), (5, 5) 以外の 12 本の釘が 1 本以上の輪ゴムで囲われている.
Source Name
JOI 2011/2012 本選 問題4Time Limit: 2.5 sec / Memory Limit: 128 MiB
配点: 100 点
JOI 国には N 個の街があり,それらの間は M 本の双方向に通行可能な道路で結ばれている.国民は道路を通ってそれらの街を移動する.
JOI 国の国民には,お祭りが好きな人が多く,現在,K 個の街でお祭りが開催されており,非常に賑わっている.一方で,一部の国民はお祭りを騒がしいとして嫌い,お祭りにできるだけ近づきたくないと思っている.
そこで国王は,優秀なプログラマーであるあなたに,そのようなお祭りを嫌う国民のため,ある街からある街に移動するために,お祭りが開催されている街にどれだけ近づかずに移動することができるかを高速に調べることのできるプログラムの作成を依頼した.
課題
道路の情報とお祭りが開催されている街の情報,および Q 個のクエリ(出発する街 S_i と行きたい街 T_i の組)が与えられる.各クエリ i に対し,街 S_i から街 T_i へのすべての経路のうち,お祭りまでの距離が最大となる経路の,お祭りまでの距離を求めるプログラムを作成せよ.ただし,ある経路のお祭りまでの距離とは,経路上の街からお祭りが開催されている街までの移動距離の最小値のことである.
制限
| 2 \leqq N \leqq 100000 \,(= 10^5) | JOI 国の街の個数 |
| 1 \leqq N \leqq 200000 \,(= 2\times 10^5) | JOI 国の道路の本数 |
| 1 \leqq K \leqq N | お祭りが開催されている街の個数 |
| 1 \leqq Q \leqq 100000 \,(= 10^5) | クエリの個数 |
| 1 \leqq L_i \leqq 1000 | i 番目の道路の長さ |
入力
標準入力から以下のデータを読み込め.
- 1 行目には整数 N, M, K, Q が空白を区切りとして書かれている.N は JOI 国の街の個数を,M は JOI 国の道路の本数を,K はお祭りが開催されている街の個数を,Q はクエリの個数をそれぞれ表す.街には 1,2,\ldots,N の番号がつけられている.
- 続く M 行は道路の情報を表す.i + 1 行目 (1\leqq i\leqq M) には整数 A_i,B_i,L_i (1\leqq A_i\leqq N,1\leqq B_i\leqq N) が空白を区切りとして書かれている.これは,i 番目の道路が街 A_i と街 B_i を結んでおり,長さが L_i であることを表す.道路の両端が同じ街であることはない.また,任意の 2 つの街 p, q に対し,p と q を結ぶ道路は 2 本以上存在しない.どの街からどの街へもいくつかの道路をたどって行くことができる.
- 続く K 行はお祭りが開催されている街の情報を表す.i + M + 1 行目 (1\leqq i\leqq K) には 1 つの整数 F_i (1\leqq F_i\leqq N) が書かれている.これは街 F_i でお祭りが開催されていることを表す.F_1,\ldots,F_K の中に同じ値が 2 回以上現れることはない.
- 続く Q 行はクエリを表す.i + M + K + 1 行目 (1\leqq i\leqq Q) には 2 つの整数 S_i,T_i (1\leqq S_i\leqq N,1\leqq T_i\leqq N, S_i\neq T_i) が空白を区切りとして書かれている.これは i 番目のクエリの出発する街が S_i であり行きたい街が T_i であることを表す.
出力
標準出力に,全クエリへの答えを Q 行で出力せよ.すなわち,i 行目に,街 S_i から街 T_i へのすべての経路のうち,お祭りまでの距離が最大となる経路の,お祭りまでの距離を表す整数を出力せよ.
採点基準
採点用データのうち,
配点の 10 %分については,Q=1 を満たす.
配点の 20 %分については,N\leqq 5000,Q\leqq 5000 を満たす.
配点の 30 %分については,これら 2 つの条件の少なくとも一方を満たす.また,これら 2 つの条件の両方を満たすような採点用データはない.
入力例 1
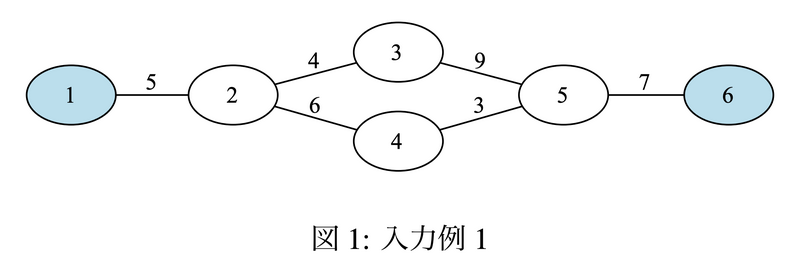
6 6 2 3 1 2 5 2 3 4 2 4 6 3 5 9 4 5 3 5 6 7 1 6 3 4 5 2 1 4
出力例 1
7 5 0
6 つの街が 6 本の道路で結ばれており,お祭りは街 1, 6 の 2 つの街で開催されている.クエリは以下の 3 つである.
- 1 つ目のクエリは街 3 から街 4 へ行くというものである.街 2 を経由する経路ではお祭りまでの距離は 5,街 5 を経由する経路ではお祭りまでの距離は 7 となるため,答えは 7 である.
- 2 つ目のクエリは街 5 から街 2 へ行くというものである.街 3 と街 4 のどちらを経由しても,街 2 でお祭りまでの距離が最小となり,答えは 5 である.
- 3 つ目のクエリは街 1 から街 4 へ行くというものである.街 1 はお祭りが開催されている街であるため,答えは 0 となる.